Moran M.J., Shapiro H.N. Fundamentals of Engineering Thermodynamics
Подождите немного. Документ загружается.

526 Chapter 11 Thermodynamic Relations
enthalpy departure
EXAMPLE 11.8 Using the Generalized Enthalpy Departure Chart
Nitrogen enters a turbine operating at steady state at 100 bar and 300 K and exits at 40 bar and 245 K. Using the enthalpy
departure chart, determine the work developed, in kJ per kg of nitrogen flowing, if heat transfer with the surroundings can be
ignored. Changes in kinetic and potential energy from inlet to exit also can be neglected.
SOLUTION
Known: A turbine operating at steady state has nitrogen entering at 100 bar and 300 K and exiting at 40 bar and 245 K.
Find: Using the enthalpy departure chart, determine the work developed.
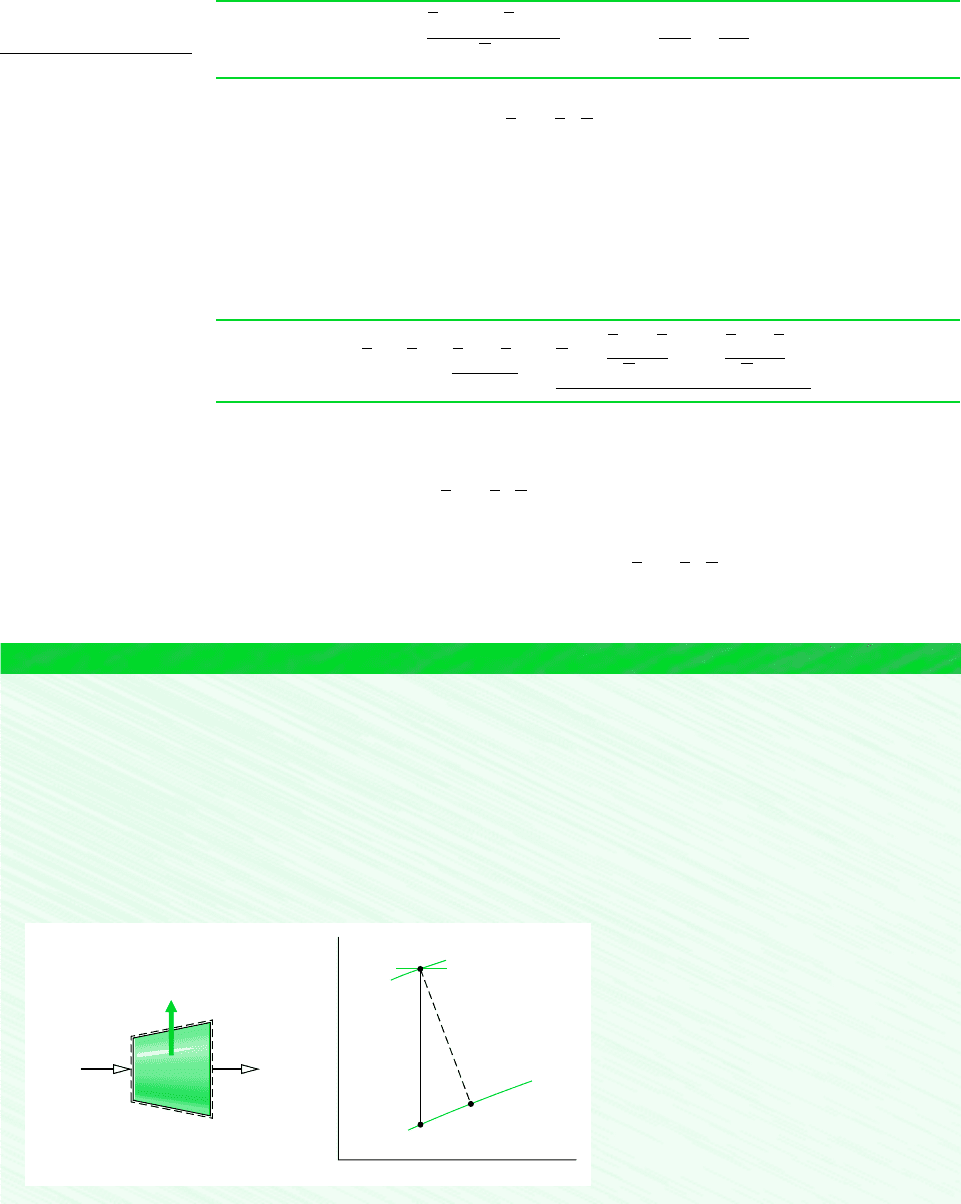
Schematic and Given Data:
1
2
2s
T
s
12
N
2
p
1
= 100 bar
T
1
= 300 K
p
2
= 40 bar
T
2
= 245 K
W
cv
–––
m
·
·
Figure E11.8
Or, on a per mole basis, the enthalpy departure is
(11.84)
The right side of Eq. 11.84 depends only on the reduced temperature T
R
and reduced pres-
sure p
R
. Accordingly, the quantity ( ) the enthalpy departure, is a function only
of these two reduced properties. Using a generalized equation of state giving Z as a function
of T
R
and p
R
, the enthalpy departure can readily be evaluated with a computer. Tabular rep-
resentations are also found in the literature. Alternatively, the graphical representation pro-
vided in Fig. A-4 can be employed.
EVALUATING ENTHALPY CHANGE. The change in specific enthalpy between two states
can be evaluated by expressing Eq. 11.80 in terms of the enthalpy departure as
(11.85)
The first underlined term in Eq. 11.85 represents the change in specific enthalpy between the
two states assuming ideal gas behavior. The second underlined term is the correction that must
be applied to the ideal gas value for the enthalpy change to obtain the actual value for the en-
thalpy change. The quantity ( ) at state 1 would be calculated with an equation giving
Z(T
R
, p
R
) or obtained from tables or the generalized enthalpy departure chart, Fig. A-4, using
the reduced temperature T
R1
and reduced pressure p
R1
corresponding to the temperature T
1
and
pressure p
1
at the initial state, respectively. Similarly, ( ) at state 2 would be evaluated
using T
R2
and p
R2
. The use of Eq. 11.85 is illustrated in the next example.
RT
c
h* h
RT
c
h* h
h
2
h
1
h
2
*
h
1
*
RT
c
ca
h* h
RT
c
b
2
a
h* h
RT
c
b
1
d
RT
c
,h* h
h*1T 2 h1T, p2
RT
c
T
2
R
p
R
0
a
0Z
0T
R
b
p
R
dp
R
p
R

11.7 Generalized Charts for Enthalpy and Entropy 527
Assumptions:
1. The control volume shown on the accompanying figure operates at steady state.
2. There is no significant heat transfer between the control volume and its surroundings.
3. Changes in kinetic and potential energy between inlet and exit can be neglected.
4. Equilibrium property relations apply at the inlet and exit.
Analysis: The mass and energy rate balances reduce at steady state to give
where is the mass flow rate. Dropping the heat transfer term by assumption 2 and the kinetic and potential energy terms
by assumption 3 gives on rearrangement
The term h
1
h
2
can be evaluated as follows:
In this expression, M is the molecular weight of nitrogen and the other terms have the same significance as in Eq. 11.85.
With specific enthalpy values from Table A-23 at T
1
300 K and T
2
245 K, respectively
The terms ( ) at states 1 and 2 required by the above expression for h
1
h
2
can be determined from Fig. A-4.
First, the reduced temperature and reduced pressure at the inlet and exit must be determined. From Tables A-1, T
c
126 K,
p
c
33.9 bar. Thus, at the inlet
At the exit
By inspection of Fig. A-4
Substituting values
Due to inaccuracy in reading values from a graph such as Fig. A-4, we cannot expect extreme accuracy in the final cal-
culated result.
If the ideal gas model were used, the work would be determined as 1602 kJ/kmol, or 57.2 kJ/kg. These values are over
14% greater than the respective values determined by including the enthalpy departure.
W
#
cv
m
#
1
28
kg
kmol
c1602
kJ
kmol
a8.314
kJ
kmol
#
K
b
1126 K2 10.5 0.312d 50.1 kJ/kg
a
h
* h
RT
c
b
1
0.5,
a
h* h
RT
c
b
2
0.31
T
R2
245
126
1.94,
p
R2
40
33.9
1.18
T
R1
300
126
2.38,
p
R1
100
33.9
2.95
RT
c
h* h
h
1
*
h
2
*
8723 7121 1602 kJ/kmol
h
1
h
2
1
M
eh
1
*
h
2
*
R
T
c
ca
h* h
RT
c
b
1
a
h* h
RT
c
b
2
df
W
#
cv
m
#
h
1
h
2
m
#
0
Q
#
cv
m
#
W
#
cv
m
#
ch
1
h
2
V
1
2
V
2
2
2
g1z
1
z
2
2d
❶
❷
❶
❷

GENERALIZED ENTROPY DEPARTURE CHART
A generalized chart that allows changes in specific entropy to be evaluated can be developed
in a similar manner to the generalized enthalpy departure chart introduced above. The dif-
ference in specific entropy between states 1 and 2 of a gas (or liquid) can be expressed as
the identity
(11.86)
where [s(T, p) s*(T, p)] denotes the specific entropy of the substance relative to that of its
ideal gas model when both are at the same temperature and pressure. Equation 11.86 indi-
cates that the change in specific entropy between the two states equals the entropy change
determined using the ideal gas model plus a correction (shown underlined) that accounts for
the departure from ideal gas behavior. The ideal gas term can be evaluated using methods
introduced in Sec. 6.3.2. Let us consider next how the correction term is evaluated in terms
of the entropy departure.
DEVELOPING THE ENTROPY DEPARTURE. The following Maxwell relation gives the vari-
ation of entropy with pressure at fixed temperature:
(11.35)
Integrating from pressure p to pressure p at fixed temperature T gives
(11.87)
For an ideal gas, v RTp, so ( v T )
p
Rp. Using this in Eq. 11.87, the change in
specific entropy assuming ideal gas behavior is
(11.88)
Subtracting Eq. 11.88 from Eq. 11.87 gives
(11.89)
Since the properties of a substance tend to merge into those of its ideal gas model as pres-
sure tends to zero at fixed temperature, we have
Thus, in the limit as p tends to zero, Eq. 11.89 becomes
(11.90)
Using p–v–T data only, Eq. 11.90 can be evaluated at states 1 and 2 and thus the correction
term of Eq. 11.86 evaluated.
Equation 11.90 can be expressed in terms of the compressibility factor Z and the reduced
properties T
R
and p
R
. The result, on a per mole basis, is the entropy departure
(11.91)
s*1T, p2 s 1T, p2
R
h
*1T 2 h1T, p2
RT
R
T
c
p
R
0
1Z 12
dp
R
p
R
s1T, p2 s*1T, p2
p
0
c
R
p
a
0v
0T
b
p
d dp
lim
p¿S0
3s1T, p¿ 2 s*1T, p¿24 0
3s1T, p2 s*1T, p24 3s1T, p¿2 s*1T, p¿ 24
p
p¿
c
R
p
a
0v
0T
b
p
d dp
s*1T, p2 s*1T, p¿ 2
p
p¿
R
p
dp
00
s1T, p2 s1T, p¿ 2
p
p¿
a
0v
0T
b
p
dp
a
0s
0p
b
T
a
0v
0T
b
p
53s1T
2
, p
2
2 s*1T
2
, p
2
24 3s1T
1
, p
1
2 s*1T
1
, p
1
246
s1T
2
, p
2
2 s1T
1
, p
1
2 s*1T
2
, p
2
2 s*1T
1
, p
1
2
528 Chapter 11 Thermodynamic Relations
entropy departure

11.7 Generalized Charts for Enthalpy and Entropy 529
The right side of Eq. 11.91 depends only on the reduced temperature T
R
and reduced pres-
sure p
R
. Accordingly, the quantity ( ) the entropy departure, is a function only of
these two reduced properties. As for the enthalpy departure, the entropy departure can be
evaluated with a computer using a generalized equation of state giving Z as a function of T
R
and p
R
. Alternatively, tabular data from the literature or the graphical representation provided
in Fig. A-5 can be employed.
EVALUATING ENTROPY CHANGE. The change in specific entropy between two states can
be evaluated by expressing Eq. 11.86 in terms of the entropy departure as
(11.92)
The first underlined term in Eq. 11.92 represents the change in specific entropy between the
two states assuming ideal gas behavior. The second underlined term is the correction that must
be applied to the ideal gas value for entropy change to obtain the actual value for the entropy
change. The quantity ( )
1
appearing in Eq. 11.92 would be calculated with an equa-
tion giving Z(T
R
, p
R
) or obtained from the generalized entropy departure chart, Fig. A-5, using
the reduced temperature T
R1
and reduced pressure p
R1
corresponding to the temperature T
1
and
pressure p
1
at the initial state, respectively. Similarly, ( )
2
would be evaluated using
T
R2
and p
R2
. The use of Eq. 11.92 is illustrated in the next example.
R,s* s
R,s* s
s
2
s
1
s
2
*
s
1
*
R ca
s
*
s
R
b
2
a
s
*
s
R
b
1
d
R,s* s
EXAMPLE 11.9 Using the Generalized Entropy Departure Chart
For the case of Example 11.8, determine (a) the rate of entropy production, in and (b) the isentropic turbine
efficiency.
SOLUTION
Known: A turbine operating at steady state has nitrogen entering at 100 bar and 300 K and exiting at 40 bar and 245 K.
Find: Determine the rate of entropy production, in and the isentropic turbine efficiency.
Schematic and Given Data: See Fig. E11.8.
Assumptions: See Example 11.8.
Analysis:
(a) At steady state, the control volume form of the entropy rate equation reduces to give
The change in specific entropy required by this expression can be written as
where M is the molecular weight of nitrogen and the other terms have the same significance as in Eq. 11.92.
The change in specific entropy can be evaluated using
s
2
*
s
1
*
s
°1T
2
2 s°1T
1
2 R ln
p
2
p
1
s
2
*
s
1
*
s
2
s
1
1
M
es
2
*
s
1
*
R
ca
s* s
R
b
2
a
s* s
R
b
1
df
s
#
cv
m
#
s
2
s
1
kJ/kg
#
K,
kJ/kg
#
K,

530 Chapter 11 Thermodynamic Relations
With values from Table A-23
The terms ( ) at the inlet and exit can be determined from Fig. A-5. Using the reduced temperature and reduced
pressure values calculated in the solution to Example 11.8, inspection of Fig. A-5 gives
Substituting values
(b) The isentropic turbine efficiency is defined in Sec. 6.8 as
where the denominator is the work that would be developed by the turbine if the nitrogen expanded isentropically from the
specified inlet state to the specified exit pressure. Thus, it is necessary to fix the state, call it 2s, at the turbine exit for an ex-
pansion in which there is no change in specific entropy from inlet to exit. With ( ) 0 and procedures similar to those
used in part (a)
Using values from part (a), the last equation becomes
or
The temperature T
2s
can be determined in an iterative procedure using data from Table A-23 and from
Fig. A-5 as follows: First, a value for the temperature T
2s
is assumed. The corresponding value of can then be obtained
from Table A-23. The reduced temperature (T
R
)
2s
T
2s
T
c
, together with p
R2
1.18, allows a value for to be
obtained from Fig. A-5. The procedure continues until agreement with the value on the right side of the above equation is
obtained. Using this procedure, T
2s
is found to be closely 228 K.
With the temperature T
2s
known, the work that would be developed by the turbine if the nitrogen expanded isentropically
from the specified inlet state to the specified exit pressure can be evaluated from
From Table A-23, From Fig. A-4 at p
R2
1.18 and (T
R
)
2s
228126 1.81
a
h
* h
RT
c
b
2s
0.36
h
2s
*
6654 kJ/kmol.
1
M
e 1h
1
*
h
2s
*
2 R
T
c
c a
h
* h
RT
c
b
1
a
h
* h
RT
c
b
2s
df
a
W
#
cv
m
#
b
s
h
1
h
2s
1s* s2
R
s°
1s
* s2
Rs°
s
°1T
2s
2 R a
s
* s
R
b
2s
182.3
0 s
°1T
2s
2 191.682 8.314 ln
40
100
R
a
s
* s
R
b
2s
1.746
0 cs
°1T
2s
2 s°1T
1
2 R ln a
p
2
p
1
b d R c a
s* s
R
b
2s
a
s* s
R
b
1
d
0 s
2s
*
s
1
*
R
c a
s
* s
R
b
2s
a
s
* s
R
b
1
d
s
2s
s
1
h
t
1W
#
cv
m
#
2
1W
#
cv
m
#
2
s
0.082
kJ
kg
#
K
s
#
cv
m
#
1
128 kg/ kmol2
c1.711
kJ
kmol
#
K
8.314
kJ
kmol
#
K
10.14 0.212d
a
s
* s
R
b
1
0.21,
a
s* s
R
b
2
0.14
Rs* s
s
2
*
s
1
*
185.775 191.682 8.314 ln
40
100
1.711
kJ
kmol
#
K

11.8 p–v–T Relations for Gas Mixtures 531
Values for the other terms in the expression for are obtained in the solution to Example 11.8. Finally
With the work value from Example 11.8, the turbine efficiency is
We cannot expect extreme accuracy when reading data from a generalized chart such as Fig. A-5, which affects the final
calculated result.
h
t
1W
#
cv
m
#
2
1W
#
cv
m
#
2
s
50.1
68.66
0.73
173% 2
a
W
#
cv
m
#
b
s
1
28
38723 6654 18.31421126210.5 0.3624 68.66 kJ/kg
1W
#
cv
m
#
2
s
❶
❶
11.8 p–v–T Relations for Gas Mixtures
Many systems of interest involve mixtures of two or more components. The principles of
thermodynamics introduced thus far are applicable to systems involving mixtures, but to ap-
ply them requires that the properties of mixtures be evaluated. Since an unlimited variety
of mixtures can be formed from a given set of pure components by varying the relative
amounts present, the properties of mixtures are available in tabular, graphical, or equation
forms only in particular cases such as air. Generally, special means are required for deter-
mining the properties of mixtures. In this section, methods for evaluating the p–v–T rela-
tions for pure components introduced in previous sections of the book are adapted to ob-
tain plausible estimates for gas mixtures. In Sec. 11.9 some general aspects of property
evaluation for multicomponent systems are introduced. The case of ideal gas mixtures is
taken up in Chap. 12.
To evaluate the properties of a mixture requires knowledge of the composition. The com-
position can be described by giving the number of moles (kmol or lbmol) of each compo-
nent present. The total number of moles, n, is the sum of the number of moles of each of
the components
(11.93)
The relative amounts of the components present can be described in terms of mole fractions.
The mole fraction y
i
of component i is defined as
(11.94)
Dividing each term of Eq. 11.93 by the total number of moles and using Eq. 11.94
(11.95)
That is, the sum of the mole fractions of all components present is equal to unity.
Most techniques for estimating mixture properties are empirical in character and are not
derived from fundamental principles. The realm of validity of any particular technique can
be established only by comparing predicted property values with empirical data. The brief
discussion to follow is intended only to show how certain of the procedures for evaluating
the p–v–T relations of pure components introduced previously can be extended to gas
mixtures.
1
a
j
i1
y
i
y
i
n
i
n
n n
1
n
2
###
n
j
a
j
i1
n
i

MIXTURE EQUATION OF STATE. One way the p–v–T relation for a gas mixture can be
estimated is by applying to the overall mixture an equation of state such as introduced in
Sec. 11.1. The constants appearing in the equation selected would be mixture values
determined with empirical combining rules developed for the equation. For example, mixture
values of the constants a and b for use in the van der Waals and Redlich–Kwong equations
would be obtained using relations of the form
(11.96)
where a
i
and b
i
are the values of the constants for component i and y
i
is the mole fraction.
Combination rules for obtaining mixture values for the constants in other equations of state
also have been suggested.
KAY’S RULE. The principle of corresponding states method for single components intro-
duced in Sec. 3.4 can be extended to mixtures by regarding the mixture as if it were a single
pure component having critical properties calculated by one of several mixture rules. Perhaps
the simplest of these, requiring only the determination of a mole fraction averaged critical
temperature T
c
and critical pressure p
c
, is Kay’s rule
(11.97)
where T
c,i
, p
c,i
, and y
i
are the critical temperature, critical pressure, and mole fraction of com-
ponent i, respectively. Using T
c
and p
c
, the mixture compressibility factor Z is obtained as
for a single pure component. The unknown quantity from among the pressure p, volume V,
temperature T, and total number of moles n of the gas mixture can then be obtained by solving
(11.98)
Mixture values for T
c
and p
c
also can be used to enter the generalized enthalpy departure and
entropy departure charts introduced in Sec. 11.7.
ADDITIVE PRESSURE RULE. Additional means for estimating p–v–T relations for mixtures
are provided by empirical mixture rules, of which several are found in the engineering liter-
ature. Among these are the additive pressure and additive volume rules. According to the
additive pressure rule, the pressure of a gas mixture occupying volume V at temperature T
is expressible as a sum of pressures exerted by the individual components
(11.99a)
where the pressures p
1
, p
2
, etc. are evaluated by considering the respective components to be
at the volume and temperature of the mixture. These pressures would be determined using
tabular or graphical p–v–T data or a suitable equation of state.
An alternative expression of the additive pressure rule in terms of compressibility factors
can be obtained. Since component i is considered to be at the volume and temperature of the
mixture, the compressibility factor Z
i
for this component is so the pressure
p
i
is
p
i
Z
i
n
i
RT
V
Z
i
p
i
V
n
i
RT,
p p
1
p
2
p
3
###
4
T,V
Z
pV
nRT
T
c
a
j
i1
y
i
T
c,i
,
p
c
a
j
i1
y
i
p
c,i
a a
a
j
i1
y
i
a
1
2
i
b
2
,
b a
a
j
i1
y
i
b
i
b
532 Chapter 11 Thermodynamic Relations
Kay’s rule
additive pressure rule

11.8 p–v–T Relations for Gas Mixtures 533
Similarly, for the mixture
Substituting these expressions into Eq. 11.99a and reducing gives the following relationship
between the compressibility factors for the mixture Z and the mixture components Z
i
(11.99b)
The compressibility factors Z
i
are determined assuming that component i occupies the entire
volume of the mixture at the temperature T.
ADDITIVE VOLUME RULE. The underlying assumption of the additive volume rule is that
the volume V of a gas mixture at temperature T and pressure p is expressible as the sum of
volumes occupied by the individual components
(11.100a)
where the volumes V
1
, V
2
, etc. are evaluated by considering the respective components to be
at the pressure and temperature of the mixture. These volumes would be determined from
tabular or graphical p–v–T data or a suitable equation of state.
An alternative expression of the additive volume rule in terms of compressibility factors can
be obtained. Since component i is considered to be at the pressure and temperature of the mix-
ture, the compressibility factor Z
i
for this component is so the volume V
i
is
Similarly, for the mixture
Substituting these expressions into Eq. 11.100a and reducing gives
(11.100b)
The compressibility factors Z
i
are determined assuming that component i exists at the
temperature T and pressure p of the mixture.
The next example illustrates alternative means for estimating the pressure of a gas mixture.
Z
a
j
i1
y
i
Z
i
4
p,T
V
ZnRT
p
V
i
Z
i
n
i
RT
p
Z
i
pV
i
n
i
RT,
V V
1
V
2
V
3
###
4
p,T
Z
a
j
i1
y
i
Z
i
4
T,V
p
ZnRT
V
EXAMPLE 11.10 Estimating Mixture Pressure by Alternative Means
A mixture consisting of 0.18 kmol of methane (CH
4
) and 0.274 kmol of butane (C
4
H
10
) occupies a volume of 0.241 m
3
at a
temperature of 238C. The experimental value for the pressure is 68.9 bar. Calculate the pressure, in bar, exerted by the mix-
ture by using (a) the ideal gas equation of state, (b) Kay’s rule together with the generalized compressibility chart, (c) the van
der Waals equation, and (d) the rule of additive pressures employing the generalized compressibility chart. Compare the cal-
culated values with the known experimental value.
additive volume rule
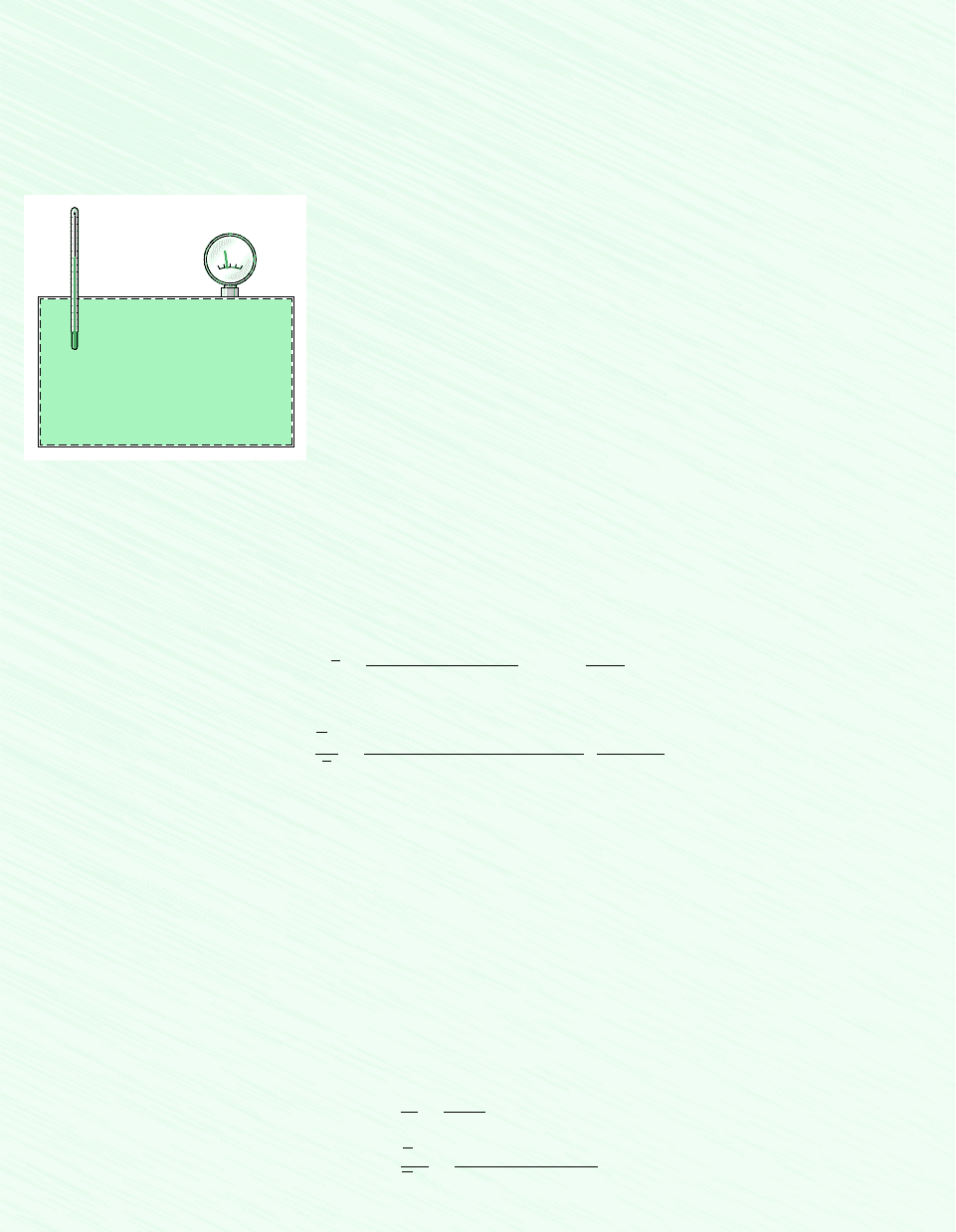
534 Chapter 11 Thermodynamic Relations
SOLUTION
Known: A mixture of two specified hydrocarbons with known molar amounts occupies a known volume at a specified
temperature.
Find: Determine the pressure, in bar, using four alternative methods, and compare the results with the experimental value.
Schematic and Given Data:
p = ?
T = 238°C
0.18 kmol CH
4
0.274 kmol C
4
H
10
V = 0.241 m
3
Figure E.11.10
Assumption: As shown in the accompanying figure, the system is the mixture.
Analysis: The total number of moles of mixture n is
Thus, the mole fractions of the methane and butane are, respectively
The specific volume of the mixture on a molar basis is
(a) Substituting values into the ideal gas equation of state
(b) To apply Kay’s rule, the critical temperature and pressure for each component are required. From Table A-1, for methane
and for butane
Thus, with Eqs. 11.97
Treating the mixture as a pure component having the above values for the critical temperature and pressure, the following
reduced properties are determined for the mixture:
0.794
v¿
R
v
p
c
RT
c
10.5312
141.332010
5
0
183142 1332.32
T
R
T
T
c
511
332.3
1.54
p
c
y
1
p
c1
y
2
p
c2
10.3962 146.42 10.6042 138.02 41.33 bar
T
c
y
1
T
c1
y
2
T
c2
10.3962 11912 10.6042 14252 332.3 K
T
c2
425 K,
p
c2
38.0 bar
T
c1
191 K,
p
c1
46.4 bar
80.01 bar
p
R
T
v
18314 N
#
m/ kmol
#
K21511 K2
10.531 m
3
/kmol2
`
1 bar
10
5
N/m
2
`
v
0.241 m
3
10.18 0.2742 kmol
0.531
m
3
kmol
y
1
0.396
and
y
2
0.604
n 0.18 0.274 0.454 kmol

11.8 p–v–T Relations for Gas Mixtures 535
Turning to Fig. A-2, Z 0.88. The mixture pressure is then found from
(c) Mixture values for the van der Waals constants can be obtained using Eqs. 11.96. This requires values of the van der Waals
constants for each of the two mixture components. Table A-24 gives the following values for methane:
Similarly, from Table A-24 for butane
Then, the first of Eqs. 11.96 gives a mixture value for the constant a as
Substituting into the second of Eqs. 11.96 gives a mixture value for the constant b
Inserting the mixture values for a and b into the van der Waals equation together with known data
(d) To apply the additive pressure rule with the generalized compressibility chart requires that the compressibility factor for
each component be determined assuming that the component occupies the entire volume at the mixture temperature. With this
assumption, the following reduced properties are obtained for methane
With these reduced properties, Fig. A-2 gives
Similarly, for butane
From Fig. A-2, Z
2
0.8.
The compressibility factor for the mixture determined from Eq. 11.99b is
Accordingly, the same value for pressure as determined in part (b) using Kay’s rule results: p 70.4 bar.
Z y
1
Z
1
y
2
Z
2
10.3962 11.02 10.6042 10.82 0.88.
v¿
R2
v
2
p
c2
RT
c2
10.882
1382010
5
0
183142 14252
0.95
T
R2
T
T
c2
511
425
1.2
Z
1
1.0.
v¿
R1
v
1
p
c1
RT
c1
10.241 m
3
0.18 kmol2 146.4 bar2
18314 N
#
m/kmol
#
K2 1191 K2
`
10
5
N/m
2
1 bar
` 3.91
T
R1
T
T
c1
511
191
2.69
66.91 bar
18314 N
#
m/kmol
#
K2
1511 K2
10.531 0.0872 1m
3
/kmol2
`
1 bar
10
5
N/m
2
`
8.113 bar
1m
3
/kmol2
2
10.531 m
3
/kmol2
2
p
RT
v b
a
v
2
0.087
m
3
kmol
b y
1
b
1
y
2
b
2
10.3962 10.04282 10.6042 10.11622
8.113 bar
a
m
3
kmol
b
2
a 1y
1
a
1
1
2
y
2
a
1
2
2
2
2
30.396 12.2932
1
2
0.604 113.862
1
2
4
2
a
2
13.86 bar a
m
3
kmol
b
2
,
b
2
0.1162
m
3
kmol
a
1
2.293 bar a
m
3
kmol
b
2
,
b
1
0.0428
m
3
kmol
70.4 bar
p
ZnR
T
V
Z
RT
v
0.88
18314215112
10.5312010
5
0
