Moran M.J., Shapiro H.N. Fundamentals of Engineering Thermodynamics

Подождите немного. Документ загружается.

426 Chapter 9 Gas Power Systems

COMPRESSIBLE FLOW THROUGH

NOZZLES AND DIFFUSERS

In many applications of engineering interest, gases move at relatively high velocities and exhibit

appreciable changes in density. The flows through the nozzles and diffusers of jet engines dis-

cussed in Sec. 9.9 are important examples. Other examples are the flows through wind tunnels,

shock tubes, and steam ejectors. These flows are known as compressible flows. In this part of

the chapter, we introduce some of the principles involved in analyzing compressible flows.

Stirling engine

compressible flow

place in the isothermal process 3–4 and all the heat rejected to the surroundings would occur

in the isothermal process 1–2. It can be concluded, therefore, that the thermal efficiency of

the Stirling cycle is given by the same expression as for the Carnot and Ericsson cycles.

The Ericsson and Stirling cycles are principally of theoretical interest as examples of cy-

cles that exhibit the same thermal efficiency as the Carnot cycle. However, a practical en-

gine of the piston–cylinder type that operates on a closed regenerative cycle having features

in common with the Stirling cycle has been under study in recent years. This engine is known

as Stirling engine. The Stirling engine offers the opportunity for high efficiency together

with reduced emissions from combustion products because the combustion takes place ex-

ternally and not within the cylinder as for internal combustion engines. In the Stirling en-

gine, energy is transferred to the working fluid from products of combustion, which are kept

separate. It is an external combustion engine.



9.12 Compressible Flow Preliminaries

Concepts introduced in this section play important roles in the study of compressible flows.

The momentum equation is introduced in a form applicable to the analysis of control vol-

umes at steady state. The velocity of sound is also defined, and the concepts of Mach num-

ber and stagnation state are discussed.

 9.12.1 Momentum Equation for Steady One-Dimensional Flow

The analysis of compressible flows requires the principles of conservation of mass and energy,

the second law of thermodynamics, and relations among the thermodynamic properties of the

flowing gas. In addition, Newton’s second law of motion is required. Application of Newton’s

second law of motion to systems of fixed mass (closed systems) involves the familiar form

where F is the resultant force acting on a system of mass m and a is the acceleration. The

object of the present discussion is to introduce Newton’s second law of motion in a form ap-

propriate for the study of the control volumes considered in subsequent discussions.

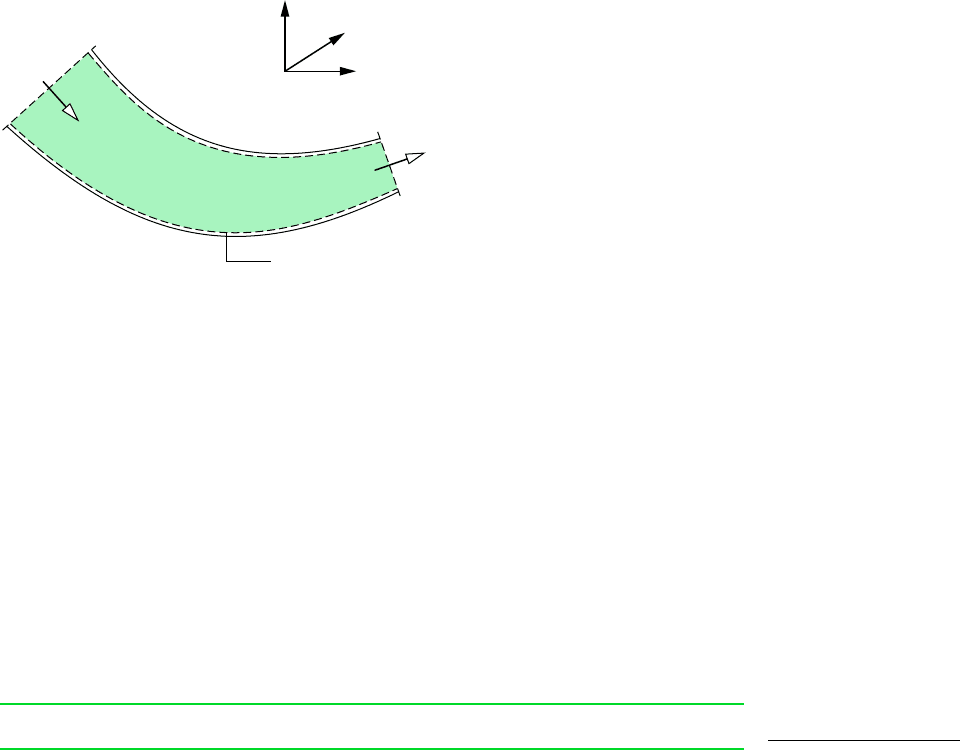
Consider the control volume shown in Fig. 9.26, which has a single inlet, designated by 1,

and a single exit, designated by 2. The flow is assumed to be one-dimensional at these lo-

cations. The energy and entropy rate equations for such a control volume have terms that ac-

count for energy and entropy transfers, respectively, at the inlets and exits. Momentum also

can be carried into or out of the control volume at the inlets and exits, and such transfers can

be accounted for as

DT (9.30) m

time rate of momentum

transfer into or

out of a control volume

accompanying mass flow

F  ma

9.12 Compressible Flow Preliminaries 427

In this expression, the momentum per unit of mass flowing across the boundary of the con-

trol volume is given by the velocity vector V. In accordance with the one-dimensional flow

model, the vector is normal to the inlet or exit and oriented in the direction of flow

In words, Newton’s second law of motion for control volumes is

At steady state, the total amount of momentum contained in the control volume is constant

with time. Accordingly, when applying Newton’s second law of motion to control volumes

at steady state, it is necessary to consider only the momentum accompanying the incoming

and outgoing streams of matter and the forces acting on the control volume. Newton’s law

then states that the resultant force F acting on the control volume equals the difference be-

tween the rates of momentum exiting and entering the control volume accompanying mass

flow. This is expressed by the following momentum equation

(9.31)

Since at steady state, the common mass flow is designated in this expression sim-

ply as The resultant force includes the forces due to pressure acting at the inlet and exit,

forces acting on the portion of the boundary through which there is no mass flow, and the

force of gravity. The expression of Newton’s second law of motion given by Eq. 9.31 suf-

fices for subsequent discussions. More general control volume formulations are normally

provided in fluid mechanics texts.

 9.12.2 Velocity of Sound and Mach Number

A sound wave is a small pressure disturbance that propagates through a gas, liquid, or solid

at a velocity c that depends on the properties of the medium. In this section we obtain an ex-

pression that relates the velocity of sound, or sonic velocity, to other properties. The veloc-

ity of sound is an important property in the study of compressible flows.

MODELING PRESSURE WAVES. Let us begin by referring to Fig. 9.27a, which shows a

pressure wave moving to the right with a velocity of magnitude c. The wave is generated by

a small displacement of the piston. As shown on the figure, the pressure, density, and tem-

perature in the region to the left of the wave depart from the respective values of the undis-

turbed fluid to the right of the wave, which are designated simply p, , and T. After the wave

has passed, the fluid to its left is in steady motion with a velocity of magnitude V.

 m

F  m

 m

 m

 V

time rate of change

of momentum contained

within the control volume

§ £

resultant force

acting on the

control volume

§ £

net rate at which momentum is

transferred into the control

volume accompanying mass flow

no flow through this

portion of the boundary

 Figure 9.26 One-inlet, one-

exit control volume at steady state

labeled with momentum transfers

accompanying mass flow.

momentum equation

428 Chapter 9 Gas Power Systems

Figure 9.27a shows the wave from the point of view of a stationary observer. It is easier

to analyze this situation from the point of view of an observer at rest relative to the wave,

as shown in Fig. 9.27b. By adopting this viewpoint, a steady-state analysis can be applied to

the control volume identified on the figure. To an observer at rest relative to the wave, it ap-

pears as though the fluid is moving toward the stationary wave from the right with velocity

c, pressure p, density , and temperature T and moving away on the left with velocity c V,

pressure p p, density  , and temperature T T.

At steady state, the conservation of mass principle for the control volume reduces to

On rearrangement

(9.32)

If the disturbance is weak, the third term on the right of Eq. 9.32 can be neglected, leaving

(9.33)

Next, the momentum equation, Eq. 9.31, is applied to the control volume under con-

sideration. Since the thickness of the wave is small, shear forces at the wall are negligi-

ble. The effect of gravity is also ignored. Hence, the only significant forces acting on the

control volume in the direction of flow are the forces due to pressure at the inlet and exit.

With these idealizations, the component of the momentum equation in the direction of flow

reduces to

(9.34)

Combining Eqs. 9.33 and 9.34 and solving for c

(9.35)

c 

¢p

¢r

¢p  rc ¢V

 1rAc21¢V2

 m

1c  ¢V  c2

pA  1p  ¢p2

A  m

1c  ¢V2 m

¢V  1c



r2¢r

0  c

¢r  r¢V  ¢r¢V

rAc  1r  ¢r2A1c  ¢V2

 m

p, T, ρ

(a)(b)

p, ρ, T

∆V

p + ∆p

ρ + ∆ρ

T + ∆T

c – ∆V

p + ∆p

ρ + ∆ρ

T + ∆T

V = 0

Piston

Stationary

observer

Control volume for an

observer moving with

the wave

Observer on

wave

Undisturbed fluid

 Figure 9.27 Illustrations used to analyze the propagation of a sound wave. (a) Propagation of a

pressure wave through a quiescent fluid, relative to a stationary observer. (b) Observer at rest relative

to the wave.

9.12 Compressible Flow Preliminaries 429

SOUND WAVES. For all sound waves the differences in pressure, density, and temperature

across the wave are quite small. In particular,   , justifying the neglect of the third

term of Eq. 9.32. Furthermore, the ratio p in Eq. 9.35 can be interpreted as the deriv-

ative of pressure with respect to density across the wave. Experiments also indicate that the

relation between pressure and density across a sound wave is nearly isentropic. The expres-

sion for the velocity of sound then becomes

(9.36a)

or in terms of specific volume

(9.36b)

The velocity of sound is an intensive property whose value depends on the state of the medium

through which sound propagates. Although we have assumed that sound propagates isen-

tropically, the medium itself may be undergoing any process.

Means for evaluating the velocity of sound c for gases, liquids, and solids are introduced

in Sec. 11.5. The special case of an ideal gas will be considered here because it is used

extensively later in the chapter. For this case, the relationship between pressure and specific

volume of an ideal gas at fixed entropy is pv

 constant, where k is the specific heat ratio

(Sec. 6.7). Thus, (0p0v)

kpv, and Eq. 9.36b gives Or, with the ideal gas

equation of state

(9.37)

 for example. . .

to illustrate the use of Eq. 9.37, let us calculate the velocity of

sound in air at 300 K and 650 K. From Table A-20 at 300 K, k  1.4. Thus

At 650 K, k  1.37, and c  506 m/s, as can be verified.



MACH NUMBER. In subsequent discussions, the ratio of the velocity V at a state in a flow-

ing fluid to the value of the sonic velocity c at the same state plays an important role. This

ratio is called the Mach number M

(9.38)

When M  1, the flow is said to be supersonic; when M  1, the flow is subsonic; and

when M  1, the flow is sonic. The term hypersonic is used for flows with Mach numbers

much greater than one, and the term transonic refers to flows where the Mach number is

close to unity.

M 

c 

1.4

8314

28.97

b 1300 K2`

1 kg

1 N

` 347

c  2kRT

1ideal gas2

c  1kpv.

c 

v

c 

velocity of sound

Mach number

supersonic

subsonic

430 Chapter 9 Gas Power Systems

 9.12.3 Determining Stagnation State Properties

When dealing with compressible flows, it is often convenient to work with properties eval-

uated at a reference state known as the stagnation state. The stagnation state is the state a

flowing fluid would attain if it were decelerated to zero velocity isentropically. We might

imagine this as taking place in a diffuser operating at steady state. By reducing an energy

balance for such a diffuser, it can be concluded that the enthalpy at the stagnation state as-

sociated with an actual state in the flow where the specific enthalpy is h and the velocity is

V is given by

(9.39)

The enthalpy designated here as h

is called the stagnation enthalpy. The pressure p

and

temperature T

at a stagnation state are called the stagnation pressure and stagnation

temperature, respectively.

 h 

stagnation state

stagnation enthalpy

stagnation pressure

and temperature



9.13 Analyzing One-Dimensional Steady

Flow in Nozzles and Diffusers

Although the subject of compressible flow arises in a great many important areas of engi-

neering application, the remainder of this presentation is concerned only with flow through

nozzles and diffusers. Texts dealing with compressible flow should be consulted for discus-

sion of other areas of application.

In the present section we determine the shapes required by nozzles and diffusers for sub-

sonic and supersonic flow. This is accomplished using mass, energy, entropy, and momen-

tum principles, together with property relationships. In addition, we study how the flow

through nozzles is affected as conditions at the nozzle exit are changed. The presentation

concludes with an analysis of normal shocks, which can exist in supersonic flows.

 9.13.1 Exploring the Effects of Area Change in Subsonic and

Supersonic Flows

The objective of the present discussion is to establish criteria for determining whether a

nozzle or diffuser should have a converging, diverging, or converging–diverging shape.

This is accomplished using differential equations relating the principal variables that are

obtained using mass and energy balances together with property relations, as considered

next.

GOVERNING DIFFERENTIAL EQUATIONS. Let us begin by considering a control volume

enclosing a nozzle or diffuser. At steady state, the mass flow rate is constant, so

In differential form

or on dividing each term by AV

(9.40)



 0

AV dr  rA dV  rV dA  0

d1rAV2 0

rAV  constant

9.13 Analyzing One-Dimensional Steady Flow in Nozzles and Diffusers 431

Assuming and negligible potential energy effects, an energy rate balance

reduces to give

Introducing Eq. 9.39, it follows that the stagnation enthalpies at states 1 and 2 are equal:

 h

. Since any state downstream of the inlet can be regarded as state 2, the following

relationship between the specific enthalpy and kinetic energy must be satisfied at each state

(constant)

In differential form this becomes

(9.41)

This equation shows that if the velocity increases (decreases) in the direction of flow, the

specific enthalpy must decrease (increase) in the direction of flow, and conversely.

In addition to Eqs. 9.40 and 9.41 expressing conservation of mass and energy, relation-

ships among properties must be taken into consideration. Assuming the flow occurs isen-

tropically, the property relation (Eq. 6.12b)

reduces to give

(9.42)

This equation shows that when pressure increases or decreases in the direction of flow, the

specific enthalpy changes in the same way.

Forming the differential of the property relation p  p(, s)

The second term vanishes in isentropic flow. Introducing Eq. 9.36a, we have

(9.43)

which shows that when pressure increases or decreases in the direction of flow, density

changes in the same way.

Additional conclusions can be drawn by combining the above differential equations. Com-

bining Eqs. 9.41 and 9.42 results in

(9.44)

which shows that if the velocity increases (decreases) in the direction of flow, the pressure

must decrease (increase) in the direction of flow, and conversely.

Eliminating dp between Eqs. 9.43 and 9.44 and combining the result with Eq. 9.40 gives



c1  a

dp V dV

dp  c

dp  a

dr  a

dh 

T ds  dh 

dh V dV

h 

 h



 h



 W

 0

432 Chapter 9 Gas Power Systems

or with the Mach number M

(9.45)

VARIATION OF AREA WITH VELOCITY. Equation 9.45 shows how area must vary with ve-

locity. The following four cases can be identified:

Case 1: Subsonic nozzle. dV  0, M  1 1 dA  0: The duct converges in the direction

of flow.

Case 2: Supersonic nozzle. dV  0, M  1 1 dA  0: The duct diverges in the direction

of flow.

Case 3: Supersonic diffuser. dV  0, M  1 1 dA  0: The duct converges in the direction

of flow.

Case 4: Subsonic diffuser. dV  0, M  1 1 dA  0: The duct diverges in the direction

of flow.

The conclusions reached above concerning the nature of the flow in subsonic and super-

sonic nozzles and diffusers are summarized in Fig. 9.28. From Fig. 9.28a, we see that to ac-

celerate a fluid flowing subsonically, a converging nozzle must be used, but once M  1 is

achieved, further acceleration can occur only in a diverging nozzle. From Fig. 9.28b, we see

that a converging diffuser is required to decelerate a fluid flowing supersonically, but once

M  1 is achieved, further deceleration can occur only in a diverging diffuser. These findings

suggest that a Mach number of unity can occur only at the location in a nozzle or diffuser

where the cross-sectional area is a minimum. This location of minimum area is called the

throat.

The developments of this section have not required the specification of an equation of

state; thus, the conclusions hold for all gases. Moreover, although the conclusions have been

drawn under the restriction of isentropic flow through nozzles and diffusers, they are at least

qualitatively valid for actual flows because the flow through well-designed nozzles and dif-

fusers is nearly isentropic. Isentropic nozzle efficiencies (Sec. 6.8) in excess of 95% can be

attained in practice.

 9.13.2 Effects of Back Pressure on Mass Flow Rate

In the present discussion we consider the effect of varying the back pressure on the rate of

mass flow through nozzles. The back pressure is the pressure in the exhaust region outside

the nozzle. The case of converging nozzles is taken up first and then converging–diverging

nozzles are considered.



11  M

M < 1

Subsonic

M > 1

Supersonic

Case 4

(b)

Case 3

M > 1

Supersonic

M < 1

Subsonic

Case 2

(a)

Case 1

 Figure 9.28 Effects of area change in subsonic and supersonic flows. (a) Nozzles:

V increases; h, p, and r decrease. (b) Diffusers: V decreases h, p, and  increase.

throat

back pressure

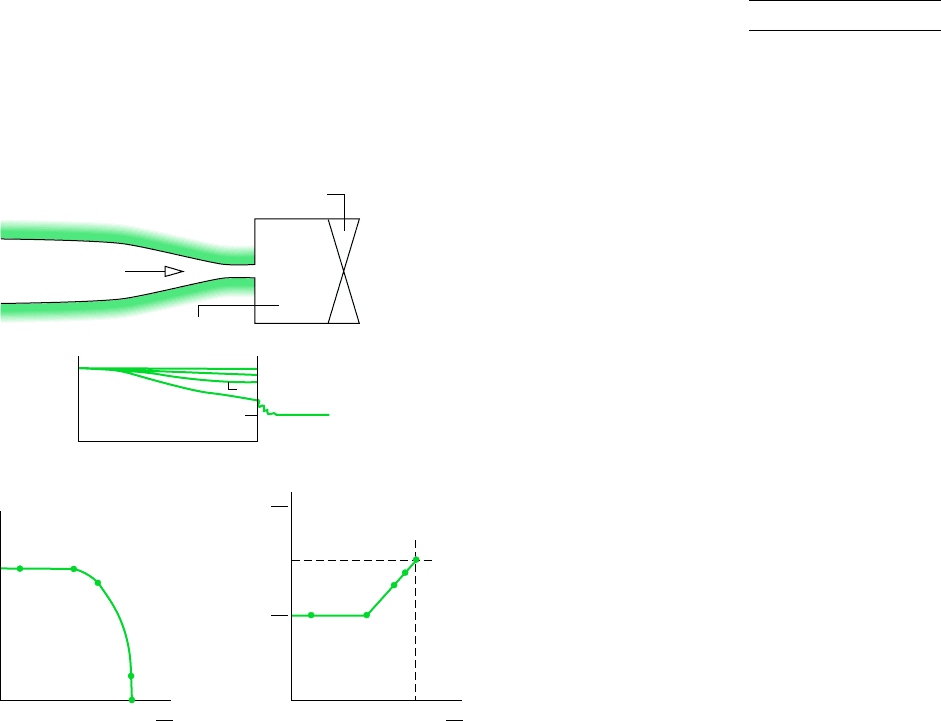
CONVERGING NOZZLES. Figure 9.29 shows a converging duct with stagnation condi-

tions at the inlet, discharging into a region in which the back pressure p

can be varied.

For the series of cases labeled a through e, let us consider how the mass flow rate and

nozzle exit pressure p

vary as the back pressure is decreased while keeping the inlet

conditions fixed.

When p

 p

, there is no flow, so This corresponds to case a of Fig. 9.29.

If the back pressure p

is decreased, as in cases b and c, there will be flow through the noz-

zle. As long as the flow is subsonic at the exit, information about changing conditions in the

exhaust region can be transmitted upstream. Decreases in back pressure thus result in greater

mass flow rates and new pressure variations within the nozzle. In each instance, the veloc-

ity is subsonic throughout the nozzle and the exit pressure equals the back pressure. The exit

Mach number increases as p

decreases, however, and eventually a Mach number of unity

will be attained at the nozzle exit. The corresponding pressure is denoted by p*, called the

critical pressure. This case is represented by d on Fig. 9.29.

Recalling that the Mach number cannot increase beyond unity in a converging section, let

us consider next what happens when the back pressure is reduced further to a value less than

p*, such as represented by case e. Since the velocity at the exit equals the velocity of sound,

information about changing conditions in the exhaust region no longer can be transmitted

upstream past the exit plane. Accordingly, reductions in p

below p* have no effect on flow

conditions in the nozzle. Neither the pressure variation within the nozzle nor the mass flow

rate is affected. Under these conditions, the nozzle is said to be choked. When a nozzle is

choked, the mass flow rate is the maximum possible for the given stagnation conditions. For

less than p*, the flow expands outside the nozzle to match the lower back pressure, as

shown by case e of Fig. 9.29. The pressure variation outside the nozzle cannot be predicted

using the one-dimensional flow model.

 0.

9.13 Analyzing One-Dimensional Steady Flow in Nozzles and Diffusers 433

1.0

 Figure 9.29 Effect of

back pressure on the operation

of a converging nozzle.

choked flow:

converging nozzle

, T

V ≈ 0

1.0

Exhaust region

Valve to adjust

back pressure

434 Chapter 9 Gas Power Systems

choked flow:

converging–diverging

nozzle

normal shock

, T

V ≈ 0

M = 1

Exhaust region

Throat

Valve to adjust

back pressure

Normal

shock

Normal

shock

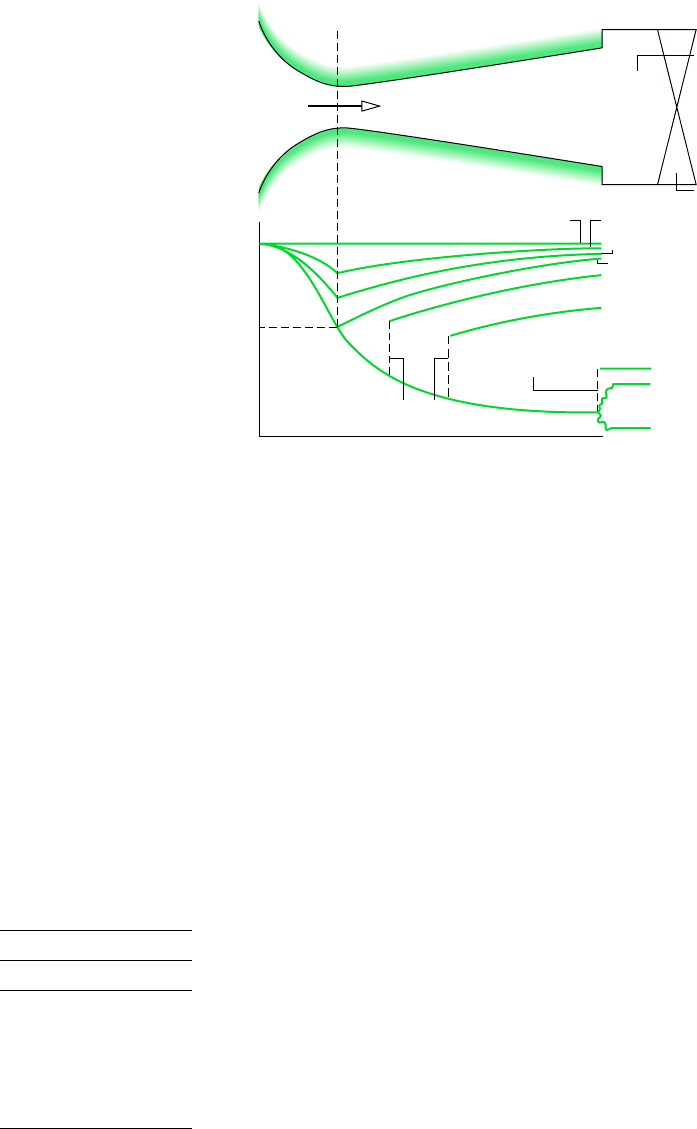
 Figure 9.30 Effect of back pressure on the operation of a converging–

diverging nozzle.

CONVERGING–DIVERGING NOZZLES. Figure 9.30 illustrates the effects of varying back

pressure on a converging–diverging nozzle. The series of cases labeled a through j is con-

sidered next.

 Let us first discuss the cases designated a, b, c, and d. Case a corresponds to p



 p

for which there is no flow. When the back pressure is slightly less than p

(case b), there is some flow, and the flow is subsonic throughout the nozzle. In accor-

dance with the discussion of Fig. 9.28, the greatest velocity and lowest pressure occur at

the throat, and the diverging portion acts as a diffuser in which pressure increases and

velocity decreases in the direction of flow. If the back pressure is reduced further, corre-

sponding to case c, the mass flow rate and velocity at the throat are greater than before.

Still, the flow remains subsonic throughout and qualitatively the same as case b. As the

back pressure is reduced, the Mach number at the throat increases, and eventually a

Mach number of unity is attained there (case d). As before, the greatest velocity and

lowest pressure occur at the throat, and the diverging portion remains a subsonic

diffuser. However, because the throat velocity is sonic, the nozzle is now choked: The

maximum mass flow rate has been attained for the given stagnation conditions. Further

reductions in back pressure cannot result in an increase in the mass flow rate.

 When the back pressure is reduced below that corresponding to case d, the flow through

the converging portion and at the throat remains unchanged. Conditions within the di-

verging portion can be altered, however, as illustrated by cases e, f, and g. In case e, the

fluid passing the throat continues to expand and becomes supersonic in the diverging

portion just downstream of the throat; but at a certain location an abrupt change in

properties occurs. This is called a normal shock. Across the shock, there is a rapid and

irreversible increase in pressure, accompanied by a rapid decrease from supersonic to

subsonic flow. Downstream of the shock, the diverging duct acts as a subsonic diffuser

in which the fluid continues to decelerate and the pressure increases to match the back

pressure imposed at the exit. If the back pressure is reduced further (case f), the loca-

tion of the shock moves downstream, but the flow remains qualitatively the same as in

9.13 Analyzing One-Dimensional Steady Flow in Nozzles and Diffusers 435

case e. With further reductions in back pressure, the shock location moves farther down-

stream of the throat until it stands at the exit (case g). In this case, the flow throughout

the nozzle is isentropic, with subsonic flow in the converging portion, M  1 at the

throat, and supersonic flow in the diverging portion. Since the fluid leaving the nozzle

passes through a shock, it is subsonic just downstream of the exit plane.

 Finally, let us consider cases h, i, and j where the back pressure is less than that corre-

sponding to case g. In each of these cases, the flow through the nozzle is not affected.

The adjustment to changing back pressure occurs outside the nozzle. In case h, the pres-

sure decreases continuously as the fluid expands isentropically through the nozzle and

then increases to the back pressure outside the nozzle. The compression that occurs out-

side the nozzle involves oblique shock waves. In case i, the fluid expands isentropically

to the back pressure and no shocks occur within or outside the nozzle. In case j, the

fluid expands isentropically through the nozzle and then expands outside the nozzle to

the back pressure through oblique expansion waves. Once M  1 is achieved at the

throat, the mass flow rate is fixed at the maximum value for the given stagnation

conditions, so the mass flow rate is the same for back pressures corresponding to cases

d through j. The pressure variations outside the nozzle involving oblique waves cannot

be predicted using the one-dimensional flow model.

 9.13.3 Flow Across a Normal Shock

We have seen that under certain conditions a rapid and abrupt change of state called a shock

takes place in the diverging portion of a supersonic nozzle. In a normal shock, this change

of state occurs across a plane normal to the direction of flow. The object of the present dis-

cussion is to develop means for determining the change of state across a normal shock.

MODELING NORMAL SHOCKS. A control volume enclosing a normal shock is shown in

Fig. 9.31. The control volume is assumed to be at steady state with and

negligible effects of potential energy. The thickness of the shock is very small (on the order of

5

cm). Thus, there is no significant change in flow area across the shock, even though it may

occur in a diverging passage, and the forces acting at the wall can be neglected relative to the

pressure forces acting at the upstream and downstream locations denoted by x and y, respectively.

The upstream and downstream states are related by the following equations:

Mass:

(9.46)

Energy:

(9.47a)

(9.47b)

Momentum:

(9.48)

Entropy:

(9.49)

When combined with property relations for the particular fluid under consideration,

Eqs. 9.46, 9.47, and 9.48 allow the downstream conditions to be determined for specified

upstream conditions. Equation 9.49, which corresponds to Eq. 6.41, leads to the important

 s

 s



 p

 r

 r

 h



 h



 r

 0, Q

 0