Moran M.J., Shapiro H.N. Fundamentals of Engineering Thermodynamics

Подождите немного. Документ загружается.

396 Chapter 9 Gas Power Systems

Analysis: The net work of the cycle per unit of mass flow is

Since c

is constant (assumption 6)

Or on rearrangement

Replacing the temperature ratios T

T

and T

T

by using Eqs. 9.23 and 9.24, respectively, gives

From this expression it can be concluded that for specified values of T

, T

, and c

, the value of the net work output per unit

of mass flow varies with the pressure ratio p

p

only.

To determine the pressure ratio that maximizes the net work output per unit of mass flow, first form the derivative

When the partial derivative is set to zero, the following relationship is obtained

By checking the sign of the second derivative, we can verify that the net work per unit of mass flow is a maximum when this

relationship is satisfied.

For gas turbines intended for transportation, it is desirable to keep engine size small. Thus, the gas turbine should operate

near the compressor pressure ratio that yields the most work per unit of mass flow. The present example provides an elementary

illustration of how the compressor pressure ratio for maximum net work per unit of mass flow is affected by the constraint of

a fixed turbine inlet temperature.

 a



321k124

 c

k  1

bca

b a

12k 12



 a

1



 c

k  1

bca

b a

1



 a

1



0 1W

cycle



0 1 p





0 1p





1k 12



 a

1k 12



 1 df

cycle

 c



1k 12



 a

1k 12



 1 d

cycle

 c



 1b

cycle

 c

31T

 T

2 1T

 T

cycle

 1h

 h

2 1h

 h

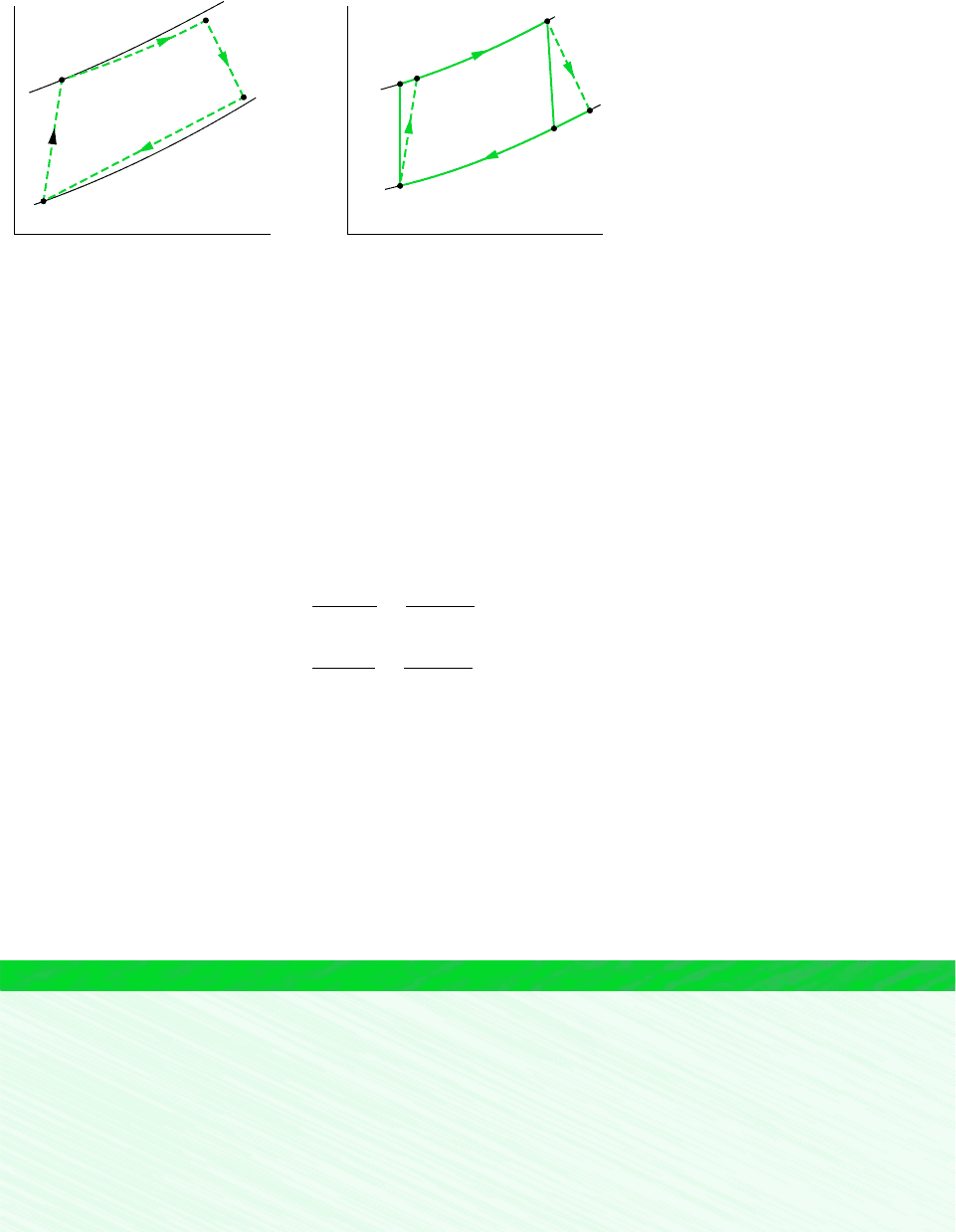
 9.6.3 Considering Gas Turbine Irreversibilities and Losses

The principal state points of an air-standard gas turbine might be shown more realisti-

cally as in Fig. 9.13a. Because of frictional effects within the compressor and turbine, the

working fluid would experience increases in specific entropy across these components.

Owing to friction, there also would be pressure drops as the working fluid passes through

the heat exchangers. However, because frictional pressure drops are less significant sources

of irreversibility, we ignore them in subsequent discussions and for simplicity show the

flow through the heat exchangers as occurring at constant pressure. This is illustrated by

Fig. 9.13b. Stray heat transfers from the power plant components to the surroundings rep-

resent losses, but these effects are usually of secondary importance and are also ignored

in subsequent discussions.

9.6 Air-Standard Brayton Cycle 397

As the effect of irreversibilities in the turbine and compressor becomes more pronounced,

the work developed by the turbine decreases and the work input to the compressor increases,

resulting in a marked decrease in the net work of the power plant. Accordingly, if an appre-

ciable amount of net work is to be developed by the plant, relatively high turbine and com-

pressor efficiencies are required. After decades of developmental effort, efficiencies of 80 to

90% can now be achieved for the turbines and compressors in gas turbine power plants. Des-

ignating the states as in Fig. 9.13b, the isentropic turbine and compressor efficiencies are

given by

The effects of irreversibilities in the turbine and compressor are important. Still, among

the irreversibilities of actual gas turbine power plants, combustion irreversibility is the most

significant by far. An air-standard analysis does not allow this irreversibility to be evaluated,

however, and means introduced in Chap. 13 must be applied. Combustion irreversibility is

also briefly considered in Sec. 9.10.

Example 9.6 brings out the effect of turbine and compressor irreversibilities on plant

performance.







 h







 h

(a)

p = c

(b)

p = c

 Figure 9.13 Effects of irreversibilities on the air-standard gas turbine.

EXAMPLE 9.6 Brayton Cycle with Irreversibilities

Reconsider Example 9.4, but include in the analysis that the turbine and compressor each have an isentropic efficiency of

80%. Determine for the modified cycle (a) the thermal efficiency of the cycle, (b) the back work ratio, (c) the net power de-

veloped, in kW.

SOLUTION

Known: An air-standard Brayton cycle operates with given compressor inlet conditions, given turbine inlet temperature, and

known compressor pressure ratio. The compressor and turbine each have an isentropic efficiency of 80%.

Find: Determine the thermal efficiency, the back work ratio, and the net power developed, in kW.

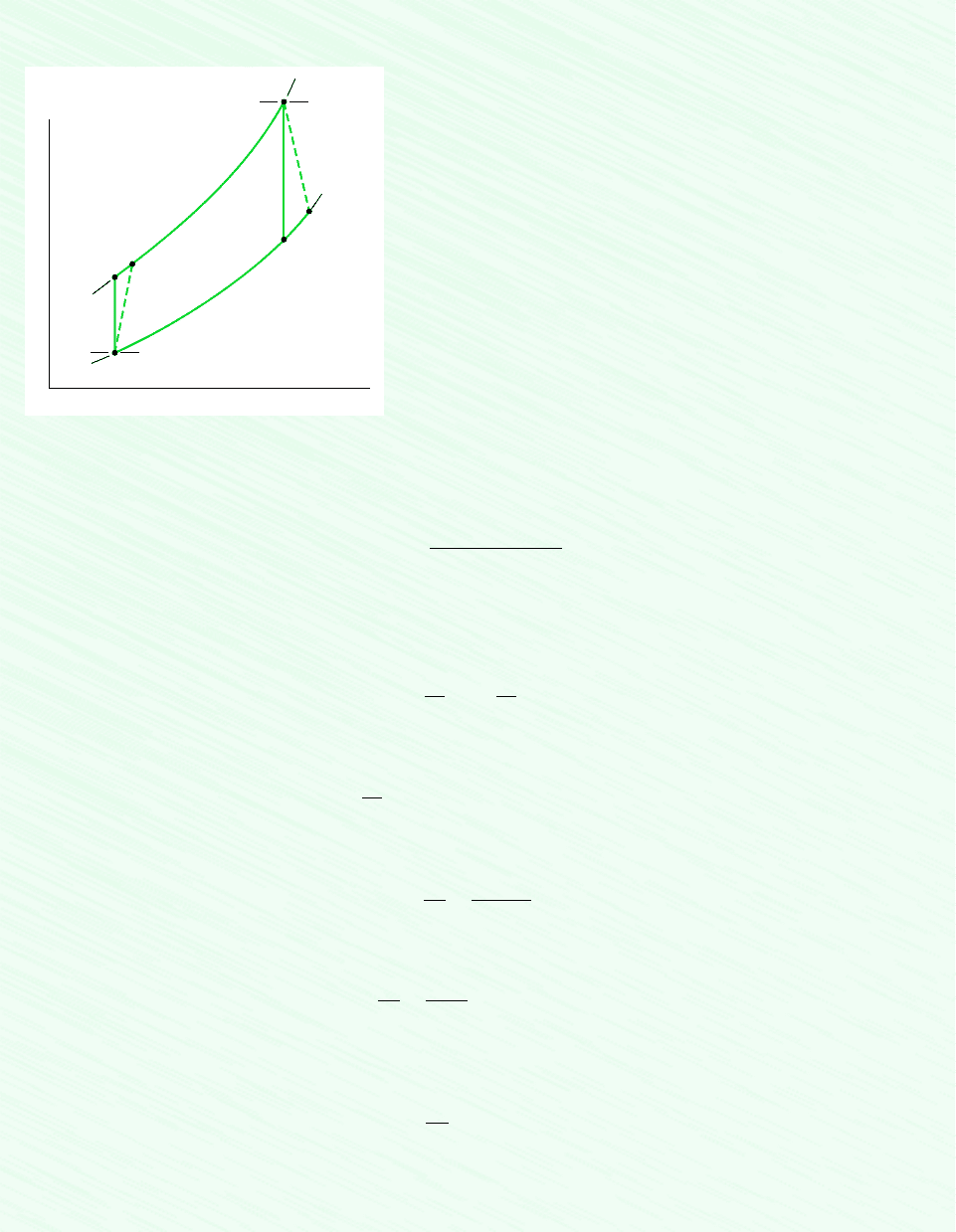
398 Chapter 9 Gas Power Systems

Schematic and Given Data:

= 300 K

p = 1000 kPa

p = 100 kPa

= 1400 K

 Figure E9.6

Assumptions:

1. Each component is analyzed as a control volume at steady state.

2. The compressor and turbine are adiabatic.

3. There are no pressure drops for flow through the heat exchangers.

4. Kinetic and potential energy effects are negligible.

5. The working fluid is air modeled as an ideal gas.

Analysis:

(a) The thermal efficiency is given by

The work terms in the numerator of this expression are evaluated using the given values of the compressor and turbine isen-

tropic efficiencies as follows:

The turbine work per unit of mass is

where 

is the turbine efficiency. The value of ( )

is determined in the solution to Example 9.4 as 706.9 kJ/kg. Thus

For the compressor, the work per unit of mass is

where 

is the compressor efficiency. The value of ( )

is determined in the solution to Example 9.4 as 279.7 kJ/kg, so

The specific enthalpy at the compressor exit, h

, is required to evaluate the denominator of the thermal efficiency expres-

sion. This enthalpy can be determined by solving

to obtain

 h

 W



 h

 h



279.7

0.8

 349.6 kJ/kg







 0.81706.92 565.5 kJ/kg



 h

h 



2 1W



❶

9.7 Regenerative Gas Turbines 399

The turbine exhaust temperature of a gas turbine is normally well above the ambient tem-

perature. Accordingly, the hot turbine exhaust gas has a potential for use (exergy) that would

be irrevocably lost were the gas discarded directly to the surroundings. One way of utilizing

this potential is by means of a heat exchanger called a regenerator, which allows the air ex-

iting the compressor to be preheated before entering the combustor, thereby reducing the

amount of fuel that must be burned in the combustor. The combined cycle arrangement con-

sidered in Sec. 9.10 is another way to utilize the hot turbine exhaust gas.

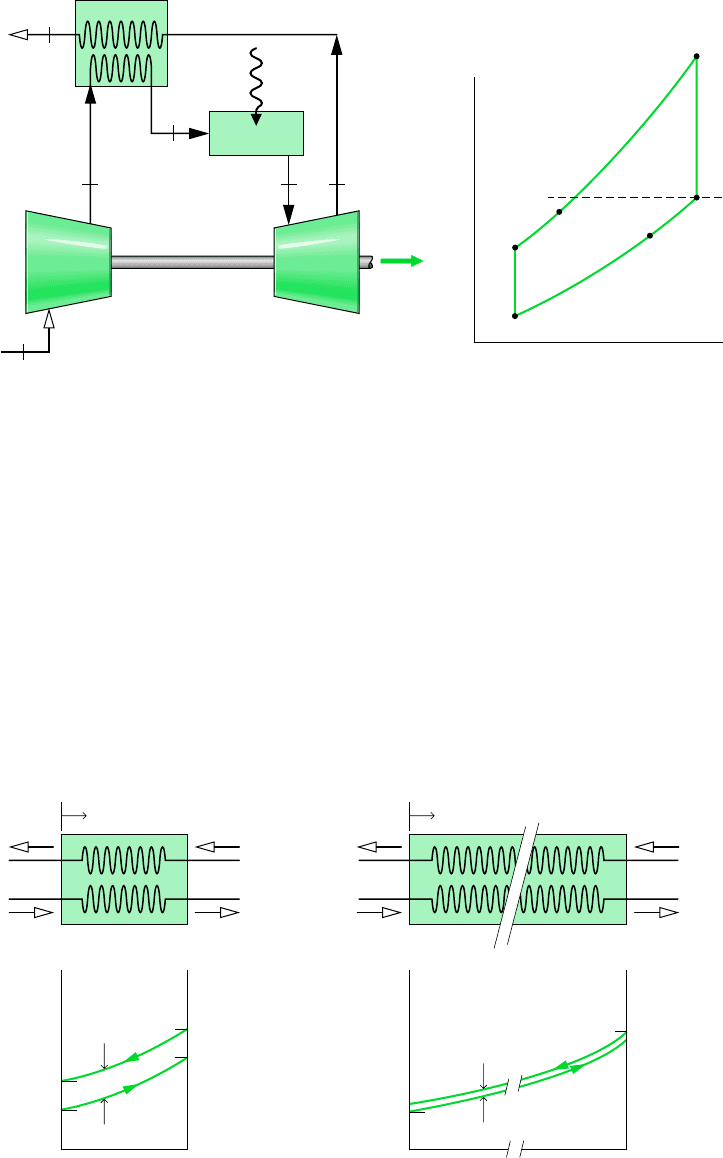
An air-standard Brayton cycle modified to include a regenerator is illustrated in Fig. 9.14.

The regenerator shown is a counterflow heat exchanger through which the hot turbine ex-

haust gas and the cooler air leaving the compressor pass in opposite directions. Ideally, no

frictional pressure drop occurs in either stream. The turbine exhaust gas is cooled from state 4

to state y, while the air exiting the compressor is heated from state 2 to state x. Hence, a heat

transfer from a source external to the cycle is required only to increase the air temperature

from state x to state 3, rather than from state 2 to state 3, as would be the case without

regeneration. The heat added per unit of mass is then given by

(9.26)

 h

 h

Inserting known values

The heat transfer to the working fluid per unit of mass flow is then

where h

is from the solution to Example 9.4.

Finally, the thermal efficiency is

(b) The back work ratio is

The solution to this example on a cold air-standard basis is left as an exercise.

Irreversibilities within the turbine and compressor have a significant impact on the performance of gas turbines. This is

brought out by comparing the results of the present example with those of Example 9.4. Irreversibilities result in an in-

crease in the work of compression and a reduction in work output of the turbine. The back work ratio is greatly increased

and the thermal efficiency significantly decreased.

cycle

 a5.807

b 1565.5  349.62

1 kW

1 kJ/s

` 1254 kW

bwr 





349.6

565.5

 0.618 161.8%2

h 

565.5  349.6

865.6

 0.249 124.9%2

 h

 h

 1515.4  649.8  865.6 kJ/kg

 300.19  349.6  649.8 kJ/kg



9.7 Regenerative Gas Turbines

regenerator

❶

❷

400 Chapter 9 Gas Power Systems

The net work developed per unit of mass flow is not altered by the addition of a regenera-

tor. Thus, since the heat added is reduced, the thermal efficiency increases.

REGENERATOR EFFECTIVENESS. From Eq. 9.26 it can be concluded that the external

heat transfer required by a gas turbine power plant decreases as the specific enthalpy

increases and thus as the temperature T

increases. Evidently, there is an incentive in

terms of fuel saved for selecting a regenerator that provides the greatest practical value

for this temperature. To consider the maximum theoretical value for T

, refer to Fig. 9.15,

which shows temperature variations of the hot and cold streams of a counterflow heat

exchanger.

Combustor

234

TurbineCompressor

cycle

Regenerator

 Figure 9.14 Regenerative air-standard gas turbine cycle.

∆T

(a)(b)

Hot

Cold

hot, in

cold, out

hot, out

cold, in

∆T → 0

Hot

Cold

hot, in

cold, in

Hotter

stream in

Colder

stream in

Colder

stream in

Hotter

stream in

 Figure 9.15 Temperature distributions in counterflow heat exchangers. (a) Actual.

(b) Reversible.

9.7 Regenerative Gas Turbines 401

 First, refer to Fig. 9.15a. Since a finite temperature difference between the streams is

required for heat transfer to occur, the temperature of the cold stream at each loca-

tion, denoted by the coordinate z, is less than that of the hot stream. In particular,

the temperature of the colder stream as it exits the heat exchanger is less than the

temperature of the incoming hot stream. If the heat transfer area were increased,

providing more opportunity for heat transfer between the two streams, there would be

a smaller temperature difference at each location.

 In the limiting case of infinite heat transfer area, the temperature difference would

approach zero at all locations, as illustrated in Fig. 9.15b, and the heat transfer would

approach reversibility. In this limit, the exit temperature of the colder stream would

approach the temperature of the incoming hot stream. Thus, the highest possible

temperature that could be achieved by the colder stream is the temperature of the

incoming hot gas.

Referring again to the regenerator of Fig. 9.14, we can conclude from the discussion of

Fig. 9.15 that the maximum theoretical value for the temperature T

is the turbine exhaust

temperature T

, obtained if the regenerator were operating reversibly. The regenerator effec-

tiveness, 

reg

, is a parameter that gauges the departure of an actual regenerator from such an

ideal regenerator. The regenerator effectiveness is defined as the ratio of the actual enthalpy

increase of the air flowing through the compressor side of the regenerator to the maximum

theoretical enthalpy increase. That is,

(9.27)

As heat transfer approaches reversibility, h

approaches h

and tends to unity (100%).

In practice, regenerator effectiveness values typically range from 60 to 80%, and thus the

temperature T

of the air exiting on the compressor side of the regenerator is normally well

below the turbine exhaust temperature. To increase the effectiveness above this range would

require greater heat transfer area, resulting in equipment costs that might cancel any advan-

tage due to fuel savings. Moreover, the greater heat transfer area that would be required for

a larger effectiveness can result in a significant frictional pressure drop for flow through the

regenerator, thereby affecting overall performance. The decision to add a regenerator is in-

fluenced by considerations such as these, and the final decision is primarily an economic

one.

In Example 9.7, we analyze an air-standard Brayton cycle with regeneration and explore

the effect on thermal efficiency as the regenerator effectiveness varies.

reg



 h

EXAMPLE 9.7 Brayton Cycle with Regeneration

A regenerator is incorporated in the cycle of Example 9.4. (a) Determine the thermal efficiency for a regenerator effective-

ness of 80%. (b) Plot the thermal efficiency versus regenerator effectiveness ranging from 0 to 80%.

SOLUTION

Known: A regenerative gas turbine operates with air as the working fluid. The compressor inlet state, turbine inlet temper-

ature, and compressor pressure ratio are known.

Find: For a regenerator effectiveness of 80%, determine the thermal efficiency. Also plot the thermal efficiency versus the

regenerator effectiveness ranging from 0 to 80%.

regenerator effectiveness

402 Chapter 9 Gas Power Systems

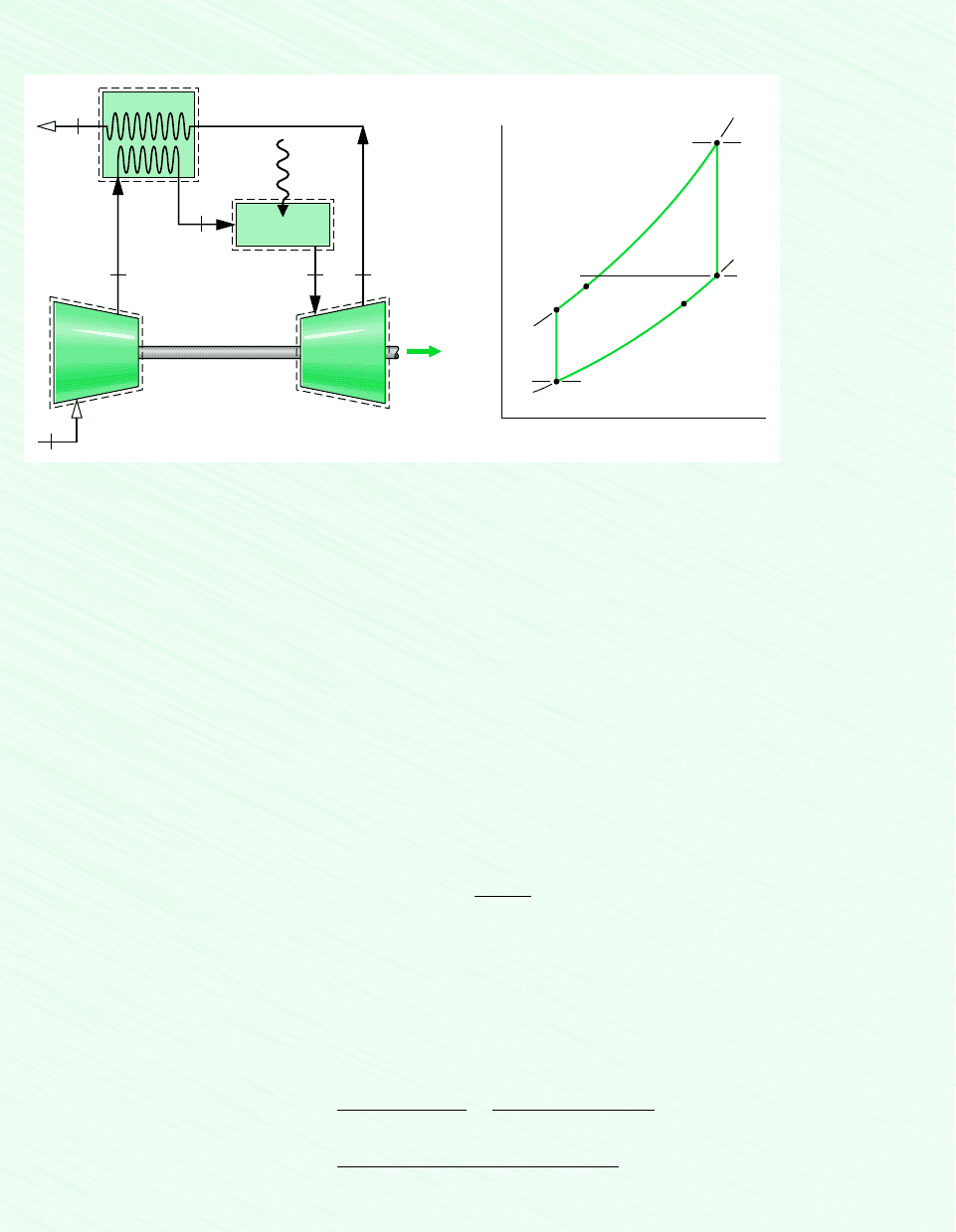
Schematic and Given Data:

Combustor

234

TurbineCompressor

reg

80%

cycle

Regenerator

= 1400 K

= 300 K

= 100 kPa

= 300 K

p = 1000 kPa

p = 100 kPa

= 1400 K

 Figure E9.7a

Assumptions:

1. Each component is analyzed as a control volume at steady state. The control volumes are shown on the accompanying

sketch by dashed lines.

2. The compressor and turbine processes are isentropic.

3. There are no pressure drops for flow through the heat exchangers.

4. The regenerator effectiveness is 80% in part (a).

5. Kinetic and potential energy effects are negligible.

6. The working fluid is air modeled as an ideal gas.

Analysis:

(a) The specific enthalpy values at the numbered states on the T–s diagram are the same as those in Example 9.4: h



300.19 kJ/kg, h

 579.9 kJ/kg, h

 1515.4 kJ/kg, h

 808.5 kJ/kg.

To find the specific enthalpy h

, the regenerator effectiveness is used as follows: By definition

Solving for h

With the specific enthalpy values determined above, the thermal efficiency is

 0.568 156.8% 2



11515.4  808.52 1579.9  300.192

11515.4  762.82

h 



2 1W





 h

2 1h

 h

 10.82

1808.5  579.92 579.9  762.8 kJ/kg

 h

reg

 h

2 h

reg



 h

❶

❷

9.7 Regenerative Gas Turbines 403

(b) The IT code for the solution follows, where 

reg

is denoted as etareg,  is eta, is Wcomp, and so on.

// Fix the states

T1 = 300 // K

p1 = 100 // kPa

h1 = h_T(“Air”, T1)

s1 = s_TP(“Air”, T1, p1)

p2 = 1000 // kPa

s2 = s_TP(“Air”, T2, p2)

s2 = s1

h2 = h_T(“Air”, T2)

T3 = 1400 // K

p3 = p2

h3 = h_T(“Air”, T3)

s3 = s_TP(“Air”, T3, p3)

p4 = p1

s4 = s_TP(“Air”, T4, p4)

s4 = s3

h4 = h_T(“Air”, T4)

etareg = 0.8

hx = etareg * (h4 – h2) + h2

// Thermal efficiency

Wcomp = h2 – h1

Wturb = h3 – h4

Qin = h3 – hx

eta = (Wturb – Wcomp)  Qin

Using the Explore button, sweep etareg from 0 to 0.8 in steps of 0.01. Then, using the Graph button, obtain the following

plot:

comp



0.1 0.3 0.5 0.70 0.2 0.4 0.6 0.8

Regenerator effectiveness

Thermal efficiency

0.1

0.2

0.3

0.4

0.5

0.6

 Figure E9.7b

From the computer data, we see that the cycle thermal efficiency increases from 0.456, which agrees closely with the result

of Example 9.4 (no regenerator), to 0.567 for a regenerator effectiveness of 80%, which agrees closely with the result of

part (a) This trend is also seen in the accompanying graph. Regenerator effectiveness is seen to have a significant effect on

cycle thermal efficiency.

The values for work per unit of mass flow of the compressor and turbine are unchanged by the addition of the regenera-

tor. Thus, the back work ratio and net work output are not affected by this modification.

❶

❸

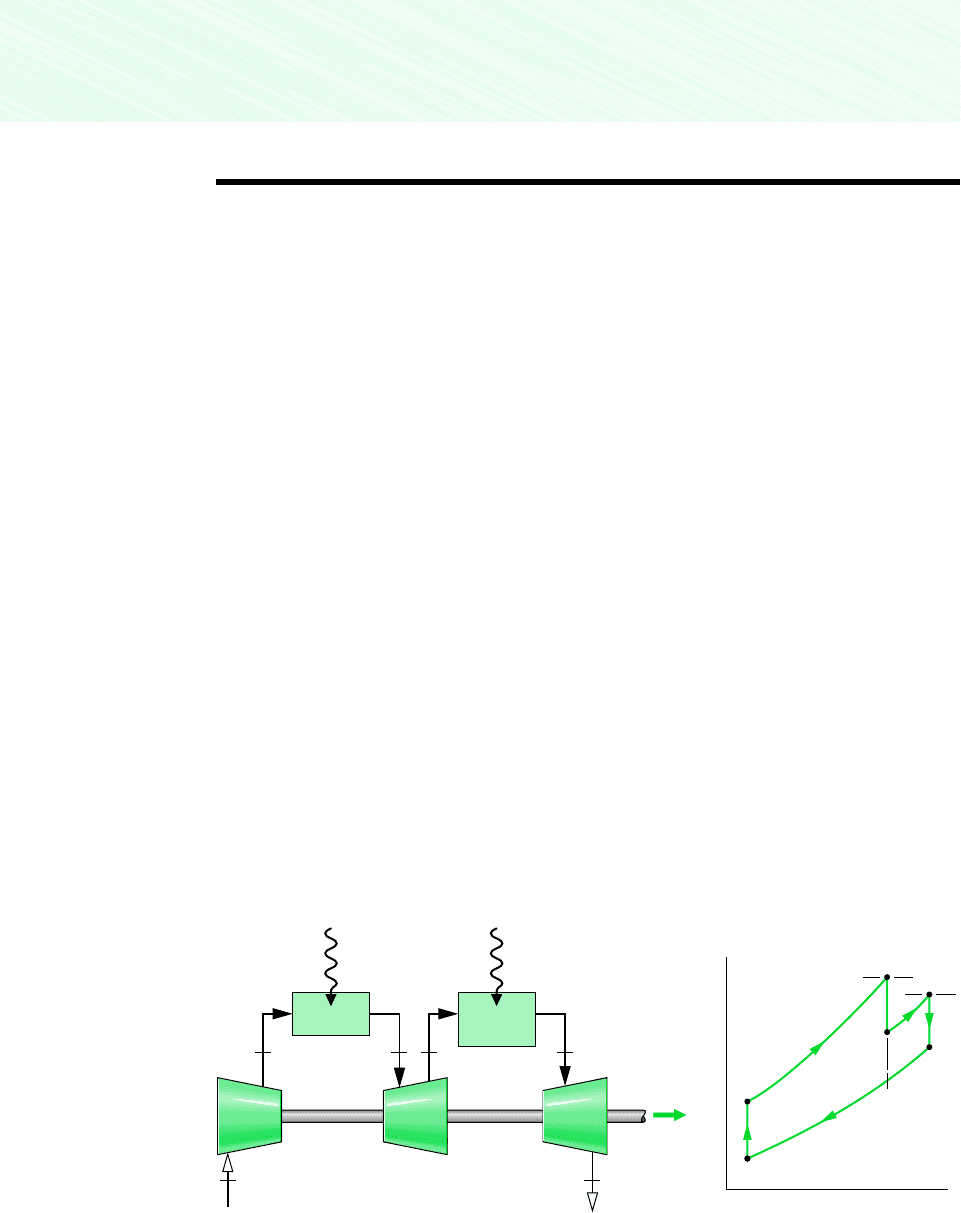
404 Chapter 9 Gas Power Systems

Two modifications of the basic gas turbine that increase the net work developed are multi-

stage expansion with reheat and multistage compression with intercooling. When used in

conjunction with regeneration, these modifications can result in substantial increases in ther-

mal efficiency. The concepts of reheat and intercooling are introduced in this section.

 9.8.1 Gas Turbines with Reheat

For metallurgical reasons, the temperature of the gaseous combustion products entering the tur-

bine must be limited. This temperature can be controlled by providing air in excess of the amount

required to burn the fuel in the combustor (see Chap. 13). As a consequence, the gases exiting

the combustor contain sufficient air to support the combustion of additional fuel. Some gas tur-

bine power plants take advantage of the excess air by means of a multistage turbine with a reheat

combustor between the stages. With this arrangement the net work per unit of mass flow can

be increased. Let us consider reheat from the vantage point of an air-standard analysis.

The basic features of a two-stage gas turbine with reheat are brought out by considering

an ideal air-standard Brayton cycle modified as shown in Fig. 9.16. After expansion from

state 3 to state a in the first turbine, the gas is reheated at constant pressure from state a to

state b. The expansion is then completed in the second turbine from state b to state 4. The

ideal Brayton cycle without reheat, 1–2–3–4–1, is shown on the same T–s diagram for com-

parison. Because lines of constant pressure on a T–s diagram diverge slightly with increas-

ing entropy, the total work of the two-stage turbine is greater than that of a single expansion

from state 3 to state 4. Thus, the net work for the reheat cycle is greater than that of the cy-

cle without reheat. Despite the increase in net work with reheat, the cycle thermal efficiency

would not necessarily increase because a greater total heat addition would be required. How-

ever, the temperature at the exit of the turbine is higher with reheat than without reheat, so

the potential for regeneration is enhanced.

Comparing the present thermal efficiency value with the one determined in Example 9.4, it should be evident that the ther-

mal efficiency can be increased significantly by means of regeneration.

The regenerator allows improved fuel utilization to be achieved by transferring a portion of the exergy in the hot turbine

exhaust gas to the cooler air flowing on the other side.

❷

❸



9.8 Regenerative Gas Turbines with

Reheat and Intercooling

Reheat

combustor

Turbine

stage 2

cycle

Combustor

Turbine

stage 1

Compressor

4′

a b

 Figure 9.16 Ideal gas turbine with reheat.

reheat

9.8 Regenerative Gas Turbines with Reheat and Intercooling 405

When reheat and regeneration are used together, the thermal efficiency can increase

significantly. The following example provides an illustration.

EXAMPLE 9.8 Brayton Cycle with Reheat and Regeneration

Consider a modification of the cycle of Example 9.4 involving reheat and regeneration. Air enters the compressor at 100 kPa,

300 K and is compressed to 1000 kPa. The temperature at the inlet to the first turbine stage is 1400 K. The expansion takes

place isentropically in two stages, with reheat to 1400 K between the stages at a constant pressure of 300 kPa. A regenerator

having an effectiveness of 100% is also incorporated in the cycle. Determine the thermal efficiency.

SOLUTION

Known: An ideal air-standard gas turbine cycle operates with reheat and regeneration. Temperatures and pressures at prin-

cipal states are specified.

Find: Determine the thermal efficiency.

Schematic and Given Data:

Regenerator

exit

= 300 K

p = 1000 kPa

p = 100 kPa

p = 300 kPa

= 1400 K

 Figure E9.8

Assumptions:

1. Each component of the power plant is analyzed as a control volume at

steady state.

2. The compressor and turbine processes are isentropic.

3. There are no pressure drops for flow through the heat exchangers.

4. The regenerator effectiveness is 100%.

5. Kinetic and potential energy effects are negligible.

6. The working fluid is air modeled as an ideal gas.

Analysis: We begin by determining the specific enthalpies at each principal state of the cycle. States 1, 2, and 3 are the

same as in Example 9.4: h

 300.19 kJ/kg, h

 579.9 kJ/kg, h

 1515.4 kJ/kg. The temperature at state b is the same as

at state 3, so h

 h

Since the first turbine process is isentropic, the enthalpy at state a can be determined using p

data from Table A-22 and

the relationship

Interpolating in Table A-22, we get h

 1095.9 kJ/kg.

The second turbine process is also isentropic, so the enthalpy at state 4 can be determined similarly. Thus

Interpolating in Table A-22, we obtain h

 1127.6 kJ/kg. Since the regenerator effectiveness is 100%, h

 h



1127.6 kJ/kg.

 p

 1450.52

100

300

 150.17

 p

 1450.52

300

1000

 135.15