Moran M.J., Shapiro H.N. Fundamentals of Engineering Thermodynamics

Подождите немного. Документ загружается.

386 Chapter 9 Gas Power Systems

CYCLE ANALYSIS.

Since the dual cycle is composed of the same types of processes as the

Otto and Diesel cycles, we can simply write down the appropriate work and heat transfer ex-

pressions by reference to the corresponding earlier developments. Thus, during the isentropic

compression process 1–2 there is no heat transfer, and the work is

As for the corresponding process of the Otto cycle, in the constant-volume portion of the

heat addition process, Process 2–3, there is no work, and the heat transfer is

In the constant-pressure portion of the heat addition process, Process 3–4, there is both work

and heat transfer, as for the corresponding process of the Diesel cycle

During the isentropic expansion process 4–5 there is no heat transfer, and the work is

Finally, the constant-volume heat rejection process 5–1 that completes the cycle involves

heat transfer but no work

The thermal efficiency is the ratio of the net work of the cycle to the total heat added

(9.14)

The example to follow provides an illustration of the analysis of an air-standard dual cycle.

The analysis exhibits many of the features found in the Otto and Diesel cycle examples

considered previously.

 1 

 u

2 1h

 h

h 

cycle



m  Q



 1 



m  Q



 u

 u

 u

 u

 p

 v

and

 h

 h

 u

 u

 u

 u

EXAMPLE 9.3 Analyzing the Dual Cycle

At the beginning of the compression process of an air-standard dual cycle with a compression ratio of 18, the temperature is

300 K and the pressure is 0.1 MPa. The pressure ratio for the constant volume part of the heating process is 1.5:1. The vol-

ume ratio for the constant pressure part of the heating process is 1.2:1. Determine (a) the thermal efficiency and (b) the mean

effective pressure, in MPa.

SOLUTION

Known: An air-standard dual cycle is executed in a piston–cylinder assembly. Conditions are known at the beginning of the

compression process, and necessary volume and pressure ratios are specified.

Find: Determine the thermal efficiency and the mep, in MPa.

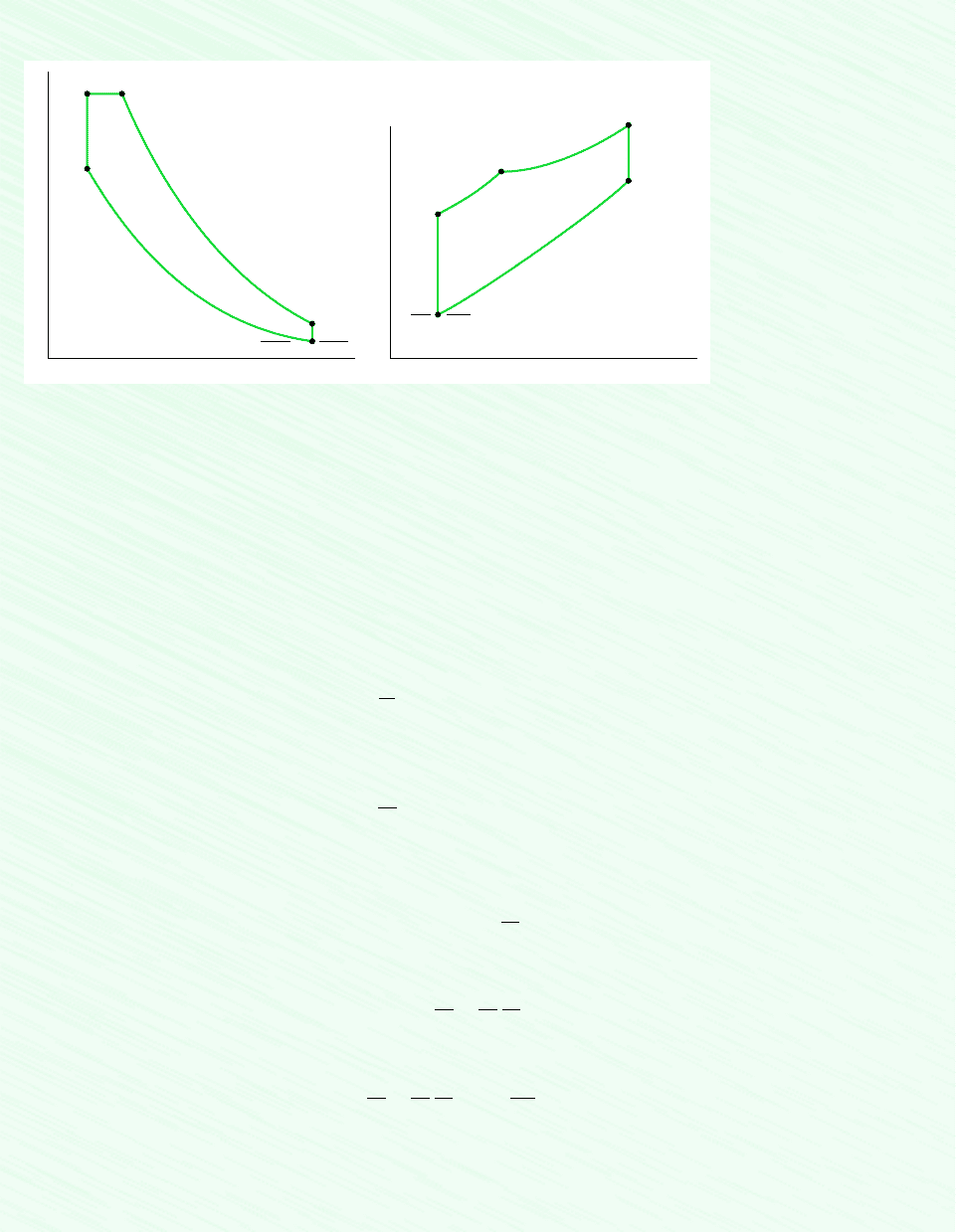
9.4 Air-Standard Dual Cycle 387

Schematic and Given Data:

p = c

= c

s = c

= 0.1 MPa

= 300 K

= 18

––

= 1.2

––

= 1.5,

––

 Figure E9.3

Assumptions:

1. The air in the piston–cylinder assembly is the closed system.

2. The compression and expansion processes are adiabatic.

3. All processes are internally reversible.

4. The air is modeled as an ideal gas.

5. Kinetic and potential energy effects are negligible.

Analysis: The analysis begins by determining properties at each principal state of the cycle. States 1 and 2 are the same as

in Example 9.2, so u

 214.07 kJ/kg, T

 898.3 K, u

 673.2 kJ/kg. Since Process 2–3 occurs at constant volume, the

ideal gas equation of state reduces to give

Interpolating in Table A-22, we get h

 1452.6 kJ/kg and u

 1065.8 kJ/kg.

Since Process 3–4 occurs at constant pressure, the ideal gas equation of state reduces to give

From Table A-22, h

 1778.3 kJ/kg and v

 5.609.

Process 4–5 is an isentropic expansion, so

The volume ratio V

V

required by this equation can be expressed as

With V

 V

, V

 V

, and given volume ratios

Inserting this in the above expression for v

Interpolating in Table A-22, we get u

 475.96 kJ/kg.

 15.60921152 84.135



 18 a

1.2

b 15



 v



 11.2211347.52 1617 K



 11.521898.32 1347.5 K

388 Chapter 9 Gas Power Systems

(a) The thermal efficiency is

(b) The mean effective pressure is

The net work of the cycle equals the net heat added, so

The specific volume at state 1 is evaluated in Example 9.2 as v

 0.861 m

/kg. Inserting values into the above expres-

sion for mep

mep 

311065.8  673.22 11778.3  1452.62 1475.96  214.0724 a

b `

1 kJ

` `

1 MPa

N/m

0.86111  1



182 m

/kg

 0.56 MPa

mep 

 u

2 1h

 h

2 1u

 u

11  1



mep 

cycle



 v



cycle



11  1



 0.635 163.5%2

 1 

1475.96  214.072

11065.8  673.22 11778.3  1452.62

h  1 



m  Q



 1 

 u

2 1h

 h

GAS TURBINE POWER PLANTS

This part of the chapter deals with gas turbine power plants. Gas turbines tend to be lighter

and more compact than the vapor power plants studied in Chap. 8. The favorable power-

output-to-weight ratio of gas turbines makes them well suited for transportation applications

(aircraft propulsion, marine power plants, and so on). Gas turbines are also commonly used

for stationary power generation.



9.5 Modeling Gas Turbine Power Plants

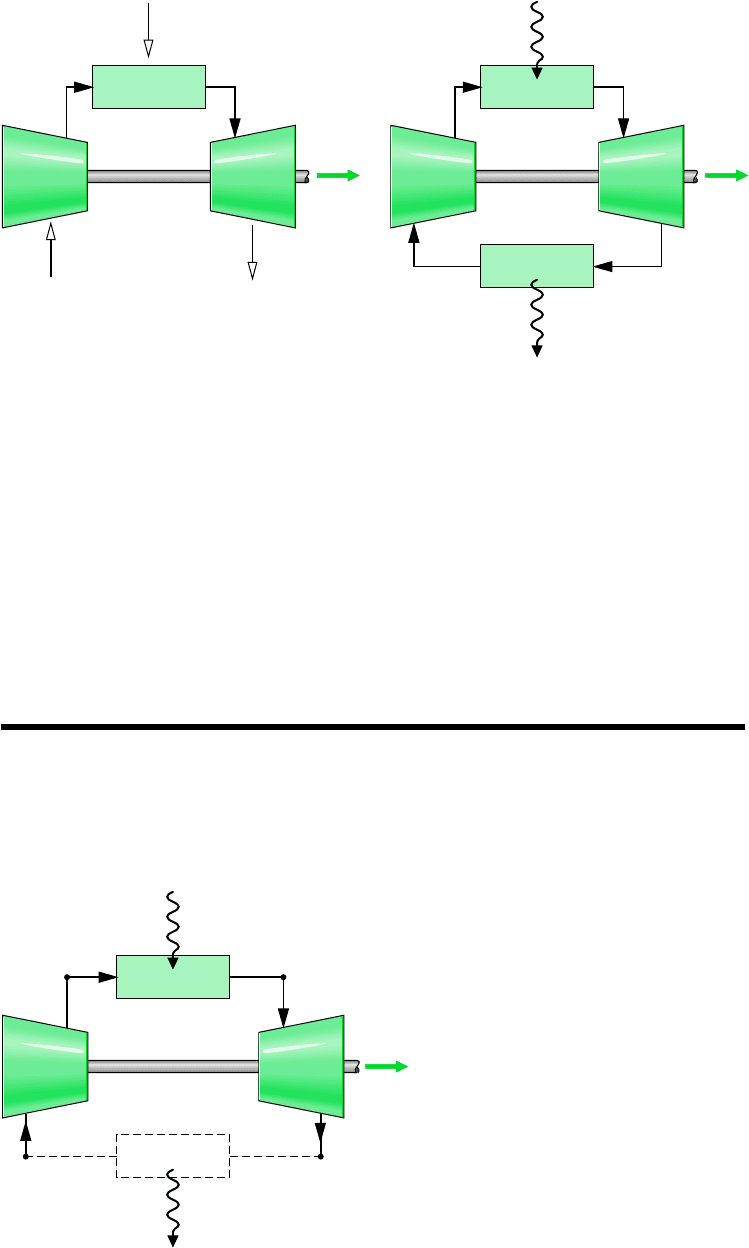
Gas turbine power plants may operate on either an open or closed basis. The open mode pic-

tured in Fig. 9.8a is more common. This is an engine in which atmospheric air is continuously

drawn into the compressor, where it is compressed to a high pressure. The air then enters a

combustion chamber, or combustor, where it is mixed with fuel and combustion occurs, re-

sulting in combustion products at an elevated temperature. The combustion products expand

through the turbine and are subsequently discharged to the surroundings. Part of the turbine

work developed is used to drive the compressor; the remainder is available to generate elec-

tricity, to propel a vehicle, or for other purposes. In the system pictured in Fig. 9.8b, the

working fluid receives an energy input by heat transfer from an external source, for example

a gas-cooled nuclear reactor. The gas exiting the turbine is passed through a heat exchanger,

where it is cooled prior to reentering the compressor.

An idealization often used in the study of open gas turbine power plants is that of an

air-standard analysis. In an air-standard analysis two assumptions are always made:

 The working fluid is air, which behaves as an ideal gas.

 The temperature rise that would be brought about by combustion is accomplished by a

heat transfer from an external source.

air-standard analysis:

gas turbines

9.6 Air-Standard Brayton Cycle 389

With an air-standard analysis, we avoid dealing with the complexities of the combustion

process and the change of composition during combustion. An air-standard analysis simplifies

the study of gas turbine power plants considerably. However, numerical values calculated on

this basis may provide only qualitative indications of power plant performance. Sufficient in-

formation about combustion and the properties of products of combustion is known (Chap. 13)

that the study of gas turbines can be conducted without the foregoing assumptions. Still, we

can learn some important aspects of gas turbine operation by proceeding on the basis of an

air-standard analysis, as follows.

Heat exchanger

Net

work

out

TurbineCompressor

out

Combustion

chamber

Fuel

Net

work

out

TurbineCompressor

Products

Air

(b)(a)

 Figure 9.8 Simple gas turbine. (a) Open to the atmosphere. (b) Closed.



9.6 Air-Standard Brayton Cycle

A schematic diagram of an air-standard gas turbine is shown in Fig. 9.9. The directions of

the principal energy transfers are indicated on this figure by arrows. In accordance with the

assumptions of an air-standard analysis, the temperature rise that would be achieved in the

Heat exchanger

TurbineCompressor

out

cycle

 Figure 9.9 Air-standard gas turbine

cycle.

390 Chapter 9 Gas Power Systems

combustion process is brought about by a heat transfer to the working fluid from an exter-

nal source and the working fluid is considered to be air as an ideal gas. With the air-standard

idealizations, air would be drawn into the compressor at state 1 from the surroundings and

later returned to the surroundings at state 4 with a temperature greater than the ambient tem-

perature. After interacting with the surroundings, each unit mass of discharged air would

eventually return to the same state as the air entering the compressor, so we may think of

the air passing through the components of the gas turbine as undergoing a thermodynamic

cycle. A simplified representation of the states visited by the air in such a cycle can be de-

vised by regarding the turbine exhaust air as restored to the compressor inlet state by pass-

ing through a heat exchanger where heat rejection to the surroundings occurs. The cycle that

results with this further idealization is called the air-standard Brayton cycle.

 9.6.1 Evaluating Principal Work and Heat Transfers

The following expressions for the work and heat transfers of energy that occur at steady state

are readily derived by reduction of the control volume mass and energy rate balances. These

energy transfers are positive in the directions of the arrows in Fig. 9.9. Assuming the turbine

operates adiabatically and with negligible effects of kinetic and potential energy, the work

developed per unit of mass is

(9.15)

where denotes the mass flow rate. With the same assumptions, the compressor work per

unit of mass is

(9.16)

The symbol denotes work input and takes on a positive value. The heat added to the cy-

cle per unit of mass is

(9.17)

The heat rejected per unit of mass is

(9.18)

where is positive in value.

The thermal efficiency of the cycle in Fig. 9.9 is

(9.19)

The back work ratio for the cycle is

(9.20)

For the same pressure rise, a gas turbine compressor would require a much greater work in-

put per unit of mass flow than the pump of a vapor power plant because the average specific

volume of the gas flowing through the compressor would be many times greater than that of

the liquid passing through the pump (see discussion of Eq. 6.53b in Sec. 6.9). Hence, a

relatively large portion of the work developed by the turbine is required to drive the

compressor. Typical back work ratios of gas turbines range from 40 to 80%. In comparison,

the back work ratios of vapor power plants are normally only 1 or 2%.

bwr 





 h

h 



 W





 h

2 1h

 h

out

 h

 h

 h

 h

 h

 h

 h

 h

Brayton cycle

9.6 Air-Standard Brayton Cycle 391

If the temperatures at the numbered states of the cycle are known, the specific enthalpies

required by the foregoing equations are readily obtained from the ideal gas table for air,

Table A-22. Alternatively, with the sacrifice of some accuracy, the variation of the specific

heats with temperature can be ignored and the specific heats taken as constant. The air-

standard analysis is then referred to as a cold air-standard analysis. As illustrated by the

discussion of internal combustion engines given previously, the chief advantage of the

assumption of constant specific heats is that simple expressions for quantities such as thermal

efficiency can be derived, and these can be used to deduce qualitative indications of cycle

performance without involving tabular data.

Since Eqs. 9.15 through 9.20 have been developed from mass and energy rate balances,

they apply equally when irreversibilities are present and in the absence of irreversibilities.

Although irreversibilities and losses associated with the various power plant components have

a pronounced effect on overall performance, it is instructive to consider an idealized cycle

in which they are assumed absent. Such a cycle establishes an upper limit on the perform-

ance of the air-standard Brayton cycle. This is considered next.

 9.6.2 Ideal Air-Standard Brayton Cycle

Ignoring irreversibilities as the air circulates through the various components of the Brayton

cycle, there are no frictional pressure drops, and the air flows at constant pressure through

the heat exchangers. If stray heat transfers to the surroundings are also ignored, the processes

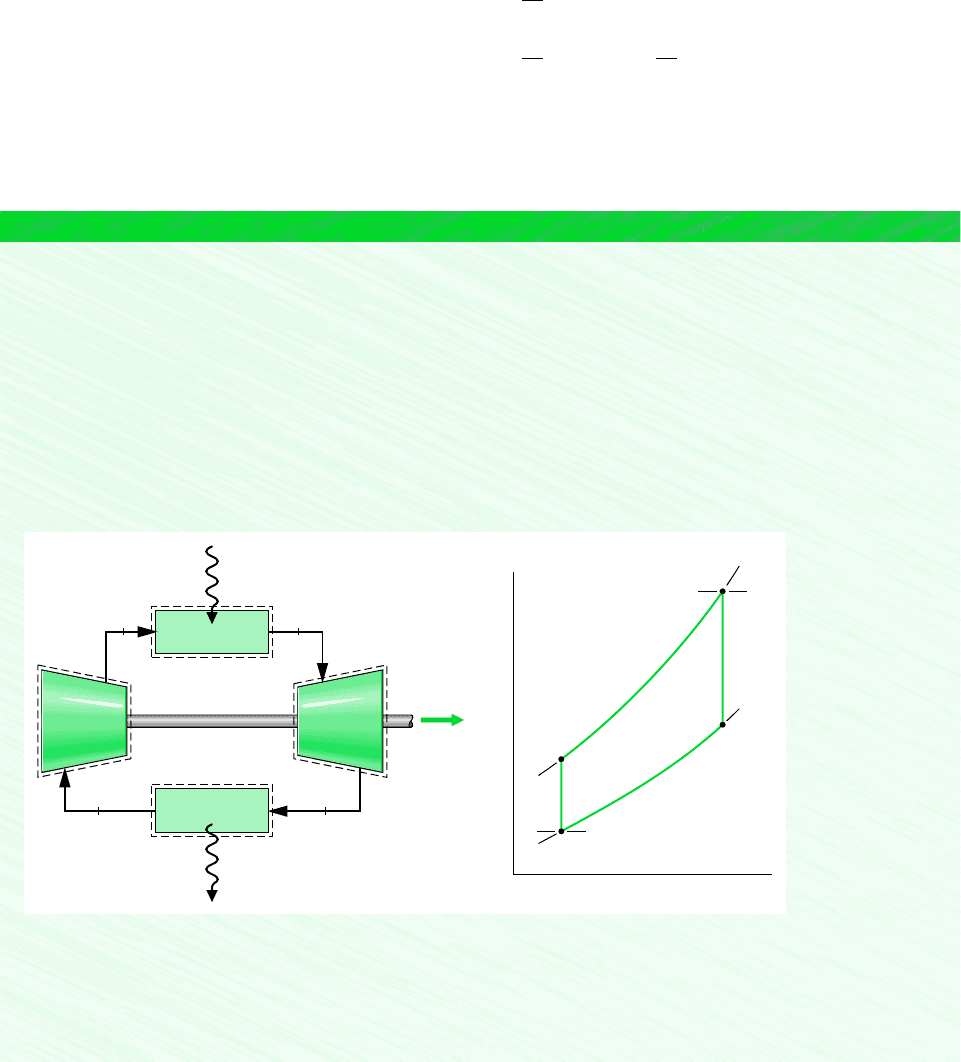
through the turbine and compressor are isentropic. The ideal cycle shown on the p–v and T–s

diagrams in Fig. 9.10 adheres to these idealizations.

Areas on the T–s and p–v diagrams of Fig. 9.10 can be interpreted as heat and work, re-

spectively, per unit of mass flowing. On the T–s diagram, area 2–3–a–b–2 represents the heat

added per unit of mass and area 1–4–a–b–1 is the heat rejected per unit of mass. On the p–v

diagram, area 1–2–a–b–1 represents the compressor work input per unit of mass and area

3–4–b–a–3 is the turbine work output per unit of mass (Sec. 6.9). The enclosed area on each

figure can be interpreted as the net work output or, equivalently, the net heat added.

When air table data are used to conduct an analysis involving the ideal Brayton cycle,

the following relationships, based on Eq. 6.43, apply for the isentropic processes 1–2

and 3–4

(9.21)

(9.22)

 p

2′

3′

p = c

s = c

 Figure 9.10 Air-standard ideal Brayton cycle.

392 Chapter 9 Gas Power Systems

Recall that p

is tabulated versus temperature in Tables A-22. Since the air flows through the

heat exchangers of the ideal cycle at constant pressure, it follows that p

p

 p

p

. This

relationship has been used in writing Eq. 9.22.

When an ideal Brayton cycle is analyzed on a cold air-standard basis, the specific heats

are taken as constant. Equations 9.21 and 9.22 are then replaced, respectively, by the fol-

lowing expressions, based on Eq. 6.45

(9.23)

(9.24)

where k is the specific heat ratio, k  c

c

In the next example, we illustrate the analysis of an ideal air-standard Brayton cycle and

compare results with those obtained on a cold air-standard basis.

 T

1k 12



 T

1k 12



 T

1k 12



EXAMPLE 9.4 Analyzing the Ideal Brayton Cycle

Air enters the compressor of an ideal air-standard Brayton cycle at 100 kPa, 300 K, with a volumetric flow rate of 5 m

/s.

The compressor pressure ratio is 10. The turbine inlet temperature is 1400 K. Determine (a) the thermal efficiency of the

cycle, (b) the back work ratio, (c) the net power developed, in kW.

SOLUTION

Known: An ideal air-standard Brayton cycle operates with given compressor inlet conditions, given turbine inlet tempera-

ture, and a known compressor pressure ratio.

Find: Determine the thermal efficiency, the back work ratio, and the net power developed, in kW.

Schematic and Given Data:

Heat exchanger

TurbineCompressor

cycle

out

= 100 kPa

= 300 K

= 1400 K = 10

––

= 300 K

p = 1000 kPa

p = 100 kPa

= 1400 K

 Figure E9.4

Assumptions:

1. Each component is analyzed as a control volume at steady state. The control volumes are shown on the accompanying

sketch by dashed lines.

2. The turbine and compressor processes are isentropic.

9.6 Air-Standard Brayton Cycle 393

3. There are no pressure drops for flow through the heat exchangers.

4. Kinetic and potential energy effects are negligible.

5. The working fluid is air modeled as an ideal gas.

Analysis: The analysis begins by determining the specific enthalpy at each numbered state of the cycle. At state 1, the tem-

perature is 300 K. From Table A-22, h

 300.19 kJ/kg and p

 1.386.

Since the compressor process is isentropic, the following relationship can be used to determine h

Then, interpolating in Table A-22, we obtain h

 579.9 kJ/kg.

The temperature at state 3 is given as T

 1400 K. With this temperature, the specific enthalpy at state 3 from Table A-22

is h

 1515.4 kJ/kg. Also, p

 450.5.

The specific enthalpy at state 4 is found by using the isentropic relation

Interpolating in Table A-22, we get h

 808.5 kJ/kg.

(a) The thermal efficiency is

(b) The back work ratio is

To evaluate the net power requires the mass flow rate which can be determined from the volumetric flow rate and specific

volume at the compressor inlet as follows

Since this becomes

Finally,

The use of the ideal gas table for air is featured in this solution. A solution also can be developed on a cold air-standard

basis in which constant specific heats are assumed. The details are left as an exercise, but for comparison the results are

cycle

 15.807 kg/s21706.9  279.72 a

b `

1 kW

1 kJ/s

` 2481 kW

 5.807 kg/s



1AV2



M2T



15 m

/s21100  10

N/m

8314

28.97

b 1300 K2

 1R



M2T





1AV2

cycle

 m

31h

 h

2 1h

 h

bwr 





 h



279.7

706.9

 0.396 139.6%2



706.9  279.7

935.5

 0.457 145.7%2



 h

2 1h

 h



11515.4  808.52 1579.9  300.192

1515.4  579.9

h 



2 1W



 p

 1450.5211



102 45.05



 110211.3862 13.86

❶

❷

❶

394 Chapter 9 Gas Power Systems

presented for the case k  1.4 in the following table:

Cold Air-Standard Analysis,

Parameter Air-Standard Analysis k  1.4

574.1 K 579.2 K

787.7 K 725.1 K

 0.457 0.482

bwr 0.396 0.414

2481 kW 2308 kW

The value of the back work ratio in the present gas turbine case is significantly greater than the back work ratio of the

simple vapor power cycle of Example 8.1.

cycle

❷

EFFECT OF PRESSURE RATIO ON PERFORMANCE. Conclusions that are qualitatively cor-

rect for actual gas turbines can be drawn from a study of the ideal Brayton cycle. The first

of these conclusions is that the thermal efficiency increases with increasing pressure ratio

across the compressor.  for example. . . referring again to the T–s diagram of Fig. 9.10,

we see that an increase in the pressure ratio changes the cycle from 1–2–3–4 –1 to

1–2–3–4–1. Since the average temperature of heat addition is greater in the latter cycle and

both cycles have the same heat rejection process, cycle 1–2–3–4–1 would have the greater

thermal efficiency. 

The increase in thermal efficiency with the pressure ratio across the compressor is also

brought out simply by the following development, in which the specific heat c

, and thus the

specific heat ratio k, is assumed constant. For constant c

, Eq. 9.19 becomes

Or, on further rearrangement

From Eqs. 9.23 and 9.24 above, T

T

 T

T

,so

Finally, introducing Eq. 9.23

(9.25)

By inspection of Eq. 9.25, it can be seen that the cold air-standard ideal Brayton cycle ther-

mal efficiency is a function of the pressure ratio across the compressor. This relationship is

shown in Fig. 9.11 for k  1.4.

There is a limit of about 1700 K imposed by metallurgical considerations on the maxi-

mum allowed temperature at the turbine inlet. It is instructive therefore to consider the ef-

fect of compressor pressure ratio on thermal efficiency when the turbine inlet temperature is

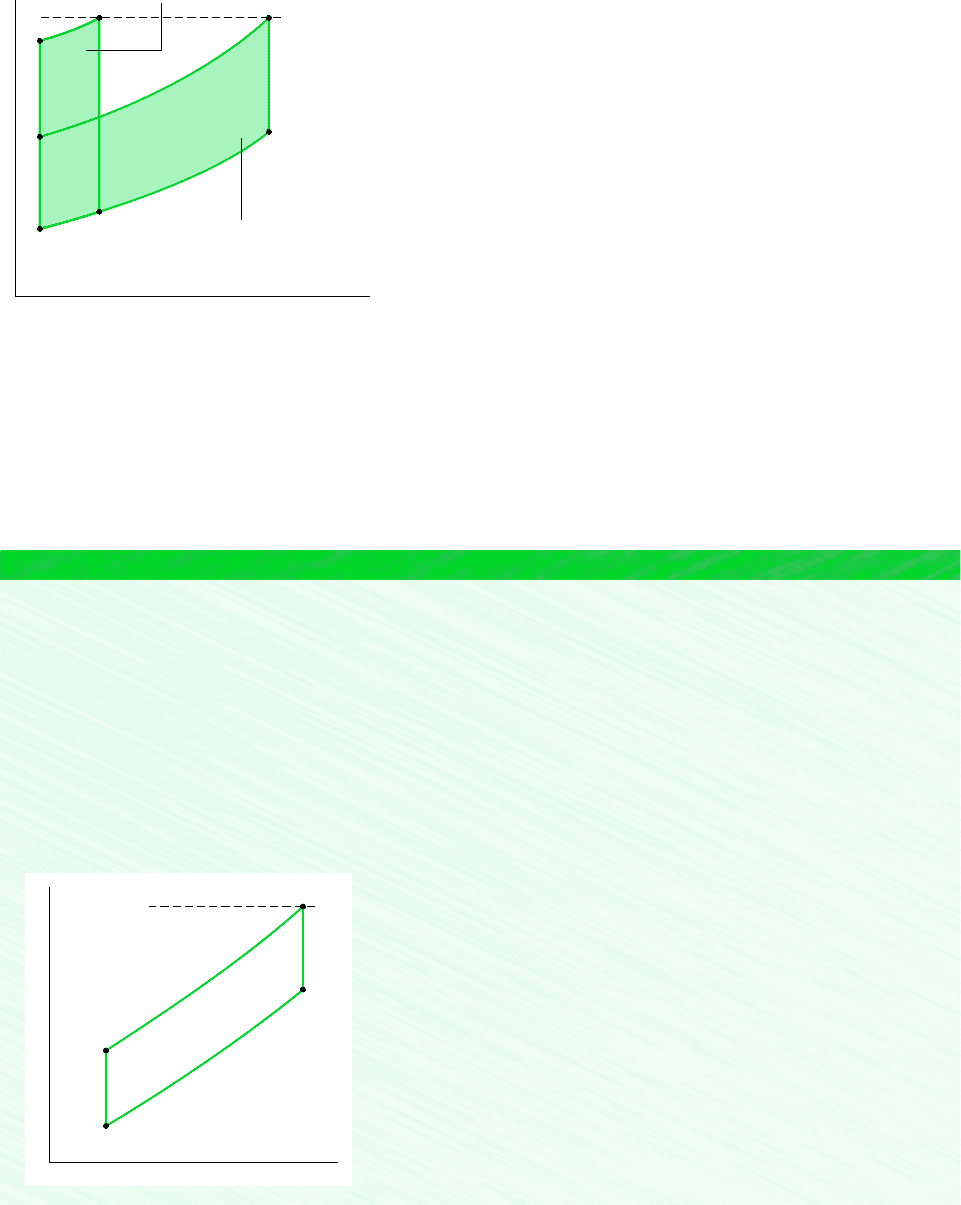
restricted to the maximum allowable temperature. The T–s diagrams of two ideal Brayton

cycles having the same turbine inlet temperature but different compressor pressure ratios are

shown in Fig. 9.12. Cycle A has a greater pressure ratio than cycle B and thus the greater

thermal efficiency. However, cycle B has a larger enclosed area and thus the greater net work

developed per unit of mass flow. Accordingly, for cycle A to develop the same net power

h  1 



1k 12



1k constant2

h  1 



 1



 1

h 

 T

2 c

 T

 1 

 T

2468100

Compressor pressure ratio

η(%)

 Figure 9.11 Ideal

Brayton cycle thermal

efficiency versus com-

pressor pressure ratio,

k  1.4.

9.6 Air-Standard Brayton Cycle 395

output as cycle B, a larger mass flow rate would be required, and this might dictate a larger

system. These considerations are important for gas turbines intended for use in vehicles where

engine weight must be kept small. For such applications, it is desirable to operate near the

compressor pressure ratio that yields the most work per unit of mass flow and not the pres-

sure ratio for the greatest thermal efficiency.

Example 9.5 provides an illustration of the determination of the compressor pressure ra-

tio for maximum net work per unit of mass flow for the cold air-standard Brayton cycle.

Cycle B: 1-2-3-4-1

larger net work per unit of mass flow

Cycle A: 1-2′-3′-4′-1

larger thermal efficiency

Turbine inlet

temperature

33′

2′

4′

 Figure 9.12 Ideal Brayton cycles with

different pressure ratios and the same turbine

inlet temperature.

EXAMPLE 9.5 Compressor Pressure Ratio for Maximum Net Work

Determine the pressure ratio across the compressor of an ideal Brayton cycle for the maximum net work output per unit of

mass flow if the state at the compressor inlet and the temperature at the turbine inlet are fixed. Use a cold air-standard analysis

and ignore kinetic and potential energy effects. Discuss.

SOLUTION

Known: An ideal Brayton cycle operates with a specified state at the inlet to the compressor and a specified turbine inlet

temperature.

Find: Determine the pressure ratio across the compressor for the maximum net work output per unit of mass flow, and dis-

cuss the result.

Schematic and Given Data:

Compressor inlet state fixed

Turbine inlet

temperature fixed

variable

––

 Figure E9.5

Assumptions:

1. Each component is analyzed as a control volume at steady state.

2. The turbine and compressor processes are isentropic.

3. There are no pressure drops for flow through the heat exchangers.

4. Kinetic and potential energy effects are negligible.

5. The working fluid is air modeled as an ideal gas.

6. The specific heat c

and the specific heat ratio k are constant.