Moran M.J., Shapiro H.N. Fundamentals of Engineering Thermodynamics

Подождите немного. Документ загружается.

 1000 K and p

 3 bar. Using Eq. 6.21a and data from Table A-22



If a table giving s (or ) is not available for a particular gas of interest, the integrals of

Eqs. 6.18 and 6.19 can be performed analytically or numerically using specific heat data such

as provided in Tables A-20 and A-21.

ASSUMING CONSTANT SPECIFIC HEATS. When the specific heats c

and c

are taken as

constants, Eqs. 6.18 and 6.19 reduce, respectively, to

(6.22)

(6.23)

These equations, along with Eqs. 3.50 and 3.51 giving u and h, respectively, are applica-

ble when assuming the ideal gas model with constant specific heats.

 for example. . . let us determine the change in specific entropy, in of air

as an ideal gas undergoing a process from T

 300 K, p

 1 bar to T

 400 K, p

 5 bar.

Because of the relatively small temperature range, we assume a constant value of c

evaluated

at 350 K. Using Eq. 6.23 and c

 1.008 from Table A-20



COMPUTER RETRIEVAL. For air and other gases modeled as ideal gases, IT directly returns

s(T, p) based upon the following form of Eq. 6.19

and the following choice of reference state and reference value: T

ref

 0 K (0R), p

ref



1 atm, and s(T

ref

, p

ref

)  0, giving

Changes in specific entropy evaluated using IT agree with entropy changes evaluated

using ideal gas tables.

 for example. . . consider a process of air as an ideal gas from

 300 K, p

 1 bar to T

 1000 K, p

 3 bar. The change in specific entropy, denoted

s1T, p2



1T 2

dT  R ln

ref

s1T, p2 s1T

ref

, p

ref

2



ref

1T 2

dT  R ln

ref

0.1719 kJ/kg

 a1.008

b ln a

400 K

300 K

b a

8.314

28.97

b ln a

5 bar

1 bar

¢s  c

 R ln

kJ/kg

s1T

, p

2 s1T

, p

2 c

 R ln

s1T

, v

2 s1T

, v

2 c

 R ln

s °

 0.9504 kJ/kg

 12.96770  1.702032



8.314

28.97

3 bar

1 bar

 s

 s°1T

2 s°1T

2 R ln

216 Chapter 6 Using Entropy



6.4 Entropy Change in Internally Reversible Processes 217

as dels, is determined in SI units using IT as follows:

p1 = 1 // bar

T1 = 300 // K

p2 = 3

T2 = 1000

s1 = s_TP(“Air”,T1,p1)

s2 = s_TP(“Air”,T2,p2)

dels = s2 – s1

The software returns values of s

 1.706, s

 2.656, and dels  0.9501, all in units of

This value for s agrees with the value obtained using Table A-22 in the example

following Eqs. 6.21.  Note that IT returns specific entropy directly and does not use the

special function s.

 6.3.3 Entropy Change of an Incompressible Substance

The incompressible substance model introduced in Sec. 3.3.6 assumes that the specific vol-

ume (density) is constant and the specific heat depends solely on temperature, c

 c(T). Ac-

cordingly, the differential change in specific internal energy is du  c(T ) dT and Eq. 6.15

reduces to

On integration, the change in specific entropy is

When the specific heat is assumed constant, this becomes

(6.24)

Equation 6.24, along with Eqs. 3.20 giving u and h, respectively, are applicable to liquids

and solids modeled as incompressible. Specific heats of some common liquids and solids are

given in Table A-19.

 s

 c ln

1incompressible, constant c2

 s





c1T

1incompressible2

ds 

c1T

2 dT



p dv



c1T 2 dT

kJ/kg



6.4 Entropy Change in Internally

Reversible Processes

In this section the relationship between entropy change and heat transfer for internally re-

versible processes is considered. The concepts introduced have important applications in sub-

sequent sections of the book. The present discussion is limited to the case of closed systems.

Similar considerations for control volumes are presented in Sec. 6.9.

As a closed system undergoes an internally reversible process, its entropy can increase,

decrease, or remain constant. This can be brought out using Eq. 6.4b

dS  a

rev

int



which indicates that when a closed system undergoing an internally reversible process receives

energy by heat transfer, the system experiences an increase in entropy. Conversely, when en-

ergy is removed from the system by heat transfer, the entropy of the system decreases. This

can be interpreted to mean that an entropy transfer accompanies heat transfer. The direction

of the entropy transfer is the same as that of the heat transfer. In an adiabatic internally

reversible process, the entropy would remain constant. A constant-entropy process is called

an isentropic process.

On rearrangement, the above expression gives

Integrating from an initial state 1 to a final state 2

(6.25)

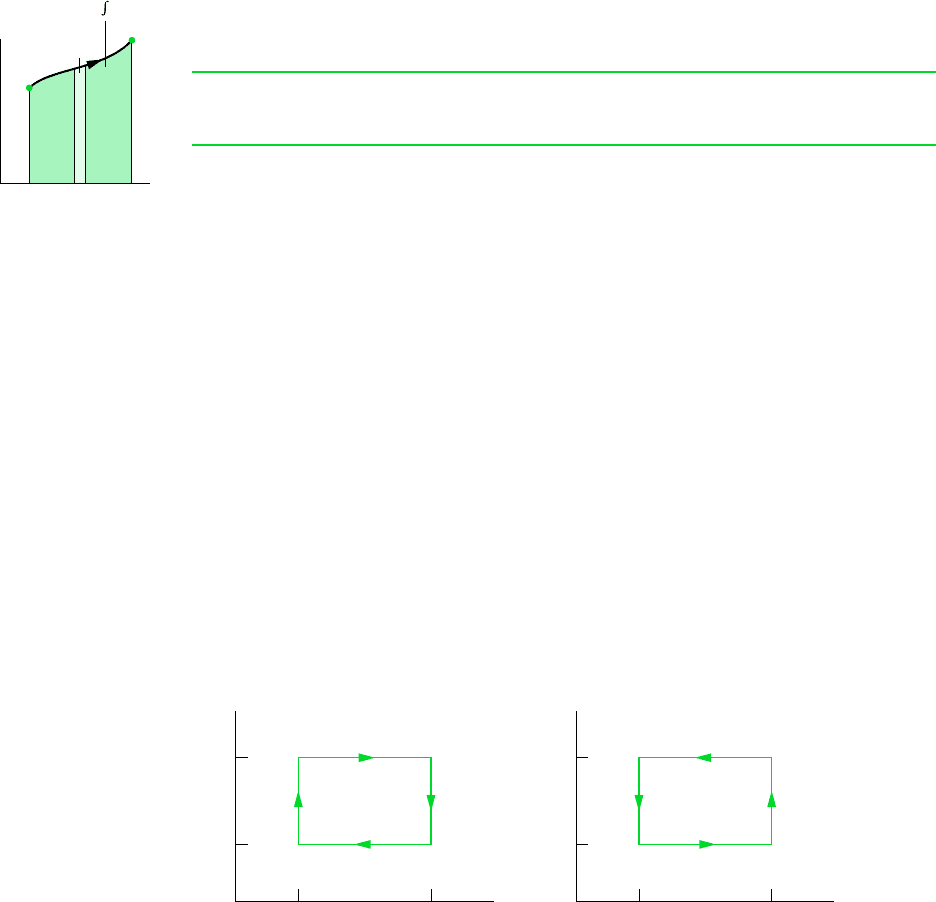
From Eq. 6.25 it can be concluded that an energy transfer by heat to a closed system dur-

ing an internally reversible process can be represented as an area on a temperature–entropy

diagram. Figure 6.5 illustrates the area interpretation of heat transfer for an arbitrary inter-

nally reversible process in which temperature varies. Carefully note that temperature must

be in kelvins or degrees Rankine, and the area is the entire area under the curve (shown

shaded). Also note that the area interpretation of heat transfer is not valid for irreversible

processes, as will be demonstrated later.

To provide an example illustrating both the entropy change that accompanies heat transfer

and the area interpretation of heat transfer, consider Fig. 6.6a, which shows a Carnot power

cycle (Sec. 5.6). The cycle consists of four internally reversible processes in series: two

isothermal processes alternated with two adiabatic processes. In Process 2–3, heat transfer

to the system occurs while the temperature of the system remains constant at T

. The sys-

tem entropy increases due to the accompanying entropy transfer. For this process, Eq. 6.25

gives Q

 T

 S

), so area 2–3–a–b–2 on Fig. 6.6a represents the heat transfer during

the process. Process 3–4 is an adiabatic and internally reversible process and thus is an isen-

tropic (constant-entropy) process. Process 4–1 is an isothermal process at T

during which

heat is transferred from the system. Since entropy transfer accompanies the heat transfer, sys-

tem entropy decreases. For this process, Eq. 6.25 gives Q

 T

 S

), which is nega-

tive in value. Area 4–1–b–a–4 on Fig. 6.6a represents the magnitude of the heat transfer Q

Process 1–2, which completes the cycle, is adiabatic and internally reversible (isentropic).

int

rev





T dS

1dQ2

int

rev

 T dS

218 Chapter 6 Using Entropy

(δQ) = T dS

Q =

T dS

int

rev

int

rev

 Figure 6.6 Carnot cycles on the temperature–entropy diagram. (a) Power

cycle. (b) Refrigeration or heat pump cycle.

 Figure 6.5 Area

representation of heat

transfer for an internally

reversible process of a

closed system.

isentropic process

Carnot cycle



(a)(b)

6.4 Entropy Change in Internally Reversible Processes 219

The net work of any cycle is equal to the net heat transfer, so enclosed area 1–2–3–4–1

represents the net work of the cycle. The thermal efficiency of the cycle may also be ex-

pressed in terms of areas:

The numerator of this expression is (T

 T

)(S

 S

) and the denominator is T

 S

so the thermal efficiency can be given in terms of temperatures only as   1  T

T

. If

the cycle were executed as shown in Fig. 6.6b, the result would be a Carnot refrigeration or

heat pump cycle. In such a cycle, heat is transferred to the system while its temperature re-

mains at T

, so entropy increases during Process 1–2. In Process 3–4 heat is transferred from

the system while the temperature remains constant at T

and entropy decreases.

To further illustrate concepts introduced in this section, the next example considers water

undergoing an internally reversible process while contained in a piston–cylinder assembly.

h 

cycle



area 1–2–3–4–1

area 2–3–a–b–2

EXAMPLE 6.1 Internally Reversible Process of Water

Water, initially a saturated liquid at 100C, is contained in a piston–cylinder assembly. The water undergoes a process to the

corresponding saturated vapor state, during which the piston moves freely in the cylinder. If the change of state is brought

about by heating the water as it undergoes an internally reversible process at constant pressure and temperature, determine the

work and heat transfer per unit of mass, each in kJ/kg.

SOLUTION

Known: Water contained in a piston–cylinder assembly undergoes an internally reversible process at 100C from saturated

liquid to saturated vapor.

Find: Determine the work and heat transfer per unit mass.

Schematic and Given Data:

100°C

––

System boundary

Water

 Figure E6.1

Assumptions:

1. The water in the piston–cylinder assembly is a closed system.

2. The process is internally reversible.

3. Temperature and pressure are constant during the process.

4. There is no change in kinetic or potential energy between the two end states.

In this section, the Clausius inequality expressed by Eq. 6.2 and the defining equation for

entropy change are used to develop the entropy balance for closed systems. The entropy bal-

ance is an expression of the second law that is particularly convenient for thermodynamic

analysis. The current presentation is limited to closed systems. The entropy balance is ex-

tended to control volumes in Sec. 6.6.

 6.5.1 Developing the Entropy Balance

Shown in Fig. 6.7 is a cycle executed by a closed system. The cycle consists of process I,

during which internal irreversibilities are present, followed by internally reversible process

R. For this cycle, Eq. 6.2 takes the form

(6.26)







rev

int

s

220 Chapter 6 Using Entropy



6.5 Entropy Balance for Closed Systems

❶

Analysis: At constant pressure the work is

With values from Table A-2

Since the process is internally reversible and at constant temperature, Eq. 6.25 gives

With values from Table A-2

As shown in the accompanying figure, the work and heat transfer can be represented as areas on p–v and T–s diagrams,

respectively.

The heat transfer can be evaluated alternatively from an energy balance written on a unit mass basis as

Introducing Wm  p(v

 v

) and solving

From Table A-2 at 100C, h

 h

 2257 kJ/kg, which is the same value for Qm as obtained in the solution.

 h

 h

 1u

 pv

2 1u

 pv

 1u

 u

2 p1v

 v

 u





 1373.15 K217.3549  1.30692 kJ/kg

K  2257 kJ/kg

 T 1s

 s

Q 



T dS  m



T ds

 170 kJ/kg

 11.014

bar2 11.673  1.0435  10

3

2 a

N/m

1 bar





p dv  p1v

 v

 Figure 6.7 Cycle

used to develop the

entropy balance.

❶

6.5 Entropy Balance for Closed Systems 221

where the first integral is for process I and the second is for process R. The subscript b in the

first integral serves as a reminder that the integrand is evaluated at the system boundary. The sub-

script is not required in the second integral because temperature is uniform throughout the system

at each intermediate state of an internally reversible process. Since no irreversibilities are

associated with process R, the term 

cycle

of Eq. 6.2, which accounts for the effect of

irreversibilities during the cycle, refers only to process I and is shown in Eq. 6.26 simply as .

Applying the definition of entropy change, we can express the second integral of Eq. 6.26 as

With this, Eq. 6.26 becomes

Finally, on rearranging the last equation, the closed system entropy balance results

(6.27)

entropy entropy entropy

change transfer production

If the end states are fixed, the entropy change on the left side of Eq. 6.27 can be evaluated

independently of the details of the process. However, the two terms on the right side depend

explicitly on the nature of the process and cannot be determined solely from knowledge of

the end states. The first term on the right side of Eq. 6.27 is associated with heat transfer to

or from the system during the process. This term can be interpreted as the entropy transfer

accompanying heat transfer. The direction of entropy transfer is the same as the direction of

the heat transfer, and the same sign convention applies as for heat transfer: A positive value

means that entropy is transferred into the system, and a negative value means that entropy is

transferred out. When there is no heat transfer, there is no entropy transfer.

The entropy change of a system is not accounted for solely by the entropy transfer, but is

due in part to the second term on the right side of Eq. 6.27 denoted by . The term  is pos-

itive when internal irreversibilities are present during the process and vanishes when no in-

ternal irreversibilities are present. This can be described by saying that entropy is produced

within the system by the action of irreversibilities. The second law of thermodynamics can

be interpreted as requiring that entropy is produced by irreversibilities and conserved only

in the limit as irreversibilities are reduced to zero. Since  measures the effect of irre-

versibilities present within the system during a process, its value depends on the nature of

the process and not solely on the end states. It is not a property.

When applying the entropy balance to a closed system, it is essential to remember the re-

quirements imposed by the second law on entropy production: The second law requires that

entropy production be positive, or zero, in value

(6.28)

The value of the entropy production cannot be negative. By contrast, the change in entropy

of the system may be positive, negative, or zero:

(6.29)

Like other properties, entropy change can be determined without knowledge of the details

of the process.

 S

: •

7 0

 0

6 0

s: e

7 0

 0

irreversibilities present within the system

no irreversibilities present within the system

 S









 1S

 S

2s

 S





rev

int

closed system entropy

balance

entropy transfer

accompanying heat

transfer

entropy production



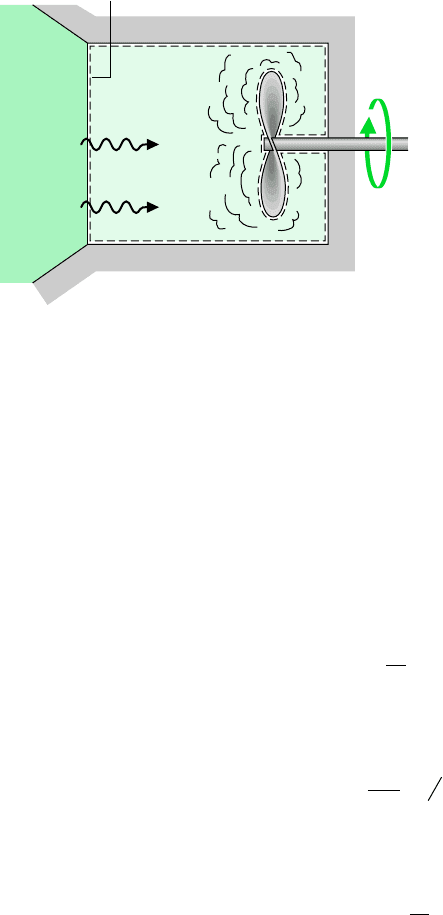
 for example. . . to illustrate the entropy transfer and entropy production concepts,

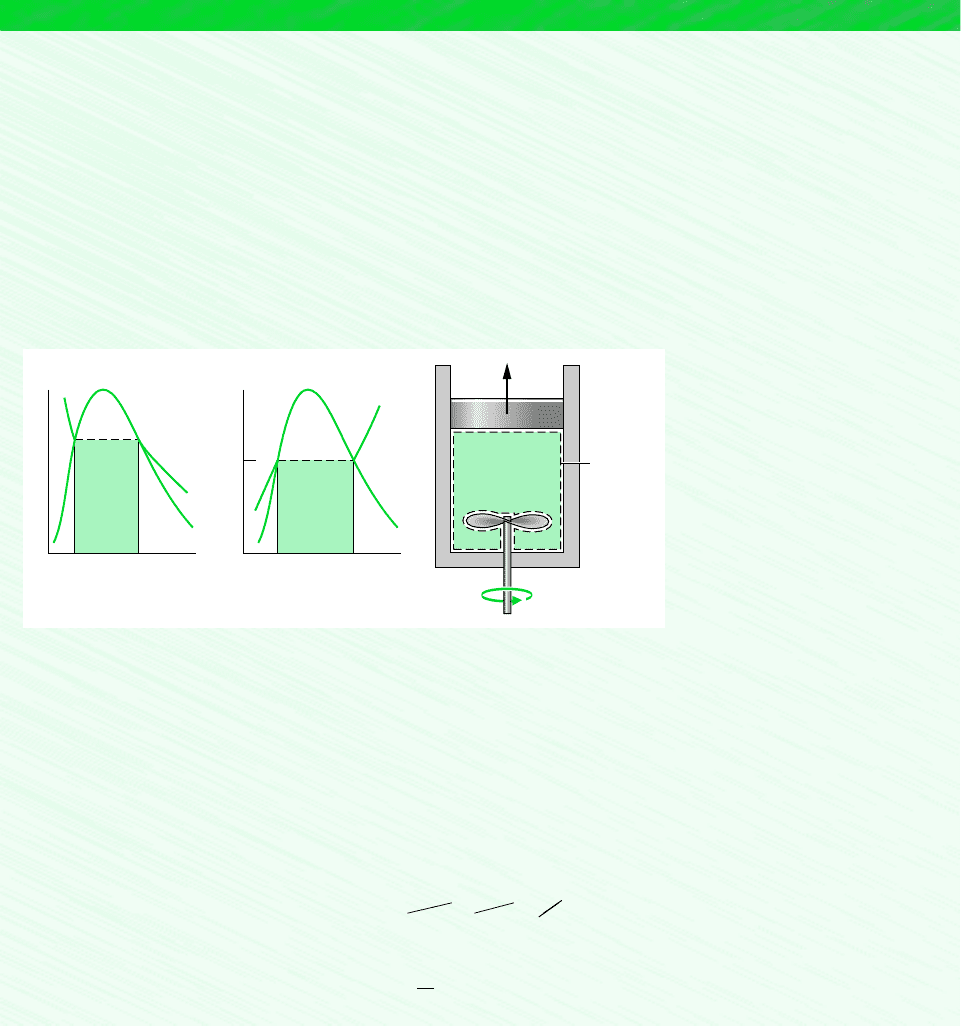
as well as the accounting nature of entropy balance, consider Fig. 6.8. The figure shows a

system consisting of a gas or liquid in a rigid container stirred by a paddle wheel while re-

ceiving a heat transfer Q from a reservoir. The temperature at the portion of the boundary

where heat transfer occurs is the same as the constant temperature of the reservoir, T

. By

definition, the reservoir is free of irreversibilities; however, the system is not without irre-

versibilities, for fluid friction is evidently present, and there may be other irreversibilities

within the system.

Let us now apply the entropy balance to the system and to the reservoir. Since T

is con-

stant, the integral in Eq. 6.27 is readily evaluated, and the entropy balance for the system

reduces to

(6.30)

where QT

accounts for entropy transfer into the system accompanying heat transfer Q. The

entropy balance for the reservoir takes the form

where the entropy production term is set equal to zero because the reservoir is without irre-

versibilities. Since Q

res

Q, the last equation becomes

The minus sign signals that entropy is carried out of the reservoir accompanying heat transfer.

Hence, the entropy of the reservoir decreases by an amount equal to the entropy transferred from

it to the system. However, as shown by Eq. 6.30, the entropy change of the system exceeds the

amount of entropy transferred to it because of entropy production within the system.



If the heat transfer were oppositely directed in the above example, passing instead from

the system to the reservoir, the magnitude of the entropy transfer would remain the same,

but its direction would be reversed. In such a case, the entropy of the system would decrease

if the amount of entropy transferred from the system to the reservoir exceeded the amount

of entropy produced within the system due to irreversibilities. Finally, observe that there is

no entropy transfer associated with work.

¢S 4

res



¢S 4

res



res

 s

res

 S



 s

222 Chapter 6 Using Entropy

Gas or liquid

Reservoir

at T

Q/T

This portion of the

boundary is at temperature T

 Figure 6.8 Illustration of the

entropy transfer and entropy production

concepts.

6.5 Entropy Balance for Closed Systems 223

 6.5.2 Other Forms of the Entropy Balance

The entropy balance can be expressed in various forms convenient for particular analyses.

For example, if heat transfer takes place at several locations on the boundary of a system

where the temperatures do not vary with position or time, the entropy transfer term can be

expressed as a sum, so Eq. 6.27 takes the form

(6.31)

where Q

T

is the amount of entropy transferred through the portion of the boundary at tem-

perature T

On a time rate basis, the closed system entropy rate balance is

(6.32)

where dSdt is the time rate of change of entropy of the system. The term represents

the time rate of entropy transfer through the portion of the boundary whose instantaneous

temperature is T

. The term accounts for the time rate of entropy production due to irre-

versibilities within the system.

It is sometimes convenient to use the entropy balance expressed in differential form

(6.33)

Note that the differentials of the nonproperties Q and  are shown, respectively, as Q and .

When there are no internal irreversibilities,  vanishes and Eq. 6.33 reduces to Eq. 6.4b.

 6.5.3 Evaluating Entropy Production and Transfer

Regardless of the form taken by the entropy balance, the objective in many applications is

to evaluate the entropy production term. However, the value of the entropy production for a

given process of a system often does not have much significance by itself. The significance

is normally determined through comparison. For example, the entropy production within a

given component might be compared to the entropy production values of the other compo-

nents included in an overall system formed by these components. By comparing entropy pro-

duction values, the components where appreciable irreversibilities occur can be identified

and rank ordered. This allows attention to be focused on the components that contribute most

to inefficient operation of the overall system.

To evaluate the entropy transfer term of the entropy balance requires information re-

garding both the heat transfer and the temperature on the boundary where the heat transfer

occurs. The entropy transfer term is not always subject to direct evaluation, however, be-

cause the required information is either unknown or not defined, such as when the system

passes through states sufficiently far from equilibrium. In such applications, it may be con-

venient, therefore, to enlarge the system to include enough of the immediate surroundings

that the temperature on the boundary of the enlarged system corresponds to the tempera-

ture of the surroundings away from the immediate vicinity of the system, T

. The entropy

transfer term is then simply QT

. However, as the irreversibilities present would not be just

for the system of interest but for the enlarged system, the entropy production term would

account for the effects of internal irreversibilities within the original system and external

irreversibilities present within that portion of the surroundings included within the enlarged

system.

dS  a

 ds





 s

 S



 s

T > T

Temperature

variation

Boundary of

enlarged system

closed system entropy

rate balance



224 Chapter 6 Using Entropy

EXAMPLE 6.2 Irreversible Process of Water

Water initially a saturated liquid at 100C is contained within a piston–cylinder assembly. The water undergoes a process to

the corresponding saturated vapor state, during which the piston moves freely in the cylinder. There is no heat transfer with

the surroundings. If the change of state is brought about by the action of a paddle wheel, determine the net work per unit

mass, in kJ/kg, and the amount of entropy produced per unit mass, in

SOLUTION

Known: Water contained in a piston–cylinder assembly undergoes an adiabatic process from saturated liquid to saturated

vapor at 100C. During the process, the piston moves freely, and the water is rapidly stirred by a paddle wheel.

Find: Determine the net work per unit mass and the entropy produced per unit mass.

Schematic and Given Data:

kJ/kg

100°C

Area is

not work

Area is

not heat

Water

System

boundary

 Figure E6.2

Assumptions:

1. The water in the piston–cylinder assembly is a closed system.

2. There is no heat transfer with the surroundings.

3. The system is at an equilibrium state initially and finally. There is no change in kinetic or potential energy between these

two states.

Analysis: As the volume of the system increases during the process, there is an energy transfer by work from the system

during the expansion, as well as an energy transfer by work to the system via the paddle wheel. The net work can be evalu-

ated from an energy balance, which reduces with assumptions 2 and 3 to

On a unit mass basis, the energy balance reduces to

1u

 u

¢U  ¢KE

 ¢PE

 Q

 W

 6.5.4 Illustrations

The following examples illustrate the use of the energy and entropy balances for the analy-

sis of closed systems. Property relations and property diagrams also contribute significantly

in developing solutions. The first example reconsiders the system and end states of Exam-

ple 6.1 to demonstrate that entropy is produced when internal irreversibilities are present and

that the amount of entropy production is not a property.

❶

6.5 Entropy Balance for Closed Systems 225

As an illustration of second law reasoning, the next example uses the fact that the entropy

production term of the entropy balance cannot be negative.

With specific internal energy values from Table A-2 at 100C

The minus sign indicates that the work input by stirring is greater in magnitude than the work done by the water as it

expands.

The amount of entropy produced is evaluated by applying an entropy balance. Since there is no heat transfer, the term

accounting for entropy transfer vanishes

On a unit mass basis, this becomes on rearrangement

With specific entropy values from Table A-2 at 100C

Although each end state is an equilibrium state at the same pressure and temperature, the pressure and temperature are not

necessarily uniform throughout the system at intervening states, nor are they necessarily constant in value during the

process. Accordingly, there is no well-defined “path” for the process. This is emphasized by the use of dashed lines to

represent the process on these p–v and T–s diagrams. The dashed lines indicate only that a process has taken place, and

no “area” should be associated with them. In particular, note that the process is adiabatic, so the “area” below the dashed

line on the T–s diagram can have no significance as heat transfer. Similarly, the work cannot be associated with an area

on the p–v diagram.

The change of state is the same in the present example as in Example 6.1. However, in Example 6.1 the change of state

is brought about by heat transfer while the system undergoes an internally reversible process. Accordingly, the value of

entropy production for the process of Example 6.1 is zero. Here, fluid friction is present during the process and the en-

tropy production is positive in value. Accordingly, different values of entropy production are obtained for two processes

between the same end states. This demonstrates that entropy production is not a property.

 6.048

 s

 s

¢S 



 s

2087.56

❶

❷

EXAMPLE 6.3 Evaluating Minimum Theoretical Compression Work

Refrigerant 134a is compressed adiabatically in a piston–cylinder assembly from saturated vapor at 0C to a final pressure of

0.7 MPa. Determine the minimum theoretical work input required per unit mass of refrigerant, in kJ/kg.

SOLUTION

Known: Refrigerant 134a is compressed without heat transfer from a specified initial state to a specified final pressure.

Find: Determine the minimum theoretical work input required per unit of mass.