Moran M.J., Shapiro H.N. Fundamentals of Engineering Thermodynamics

Подождите немного. Документ загружается.

186 Chapter 5 The Second Law of Thermodynamics

efficiency of the cycle is

(5.2)

where Q

is the amount of energy received by the system from the hot reservoir by heat

transfer and Q

is the amount of energy discharged from the system to the cold reservoir by

heat transfer.

If the value of Q

were zero, the system of Fig. 5.5 would withdraw energy Q

from the

hot reservoir and produce an equal amount of work, while undergoing a cycle. The thermal ef-

ficiency of such a cycle would have a value of unity (100%). However, this method of operation

would violate the Kelvin–Planck statement and thus is not allowed. It follows that for any sys-

tem executing a power cycle while operating between two reservoirs, only a portion of the heat

transfer Q

can be obtained as work, and the remainder, Q

, must be discharged by heat trans-

fer to the cold reservoir. That is, the thermal efficiency must be less than 100%. In arriving at

this conclusion it was not necessary to (1) identify the nature of the substance contained within

the system, (2) specify the exact series of processes making up the cycle, or (3) indicate whether

the processes are actual processes or somehow idealized. The conclusion that the thermal effi-

ciency must be less than 100% applies to all power cycles whatever their details of operation.

This may be regarded as a corollary of the second law. Other corollaries follow.

CARNOT COROLLARIES. Since no power cycle can have a thermal efficiency of 100%, it

is of interest to investigate the maximum theoretical efficiency. The maximum theoretical

efficiency for systems undergoing power cycles while communicating thermally with two

thermal reservoirs at different temperatures is evaluated in Sec. 5.5 with reference to the

following two corollaries of the second law, called the Carnot corollaries.

 The thermal efficiency of an irreversible power cycle is always less than the thermal

efficiency of a reversible power cycle when each operates between the same two

thermal reservoirs.

 All reversible power cycles operating between the same two thermal reservoirs have the

same thermal efficiency.

A cycle is considered reversible when there are no irreversibilities within the system as it

undergoes the cycle and heat transfers between the system and reservoirs occur reversibly.

The idea underlying the first Carnot corollary is in agreement with expectations stemming

from the discussion of the second law thus far. Namely, the presence of irreversibilities dur-

ing the execution of a cycle is expected to exact a penalty. If two systems operating between

the same reservoirs each receive the same amount of energy Q

and one executes a reversible

cycle while the other executes an irreversible cycle, it is in accord with intuition that the net

work developed by the irreversible cycle will be less, and it will therefore have the smaller

thermal efficiency.

h 

cycle

 1 

METHODOLOGY

UPDATE

The energy transfers

labeled on Fig 5.5 are

positive in the directions

indicated by the arrows.

Carnot corollaries

Hot

reservoir

Cold

reservoir

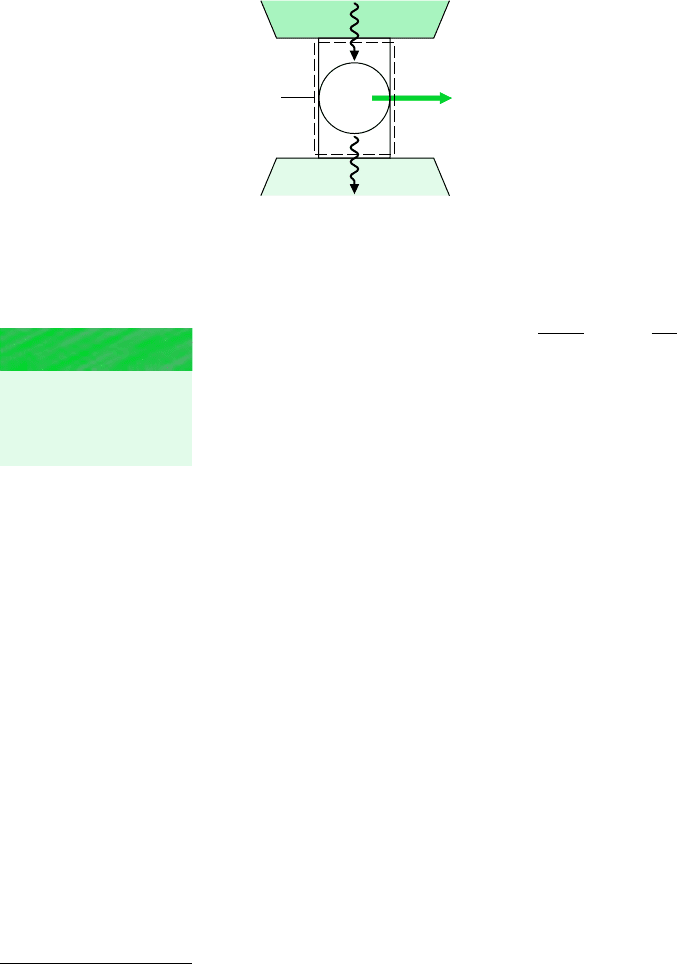
Boundary

cycle

= Q

– Q

 Figure 5.5 System undergoing a power

cycle while exchanging energy by heat transfer

with two reservoirs.

5.3 Applying the Second Law to Thermodynamic Cycles 187

The second Carnot corollary refers only to reversible cycles. All processes of a re-

versible cycle are perfectly executed. Accordingly, if two reversible cycles operating be-

tween the same reservoirs each receive the same amount of energy Q

but one could

produce more work than the other, it could only be as a result of more advantageous se-

lections for the substance making up the system (it is conceivable that, say, air might be

better than water vapor) or the series of processes making up the cycle (nonflow processes

might be preferable to flow processes). This corollary denies both possibilities and indi-

cates that the cycles must have the same efficiency whatever the choices for the working

substance or the series of processes.

The two Carnot corollaries can be demonstrated using the Kelvin–Planck statement of the

second law (see box).

DEMONSTRATING THE CARNOT COROLLARIES

The first Carnot corollary can be demonstrated using the arrangement of Fig. 5.6. A

reversible power cycle R and an irreversible power cycle I operate between the same

two reservoirs and each receives the same amount of energy Q

from the hot reser-

voir. The reversible cycle produces work W

while the irreversible cycle produces

work W

. In accord with the conservation of energy principle, each cycle discharges

energy to the cold reservoir equal to the difference between Q

and the work pro-

duced. Let R now operate in the opposite direction as a refrigeration (or heat pump)

cycle. Since R is reversible, the magnitudes of the energy transfers W

, Q

, and Q

remain the same, but the energy transfers are oppositely directed, as shown by the

dashed lines on Fig. 5.6. Moreover, with R operating in the opposite direction, the hot

reservoir would experience no net change in its condition since it would receive Q

from R while passing Q

to I.

The demonstration of the first Carnot corollary is completed by considering the

combined system shown by the dotted line on Fig. 5.6, which consists of the two cy-

cles and the hot reservoir. Since its parts execute cycles or experience no net change,

the combined system operates in a cycle. Moreover, the combined system exchanges

energy by heat transfer with a single reservoir: the cold reservoir. Accordingly, the com-

bined system must satisfy Eq. 5.1 expressed as

where the inequality is used because the combined system is irreversible in its opera-

tion since irreversible cycle I is one of its parts. Evaluating W

cycle

for the combined

system in terms of the work amounts W

and W

, the above inequality becomes

which shows that W

must be less than W

. Since each cycle receives the same energy

input, Q

, it follows that 

 

and this completes the demonstration.

The second Carnot corollary can be demonstrated in a parallel way by considering

any two reversible cycles R

and R

operating between the same two reservoirs. Then,

letting R

play the role of R and R

the role of I in the previous development, a com-

bined system consisting of the two cycles and the hot reservoir may be formed that

must obey Eq. 5.1. However, in applying Eq. 5.1 to this combined system, the equal-

ity is used because the system is reversible in operation. Thus, it can be concluded that

 W

, and therefore, 

 

. The details are left as an exercise.

 W

6 0

cycle

6 0

1single reservoir2

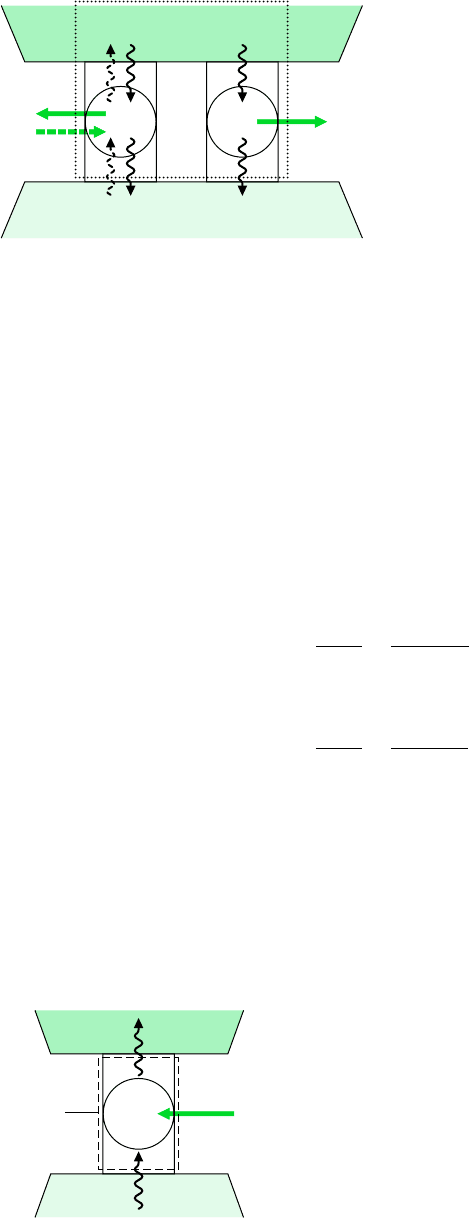
188 Chapter 5 The Second Law of Thermodynamics

Cold reservoir

Q′

= Q

– W

= Q

– W

Dotted line defines combined system

Hot reservoir

 Figure 5.6 Sketch for demonstrating that a

reversible cycle R is more efficient than an

irreversible cycle I when they operate between

the same two reservoirs.

Hot

reservoir

Cold

reservoir

Boundary

cycle

= Q

– Q

+ W

cycle

 Figure 5.7 System undergoing a refrigera-

tion or heat pump cycle while exchanging energy

by heat transfer with two reservoirs.

 5.3.3 Refrigeration and Heat Pump Cycles

Interacting with Two Reservoirs

The second law of thermodynamics places limits on the performance of refrigeration and

heat pump cycles as it does for power cycles. Consider Fig. 5.7, which shows a system

undergoing a cycle while communicating thermally with two thermal reservoirs, a hot and a

cold reservoir. The energy transfers labeled on the figure are in the directions indicated by

the arrows. In accord with the conservation of energy principle, the cycle discharges energy

by heat transfer to the hot reservoir equal to the sum of the energy Q

received by heat

transfer from the cold reservoir and the net work input. This cycle might be a refrigeration

cycle or a heat pump cycle, depending on whether its function is to remove energy Q

from

the cold reservoir or deliver energy Q

to the hot reservoir.

For a refrigeration cycle the coefficient of performance is

(5.3)

The coefficient of performance for a heat pump cycle is

(5.4)

As the net work input to the cycle W

cycle

tends to zero, the coefficients of performance given

by Eqs. 5.3 and 5.4 approach a value of infinity. If W

cycle

were identically zero, the system

of Fig. 5.7 would withdraw energy Q

from the cold reservoir and deliver energy Q

to the

hot reservoir, while undergoing a cycle. However, this method of operation would violate the

Clausius statement of the second law and thus is not allowed. It follows that these coeffi-

cients of performance must invariably be finite in value. This may be regarded as another

corollary of the second law. Further corollaries follow.

g 

cycle



 Q

b 

cycle



 Q

5.3 Applying the Second Law to Thermodynamic Cycles 189

COROLLARIES FOR REFRIGERATION AND HEAT PUMP CYCLES. The maximum

theoretical coefficients of performance for systems undergoing refrigeration and heat pump

cycles while communicating thermally with two reservoirs at different temperatures are

evaluated in Sec. 5.5 with reference to the following corollaries of the second law:

 The coefficient of performance of an irreversible refrigeration cycle is always less than

the coefficient of performance of a reversible refrigeration cycle when each operates

between the same two thermal reservoirs.

 All reversible refrigeration cycles operating between the same two thermal reservoirs

have the same coefficient of performance.

By replacing the term refrigeration with heat pump, we obtain counterpart corollaries for

heat pump cycles.

The first of these corollaries agrees with expectations stemming from the discussion of the

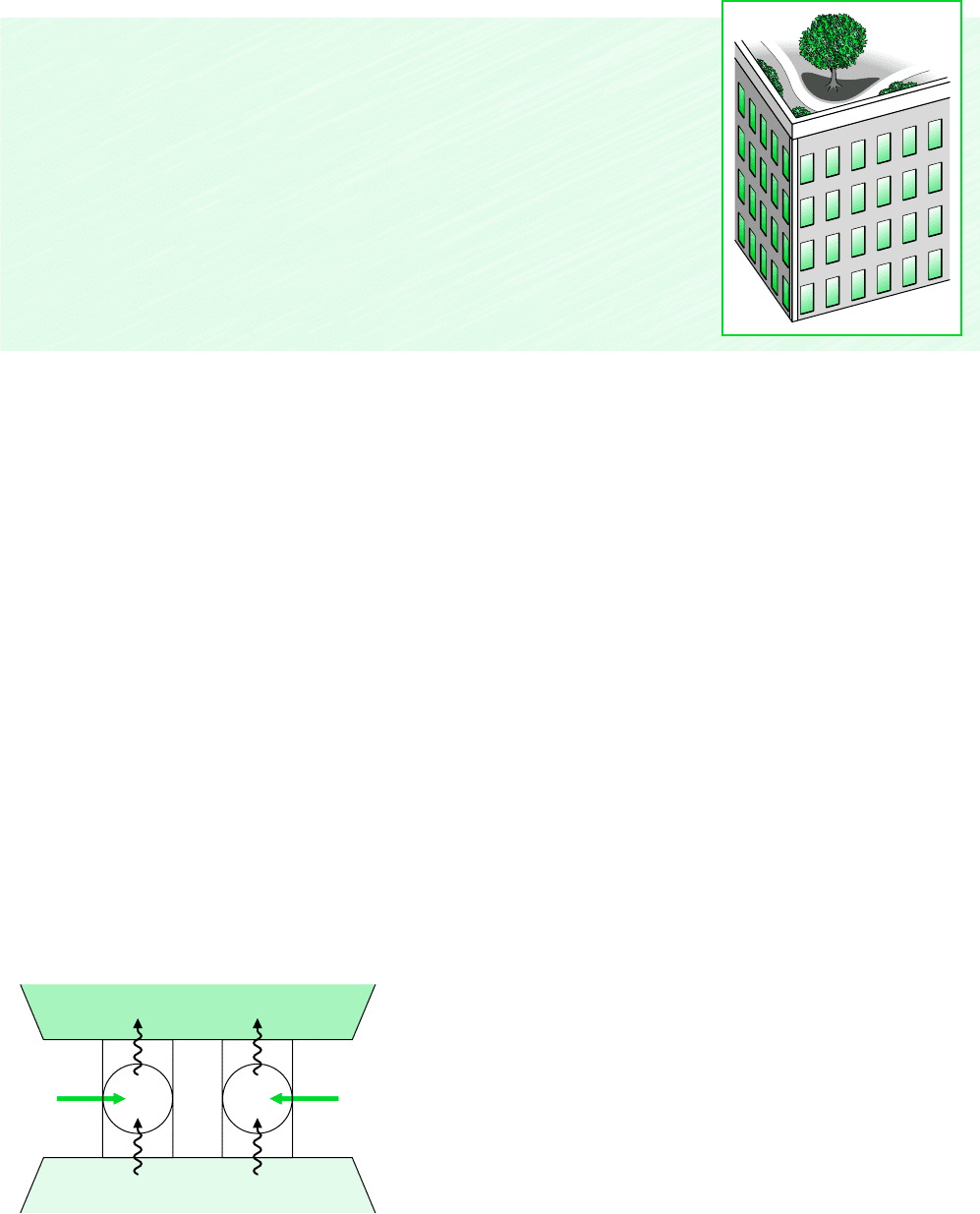
second law thus far. To explore this, consider Fig. 5.8, which shows a reversible refrigeration

cycle R and an irreversible refrigeration cycle I operating between the same two reservoirs.

Each cycle removes the same energy Q

from the cold reservoir. The net work input required

to operate R is W

, while the net work input for I is W

. Each cycle discharges energy by heat

transfer to the hot reservoir equal to the sum of Q

and the net work input. The directions of

the energy transfers are shown by arrows on Fig. 5.8. The presence of irreversibilities during

the operation of a refrigeration cycle is expected to exact a penalty. If two refrigerators working

City planners are com-

bating heat islands. In

Chicago, the once gravel-

roofed City Hall is now

topped by a garden, with

20,000 vines, shrubs, and

trees that absorb solar en-

ergy without increasing the

roof temperature. The roof

temperature in August is as

much as 75F cooler than on

nearby buildings, city

sources report.

Urban Heat Islands Worrisome

Thermodynamics in the News...

Warm blankets of pollution-laden air surround major cities.

Sunlight-absorbing rooftops and expanses of pavement, to-

gether with little greenery, conspire with other features of

city living to raise urban temperatures as much as 10F

above adjacent rural areas. Health-care professionals worry

about the impact of these “heat islands,” especially on the

elderly.

Paradoxically, the hot exhaust from the air conditioners

city dwellers use to keep cool also make sweltering

neighborhoods even hotter. Recent studies indicate that air-

conditioner exhaust accounts for as much as 2F of the urban

temperature rise. Vehicles and commercial activity also

contribute.

Cold reservoir

IRW

Q′

= Q

+ W

= Q

+ W

Hot reservoir

 Figure 5.8 Sketch for demonstrating that a

reversible refrigeration cycle R has a greater co-

efficient of performance than an irreversible cy-

cle I when they operate between the same two

reservoirs.

between the same reservoirs each receive an identical energy transfer from the cold reservoir,

, and one executes a reversible cycle while the other executes an irreversible cycle, we ex-

pect the irreversible cycle to require a greater net work input and thus to have a smaller

coefficient of performance. By a simple extension it follows that all reversible refrigeration

cycles operating between the same two reservoirs have the same coefficient of performance.

Similar arguments apply to the counterpart heat pump cycle statements.

These corollaries can be demonstrated formally using the Kelvin–Planck statement of the

second law and a procedure similar to that employed for the Carnot corollaries. The details

are left as an exercise.

190 Chapter 5 The Second Law of Thermodynamics



5.4 Defining the Kelvin Temperature Scale

The results of Sec. 5.3 establish theoretical upper limits on the performance of power,

refrigeration, and heat pump cycles communicating thermally with two reservoirs. Expres-

sions for the maximum theoretical thermal efficiency of power cycles and the maximum

theoretical coefficients of performance of refrigeration and heat pump cycles are developed

in Sec. 5.5 using the Kelvin temperature scale defined in the present section.

From the second Carnot corollary we know that all reversible power cycles operating

between the same two thermal reservoirs have the same thermal efficiency, regardless of the

nature of the substance making up the system executing the cycle or the series of processes.

Since the efficiency is independent of these factors, its value can be related only to the

nature of the reservoirs themselves. Noting that it is the difference in temperature between

the two reservoirs that provides the impetus for heat transfer between them, and thereby for

the production of work during the cycle, we reason that the efficiency depends only on the

temperatures of the two reservoirs.

From Eq. 5.2 it also follows that for such reversible power cycles the ratio of the heat

transfers Q

Q

depends only on the reservoir temperatures. That is

(5.5)

where 

and 

denote the temperatures of the reservoirs and the function  is for the present

unspecified. Note that the words “rev cycle” are added to this expression to emphasize that

it applies only to systems undergoing reversible cycles while operating between two thermal

reservoirs.

KELVIN SCALE

Equation 5.5 provides a basis for defining a thermodynamic temperature scale: a scale inde-

pendent of the properties of any substance. There are alternative choices for the function 

that lead to this end. The Kelvin scale is obtained by making a particularly simple choice,

namely,   T

T

, where T is the symbol used to denote temperatures on the Kelvin scale.

With this, Eq. 5.5 becomes

(5.6)

Thus, two temperatures on the Kelvin scale are in the same ratio as the values of the heat

transfers absorbed and rejected, respectively, by a system undergoing a reversible cycle while

communicating thermally with reservoirs at these temperatures.

rev

cycle



rev

cycle

 c1u

, u

Kelvin scale

5.4 Defining the Kelvin Temperature Scale 191

If a reversible power cycle were operated in the opposite direction as a refrigeration or

heat pump cycle, the magnitudes of the energy transfers Q

and Q

would remain the same,

but the energy transfers would be oppositely directed. Accordingly, Eq. 5.6 applies to each

type of cycle considered thus far, provided the system undergoing the cycle operates between

two thermal reservoirs and the cycle is reversible.

Equation 5.6 gives only a ratio of temperatures. To complete the definition of the Kelvin scale,

it is necessary to proceed as in Sec. 1.6 by assigning the value 273.16 K to the temperature at

the triple point of water. Then, if a reversible cycle is operated between a reservoir at 273.16 K

and another reservoir at temperature T, the two temperatures are related according to

(5.7)

where Q

and Q are the heat transfers between the cycle and reservoirs at 273.16 K and tem-

perature T, respectively. In the present case, the heat transfer Q plays the role of the ther-

mometric property. However, since the performance of a reversible cycle is independent of

the makeup of the system executing the cycle, the definition of temperature given by Eq. 5.7

depends in no way on the properties of any substance or class of substances.

In Sec. 1.6 we noted that the Kelvin scale has a zero of 0 K, and lower temperatures than

this are not defined. Let us take up these points by considering a reversible power cycle op-

erating between reservoirs at 273.16 K and a lower temperature T. Referring to Eq. 5.7, we

know that the energy rejected from the cycle by heat transfer Q would not be negative, so T

must be nonnegative. Equation 5.7 also shows that the smaller the value of Q, the lower the

value of T, and conversely. Accordingly, as Q approaches zero the temperature T approaches

zero. It can be concluded that a temperature of zero on the Kelvin scale is the lowest con-

ceivable temperature. This temperature is called the absolute zero, and the Kelvin scale is

called an absolute temperature scale.

INTERNATIONAL TEMPERATURE SCALE

When numerical values of the thermodynamic temperature are to be determined, it is not

possible to use reversible cycles, for these exist only in our imaginations. However, temper-

atures evaluated using the constant-volume gas thermometer introduced in Sec. 1.6 are iden-

tical to those of the Kelvin scale in the range of temperatures where the gas thermometer can

be used. Other empirical approaches can be employed for temperatures above and below the

range accessible to gas thermometry. The Kelvin scale provides a continuous definition of

temperature valid over all ranges and provides an essential connection between the several

empirical measures of temperature.

To provide a standard for temperature measurement taking into account both theoretical

and practical considerations, the International Temperature Scale (ITS) was adopted in 1927.

This scale has been refined and extended in several revisions, most recently in 1990. The

International Temperature Scale of 1990 (ITS-90) is defined in such a way that the temper-

ature measured on it conforms with the thermodynamic temperature, the unit of which is the

kelvin, to within the limits of accuracy of measurement obtainable in 1990. The ITS-90 is

based on the assigned values of temperature of a number of reproducible fixed points

(Table 5.1). Interpolation between the fixed-point temperatures is accomplished by formulas

that give the relation between readings of standard instruments and values of the ITS. In the

range from 0.65 to 5.0 K, ITS-90 is defined by equations giving the temperature as functions

of the vapor pressures of particular helium isotopes. The range from 3.0 to 24.5561 K is

based on measurements using a helium constant-volume gas thermometer. In the range from

13.8033 to 1234.93 K, ITS-90 is defined by means of certain platinum resistance ther-

mometers. Above 1234.9 K the temperature is defined using Planck’s equation for blackbody

radiation and measurements of the intensity of visible-spectrum radiation.

T  273.16 a

rev

cycle

192 Chapter 5 The Second Law of Thermodynamics

TABLE 5.1

Defining Fixed Points of the International

Temperature Scale of 1990

T (K) Substance

State

3 to 5 He Vapor pressure point

13.8033 e-H

Triple point

17 e-H

Vapor pressure point

20.3 e-H

Vapor pressure point

24.5561 Ne Triple point

54.3584 O

Triple point

83.8058 Ar Triple point

234.3156 Hg Triple point

273.16 H

O Triple point

302.9146 Ga Melting point

429.7485 In Freezing point

505.078 Sn Freezing point

692.677 Zn Freezing point

933.473 Al Freezing point

1234.93 Ag Freezing point

1337.33 Au Freezing point

1357.77 Cu Freezing point

He denotes

He or

He; e-H

is hydrogen at the equilibrium

concentration of the ortho- and para-molecular forms.

Triple point: temperature at which the solid, liquid, and vapor

phases are in equilibrium. Melting point, freezing point: temperature,

at a pressure of 101.325 kPa, at which the solid and liquid phases are

in equilibrium.

Source: H. Preston-Thomas, “The International Temperature Scale of

1990 (ITS-90),” Metrologia 27, 3–10 (1990).



5.5 Maximum Performance

Measures for Cycles Operating

Between Two Reservoirs

The discussion of Sec. 5.3 continues in this section with the development of expressions for

the maximum thermal efficiency of power cycles and the maximum coefficients of perform-

ance of refrigeration and heat pump cycles in terms of reservoir temperatures evaluated on

the Kelvin scale. These expressions can be used as standards of comparison for actual power,

refrigeration, and heat pump cycles.

 5.5.1 Power Cycles

The use of Eq. 5.6 in Eq. 5.2 results in an expression for the thermal efficiency of a system

undergoing a reversible power cycle while operating between thermal reservoirs at temper-

atures T

and T

. That is

(5.8)

which is known as the Carnot efficiency.

max

 1 

Carnot efficiency



5.5 Maximum Performance Measures for Cycles Operating Between Two Reservoirs 193

Recalling the two Carnot corollaries, it should be evident that the efficiency given by

Eq. 5.8 is the thermal efficiency of all reversible power cycles operating between two reser-

voirs at temperatures T

and T

, and the maximum efficiency any power cycle can have while

operating between the two reservoirs. By inspection, the value of the Carnot efficiency in-

creases as T

increases and/or T

decreases.

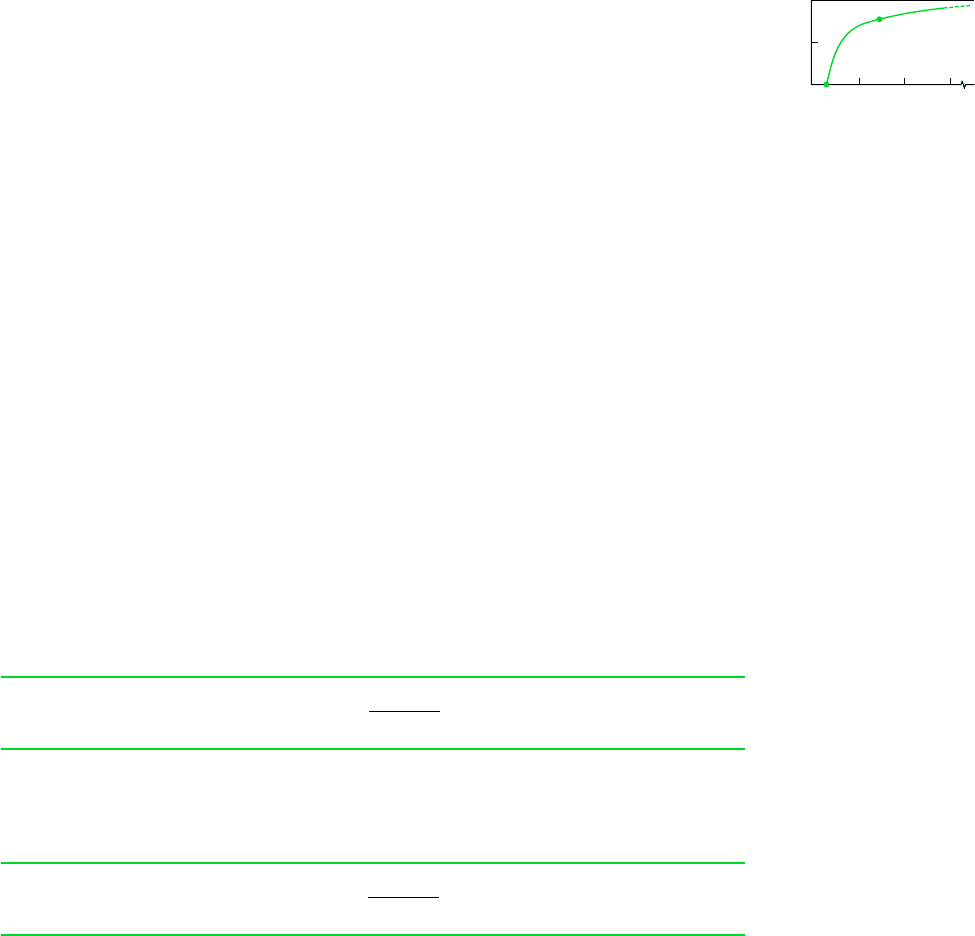
Equation 5.8 is presented graphically in Fig. 5.9. The temperature T

used in constructing

the figure is 298 K in recognition that actual power cycles ultimately discharge energy by heat

transfer at about the temperature of the local atmosphere or cooling water drawn from a nearby

river or lake. Note that the possibility of increasing the thermal efficiency by reducing T

below that of the environment is not practical, for maintaining T

lower than the ambient tem-

perature would require a refrigerator that would have to be supplied work to operate.

Figure 5.9 shows that the thermal efficiency increases with T

. Referring to segment a–b

of the curve, where T

and  are relatively low, we can see that  increases rapidly as T

increases, showing that in this range even a small increase in T

can have a large effect on

efficiency. Though these conclusions, drawn as they are from Fig. 5.9, apply strictly only to

systems undergoing reversible cycles, they are qualitatively correct for actual power cycles.

The thermal efficiencies of actual cycles are observed to increase as the average tempera-

ture at which energy is added by heat transfer increases and/or the average temperature at

which energy is discharged by heat transfer is reduced. However, maximizing the thermal

efficiency of a power cycle may not be the only objective. In practice, other considerations

such as cost may be overriding.

COMMENT. Conventional power-producing cycles have thermal efficiencies ranging up to

about 40%. This value may seem low, but the comparison should be made with an appropri-

ate limiting value and not 100%.  for example. . . consider a system executing a power

cycle for which the average temperature of heat addition is 745 K and the average tempera-

ture at which heat is discharged is 298 K. For a reversible cycle receiving and discharging en-

ergy by heat transfer at these temperatures, the thermal efficiency given by Eq. 5.8 is 60%.

When compared to this value, an actual thermal efficiency of 40% does not appear to be so

low. The cycle would be operating at two-thirds of the theoretical maximum. 

A more complete discussion of power cycles is provided in Chaps. 8 and 9.

 5.5.2 Refrigeration and Heat Pump Cycles

Equation 5.6 is also applicable to reversible refrigeration and heat pump cycles operating

between two thermal reservoirs, but for these Q

represents the heat added to the cycle from

the cold reservoir at temperature T

on the Kelvin scale and Q

is the heat discharged to the

hot reservoir at temperature T

. Introducing Eq. 5.6 in Eq. 5.3 results in the following

expression for the coefficient of performance of any system undergoing a reversible

refrigeration cycle while operating between the two reservoirs

(5.9)

Similarly, substituting Eq. 5.6 into Eq. 5.4 gives the following expression for the coefficient

of performance of any system undergoing a reversible heat pump cycle while operating

between the two reservoirs

(5.10)g

max



 T

max



 T

1000 2000

(K)

3000298

0.5

1.0

max

 Figure 5.9 Carnot

efficiency versus T

, for

 298 K.



The development of Eqs. 5.9 and 5.10 is left as an exercise. Note that the temperatures used

to evaluate 

max

and 

max

must be absolute temperatures on the Kelvin or Rankine scale.

From the discussion of Sec. 5.3.3, it follows that Eqs. 5.9 and 5.10 are the maximum

coefficients of performance that any refrigeration and heat pump cycles can have while operating

between reservoirs at temperatures T

and T

. As for the case of the Carnot efficiency, these

expressions can be used as standards of comparison for actual refrigerators and heat pumps. A

more complete discussion of refrigeration and heat pump cycles is provided in Chap. 10.

 5.5.3 Power Cycle, Refrigeration and Heat Pump Applications

In this section, three examples are provided that illustrate the use of the second law corollaries

of Secs. 5.3.2 and 5.3.3 together with Eqs. 5.8, 5.9, and 5.10, as appropriate.

The first example uses Eq. 5.8 to evaluate an inventor’s claim.

In the next example, we evaluate the coefficient of performance of a refrigerator and com-

pare it with the maximum theoretical value.

194 Chapter 5 The Second Law of Thermodynamics

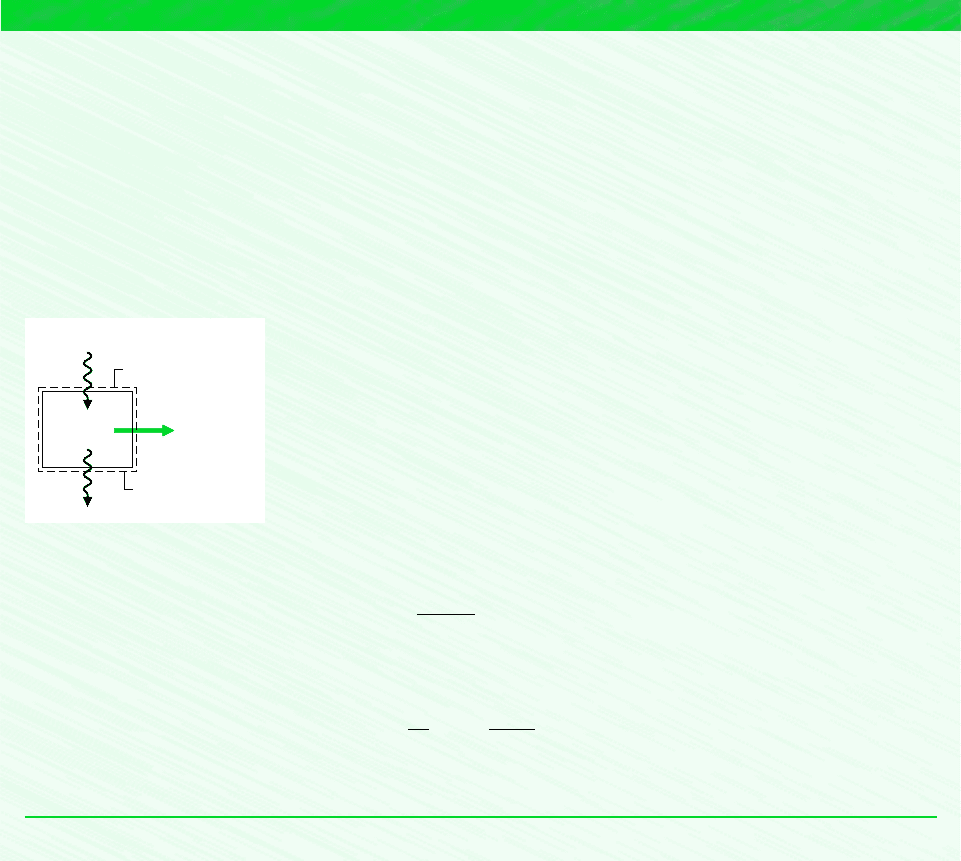
EXAMPLE 5.1 Evaluating a Power Cycle Performance Claim

An inventor claims to have developed a power cycle capable of delivering a net work output of 410 kJ for an energy input by

heat transfer of 1000 kJ. The system undergoing the cycle receives the heat transfer from hot gases at a temperature of 500 K

and discharges energy by heat transfer to the atmosphere at 300 K. Evaluate this claim.

SOLUTION

Known: A system operates in a cycle and produces a net amount of work while receiving and discharging energy by heat

transfer at fixed temperatures.

Find: Evaluate the claim that the cycle can develop 410 kJ of work for an energy input by heat of 1000 kJ.

Schematic and Given Data:

Analysis: Inserting the values supplied by the inventor into Eq. 5.2, the cycle thermal efficiency is

The maximum thermal efficiency any power cycle can have while operating between reservoirs at T

 500 K and T



300 K is given by Eq. 5.8.

Since the thermal efficiency of the actual cycle exceeds the maximum theoretical value, the claim cannot be valid.

The temperatures used in evaluating 

max

must be in K or R.

max

 1 

300 K

500 K

 0.40 140%2

h 

410 kJ

1000 kJ

 0.41 141%2

❶

Power

cycle

= 1000 kJ

out

W = 410 kJ

500 K

300 K

Assumptions:

1. The system is shown on the accompanying figure.

2. The hot gases and the atmosphere play the roles of hot and cold reservoirs, respectively.

 Figure E5.1

5.5 Maximum Performance Measures for Cycles Operating Between Two Reservoirs 195

In Example 5.3, we determine the minimum theoretical work input and cost for one day

of operation of an electric heat pump.

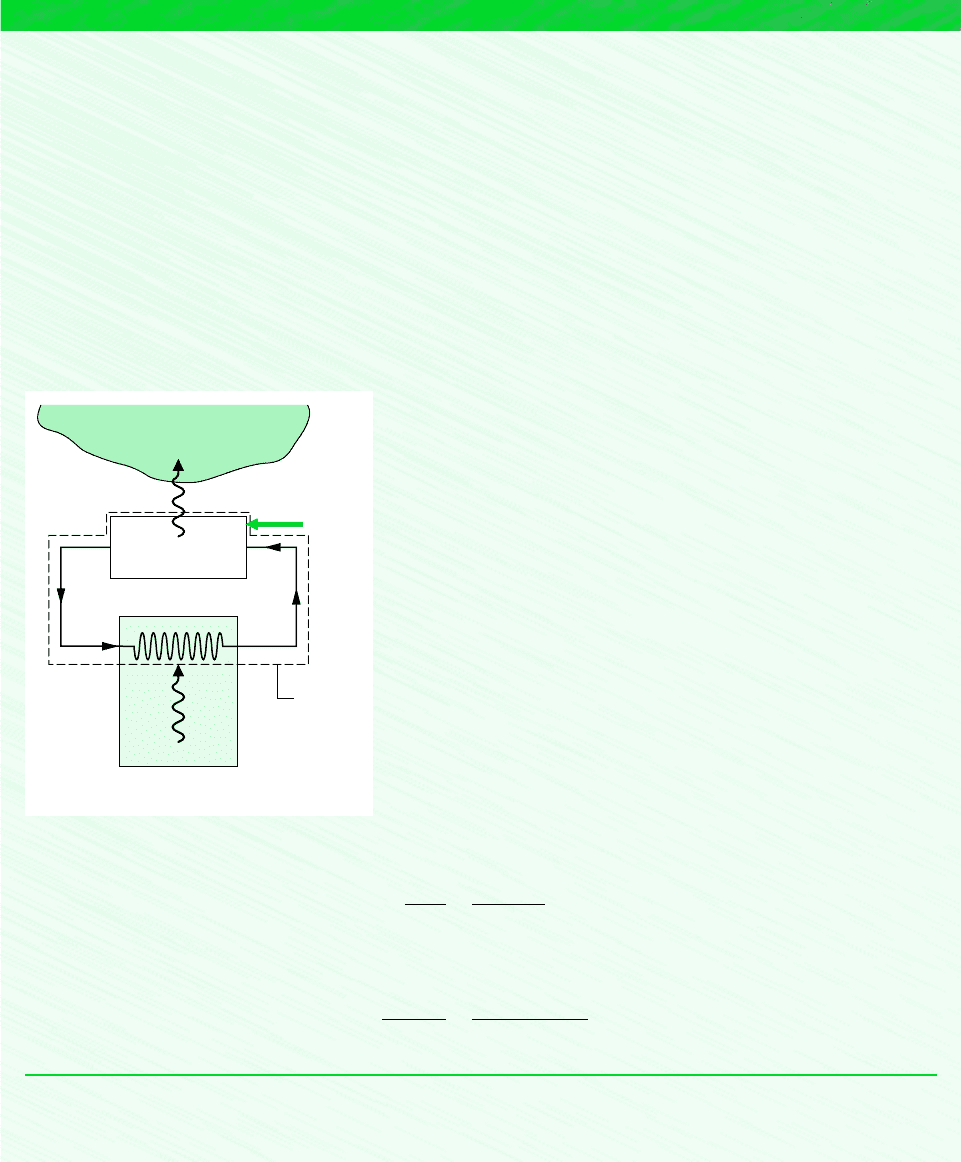
EXAMPLE 5.2 Evaluating Refrigerator Performance

By steadily circulating a refrigerant at low temperature through passages in the walls of the freezer compartment, a refrigerator

maintains the freezer compartment at 5C when the air surrounding the refrigerator is at 22C. The rate of heat transfer from

the freezer compartment to the refrigerant is 8000 kJ/h and the power input required to operate the refrigerator is 3200 kJ/h.

Determine the coefficient of performance of the refrigerator and compare with the coefficient of performance of a reversible

refrigeration cycle operating between reservoirs at the same two temperatures.

SOLUTION

Known: A refrigerator maintains a freezer compartment at a specified temperature. The rate of heat transfer from the

refrigerated space, the power input to operate the refrigerator, and the ambient temperature are known.

Find: Determine the coefficient of performance and compare with that of a reversible refrigerator operating between reser-

voirs at the same two temperatures.

Schematic and Given Data:

Analysis: Inserting the given operating data into Eq. 5.3, the coefficient of performance of the refrigerator is

Substituting values into Eq. 5.9 gives the coefficient of performance of a reversible refrigeration cycle operating between

reservoirs at T

 268 K and T

 295 K

The difference between the actual and maximum coefficients of performance suggests that there may be some potential

for improving the thermodynamic performance. This objective should be approached judiciously, however, for improved

performance may require increases in size, complexity, and cost.

max



 T



268 K

295 K  268 K

 9.9

b 

cycle



8000 kJ/h

3200 kJ/h

 2.5

❶

Freezer compartment

at –5°C (268 K)

System

boundary

Surroundings at 22°C (295 K)

= 8000 kJ/h

cycle

= 3200 kJ/h

Assumptions:

1. The system shown on the accompanying figure is at steady state.

2. The freezer compartment and the surrounding air play the roles of cold

and hot reservoirs, respectively.

 Figure E5.2

❶