Moran M.J., Shapiro H.N. Fundamentals of Engineering Thermodynamics

Подождите немного. Документ загружается.

226 Chapter 6 Using Entropy

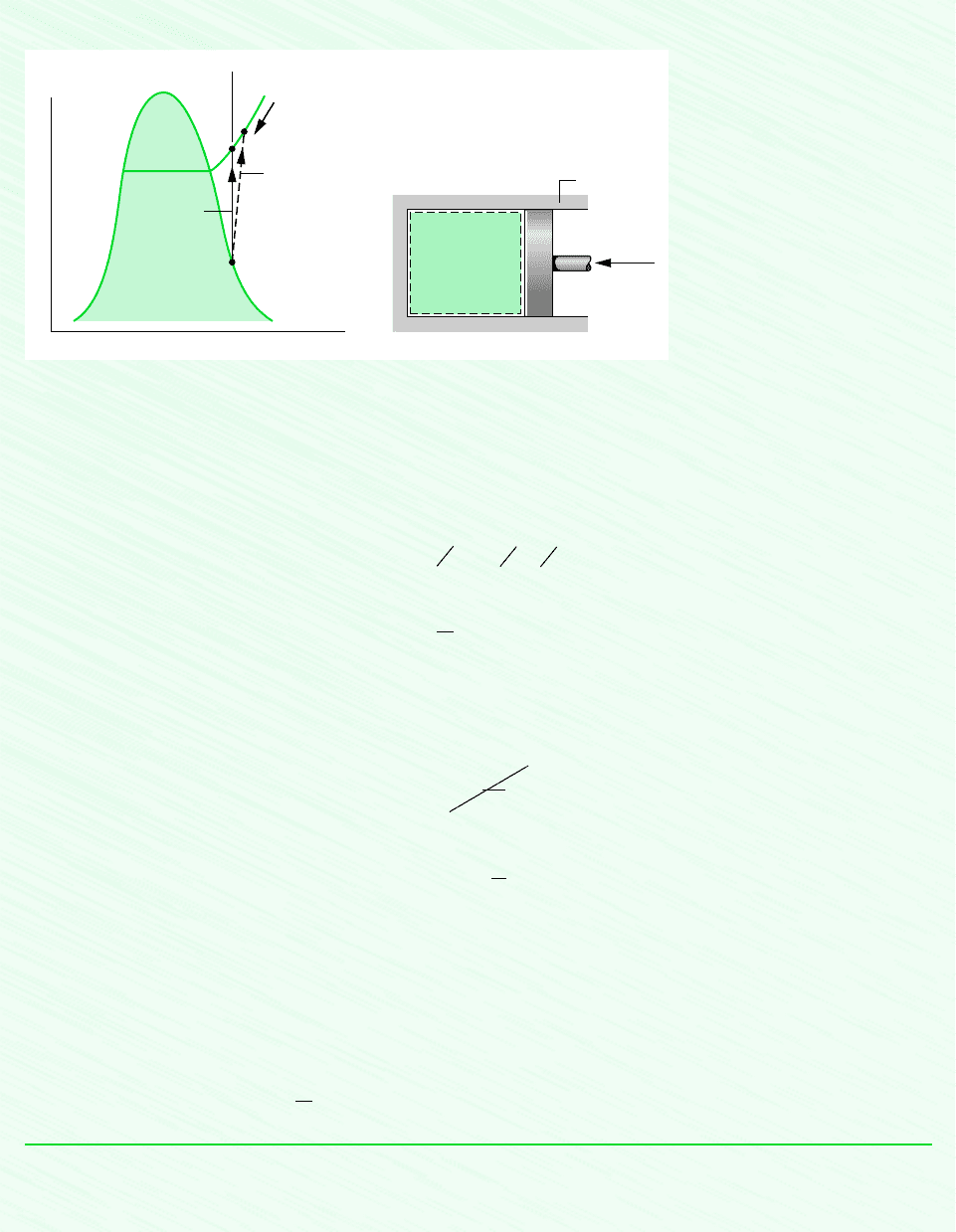
❶

Internally

reversible

compression

Actual

compression

Internal

energy

decreases

Accessible

states

R-134a

Insulation

 Figure E6.3

Schematic and Given Data:

Assumptions:

1. The Refrigerant 134a is a closed system.

2. There is no heat transfer with the surroundings.

3. The initial and final states are equilibrium states. There is no change in kinetic or potential energy between these states.

Analysis: An expression for the work can be obtained from an energy balance. By applying assumptions 2 and 3

When written on a unit mass basis, the work input is then

The specific internal energy u

can be obtained from Table A-10 as u

 227.06 kJ/kg. Since u

is known, the value for the

work input depends on the specific internal energy u

. The minimum work input corresponds to the smallest allowed value

for u

, determined using the second law as follows.

Applying an entropy balance

where the entropy transfer term is set equal to zero because the process is adiabatic. Thus, the allowed final states must satisfy

The restriction indicated by the foregoing equation can be interpreted using the accompanying T–s diagram. Since  cannot

be negative, states with s

 s

are not accessible adiabatically. When irreversibilities are present during the compression, en-

tropy is produced, so s

 s

. The state labeled 2s on the diagram would be attained in the limit as irreversibilities are reduced

to zero. This state corresponds to an isentropic compression.

By inspection of Table A-12, we see that when pressure is fixed, the specific internal energy decreases as temperature

decreases. Thus, the smallest allowed value for u

corresponds to state 2s. Interpolating in Table A-12 at 0.7 MPa, with

 s

 0.9190 kJ/kg  K, we find that u

 244.32 kJ/kg. Finally, the minimum work input is

The effect of irreversibilities exacts a penalty on the work input required: A greater work input is needed for the actual

adiabatic compression process than for an internally reversible adiabatic process between the same initial state and the

same final pressure.

a

min

 u

 u

 244.32  227.06  17.26 kJ/kg

 s



 0

¢S 



 s

a

b u

 u

¢U  ¢KE

 ¢PE

 Q

 W

❶

6.5 Entropy Balance for Closed Systems 227

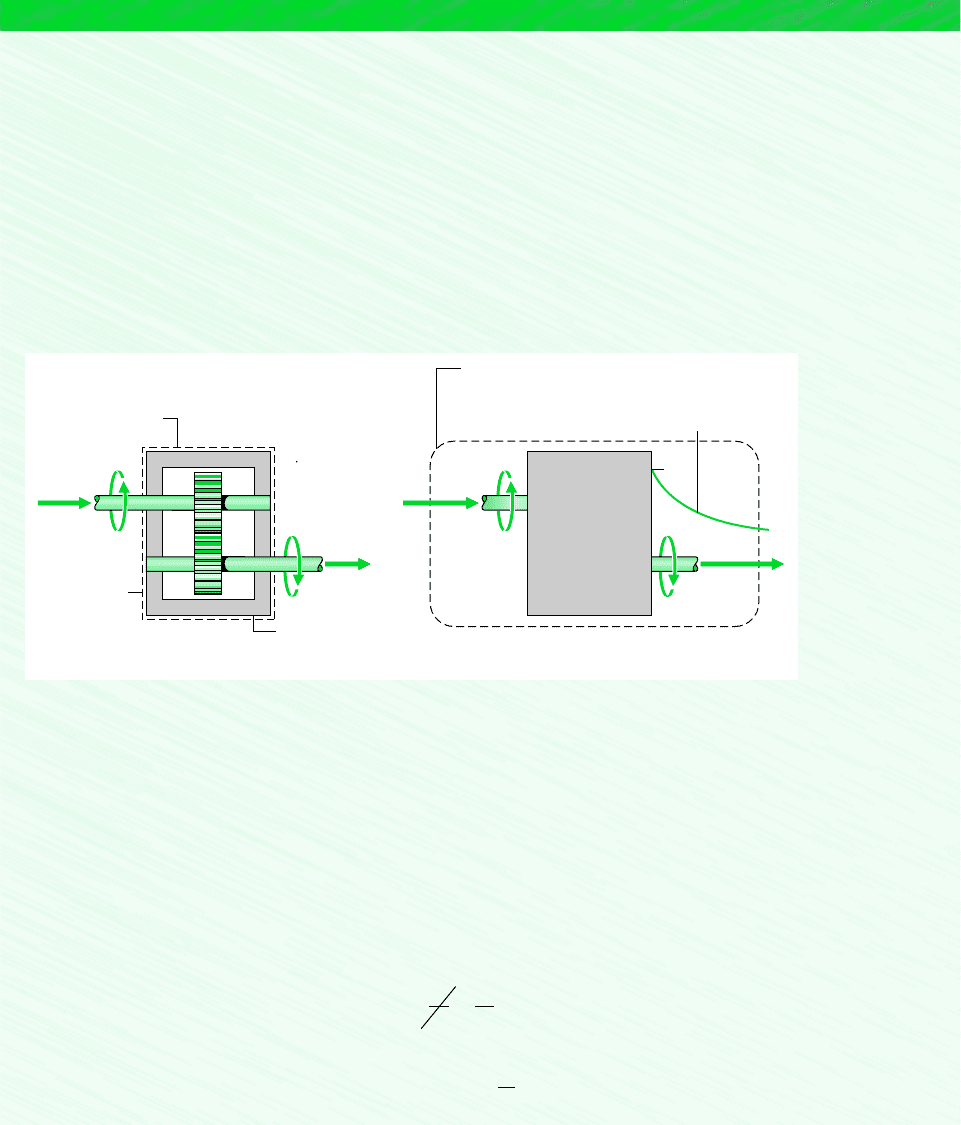
EXAMPLE 6.4 Pinpointing Irreversibilities

Referring to Example 2.4, evaluate the rate of entropy production in kW/K, for (a) the gearbox as the system and (b) an

enlarged system consisting of the gearbox and enough of its surroundings that heat transfer occurs at the temperature of the

surroundings away from the immediate vicinity of the gearbox, T

 293 K (20C).

SOLUTION

Known: A gearbox operates at steady state with known values for the power input through the high-speed shaft, power out-

put through the low-speed shaft, and heat transfer rate. The temperature on the outer surface of the gearbox and the temper-

ature of the surroundings away from the gearbox are also known.

Find: Evaluate the entropy production rate for each of the two specified systems shown in the schematic.

Schematic and Given Data:

To pinpoint the relative significance of the internal and external irreversibilities, the next

example illustrates the application of the entropy rate balance to a system and to an enlarged

system consisting of the system and a portion of its immediate surroundings.

System

boundary

Q = –1.2 kW

58.8 kW

60 kW

Gearbox

= 300 K

58.8 kW

60 kW

At this

boundary the

temperature is

= 293 K

Temperature

variation

(a)(b)

 Figure E6.4

Assumptions:

1. In part (a), the gearbox is taken as a closed system operating at steady state, as shown on the accompanying sketch labeled

with data from Example 2.4.

2. In part (b) the gearbox and a portion of its surroundings are taken as a closed system, as shown on the accompanying

sketch labeled with data from Example 2.4.

3. The temperature of the outer surface of the gearbox and the temperature of the surroundings are each uniform.

Analysis:

(a) To obtain an expression for the entropy production rate, begin with the entropy balance for a closed system on a time rate

basis: Eq. 6.32. Since heat transfer takes place only at temperature T

, the entropy rate balance reduces at steady state to

Solving





 s

 6.5.5 Increase of Entropy Principle

Our study of the second law began in Sec. 5.1 with a discussion of the directionality of

processes. In the present development, it is shown that the energy and entropy balances can

be used together to determine direction.

The present discussion centers on an enlarged system comprising a system and that por-

tion of the surroundings affected by the system as it undergoes a process. Since all energy

and mass transfers taking place are included within the boundary of the enlarged system, the

enlarged system can be regarded as an isolated system.

An energy balance for the isolated system reduces to

(6.34a)

because no energy transfers take place across its boundary. Thus, the energy of the isolated

system remains constant. Since energy is an extensive property, its value for the isolated sys-

tem is the sum of its values for the system and surroundings, respectively, so Eq. 6.34a can

be written as

(6.34b)

In either of these forms, the conservation of energy principle places a constraint on the processes

that can occur. For a process to take place, it is necessary for the energy of the system plus the

surroundings to remain constant. However, not all processes for which this constraint is satis-

fied can actually occur. Processes also must satisfy the second law, as discussed next.

An entropy balance for the isolated system reduces to

(6.35a)

¢S 4

isol

 s

isol

¢S 4

isol





 s

isol

¢E 4

system

 ¢E 4

surr

 0

¢E 4

isol

 0

228 Chapter 6 Using Entropy

Introducing the known values for the heat transfer rate and the surface temperature T

(b) Since heat transfer takes place at temperature T

for the enlarged system, the entropy rate balance reduces at steady state to

Solving

Introducing the known values for the heat transfer rate and the temperature T

The value of the entropy production rate calculated in part (a) gauges the significance of irreversibilities associated with fric-

tion and heat transfer within the gearbox. In part (b), an additional source of irreversibility is included in the enlarged system,

namely the irreversibility associated with the heat transfer from the outer surface of the gearbox at T

to the surroundings at T

In this case, the irreversibilities within the gearbox are dominant, accounting for 97.6% of the total rate of entropy production.



11.2 kW2

1293 K2

 4.1  10

3

kW/K





 s



11.2 kW2

1300 K2

 4  10

3

kW/K

❶

6.5 Entropy Balance for Closed Systems 229

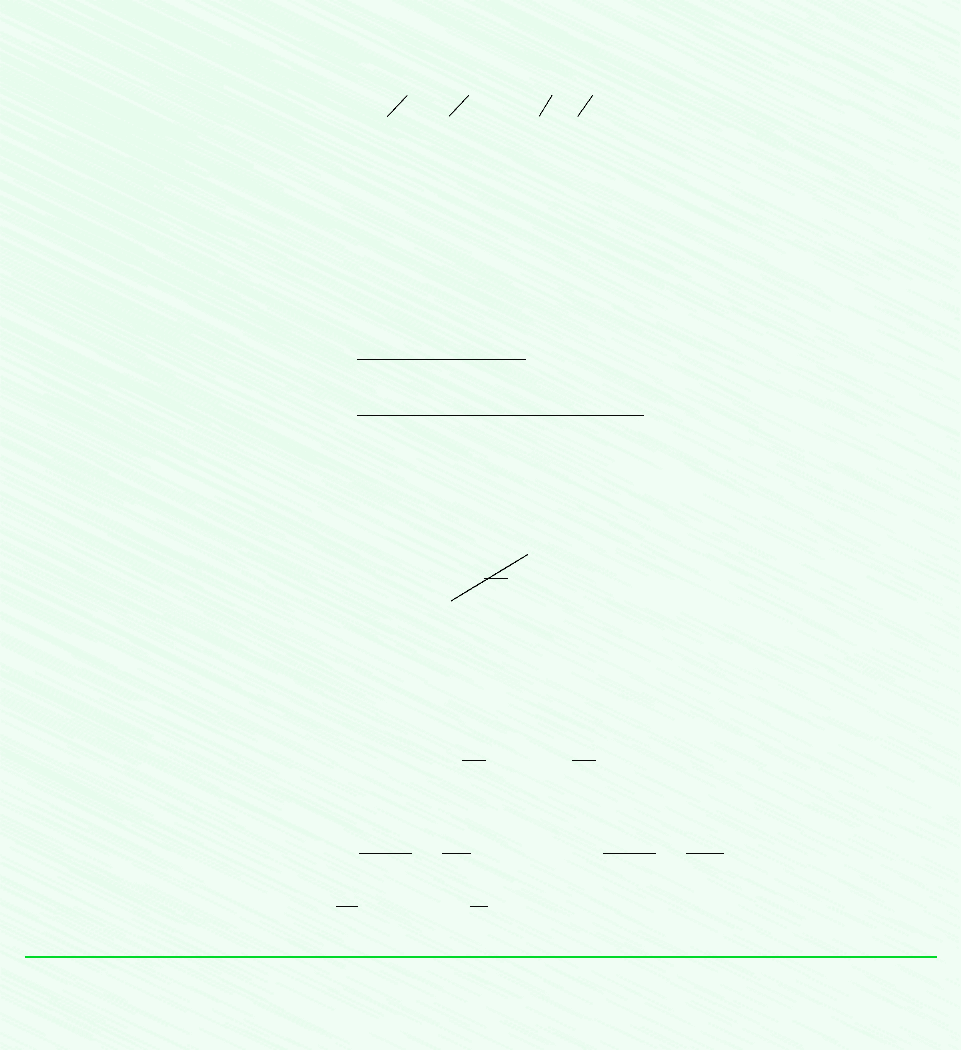
EXAMPLE 6.5 Quenching a Hot Metal Bar

A 0.3 kg metal bar initially at 1200K is removed from an oven and quenched by immersing it in a closed tank containing

9 kg of water initially at 300K. Each substance can be modeled as incompressible. An appropriate constant specific heat value

for the water is c

 4.2 kJ/kg  K, and an appropriate value for the metal is c

 0.42 kJ/kg  K. Heat transfer from the tank

contents can be neglected. Determine (a) the final equilibrium temperature of the metal bar and the water, in K, and (b) the

amount of entropy produced, in kJ/.

SOLUTION

Known: A hot metal bar is quenched by immersing it in a tank containing water.

Find: Determine the final equilibrium temperature of the metal bar and the water, and the amount of entropy produced.

Schematic and Given Data:

System boundary

Water:

= 300°K

= 4.2 kJ/kg · Κ

Metal bar:

= 1200°Κ

= 0.42 kJ/kg · Κ

= 0.3 kg

= 9 kg

Assumptions:

1. The metal bar and the water within the tank form a closed system,

as shown on the accompanying sketch.

2. There is no energy transfer by heat or work: The system is isolated.

3. There is no change in kinetic or potential energy.

4. The water and metal bar are each modeled as incompressible with

known specific heats.

 Figure E6.5

where 

isol

is the total amount of entropy produced within the system and its surroundings.

Since entropy is produced in all actual processes, the only processes that can occur are those

for which the entropy of the isolated system increases. This is known as the increase of

entropy principle. The increase of entropy principle is sometimes considered an alternative

statement of the second law.

Since entropy is an extensive property, its value for the isolated system is the sum of its

values for the system and surroundings, respectively, so Eq. 6.35a can be written as

(6.35b)

Notice that this equation does not require the entropy change to be positive for both the

system and surroundings but only that the sum of the changes is positive. In either of

these forms, the increase of entropy principle dictates the direction in which any process

can proceed: the direction that causes the total entropy of the system plus surroundings

to increase.

We noted previously the tendency of systems left to themselves to undergo processes

until a condition of equilibrium is attained (Sec. 5.1). The increase of entropy principle

suggests that the entropy of an isolated system increases as the state of equilibrium is

approached, with the equilibrium state being attained when the entropy reaches a maxi-

mum. This interpretation is considered again in Sec. 14.1, which deals with equilibrium

criteria.

The example to follow illustrates the increase of entropy principle.

¢S 4

system

 ¢S 4

surr

 s

isol

increase of entropy

principle

230 Chapter 6 Using Entropy

Analysis:

(a) The final equilibrium temperature can be evaluated from an energy balance

where the indicated terms vanish by assumptions 2 and 3. Since internal energy is an extensive property, its value for the over-

all system is the sum of the values for the water and metal, respectively. Thus, the energy balance becomes

Using Eq. 3.20a to evaluate the internal energy changes of the water and metal in terms of the constant specific heats

where T

is the final equilibrium temperature, and T

and T

are the initial temperatures of the water and metal, respectively. Solv-

ing for T

and inserting values

(b) The amount of entropy production can be evaluated from an entropy balance. Since no heat transfer occurs between the

system and its surroundings, there is no accompanying entropy transfer, and an entropy balance for the system reduces to

Entropy is an extensive property, so its value for the system is the sum of its values for the water and the metal, respectively,

and the entropy balance becomes

Evaluating the entropy changes using Eq. 6.24 for incompressible substances, the foregoing equation can be written as

Inserting values

The metal bar experiences a decrease in entropy. The entropy of the water increases. In accord with the increase of en-

tropy principle, the entropy of the isolated system increases.

The value of  is sensitive to roundoff in the value of T

 a0.3761

°K

b a0.1734

b 0.2027 kJ/°K

s  19 kg2 a4.2

°K

b ln

303

300

 10.3 kg2 a0.42

°K

b ln

303

1200

s  m

 m

¢S

water

 ¢S

metal

 s

¢S 



 s

 303°K



19 kg211021300°K2 10.3 kg211200°K2

19 kg21102 10.3 kg2





 m



2 m

 T

2 m

 T

2 0

¢U

water

 ¢U

metal

 0

¢KE

 ¢PE

 ¢U  Q

 W

❷

❶

STATISTICAL INTERPRETATION OF ENTROPY

In statistical thermodynamics, entropy is associated with the notion of disorder and the sec-

ond law statement that the entropy of an isolated system undergoing a spontaneous process

tends to increase is equivalent to saying that the disorder of the isolated system tends to in-

crease. Let us conclude the present discussion with a brief summary of concepts from the

microscopic viewpoint related to these ideas.

❶

❷

6.6 Entropy Rate Balance for Control Volumes 231



6.6 Entropy Rate Balance for

Control Volumes

Thus far the discussion of the entropy balance concept has been restricted to the case of

closed systems. In the present section the entropy balance is extended to control volumes.

Like mass and energy, entropy is an extensive property, so it too can be transferred into

or out of a control volume by streams of matter. Since this is the principal difference be-

tween the closed system and control volume forms, the control volume entropy rate balance

can be obtained by modifying Eq. 6.32 to account for these entropy transfers. The result

(6.37)

rate of rates of rate of

entropy entropy entropy

change transfer production







 s

no new fundamental

understanding.

The new statistical

definition reduces to

the Boltzmann rela-

tion for systems at

equilibrium. But for

systems at states far

from equilibrium the

new definition shines, say its supporters. The theory uses the

mathematical notion of fractals to account for nonequilibrium

behavior and describes systems on the verge of chaos by new

statistical descriptions. Time will tell whether the new defini-

tion is accepted as the basis of statistical mechanics, or takes

its place on a long list of bright ideas that fell by the wayside

of science.

Roll Over Boltzmann

Thermodynamics in the News…

Physicist Constantino Tsallis has proposed a new statistical

definition of entropy some say will shake the foundations of

science as we know it. The Boltzmann relation, providing the

link between the microscopic interpretation of entropy and ob-

servations of macroscopic system behavior for over a century,

is being called into question. Scientists are weighing in on

whether the theory provides new fundamental understanding

or simply amplifies our thinking.

Supporters of the new definition of entropy say it extends

the scope of statistical thermodynamics to new and exciting

classes of problems. They claim it fills a gap in theory first

noted by Einstein and allows researchers to explain phenom-

ena ranging from the movement of microorganisms to the mo-

tions of stars, and even swings in the stock market. Skeptics

believe that it only provides an empirical “fudge” factor with

Viewed macroscopically, an equilibrium state of a system appears to be unchanging, but

on the microscopic level the particles making up the matter are continually in motion. Ac-

cordingly, a vast number of possible microscopic states correspond to any given macroscopic

equilibrium state. The total number of possible microscopic states available to a system is

called the thermodynamic probability, w. Entropy is related to w by the Boltzmann relation

w (6.36)

where k is Boltzmann’s constant. From this equation we see that any process that increases

the number of possible microscopic states of a system increases its entropy, and conversely.

Hence, for an isolated system, processes only occur in such a way that the number of mi-

croscopic states available to the system increases. The number w is referred to as the diso-

rder of the system. We can say, then, that the only processes an isolated system can undergo

are those that increase the disorder of the system.

S  k ln

R I P

S = k ln w



control volume entropy

rate balance

232 Chapter 6 Using Entropy

where dS

dt represents the time rate of change of entropy within the control volume.

The terms and account, respectively, for rates of entropy transfer accompany-

ing mass flow into and out of the control volume. The term represents the time rate

of heat transfer at the location on the boundary where the instantaneous temperature is

. The ratio accounts for the accompanying rate of entropy transfer. The term

denotes the time rate of entropy production due to irreversibilities within the control

volume.

INTEGRAL FORM

As for the cases of the control volume mass and energy rate balances, the entropy rate bal-

ance can be expressed in terms of local properties to obtain forms that are more generally

applicable. Thus, the term S

(t), representing the total entropy associated with the control

volume at time t, can be written as a volume integral

where  and s denote, respectively, the local density and specific entropy. The rate of entropy

transfer accompanying heat transfer can be expressed more generally as an integral over the

surface of the control volume

where is the heat flux, the time rate of heat transfer per unit of surface area, through the

location on the boundary where the instantaneous temperature is T. The subscript “b” is added

as a reminder that the integrand is evaluated on the boundary of the control volume. In ad-

dition, the terms accounting for entropy transfer accompanying mass flow can be expressed

as integrals over the inlet and exit flow areas, resulting in the following form of the entropy

rate balance

(6.38)

where V

denotes the normal component in the direction of flow of the velocity relative to

the flow area. In some cases, it is also convenient to express the entropy production rate as

a volume integral of the local volumetric rate of entropy production within the control vol-

ume. The study of Eq. 6.38 brings out the assumptions underlying Eq. 6.37. Finally, note

that for a closed system the sums accounting for entropy transfer at inlets and exits drop

out, and Eq. 6.38 reduces to give a more general form of Eq. 6.32.

 6.6.1 Analyzing Control Volumes at Steady State

Since a great many engineering analyses involve control volumes at steady state, it is in-

structive to list steady-state forms of the balances developed for mass, energy, and entropy.

At steady state, the conservation of mass principle takes the form

(4.27)





rs dV 



dA 



srV

dAb





srV

dAb

 s

time rate of entropy

£transfer accompanying

heat transfer

§



1t2



rs dV



entropy transfer

accompanying mass flow

6.6 Entropy Rate Balance for Control Volumes 233

The energy rate balance at steady state is

(4.28a)

Finally, the steady-state form of the entropy rate balance is obtained by reducing Eq. 6.37

to give

(6.39)

These equations often must be solved simultaneously, together with appropriate property

relations.

Mass and energy are conserved quantities, but entropy is not conserved. Equation 4.27 in-

dicates that at steady state the total rate of mass flow into the control volume equals the total

rate of mass flow out of the control volume. Similarly, Eq. 4.28a indicates that the total rate

of energy transfer into the control volume equals the total rate of energy transfer out of the

control volume. However, Eq. 6.39 requires that the rate at which entropy is transferred out

must exceed the rate at which entropy enters, the difference being the rate of entropy pro-

duction within the control volume owing to irreversibilities.

ONE-INLET, ONE-EXIT CONTROL VOLUMES

Since many applications involve one-inlet, one-exit control volumes at steady state, let us

also list the form of the entropy rate balance for this important case:

Or, on dividing by the mass flow rate and rearranging

(6.40)

The two terms on the right side of Eq. 6.40 denote, respectively, the rate of entropy trans-

fer accompanying heat transfer and the rate of entropy production within the control vol-

ume, each per unit of mass flowing through the control volume. From Eq. 6.40 it can be

concluded that the entropy of a unit of mass passing from inlet to exit can increase, de-

crease, or remain the same. Furthermore, because the value of the second term on the

right can never be negative, a decrease in the specific entropy from inlet to exit can be

realized only when more entropy is transferred out of the control volume accompanying

heat transfer than is produced by irreversibilities within the control volume. When the

value of this entropy transfer term is positive, the specific entropy at the exit is greater

than the specific entropy at the inlet whether internal irreversibilities are present or not.

In the special case where there is no entropy transfer accompanying heat transfer, Eq. 6.40

reduces to

(6.41)

 s



 s



b

0 

 m

 s

2 s

0 





 s

0  Q

 W



 gz

b



 gz

steady-state entropy

rate balance



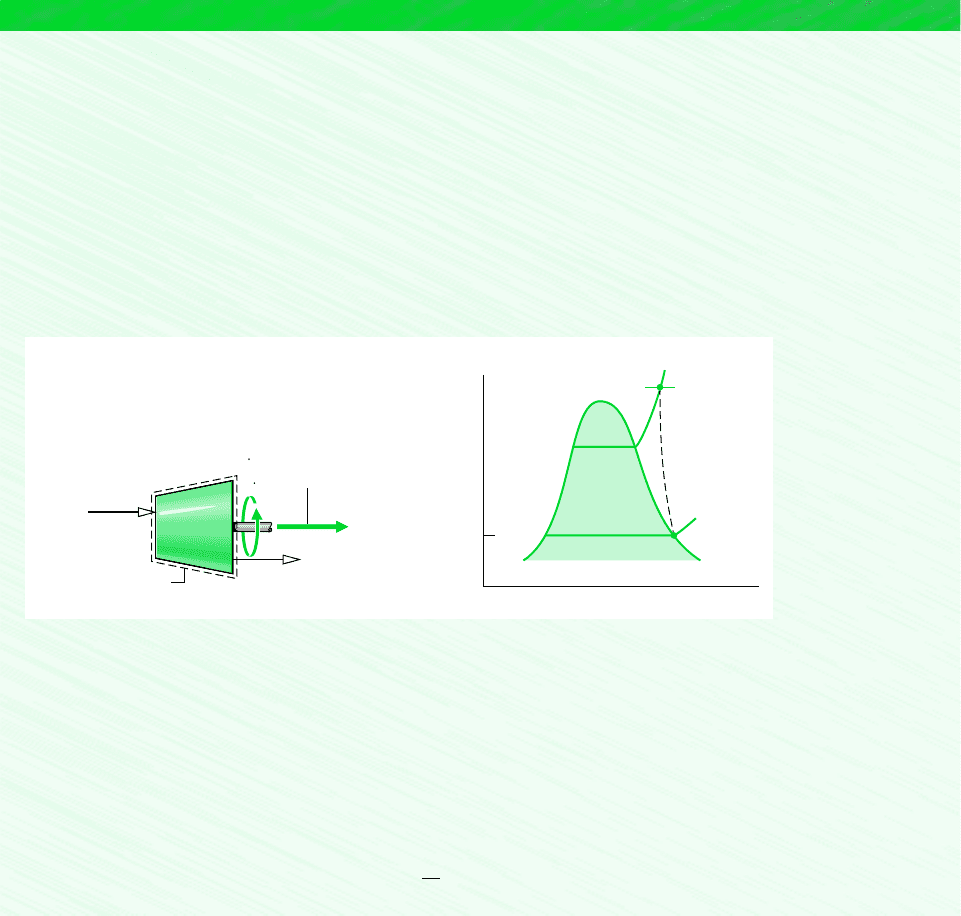
EXAMPLE 6.6 Entropy Production in a Steam Turbine

Steam enters a turbine with a pressure of 30 bar, a temperature of 400C, and a velocity of 160 m/s. Saturated vapor at 100C

exits with a velocity of 100 m /s. At steady state, the turbine develops work equal to 540 kJ per kg of steam flowing through

the turbine. Heat transfer between the turbine and its surroundings occurs at an average outer surface temperature of 350 K.

Determine the rate at which entropy is produced within the turbine per kg of steam flowing, in Neglect the change

in potential energy between inlet and exit.

SOLUTION

Known: Steam expands through a turbine at steady state for which data are provided.

Find: Determine the rate of entropy production per kg of steam flowing.

Schematic and Given Data:

kJ/kg

234 Chapter 6 Using Entropy

Accordingly, when irreversibilities are present within the control volume, the entropy of a

unit of mass increases as it passes from inlet to exit. In the limiting case in which no irre-

versibilities are present, the unit mass passes through the control volume with no change in

its entropy—that is, isentropically.

 6.6.2 Illustrations

The following examples illustrate the use of the mass, energy, and entropy balances for the

analysis of control volumes at steady state. Carefully note that property relations and prop-

erty diagrams also play important roles in arriving at solutions.

In the first example, we evaluate the rate of entropy production within a turbine operat-

ing at steady state when there is heat transfer from the turbine.

Assumptions:

1. The control volume shown on the accompanying sketch is at steady state.

2. Heat transfer from the turbine to the surroundings occurs at a specified average outer surface temperature.

3. The change in potential energy between inlet and exit can be neglected.

Analysis: To determine the entropy production per unit mass flowing through the turbine, begin with mass and entropy rate

balances for the one-inlet, one-exit control volume at steady state:

0 

 m

 m

 s

0  m

 m

 Figure E6.6

= 30 bar

= 400°C

= 160 m/s

= 100°C

Saturated vapor

= 100 m/s

–––

= 540 kJ/kg

= 350 K

400°C

30 bar

100°C

Since heat transfer occurs only at T

 350 K, the first term on the right side of the entropy rate balance reduces to .

Combining the mass and entropy rate balances

where is the mass flow rate. Solving for

The heat transfer rate, , required by this expression is evaluated next.

Reduction of the mass and energy rate balances results in

where the potential energy change from inlet to exit is dropped by assumption 3. From Table A-4 at 30 bar, 400C, h



3230.9 kJ/kg, and from Table A-2, h

 h

(100C)  2676.1 kJ/kg. Thus

From Table A-2, s

 and from Table A-4, s

 Inserting values into the expression

for entropy production

If the boundary were located to include a portion of the immediate surroundings so heat transfer would take place at the

temperature of the surroundings, say T

 293 K, the entropy production for the enlarged control volume would be

It is left as an exercise to verify this value and to explain why the entropy production for the enlarged

control volume would be greater than for a control volume consisting of the turbine only.

0.511 kJ/kg

 0.0646  0.4337  0.4983

kJ/kg



122.6 kJ/ kg2

350 K

 17.3549  6.92122

6.9212 kJ/kg

K.7.3549 kJ/kg

 540  554.8  7.8 22.6 kJ/kg

 540

 12676.1  3230.92 a

b c

11002

 11602

d a

b `

1 kg

m/s

` `



 1h

 h

2 a

 V







 1s

 s



0 

 m

 s

2 s



In Example 6.7, the mass, energy, and entropy rate balances are used to evaluate a per-

formance claim for a device to produce hot and cold streams of air from a single stream of

air at an intermediate temperature.

EXAMPLE 6.7 Evaluating a Performance Claim

An inventor claims to have developed a device requiring no energy transfer by work or heat transfer, yet able to produce hot

and cold streams of air from a single stream of air at an intermediate temperature. The inventor provides steady-state test data

indicating that when air enters at a temperature of 39C and a pressure of 5.0 bars, separate streams of air exit at temperatures

of 18C and 79C, respectively, and each at a pressure of 1 bar. Sixty percent of the mass entering the device exits at the lower

temperature. Evaluate the inventor’s claim, employing the ideal gas model for air and ignoring changes in the kinetic and po-

tential energies of the streams from inlet to exit.

❶

6.6 Entropy Rate Balance for Control Volumes 235