Михалевська Т.В., Ісаєнко В.М., Гроза В.А. Основи статистичного обліку і банки інформації в екології. НАУ-друк, 2009

Подождите немного. Документ загружается.

Якщо критерій Стьюдента більший за табличне значення, то кореля-

ційний зв’язок між досліджуваними явищами вважають доведеним. У про-

тивному разі висновки про вірогідність зв’язку між явищами сумнівні.

Комбінаційні аналітичні групування і дисперсійний аналіз можна

використовувати для вивчення зв’язку результативної ознаки з дво-

ма і більше факторними ознаками. Вони

дають можливість аналізу-

вати залежність результативної ознаки від кожного з факторів при

фіксованих значеннях інших. Методи вимірювання такого зв’язку і

перевірку його істотності називають багатофакторними дисперсій-

ними комплексами. Вони пов’язані з громіздкими розрахунками і

потребують використання спеціальних програмних продуктів.

КОНТРОЛЬНІ ПИТАННЯ

1. Які розрізняють види дисперсій?

2. У чому полягає суть правила додавання дисперсій?

3. Які статистичні критерії використовують для оцінки надійності ко-

реляційних характеристик?

4.5. Моменти варіацій

У статистиці широко використовують статистичні характеристи-

ки, що називаються моментами. Моменти поділяють на початкові і

центральні. Початковим моментом і-го періоду ознаки статистичної

сукупності називається середня арифметична і-го ступеня значень

ознак статистичної сукупності. Початковий момент першого поряд-

ку — це середня арифметична величина. Центральним моментом і-

го періоду ознаки статистичної сукупності

називається середня ариф-

метична і-го ступеня відхилень розмірів ознак сукупності від її се-

реднього значення. Формули для обчислення моментів варіації на-

ведено у табл. 4.4.

Таблиця 4.4

МОМЕНТИ ВАРІАЦІЇ

Момент варіації Для незгрупованих даних Для згрупованих даних

Початковий

α=

∑

α=

∑

Центральний

()

−

∑

()

yyf

−

∑

КОНТРОЛЬНІ ПИТАННЯ

1. На які типи поділяють моменти варіації?

2. У чому полягає відмінність між початковими і центральними момен-

тами варіації?

4.6. Характеристики форми розподілу

Формою розподілу статистичної сукупності називають криву

співвідношення частот і значень варіюючої ознаки. За своєю фор-

мою розподіли поділяють на одно-, дво- і багатовершинні. Наяв-

ність двох і більше вершин свідчить про неоднорідність сукупності,

про поєднання у ній груп із різними рівнями ознаки. Розподіли якіс-

но однорідних сукупностей, як правило, одновершинні. Серед

одно-

вершинних розподілів розрізняють симетричні й асиметричні (ско-

шені), гостро- і плосковершинні.

У симетричному розподілі рівновіддалені від центра значення

ознаки мають однакові частоти, а в асиметричному — вершина змі-

щена. Напрям асиметрії протилежний напряму зміщення вершини,

тобто, якщо вершина зміщена вліво, то це правостороння асиметрія,

і навпаки.

Найпростішою мірою асиметрії форми

розподілу є відхилення

моди від середнього арифметичного або відхилення медіани від се-

реднього арифметичного значення ознаки. Для правосторонньої

асиметрії виконується умова:

Me Mo>>

а для лівосторонньої:

Me Mo<<

У симетричному розподілі характеристики центра (мода, медіа-

на, середнє арифметичне) мають однакові значення.

Розглянемо два методи оцінки асиметрії.

Перший метод полягає в оцінці асиметрії за допомогою статис-

тичних характеристик положення.

Асиметрія визначається як без-

розмірна статистична характеристика, що дорівнює відношенню різ-

ниці середнього значення і медіани чи моди і середнього квадратич-

ного відхилення:

−

або

−

Ці статистичні характеристики при симетричному розподілі до-

рівнюють нулю. При правосторонній асиметрії виконується умова

0AA>>.

При лівосторонній асиметрії маємо співвідношення

0AA<<.

Другий метод полягає в оцінюванні

коефіцієнта асиметрії,

який дорівнює стандартизованому моменту третього порядку:

A =

З використанням цієї характеристики при симетричному розподілі

0A = , при правосторонній асиметрії

0A > , при лівосторонній —

0A < .

Для характеристики крутості кривої форми розподілу використо-

вують ексцес.

Ексцес — це статистична безрозмірна величина, яка характери-

зує форму кривої розподілу і дорівнює різниці стандартизованого

моменту четвертого порядку статистичної сукупності і стандартизо-

ваного моменту четвертого порядку нормального розподілу.

Для нормального розподілу стандартизований момент четвертого

порядку дорівнює трьом. Отже, ексцес обчислюється за формулою:

()

3, де .

−

=− =

∑

Зрозуміло, що для нормального розподілу ексцес дорівнює нулю.

Якщо

Е > 0, то вершина кривої розподілу розташована вище верши-

ни кривої нормального розподілу і форма розподілу називається го-

стровершинною, і навпаки, якщо

E < 0, то вершина кривої розподілу

розташована нижче кривої розподілу нормального закону і форма

розподілу називається плосковершинною.

КОНТРОЛЬНІ ПИТАННЯ

1. Якими показниками характеризують форми розподілу?

2. Що таке ексцес?

3. Як за значенням ексцесу визначити форму розподілу?

4.7. Нормальний розподіл

Найпоширенішим у статистиці є нормальний розподіл. За норма-

льним законом розподілені зріст людини, висота окремого дерева у

лісі, похибка при вимірюванні якості повітря та багато інших явищ,

у яких проявляється велика кількість незалежних значень спостере-

жуваних ознак, серед яких немає суттєво відмінних від решти зна-

чень ознаки статистичної сукупності.

Ознака статистичної

сукупності називається розподіленою за но-

рмальним законом з параметрами

(, )x σ , якщо її щільність ймовір-

ності (або диференціальна функція) має вигляд

()

() ,

fx e

−

σπ

де

— оцінки відповідно середнього значення і середнього квад-

ратичного відхилення спостережуваних ознак статистичної сукупності.

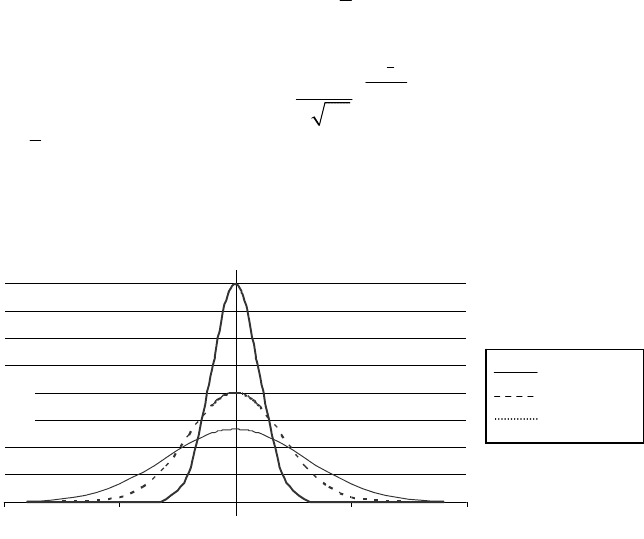
Графік щільності ймовірності функції нормального розподілу на-

зивають нормальною кривою (або кривою Гаусса) (рис. 4.1).

-0,05

0,05

0,1

0,15

0,2

0,25

0,3

0,35

0,4

0,45

0-5 0 5 1

f(x)

–

Крива Гаусса

(f)х

sigma = 1

sigma = 2

sigma = 3

Рис. 4.1. Крива Гаусса для різних значень середнього

квадратичного відхилення

Властивості графіка щільності ймовірностей нормального закону

розподілу:

1. Площа, яка обмежує графік щільності ймовірностей та вісь Oх,

дорівнює одиниці:

() 1

xdx

+∞

−∞

∫

2. Графік симетричний відносно прямої

, форма графіка за-

лежить від значення параметра

, а положення визначається пара-

метром

. У точці

= функція досягає максимального значення,

а в точках

x ±σ знаходяться точки перегину графіка.

3. Якщо ознака статистичної сукупності розподілена за нормаль-

ним законом, то ймовірність того, що випадкова величина відхи-

литься від математичного сподівання не більше ніж на

3σ

, дорівнює

0,9973 (правило трьох сигм).

Крім нормального, в теорії розглядається ряд інших розподілів, які є

об’єктом вивчення теорії ймовірностей та математичної статистики.

КОНТРОЛЬНІ ПИТАННЯ

1. Який статистичний розподіл називають нормальним?

2. Які властивості має графік щільності ймовірностей нормального

закону розподілу?

3. Якими параметрами визначається форма кривої Гаусса?

4.8. Критерії згоди

При розв’язуванні екологічних задач часто необхідно встанови-

ти, за яким законом розподілена ознака статистичної сукупності, що

відповідає досліджуваному явищу. Для відповіді на це питання ви-

користовують так звані критерії згоди.

Критерієм згоди називається статистичний критерій, який використо-

вується для з’ясування розбіжностей між прийнятою статистичною мо-

деллю і спостережуваними даними

ознаки, які має описати дана модель.

Одним із найбільш поширених є критерій згоди Пірсона

(хі-

квадрат), який полягає у наступному.

Нехай в результаті незалежних спостережень ознаки статистич-

ної сукупності χ зафіксовані значення

, ,...,

xx.

Вводиться гіпотеза

, яка полягає у тому, що спостережувана

ознака статистичної сукупності має закон розподілу ()

x . Викорис-

товуючи критерій згоди

, необхідно з’ясувати, чи узгоджується із

заданою надійністю Р прийнятий закон розподілу спостережуваної

ознаки статистичної сукупності. Інакше кажучи, чи можна із зада-

ною надійністю Р вважати гіпотезу

правильною.

Нехай

— частота варіанти ,1, 2,...,,

in=

∑

— загаль-

не число спостережень. На основі спостережуваних даних ознаки

обчислюються оцінки параметрів прийнятого закону розподілу

()

x . Після визначення передбачуваного теоретичного закону роз-

поділу обчислюють ймовірність подій

{

}

,1, 2, ..., .

PPXxi n===

Теоретичну частоту варіанти

, 1, 2,...,

in=

, обчислюють за фо-

рмулою

′

Якщо теоретичні

′

і спостережувані частоти

суттєво відріз-

няються, то гіпотеза

відкидається, і навпаки, якщо ці значення

мало відрізняються, то гіпотеза

приймається. Як міра відміннос-

ті частот обчислюється розрахункове значення критерію Пірсона

()

′

−

χ=

′

∑

Для застосування критерію Пірсона необхідно, щоб загальне чи-

сло дослідів

n було достатньо велике. На практиці число дослідів

вважається достатнім, якщо

50≥n , а спостережувані частоти не

менше п’яти.

Фактичне (розрахункове) значення

порівнюють з критичним

(табличним). Для критичних значень

складені таблиці. Критичні

значення

знаходять з таблиць із заданою довірчою ймовірністю

Р і ступеням вільності l . Число ступенів вільності знаходять за фор-

мулою

1lnr=−−, де n — число інтервалів (груп), r — число

параметрів у законі розподілу, який береться за модельний.

Якщо при порівнянні розрахункового і критичного значень кри-

терію Пірсона виявляється, що

(, )

lPχ<χ , то з заданою надійніс-

тю Р можна вважати, що прийнятий закон розподілу узгоджується із

законом розподілу спостережуваної ознаки статистичної сукупності.

Гіпотеза

приймається. У випадку

(, )

l Pχ>χ нульову гіпотезу

слід відхилити.

КОНТРОЛЬНІ ПИТАННЯ

1. У яких задачах використовують критерії згоди?

2. У чому полягає критерій згоди Пірсона?

3. Які частоти використовуються для розрахунку критерію Пірсона?

5.1. Поняття вибіркового спостереження.

Причини й умови його застосування

Статистичне спостереження за охопленням одиниць обстеження

сукупності поділяють на суцільне і несуцільне. З усіх видів несуціль-

ного спостереження в практиці статистичних досліджень найбільше

визнання і застосування дістало вибіркове спостереження.

Вибіркове спостереження — це такий вид несуцільного спосте-

реження, при якому досліджуються не всі елементи сукупності, що

вивчається, а лише певним чином відібрана їх частина. Сукупність, з

якої вибирають елементи для обстеження, називають генеральною, а

сукупність, яку безпосередньо обстежують, — вибірковою. Статис-

тичні характеристики вибіркової сукупності розглядаються як оцін-

ка відповідних характеристик генеральної сукупності.

Безумовно, що суцільне спостереження забезпечує найбільш пов-

ну інформацію про загальну кількість одиниць, про середні і віднос-

ні показники досліджуваної сукупності. Однак на практиці є чимало

випадків, коли суцільне спостереження недоцільне або зовсім не-

можливе. При вивченні певного кола екологічних явищ вибіркове

спостереження єдино можливе. Практика вибіркових спостережень

досить різноманітна. Це, наприклад, дослідження забруднень окре-

мих ділянок, земельних угідь, вивчення громадської думки, екологіч-

на експертиза окремих підприємств галузі. Інколи вибіркове спосте-

реження поєднується із суцільним. Крім того, вибірковий метод ви-

користовують для прискореної обробки матеріалів суцільного спо-

стереження та перевірки правильності даних переписів і одноразо-

вих обстежень. До вибіркового спостереження статистика вдається у

випадках, коли треба у стислі терміни та з мінімальними затратами

праці і коштів одержати кількісні характеристики досліджуваної

сукупності або коли не можна чи недоцільно здійснювати суцільне

спостереження.

Таким чином, основні причини, що зумовлюють перевагу вибір-

кового методу, зводяться до такого:

• економія часу і коштів;

• зведення, до мінімуму псування або можливе знищення дослід-

жуваних об’єктів;

ВИБІРКОВЕ СПОСТЕРЕЖЕННЯ

РОЗ

ІЛ

• необхідність поглибленого вивчення кожної одиниці спосте-

реження при неможливості дослідити за такою програмою всі оди-

ниці сукупності;

• досягнення більшої точності результатів дослідження завдяки

скороченню помилок, що мають місце при реєстрації;

• застосування вибіркового спостереження як засобу контролю

даних суцільного спостереження.

Вибірковий метод дає змогу через вивчення частини спеціально

відібраних одиниць охарактеризувати масове явище в цілому. Тео-

рія і практика вибіркового спостереження показує, що воно за умови

правильної організації дає достовірні відомості, цілком придатні для

практичного використання. Науковим обґрунтуванням можливості

застосування вибіркового спостереження є діалектична єдність оди-

ничного, особливого і загального, згідно з якою в кожному одинич-

ному наявні риси особливого і загального, а загальне має риси оди-

ничного і особливого. Це дає змогу за одиничним і особливим суди-

ти про загальне, за частиною — про ціле, якщо правильно знайдено

зв’язок між ними.

Основними етапами вибіркового спостереження є:

♦ обґрунтування мети вибіркового спостереження;

♦ складання програми спостереження і розробка відповідних даних;

♦ вирішення організаційних питань щодо спостереження;

♦ визначення частки і способу відбору одиниць у вибіркову су-

купність;

♦ здійснення відбору;

♦ реєстрація ознак досліджуваних одиниць;

♦ узагальнення даних спостереження та визначення вибіркових

характеристик;

♦ обчислення похибок вибірки;

♦ поширення кількісних характеристик вибіркового спостере-

ження на всю сукупність.

Переваги вибіркового спостереження над суцільним реалізують-

ся лише при дотриманні наукових принципів його організації і про-

ведення, насамперед неупередженого, випадкового вибору елементів

для обстеження. Принцип випадковості відбору забезпечує всім еле-

ментам генеральної сукупності рівні можливості потрапити у вибірку.

Так, якщо генеральна сукупність містить N елементів, а для об-

стеження треба відібрати п, то число можливих вибірок можна об-

числити за формулою комбінаторики:

!( )!

nN n

−

Усі вони мають однакову ймовірність 1

C , а кожна з них несе в

собі певну похибку, що відображає факт випадковості вибору. Оскіль-

ки вибіркова сукупність не точно відтворює склад генеральної сукуп-

ності, то й вибіркові оцінки не збігаються з відповідними характе-

ристиками генеральної сукупності. Розбіжності між ними називають

помилками (похибками) репрезентативності. Так, для середньої

величини вона являє собою різницю між генеральною і вибірковою

середніми, для частки — між генеральною і вибірковою частками,

для дисперсії — відношення генеральної і вибіркової дисперсій тощо.

Точність результатів вибіркового спостереження залежить від

способу відбору одиниць, ступеня коливання ознаки в сукупності та

від кількості відібраних одиниць.

КОНТРОЛЬНІ ПИТАННЯ

1. Яке спостереження називають вибірковим?

2. У чому полягають переваги вибіркового спостереження?

3. Які основні етапи вибіркового спостереження?

5.2. Методи і способи відбору одиниць у вибіркову сукупність

Формування вибірки — не безладний процес, він здійснюється за

певними правилами. Насамперед визначають основу вибірки. Залеж-

но від специфіки об’єкта одиницею основи вибірки можуть бути

окремі одиниці (індивідуальний відбір) або якісно однорідні групи

(серії) досліджуваних одиниць (груповий відбір), або комбінація

індивідуального і групового відбору.

Від основи вибірки залежить спосіб відбору елементів сукупнос-

ті для обстеження. Найчастіше використовують такі спо

соби відбору:

простий випадковий, систематичний (механічний), типовий (райо-

нований), серійний.

Простий випадковий відбір полягає в тому, що вибіркова сукуп-

ність утворюється в результаті випадкового неупередженого відбору

окремих одиниць із генеральної сукупності. При цьому кількість

відібраних у вибіркову сукупність одиниць визначається на основі

прийнятої частки (питомої ваги) вибірки.

Важливою умовою репрезентативності простого випадкового

відбору є те, що кожна одиниця генеральної сукупності має однакові

можливості потрапити до вибіркової сукупності. Саме принцип ви-

падковості потрапляння кожної одиниці генеральної сукупності у

вибірку запобігає виникненню систематичних (тенденційних) помилок

100

вибірки. Формування простої випадкової вибірки може здійснюва-

тися жеребкуванням або за допомогою таблиць випадкових чисел.

Систематичний (механічний) відбір передбачає, що основою

вибірки є упорядкована чисельність елементів сукупності. Вибір

елементів здійснюється через рівні інтервали. Крок (розмір) інтер-

валу обчислюють діленням обсягу сукупності N на передбачений

обсяг вибірки п. Початковий елемент відбору визначають як випад-

кове число у першому інтервалі елементів сукупності, другий еле-

мент залежить від початкового числа і кроку інтервалу. Наприклад,

для 5 %-ї вибірки кроком інтервалу є число

10,05 20Nn==

. Тоб-

то у вибірку має потрапити кожний двадцятий елемент. Якщо поча-

тковий елемент — випадкове число 7, то другий елемент становить

7 + 20 = 27, третій — 27 + 20 = 47 тощо. Таким чином, відповідно до

прийнятої частки вибірки генеральна сукупність механічно розбива-

ється на рівні групи і з кожної такої групи у вибірку потрапляє лише

один елемент.

Типова, або районована, вибірка організовується таким чином:

генеральна сукупність розбивається на однорідні типові групи, ра-

йони, дільниці за певною ознакою, а потім з кожної такої групи від-

бирається певна кількість одиниць спостереження, пропорційно пи-

томій вазі групи у генеральній сукупності. Перевагою типової вибір-

ки є те, що, створюючи групи і відбираючи з них певну кількість

одиниць спостереження, у неї потраплять представники різних ти-

пових груп і вибіркові характеристики, визначені на їх базі, будуть

максимально наближені до генеральних характеристик. Вибірка стає

вірогіднішою.

Серійна вибірка (гніздова) полягає в тому, що відбираються не

окремі одиниці, а цілі групи (серії, гнізда) випадковим або механіч-

ним методом. У відібраних серіях обстежують всі одиниці без винят-

ку, а результати поширюють на всю сукупність.

Вибірка елементів для вибіркового спостереження може здійс-

нюватися способом повторного і безповторного відбору.

Повторним відбором називають такий відбір, при якому кожна

обстежувана одиниця знову повертається до генеральної сукупності,

продовжує брати участь у подальшому відборі і може потрапити

повторно у вибірку для обстеження.

Безповторним називається такий відбір, при якому один раз описані

одиниці спостереження у подальшому відборі участі не беруть. Безпов-

торний відбір, як правило, дає точніші результати, ніж повторний.

Як відомо із математичної статистики, всі види відбору (крім ме-

ханічного) можуть бути повторними і безповторними. Механічний

відбір завжди безповторний.