Middleton W.M. (ed.) Reference Data for Engineers: Radio, Electronics, Computer and Communications
Подождите немного. Документ загружается.


47-20
x-xo
y-yo
2-20
x1
-
xo
y,
-
yo
z,
-
zo
x2
-no
Y2 -Yo
22
-
zo
REFERENCE
DATA
FOR ENGINEERS
=
0
t‘
Fig.
20.
Coordinates
of
point
P.
proportional to the direction cosines are called direction
numbers.
Distance Between
Two
Points
where,
A,
B,
and
C
are the direction numbers
of
a normal
(xl,
y,,
z,)
is
a point on the plane.
Normal Form.
to the plane,
x
cosa
+
y
cosp
+
z
cosy
-
p
=
0
where,
cosa, cosp, and cosy
are
the direction cosines
of
a
p
is the distance
of
the plane to the origin.
normal to the plane,
Equations
of
a Straight Line
Point-Direction Form:
x
=
At
+
XI
or
y
=
Bt
+
y,
z
=
Ct
+
z,
(parametric)
where,
A,
B,
and
C
are direction numbers
of
the line,
(x,,
y1
,
zl)
is a point on the line.
Two-Point Form:
(x
-
Xl)/(Xl
-
no)
=
(Y
-
YlY(Y1
-
Yo)
=
(2
-
Z1)/(Z]
-
zo)
or
x
=
no
+
(x,
-
xo)t
Y
=
Yo
+
(Y1
-
Y0)t
z
=
zo
+
(zl
-
zo)t
(parametric)
where
(xo
,
yo,
zo)
and
(xl
,
y
I
,
z
are two points on the
line.
Ellipsoid
(x2/a2)
+
(y2/b2)
+
(z2/c2)
=
1
where
a,
b,
c
are
the semiaxes
of
the ellipsoid or the
intercepts on the
x,
y,
and
z
axes, respectively.
Prolate Spheroid
a2(y2
+
z2)
+
b2x2
=
a2b2
where
a
>
6,
and x-axis
=
axis
of
revolution.
Oblate Spheroid
b2(x2
+
z2)
+
a2y2
=
a2b2
where
a
>
6,
and y-axis
=
axis
of
revolution.
Paraboloid
of
Revolution
y2
+
22
=
2px
x-axis
=
axis
of
revolution

MATHEMATICAL EQUATIONS
47-21
Hyperboloid of Revolution
Revolving an x-hyperbola about the x-axis results in
the hyperboloid of two sheets
a2(y2
+
z2)
-
b2x2
=
-a2b2
Revolving an x-hyperbola about the y-axis results in the
hyperboloid of one sheet
b2(x2
+
2')
-
a2y2
=
a2b2
DIFFERENTIAL CALCULUS
List of Derivatives
In
the following,
u,
v,
w
are differentiable functions
of
x,
and c is
a
constant.
General Equations:
dcldx
=
0
dx/dx
=
1
(d/dx)(u
+
v
-
w)
=
(du/dx)
+
(dv/dx)
-
(dw/dx)
(d/dx)(cv)
=
c(dv/dx)
(d/dx)(uv)
=
u(dv/dx)
+
v(du/dx)
(d/dx)(VC)
=
cvc-
'
(dvldx)
dxv
V2
d
(!)
-
-
v(du/dx)
-
u(dv/dx)
dyldx
=
(dy/dv)(dv/dx),
dyldx
=
(dn/dy)-'
,
if y
=
y(v)
if dxldy
#
0
Transcendental Functions:
(~/G!x)
Inv
=
v-l
(dv/dx)
(d/dx)
(c")
=
c'lnc(dv/dr)
(d/dn)
(e")
=
e"(&/&)
(d/dx)
(u")
=
vuy-'(du/dx)
+
(Inu)u'(dv/dx)
(dldx)
(sinv)
=
cosv(dv/dx)
(dldx)
(cosv)
=
-sinv(dv/dx)
(~x)
(tanv)
=
sec2v(dv/dx)
(dldr)
(cotv)
=
-csc2v(dv/dx)
(d/dx)
(secv)
=
secv tanv(dv/dn)
(d/dn)
(cscv)
=
cscv cotv(dv/dx)
(d/dx)
(arc sinv)
=
(1
-
v2)-li2(dv/dx)
(dldx)
(arc cosv)
=
-(1
-
v2)-1/2(dv/dx)
(dldx)
(arc tanv)
=
(1
+
v2)-'(dv/dx)
(d/dx)
(arc cotv)
=
-(1
+
vZ)-'(dv/dx)
(d/dx)
(arc secv)
=
[v(v2
-
1)1'2]-t(dv/~)
(d/dx)
(arc cscv)
=
-[v(v2
-
1)'/2]-l(dv/dx)
(d/d-x)
(sinhv)
=
coshv(dv/dx)
(dldx)
(coshv)
=
sinhv(dv/dx)
(d/dx)
(tanhv)
=
sech2v(dv/dx)
TABLE OF INTEGRALS
lndef inite Integrals
Jaf(x)dx
=
a/h&
General Equations:
IMX)
+
g(n)ldx
=
IJ
f(x)dx
+
gwx
Elementary
Forms:

47-22
REFERENCE
DATA
FOR ENGINEERS
=
In
1x1
ex
dx
=
ex
I
s
i
I
I
I
lnxh
=
x
lnx
-
x
sinxdx
=
-cosx
cosndx
=
sinx
tdx
=
-In /cosxI
cotxdx
=
In Isinxl
cscxb
=
In Itan$
I
I
secndx
=
In lsecx
+
tam1
sinhxdx
=
coshx
I
coshxdx
=
sinhx
I
cschxdx
=
In /tanhixi
s
/dx/(l
-
x2)
=
In
[(l
+
x)/(l
-
x)]
Ixdx/(an
+
b)’
=
a-’[b/(ax
+
b)
+
In
(an
+
b)]
Idx/[x(ax
+
b)]
=
b-’ In
[x/(an
+
b)]
Idx/[x(an
+
b)‘]
=
[b(an
+
Idx/[x2(ax
+
b)]
=
-(bx)-’
+
(a/b2)
In
[(a
+
b)/x]
+
b-2
In
[x/(ax
+
b)]
,/d~/[x’(ax
+
b)21
=
-(2ax
+
b)/[bzx(ax
+
b)]
+
(2a/b3)
In
[(ax
+
b)/x~

MATHEMATICAL EQUATIONS
47-23
/xm(ax
+
b)"dx
=
[,"+'(ax
+
b)"/(m
+
n
+
l)]
+
[bn/(m
+
n
+
l)] xm(a
+
b)"-'dx
I
Forms
Containing
(ax
+
b)'",
a
#
0,
b
#
0:
2(3ax
-
2b)[(ax
+
b)3]1i2
15a2
Ix(ax
+
b)l/2h
=
I
/xm(ax
+
b)1'2dx
=
[2/a(2m
+
3)]
xm[(ax
+
b)3]1i2
-
mb
xm-l(a
+
b)'/'h
I
dx
=
2(ax
+
b)'"
+
(b)'"
In
(ax
+
b)'I2
-
(b)"'
1
,
,
1
(ax
+
b)
'I2
+
(b)
'I2
=
[2/(-b)"2]tan-1[(ax
+
b)/-b]"',
b
<
0
_-
(ax
+
b)'l2
-
(2n
-
3)a
I
dx
nZ1
(n
-
I)w-'
(2n
-
2)b ~"-'(ax
+
b)l"'
Forms
Containing
R
=
ax2
+
bx
+
c, a
#
0,
x
>
0:
Let
q
=
4ac
-
b2
1:
=
[2/(q)1/2~tan-l[(2ax
+
b)/(q)1/21,
q
>
o
2ax
+
b
-
(-q)"2
=
(4-1/2
In
<O
2ax
+
6
+
(-q)'I2'
(If
q
=
0,
R
is
a
perfect
square.)

47-24
REFERENCE
DATA
FOR ENGINEERS
Xm-l
(2n
-
m
-
l)aR"-'
2n-m-1
-
(bla)
I
Gdx
R
+
-
2n
-
m
-
1
Forms Containing (R)'"
=
(ax2
+
bx
+
c)'",
a
#
0:
Let
q
=
4ac
-
b2
dx
-
2(2ax
+
b)(R)'/2
./m
-
(2n
-
l)qRn
xmRn
(2n
+
m)a
-
(2n
+
2m
-
3)b dx
2c(m
-
1)
I
x"-IR"(R)~/~
-
(R)
=-
dx
(m
-
l)cxm-'R"
Logarithmic
Integrands
lnaxdx
=
x(1nux
-
1)
I
I
logbxdx
=
log,e(lnx
-
l)x
=
[(lnx
-
l)x/lnb]

MATHEMATICAL EQUATIONS
47-25
Ix"(1nx)"dx
=
[xmt'(lnx)"/(m
+
l)]
-
[n/(m
+
l)]
xm(lnx)"-]d~,
m
#
-1
I
I[(lnx)"/x]dx
=
(lnx)"+'/(n
+
l),
n
#
-1
/(xm/lnx)dx
=
Ei[(n
+
l)lnx],
m
#
-1
Exponential Integrands
Iubxh
=
abx/(blna)
!dx/(a
+
bemx)
=
(x/a)
-
(am)-'
lnla
+
bemi,
a
and
m
#
0
mx
1/2
-
(a)
112
112
-1
In(a
+
be
a>o
dx
I
+
bemx)1/2
=
1
(a
+
bemx)l"
+
(a)"'
'
Trigonometric Integrands
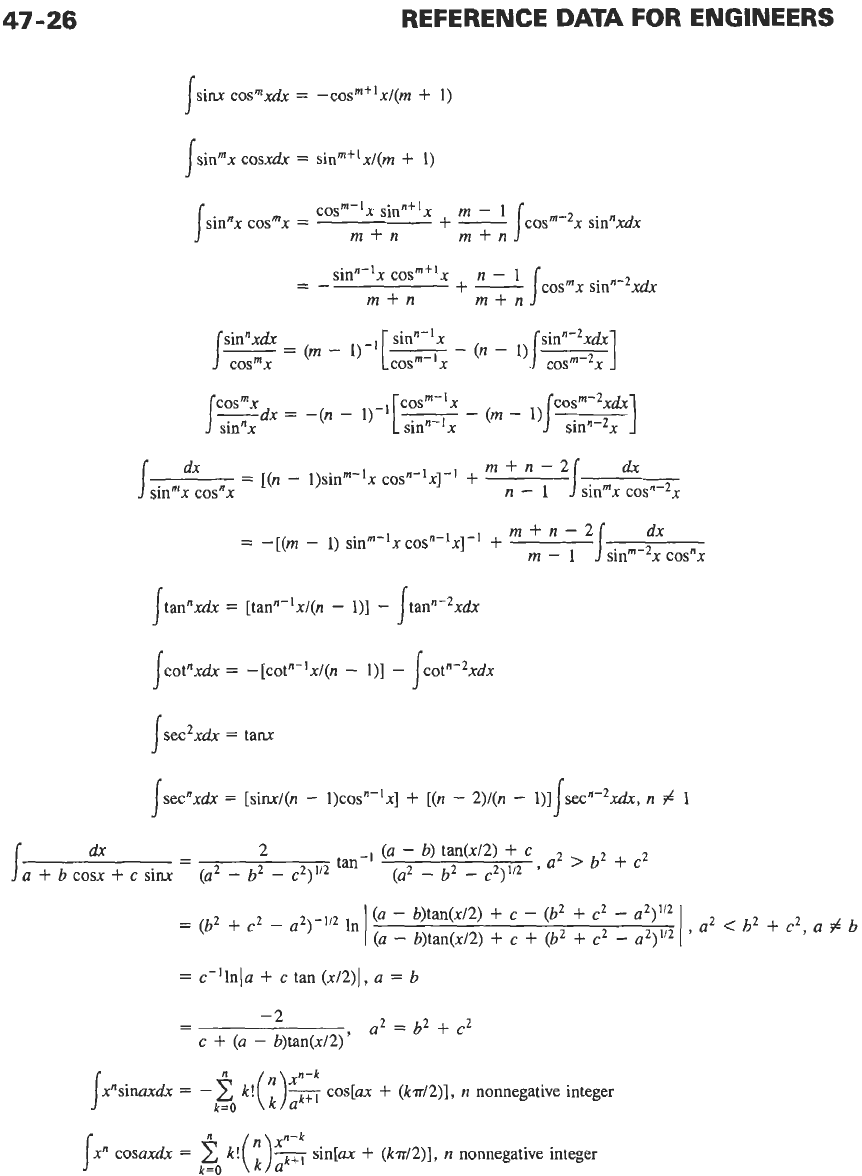
47-26
REFERENCE
DATA
FOR ENGINEERS
sinr cosmxdx
=
-cosm+'x/(m
+
1)
I
dx
m
-
1
I
sinm-2x cosnx
m+n-2
=
-[(m
-
1)
sinm-lx
COS"-'XI-~
+
tan"xdx
=
[tan"-'x/(n
-
I)]
-
tan"'xdx
I
I
I
I
cot"xdx
=
-[cot"-'x/(n
-
l)]
-
cot"-2xdx
sec2x&
=
tam
I
Isecnxdx
=
[sinr/(n
-
l)cos"-'x]
+
[(n
-
2)/(n
-
111
sec"2xdx,
n
z
1
I
,
(a
-
b) tan(x/2)
+
c
,
a2
>
b2
+
c2
(a
-
b)tan(x/2)
+
c
-
(b2
+
c2
-
a
u2
(a
-
b)tan(x/2)
+
c
+
(b2
+
c2
-
u2)1/2
(a2
-
b2
-
c2)1/2
tan
-
2
- -
dx
/a
+
b
cosx
+
c
sim (a2
-
b2
-
c2)'12
)
1,
u2
<
b2
+
c2,
a
#
b
=
c-'ln)a
+
c
tan (x/2)1,
a
=
b
-2
c
+
(a
-
b)tan(x/2)'
a2
=
b2
+
c2
- -
cos[ax
+
(k?r/2)],
n
nonnegative integer
k=O
Ix"
cosaxdx
=
2
k!
sin[ax
+
(k.rr/2)],
n
nonnegative integer
k=O

MATHEMATICAL
EQUATIONS
47-27
inverse Trigonometric Integrals,
x
and
a
>
0:
/sin-l(x/a)dx
=
x sin-l(x/a)
+
(a2
-
x2)~'2
x sin-lxdx
=
a[(2x2
-
I)sin-'x
+
x(l
-
x2)112]
I
x cos-lxdx
=
$[(2x2
-
l)cos-'x
-
x(1
-
X2)1'*]
I
/x"sin-'xdx
=
[x"+'sin-'x/(n
+
l)]
-
(n
+
l)-l
[xntl/(l
-
x2)li2]dx
I
Miscellaneous integrals:
+
~'3
arc tan
-
xv3
1,
p
=
@/a)
1'3
___
dx
=
E[;
In
(x
+
PI2
Lx3
+
b
3b
x2 -px
+p2
2p
-
x
Definite Integrals
I,'
XYI
-
Xydx
=
mu
+
i)qV
+
i)/ryU
+
+
2)1,
>
-1,
>
-1
=
[u!v!/(u
+
v
+
l)!],
if
u,
v
nonnegative integers
Jb"
x"dx/(l
+
x")
=
(dv)
csc[(u
+
l).rr/v],
0
<
u
+
1
<
v

47-28
REFERENCE
DATA
FOR ENGINEERS
1
X2ntldX
-
(2n)
(2n
-
2)
-
*
6.4.2
s
o
(1
-
x~)”~
(2n
+
1)
(2n
-
1)
.
5-3.1’
-
n positive integer
1
x2”dx
(2n
-
1)
(2n
-
3)
*
. .
5.3.1
I
-
-
*
~r,
n
positive integer
I
0
(1
-
xy
(24
(2n
-
2)
.
6.4.2
Jb”
xbe-nxdx
=
r(b
+
l)/abt’,
b
>
-1,
a
>
0
=
b!/ab+’,
b
nonnegative integer
exp[-(ax2
+
bx
+
c)]&
=
f(~/a)”~
exp[(b2
-
4ac)/4a][1
-
erf(ib~”~)]
(sinmx/x)dx
=
ir,
rn
>
0
=O,m=O

MATHEMATICAL EQUATIONS
47-29
I'
[Inxl(l
-
x)]dx
=
-:v*
SERIES
Taylor's Series for a Single Variable
f(z)
=
f(a)
+
f'(u)
(Z
-
U)
+
i[f"(~)]
(Z
-
=
(k!)-lf@'(a)
(Z
-
+
R,
+
. .
+
[f(')(~)/n!]
(Z
-
a)"
+
R,
n
k=O
where the remainder is bounded
by
lR,I
5
[M/(n
+
l)!]
Iz
-
a/""
in which
M
=
max
orea
[a
+
Nz
-
u)Il
If a,
z,
andfare real, then there exists a real
8,
0
<
0
<
1,
such that the remainder
is
R,
=
cf"tl)[a
+
e(z
-
a)]/(n
+
l)!}
(Z
-
a)""
When
a
=
0,
this series is often called MacLaurin's series.
