Middleton W.M. (ed.) Reference Data for Engineers: Radio, Electronics, Computer and Communications
Подождите немного. Документ загружается.


46-26
REFERENCE
DATA
FOR ENGINEERS
10.
Lee, W.
C.
Y.
“Overview
of
Cellular CDMA.”
IEEE Transactions
on
Vehicular Technology.
Spe-
cia1 issue
on
digital cellular, May
1992.
11.
Lee, W. C.
Y.
Mobile Communications Design
Fundamentals.
1st
ed. Indianapolis: Howard W.
Sams
&
Co.,
1986.
2nd ed. New York:
John
Wiley
&
Sons,
hc.,
1993.
12.
Lee, W.
C.
Y.
Mobile Cellular Telecommunica-
13.
Lee,
w.
c.
Y.
Mobile Communications Engineer-
14.
Lee, W. C.
Y.
Lee’s Essentials
of
Wireless Commu-
tions,
2nd ed. McGraw-Hill,
1995.
ing,
2nd ed. McGraw-Hill,
1998.
nications.
McGraw-Hill, 2001.

47
Mat
hematical
Equations
Mensuration Equations
47-4
Areas and Lengths Associated With Plane Figures
Surface Areas and Volumes
of
Solid Figures
Algebraic and Trigonometric Equations (Including Complex
Quantities)
47-6
Quadratic Equation
Solution
of
Cubic Equations
Solution
of
Quartic Equations
Complex Quantities
Properties
of
e
Properties
of
Logarithms
Sums
Combinations and Permutations
Bernoulli Numbers
Trigonometric Identities
Approximations for Small Angles
Inequalities
Plane Trigonometry
47-11
Right Triangles
Oblique Triangles
Spherical Trigonometry
47-12
Right Spherical Triangles
(y
=
90")
Oblique Triangles
Hyperbolic Functions
47-13
Hyperbolic Trigonometry
47-14
Conformal Model
Projective Model
Right Hyperbolic Triangles
(y
=
90")
Oblique Hyperbolic Triangles
47-1

47-2
REFERENCE
DATA
FOR
ENGINEERS
Plane Analytic Geometry
47-16
Straight Line
Transformation
of
Rectangular Coordinates
Circle
Parabola
Ellipse
Hyperbola
Solid Analytic Geometry
47-19
Coordinates
Direction Cosines and Numbers
Distance Between Two Points
Equations of a Plane
Equations of a Straight Line
Ellipsoid
Prolate Spheroid
Oblate Spheroid
Paraboloid
of
Revolution
Hyperboloid
of
Revolution
Differential Calculus
47-21
List
of
Derivatives
Table
of
Integrals
47-21
Indefinite Integrals
Logarithmic Integrands
Exponential Integrands
Trigonometric Integrands
Definite Integrals
Series
47-29
Taylor’s Series for a Single Variable
Taylor’s Series for Two Variables
Miscellaneous Series
Matrix Algebra
47-31
Notation
Operations
Determinant
Linear Transformations
Eigenvectors and Eigenvalues
Further Definitions and Properties
Hermitian
Forms

MATHEMATICAL EQUATIONS
47-3
Vector-Analysis Equations
47-35
Rectangular Coordinates
Gradient, Divergence, Curl, and Laplacian in Coordinate Systems
Space Curves
Other Than Rectangular
Laplace Transform
47-38
Table of Laplace Transforms
47-38
General Equations
Miscellaneous Functions
Inverse Transforms
Selected Functions
47-39
Exponential Integrals
Cosine and Sine Integrals
Gamma Function
Psi and Polygamma Functions
Error Function
Fresnel Integrals
Elliptic Integrals
Bessel Functions
Orthogonal Polynomials
Numerical Analysis
47-43
Algorithms
for
Solving
F(x)
=
0
Algorithm for Solving
F(x,
y)
=
G(x,
y)
=
0
Interpolation Polynomial
Interpolation at Equidistant Points
Integration
Differentiation
Error in Arithmetic Operations
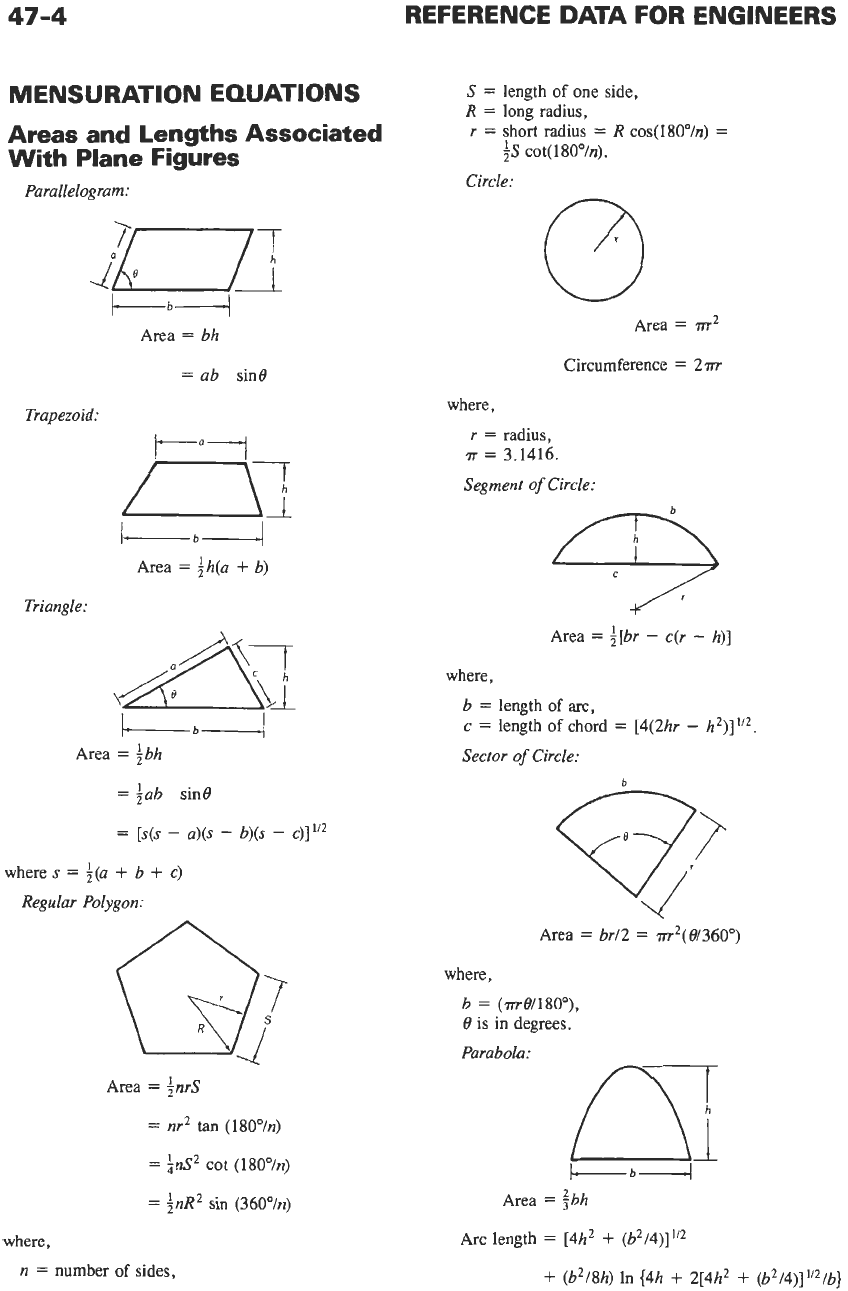
47-4
REFERENCE DATA FOR ENGINEERS
MENSURATION EQUATIONS
Areas and Lengths Associated
With
Plane Figures
Parallelogram:
+b*
Area
=
bh
=
ab
sin0
Trapezoid:
k.1
/-\T
S
=
length of one side,
R
=
long radius,
r
=
short radius
=
R
cos(180°/n)
=
Circle:
fS
cot(l8O0/n).
Area
=
m2
Circumference
=
2m
where,
r
=
radius,
7~
=
3.1416.
Segment
of
Circle:
LbI
Area
=
fh(a
+
b)
Triangle:
Area
=
f[br
-
c(r
-
h)]
I-b4
Area
=
fbh
=
fab
sin0
=
[s(s
-
a)(s
-
b)(s
-
c)]"~
where,
b
=
length
of
arc,
c
=
length of chord
=
[4(2hr
-
h2)]l/*.
Sector
of
Circle:
where
s
=
;(a
+
b
+
c)
Regular Polygon:
Area
=
br/2
=
m2(0/360")
where,
b
=
(me/isoo),
0
is in degrees.
Parabola:
Area
=
Inrs
=
nr2
tan (18Oo/n)
=
id2
cot (18O"ln)
=
;nR2
sin
(36O"ln)
where,
n
=
number
of
sides,
Area
=
ibh
Arc length
=
[4h2
+
(b2/4)]"2
+
(b2/8h)
In
(4h
+
2[4h2
+
(b2/4)]'/2/b}
MATHEMATICAL EQUATIONS
Ellipse:
t--.--I
Area
=
rab
Circumference
=
4aE(k)
where
E@)
is a complete elliptic integral with
k
=
(a2
-
b2)ll2/a
of the second kind,
a
>
b.
Trapezium:
Area
=
i[a(hl
+
h2)
+
bh,
+
ch2]
Surface Areas and Volumes
of
Solid Figures
Sphere:
Surface
=
4m2
=
12.5664r2
=
rd2
Volume
=
(4m3/3)
=
4.1888r3
Sector
of
Sphere:
Total surface
=
(m/2)(4h
+
c)
Volume
=
(2m2h/3)
=
2.0944r2h
=
(2m2/3)[r
-
(r2
-
ic2)1/2]
c
=
[4(2hr
-
h2)]’/2
Segment
of
Sphere:
Spherical surface
=
2mh
=
+
4h2)
47-5
Volume
=
rh2(r
-
fh)
=
rh2[(c2
+
4h2)/8h
-
ih]
c
=
[4(2hr
-
h2)]112
Cylinder:
Cylindrical surface
=
rdh
=
3.1416dh
Total surface
=
2m(r
+
h)
Volume
=
m2h
=
0.7854d2h
=
c2h/4r
=
0.0796c2h
c
=
circumference
Torus or Ring
of
Circular Cross Section:
--Id!-
Surface
=
4r2Rr
=
39.4784Rr
=
9.8696Dd
Volume
=
2r2Rr2
=
19.74Rr2
=
2.467Dd2
where,
D
=
2R
=
diameter to centers of cross-section of
r
=
d/2.
Pyramid:
torus,
Volume
=
Ah/3
When base is a regular polygon
Volume
=
4h{nr2[tan(36Oo/2n)]}
=
~h{~(ns2)[cot(36O0/2n)]}
where,
A
=
area
of
base,
n
=
number of sides,
r
=
short radius
of
base.
47-6
REFERENCE DATA FOR ENGINEERS
See “Regular Polygon” in subsection on plane figures.
Pyramidal frustum:
Volume
=
fk[a
+
A
+
(UA)”~]
where,
A
=
area of base,
a
=
area of top.
Cone With Circular Base:
Conical area
=
ms
=
m(r2
+
k2)”’
Volume
=
dk/3
=
1.047r2k
=
0.2618d2k
where
s
=
slant height.
Conic Frustum:
4
/------.
1
EY
Volume
=
(7rk/3)(R2
+
Rr
+
r2)
Area of conic surface
=
m(R
+
r)
Development of Conic Surface:
C
=
sR/(R
-
r)
0
=
360R/C
where
0
is
in degrees.
Wedge Frustum:
Volume
=
iks(a
+
b)
where
k
=
height between parallel bases.
Ellipsoid:
Volume
=
(4mbci3)
Surface
=
27i{c2
+
[b/(a2
-
~~)”~][c’F(+,k)
+
(a2
-
c2)E(+,k)]}
if
a
>
b
>
c
=
2~u{a
+
[c2/(a2
-
c~)“~]
x
In[a
+
(a2
-
C~)”~I/C}
(oblate ellipsoid)
if
a
=
b
>
c
=
27~c{c
+
&a2
-
c2)-112
arc sin[(a2
-
c
)
/all
if
a
>
b
=
c
(prolate ellipsoid)
F(+,
k)
and
E(+,
k)
are incomplete elliptic integrals
of the first and second kinds, respectively.
+
=
arc sin
[(a2
-
c2)1/2/a]
k
=
(u/b)[(b2
-
c2)/(a2
-
c
11
Paraboloid:
Volume
=
(m2k/2)
Curved surface
=
(.rrr/6k2)[(r2
+
4k2)3’2
-
r3]
ALGEBRAIC AND
TRIGONOMETRIC EQUATIONS
(INCLUDING COMPLEX
QUANTITIES)
Quadratic Equation
If
ax2
+
bx
+
c
=
0,
then
x
=
[-b
*
(b2
-
4ac)”2]/2a
=
2c/[-b
7
(b2
-
4ac)I’2]
Solution
of
Cubic Equations*
Given
z3
+
a2z2
+
alz
+
a.
=
0, let
13
a
,
r
=
(ala2
-
3ao)
-
g
az
q
=
Lal
-
+
z2.
*
Abramovitz,
M.
and Stegun,
I.
A.
Handbook
of
Mathe-
matical
Functions.
Washington.
D.
C.:
National
Bureau
of
Standards;
p.
17.

MATHEMATICAL EQUATIONS
47-7
If
q3
+
r2
>
0,
one real root and a pair of complex
q3
+
r2
=
0,
all roots real and at least two are
q3
+
r2
<
0,
all roots real (irreducible case)
conjugate roots
equal
Let
s1
=
[r
+
(q3
+
r2)112]113
s2
=
[r
-
(q3
+
r2)112]1’3
then
Solution
of
Quartic Equations*
Given
z4
+
a3Z3
+
a2z2
+
alz
+
a.
=
0,
find the
real root
u1
of the cubic equation
u3
-
a2u2
+
(ala3
-
4ao)U
-
(aI2
+
aoa32
-
4aoa2)
=o
and determine the four roots of the quartic as solutions
of the two quadratic equations
+
(UlI2)
T
[(u1/2)2
-
.oll’z
=
0
If
all roots of the cubic equation are real, use the
value of
uI
that gives real coefficients in the quadratic
equation.
Complex Quantities
In the following equations, all quantities are real
except
j
=
(-I)”~.
(A
+
jB)
+
(C
+
jD)
=
(A
+
C)
+
j(B
+
D)
(A
+
jB)(C
+
jD)
=
(AC
-
BD)
+
j(BC
+
AD)
A+jB AC+BD BC-AD
C+jD C2+D2 ‘jC2+D2
-=
-
*
Abramovitz,
M.
and Stegun,
I.
A.
Handbook
of
Mathe-
mafical
Functions.
Washington,
D.
C.:
National Bureau
of
Standards.
A B
A2
+
B2
-Jm
-- --
I
A
+
jB
Polar Form:
A
+
jB
=
p(cos0
+
j
sine)
=
pd8
De Moivre’s
Equation:
(A
+
jB)”
=
p”(cosv8
+
j
sinve)
where,
p
=
(A2
+
B2)112
>
0,
sine
=
Blp.
case
=
~/p,
For nonintegral v, this quantity is many-valued.
Complex Conjugate:
A
+
jB
=
(A
+
jB)*
=
A
-
jB
Analytic Function:
Let
f(z)
be a function of the
complex variable
z
=
x
+
jy.
Functionf(z) is analytic at
a point z
=
zo,
if
lim
[f(zo
+
Az)
-
f(zo)]/Az
Az-tO
exists independent of the manner in which
Az
ap-
proaches zero. Analyticity is equivalent to the existence
of a Taylor series about the point in question. In
addition,
f(z)
is analytic if and only if the Cauchy-
Riemann equations hold:
auiax
=
aviay
where,
u
=
Ref(z),
v
=
Imf(z).
Iff(z) is analytic for all
z,
it is called an entire function.
Properties
of
e
al
e
=
lim
(1
+
n-’)”
=
2
@!)-I
=
2.71828
e?jx
=
cosx
rfi
j
sinx
=
exp(kjx)
n+m
k=O
Properties
of
Logarithms
If logax
=
N,
then
aN
=
x
logax
=
logab logbx
log,ny
=
logun
+
log,y
log,x/y
=
logax
-
loguy

47-8
REFERENCE
DATA
FOR ENGINEERS
log,xY
=
y
log,x
log,b
=
l/logba
al%r
=
x
log,l
=
0
log,a
=
1
logex
=
1~
=
log,
10
loglox
=
2.30259
loglox
loglox
=
logloe logex
=
0.43429
logex
Sums
In this subsection, the following symbols will be
used:
T(a)
=
Gamma function of
a
n!
in which
n
and
k
are positive
integers,
n
2
k,
and
(nk)
=
k!(n
-
k)!
Arithmetic Progression:
n-1
k=O
2
(a
+
kd)
=a
+
(a
+
d)
+
(a
+
2d)
+
. .
.
+
[a
+
(n
-
1)dl
=
$n[2a
+
(n
-
I)~I
Geometric Progression:
n-1
k=O
ark
=
a
+
ar
+
ur2
+
*
* *
+
urn-'
=
[a@"
-
l)/(r
-
l)],
=
nu,
for
r
#
1
for
r
=
1
Sums
of
Powers
of
Integers:
2
k2
=
1'
+
2'
+
3'
+
* * *
+
n2
k=
I
.rt
1
-
--
+
inr
+
(2k)-I(
2k
I)L32k~r-2ktI
r+1
k=
I
where,
r
is a positive integer,
[r/2]
is the largest integer less than or equal to
r/2,
Bzk
is the 2kth Bernoulli number.
These
sums
are tabulated for
n
=
1,2,3,
*
for
r
=
1,
2, 3,
. .
-,
IO.*
obtained from the above. For example,
,
100
and
Sums
of integral powers of odd integers may be
2nt
1
k=
1
k=
1
=
k2
-
Z2
2
k2
Sums
of
Powers
of
Reciprocals
of
Integers:
m
&z)
=
(W)
=
(111')
+
(1/2')
+
(1/3')
+
.
.
.
k=
1
For Rez
>
1,
&z)
is
the Riemann zeta function of
z
00
(l/k2)
=
(111')
+
(1/2')
+
(1/3')
+
*
*
*
k=
1
=
7?/6
=
1.64493
m
(ilk3)
=
(1/i3)
+
(~2~)
+
(1133)
+
. . .
k=
1
=
1.20206
=
[n(n
+
1)(2n
+
1)/6]
(l/k2')
=
(1/l2')
+
(1/22')
+
(1/327)
+
. . .
k=
1
=
[n2(n
+
1)2/4]
=
f
n(n
+
1)(2n
+
1)(3n2
+
3n
-
1)
r
integral
Ir
Abrarnovitz,
M.
and Stegun,
I.
A.
Handbook
of
Mathe-
matical Functions.
Washington,
D.
C.:
National Bureau
of
Standards.

MATHEMATICAL EQUATIONS
47-9
where
BZr
is the
2rth
Bernoulli number. Values of
&z)
are tabulated for
z
=
2,
3,
4,
.
.
*
,
42,
to
20
decimal
truncated sums
(XI
+
x2
+
* *
+
x,)"
=
...
n!
x+
places in the
Handbook
of
Mathematical Functions.
The
n
n-nl
n-nl-q
n-n1-n2-'"-nr-2
r
nk
"1'0
n2=0
n3=0
nr-l=O k=l
nk.
2
(l/kr)
k=
1
are related to the polygamma functions.
Finite
Sums
of
Binomial Coeflcients:
i:
(
rn
;
")
=
(
;
)
+
(
rn
;
1)
+
. . .
k=O
=
(r
')
(r
2
n
and
s
2
n)
Binomial Theorem:
Nonnegative integral exponent:
(a
+
b)"
=
a"
+
na"-'b
+
i[n(n
-
l)]a"-2b2
For other
n,
integral negative and nonintegral, the
series will be infinite. For convergence it is assumed
la1
>
lbl.
(If
(a]
<
lbl,
interchange
a
and
b.)
Negative integral exponent:
0-n
-
na-n-1
b
(a
+
b)-"
+
f[n(n
+
l)]a-"-2b2
-
-
=
(-1)k(
+
-
l)a-n-kbk
k=O
k
Nonintegral exponent:
where the interpretation
n,
=
n
-
nl
-
n2
-
.
*
.
-
n,-l
is to be used in the final product.
Combinations and
Permutations
A
combination is a selection from a number of things
in which the order of the selected objects is disregarded,
whereas a permutation is a selection in which the order
is
taken into consideration. For example, if from the
letters
a,
b,
and
c
a group of two is selected, then
ab,
bc, ac
are the combinations and
nb, ba, bc, cb, nc, ca
are
the permutations.
The number of different combinations of
n
(dissimi-
lar) things taken
r
at a time is
The number of different permutations of
n
(dissimi-
lar) things taken
r
at a time is
Pf
=
n!/(n
-
r)!
=
n
X
(n
-
1)
X
-
X
(n
-
r
+
1)
Bernoulli Numbers
Definition:
B,
=
(d"/dx")[x/(ex
-
l)]lx=o
Values
for
Small
n:
B
-
1,B
-
-1
B
-I
0
-
1
-
2,
2-6,B4=
-&,
6
-
42,
8
-
30,
BIO
=
&*
B
-L
B
--I
B2n+l
=
0,
for all integral
n
>
0
Identities:
The latter identity may be used for recursive calculation
of the
B,'s.
Trigonometric Identities
1
=
sin2A
+
cos2A
=
sinA cscA
=
tanAcoL4
=
cosA secA
