Middleton W.M. (ed.) Reference Data for Engineers: Radio, Electronics, Computer and Communications
Подождите немного. Документ загружается.


47-10
REFERENCE
DATA
FOR ENGINEERS
sin4
=
cosA/cotA
=
llcscA
=
cod
tad
=
k(1
-
COS~A)”~
cosA
=
sinA/tanA
=
l/secA
=
sinAcotA
=
f(1
-
sin2A)”*
tad
=
sinA/cosA
=
llcotA
=
sin4 secA
sin4
=
(eJA
-
e-jA)/2j
cosA
=
(dA
+
e-jA)/2
sin(A
f
B)
=
sin4 COSB
+-
cosA sid
cos(A
k
B)
=
cosA COSB
7
sinA
sid
tan(A
f
B)
=
(tanA
t
tanB)l(l
F
tad tad)
=
(tad
COB
k
l)/(coB
T
tad)
cot(A
k
B)
=
(cotA
COB
7
l)/(coB
t
cotA)
=
(COtA
T
tad)/(l
f
COtA
tanB)
sin%
=
2sinA cosA
cos2A
=
cos2A
-
sin2A
tan2A
=
(2 tanA)/(l
-
tan2A)
sin3A
=
3 sinA
-
4 sin3A
cos3A
=
-3
COSA
+
4 cos3A
tan3A
=
(3 tanA
-
tan3A)/(l
-
3 tan2A)
cosnA
=
Re(cosA
+
j
sinA)”
sinnA
=
Im(cosA
+
j
sinA)”
siniA
=
f
[(l
-
cosA)/2]
’”
cosiA
=
+[(1
+
c0sA)/2]”~
taniA
=
sinA/(l
+
cowl)
=
(1
-
cosA)/sinA
sin4
f
sid
=
2 sini(A
f
B)
cosi(A
T
B)
COSA
+
COSB
=
2 COS~(A
+
B)
COS$(A
-
B)
COSB
-
cod
=
2
sini(A
+
B)
&$(A
-
B)
tanA
f
tad
=
[sin(A
-I
B)/cosA cosB]
cotA
f
cos
=
[sin(B
f
A)lsinA sinB]
sin2A
-
sin2B
=
sin(A
+
B)
sin(A
-
B)
cos2A
-
sin2B
=
cos(A
+
B)
cos(A
-
B)
tan$(A
k
B)
=
(sinA
f
sid)/(cosA
+
COSB)
CO~+(A
T
B)
=
(si&
*
sid)/(cosB
-
cod)
cos2A
=
i(cos2A
+
1)
cos3A
=
3cos3A
+
3 cosA)
cos4A
=
i(cos4A
+
4 cos2A
+
3)
sin2A
=
i(-cos%
+
1)
sin3A
=
f(-sin3A
+
3
sinA)
sin4A
=
i(cos4A
-
4 cos2A
+
3)
sinA COSB
=
$[sin(A
+
B)
+
sin(A
-
B)]
COSA
COSB
=
~[cos(A
+
B)
+
COS(A
-
B)]
sinA sinB
=
f[cos(A
-
B)
-
COS(A
+
B)]
sinA
+
msinB
=
psinC
with
p2
=
1
+
m2
+
2m cos@
-
A)
and
tan(C
-
A)
=
[msin(B
-
A)]/[l
+
m
cos(B
-
A)]
2
Aiexp(jei)
=
pej$
i
with
In the previous notation
2
A~
sinei
=
p
sin+
i
apply
*
sinx
+
sin2x
+
sin3x
+
. . .
+
sinmx
=
[sin+sini(m
+
l)x/sinix]
cosn
+
cos2x
+
cos3x
+
.
.
.
+
cosmx
=
[sin$mxcos&n
+
l)x/sinixl
MATHEMATICAL EQUATIONS
47-1
1
sinx
+
sin3x
+
sin5x
+
.
*
+
sin(2m
-
1)x
=
(sin2m/sinx)
cosx
+
cos3x
+
cos5x
+
*
*
.
+
cos(2m
-
1)x
=
(sin2ml2 sinx)
f
+
cosx
+
cos2x
+
*
.
* +
cosm
=
[sin(m
+
$x12
sinixl
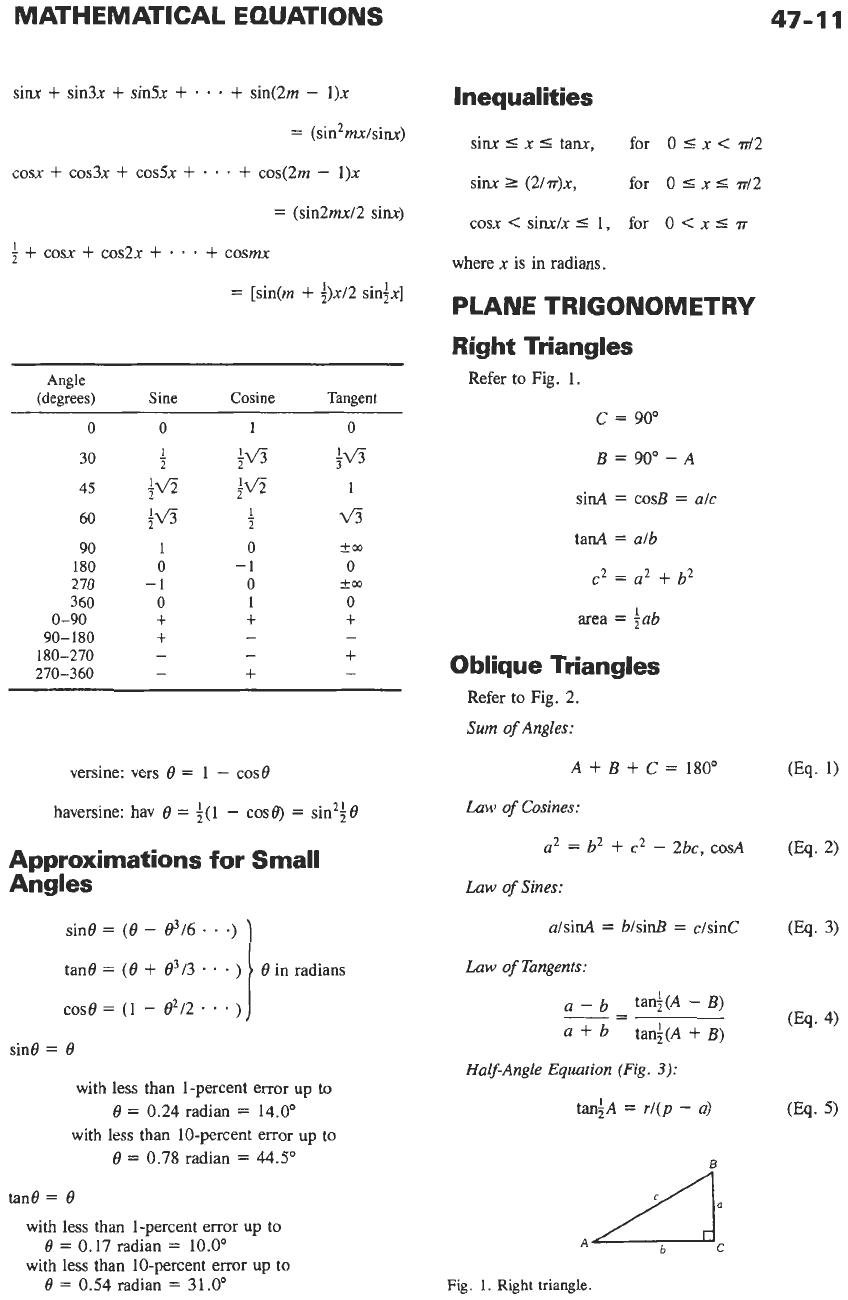
Angle
(degrees)
Sine
Cosine
Tangent
0
0
1
0
1
-
30
2
fv3
$5
45
;v3
fv3
1
60
fV?
2
v3
90
1
0
-+m
180
0
-1
0
270
-1
0
+.m
360
0
1
0
0-90
+
+
+
+
1
- -
90-180
+
180-270
- -
+
270-360
- -
versine: vers
0
=
1
-
cos0
haversine: hav
9
=
f(1
-
cos@
=
sin2i9
Approximations for Small
Angles
tan9
=
(0
+
03/3
.
3
.
)
sin0
=
(0
-
g3/6
. .
e)
cos9
=
(1
-
02/2.
* *
)
sin9
=
0
with less than 1-percent error up to
0
=
0.24 radian
=
14.0"
with less than 10-percent error up to
0
=
0.78 radian
=
44.5"
tan0
=
0
with less than 1-percent error
up
to
with less than 10-percent error up to
0
=
0.17 radian
=
10.0"
0
=
0.54 radian
=
31.0"
Inequalities
sinx
5
x
5
tanx,
for
0
5
x
<
d2
sinx
2
(2/~)x, for
0
5
x
I
~12
cosx
<
sinxlx
5
1,
for
0
<
x
I
T
where
x
is in radians.
PLANE TRIGONOMETRY
Right Triangles
Refer to Fig. 1.
c
=
90"
B
=
90"
-
A
sin4
=
cosB
=
alc
tanA
=
alb
c2
=
a'
+
b2
area
=
fab
Oblique Triangles
Refer to Fig. 2.
Sum
of
Angles:
A
+
B
+
C
=
180"
0%.
1)
Law
of
Cosines:
U'
=
b2
+
c2
-
2bc,
COSA
(Eq.
2)
Law
of
Sines:
alsinA
=
bIsinB
=
c1sinC
(Eq.
3)
Law
of
Tangents:
a
-
b
tani(A
-
B)
(Eq.
4)
-=
a
+
b
tani(A
+
B)
Half-Angle
Equation
(Fig.
3):
tanfA
=
r/(p
-
a)
A
b
C
Fig.
1.
Right triangle.

47-12
REFERENCE DATA FOR ENGINEERS
C
b
A
Fig.
2.
Oblique triangle.
where,
Solving an Oblique Triangle:
Given
Use
Eq.
To
Obtain
aBC
(1)
A
(3)
bc
Abc
(1)
B
+
C
hence
(4)
B
-
C
B,C
abc
(5)
or
(2)
ABC
abA
ambiguous
(3)
and
(1)
BCc
case
SPHERICAL TRIGONOMETRY
Spherical triangles are bounded by the arcs of great
circles. These are circles formed by the intersection
of
a
sphere with planes passing through the center of the
sphere.
In
the following equations,
a,
p,
y
are
the
angles, and a,
b,
c
are the corresponding opposite sides,
respectively. The sides are measured by the angles
subtended by the arcs; for example, a side extending
from the Equator to the North Pole is a 90” side.
Right Spherical Triangles
(Y
=
907
Refer to Fig.
4.
cosc
=
cosa cosb
=
cota cotp
cosa
=
sinP cosa
=
tanb cotc
cosp
=
sina cosb
=
tana cotc
P
db
A
A
k-P-4
C
Fig.
3.
Half angle.
sina
=
sinc sina
=
tanb cotp
sinb
=
sinc
sinp
=
tana cota
(Eq.
6)
Oblique Triangles
Refer to Fig.
5.
Law
of
Cosines
for Sides:
cosa
=
cosb cosc
+
sinb sinc cosa
cosb
=
cosc cosa
+
sinc sina cosp
cosc
=
cosa cosb
+
sina sinb cosy
(Eq.
7a)
Law
of
Cosines
for
Angles:
cosa
=
-cosp cosy
+
sinp siny cosa
cosp
=
-cosy cosa
+
siny sina cosb
cosy
=
-cosa cosp
+
sina sinp cosc
Law
of
Sines:
(Eq.
7b)
sinalsina
=
sinblsinp
=
sinclsiny
(Eq.
8)
Napier’s Analogies:
P
c&
Y
a
Fig.
4.
Right spherical triangle.
Fig.
5.
Oblique spherical triangle.

MATHEMATICAL EQUATIONS
47-13
Half-Angle Equations:
tania
=
tanr/sin(p
-
a)
tan;@
=
tanr/sin(p
-
b)
taniy
=
tanr/sin(p
-
c)
(Eq.
loa)
where 2p
=
a
+
b
+
c
and
sin(p
-
a)
sin@
-
b) sin(p
-
c)
sinp
tan’r
=
sin’
:a
=
[sin@
-
b)
sin(p
-
c)/sinb sinc]
cos’
+a
=
[sinp sin(p
-
a)/sinb sinc]
tan’
fa
=
[sin@
-
b) sin(p
-
c)/sinp sin(p
-
a)]
(Eq.
lob)
and equations obtained by cyclical permutation for
p
and
y.
Half-Side Equations:
tanfa
=
tad sin(a
-
E)
tanib
=
tad sin@
-
E)
tanic
=
tad sin(y
-
E)
(Eq.
lla)
where 2E
=
a
+
/3
+
y
-
T
is the spherical excess and
sinE
sin(a
-
E)
sin@
-
E)
sin(y
-
E)
tan’R
=
sin’
;a
=
-[sinE sin(E
-
a)/sinp shy]
cos’
&a
=
[sin(E
-
p)
sin@
-
y)/sinp siny]
tan’
;a
=
-[si& sin(E
-
a)/sin(E
-
p)
sin(E
-
y)]
(Eq.
llb)
and equations obtained by cyclical permutation for b
and
c.
Area: On a sphere
of
radius one, the area of a triangle
is equal to the spherical excess
2E=
a
+
/3
+
-
T
L’Huilier’s Theorem:
tan2
;E
=
tan$ tan+(p
-
a)
X
tan;@
-
b) tan;(p
-
c)
(Eq.
12)
Solving
an
Oblique Triangle*:
*
See
also great-circle calculations in Chapter
33.
Use
Given Eq
.
To
Obtain
abc
aPY
.pc
aba
ambiguous
ab
ambiguous
case
case
aPY
abc
a
rt
P,
hence
a#,
then
c
a
f
6,
hence
a,b,
then
y
CY
b
CY
P
HYPERBOLIC FUNCTIONS*
sinhx
=
(e”
-
e-”)/2
coshx
=
(e”
+
e-”)/2
tanhx
=
sinhx/coshx
=
[l
-
exp(-2x)]/[l
+
exp(-2x)]
=
lkothx
sechx
=
l/coshx
cschx
=
llsinhx
sinh(-x)
=
-sink
cosh(-x)
=
COS^
tanh(-x)
=
-tank
coth(-x)
=
-cothx
sinhjx
=
j
sinx
coshjx
=
cosx
tanhjx
=
j
tanx
cothjx
=
-j
cotx
cosh’x
-
sinh’x
=
1
1
-
tanh2x
=
licosh’x
coth2x
-
1
=
l/sinh2x
sinh2x
=
2 sinhx coshx
cosh2x
=
cosh’x
+
sinh’x
sinh(x
4
jy)
=
sinhx cosy
f
j
coshx siny
cosh(x
C
jy)
=
coshx cosy
f
j
sink siny
*
Tables
of
hyperbolic functions appear in Chapter
48.

47-14
REFERENCE
DATA
FOR ENGINEERS
tanh(x
*
y)
=
(tanhx
2
tanhy)/(l
2
tanhx tanhy)
If y
=
gdx (guderrnannian of
x)
is defined by
x
=
log, tan(fa
+
4y)
then
sinhx
=
tany
coshx
=
secy
tanhx
=
siny
tanh(x/2)
=
tan(
y/2)
HYPERBOLIC TRIGONOMETRY
Hyperbolic (or pseudospherical) trigonometry ap-
plies to triangles drawn in the hyperbolic type of
non-Euclidean space. Reflection charts, used in trans-
mission-line theory and waveguide analysis, are models
of this hyperbolic space.*
Conformal Model
The space is limited to the inside of a unit circle,
I?.
Geodesics (or “straight lines” for the model) are arcs
of circle orthogonal to
r
as shown in Fig.
6.
The
hyperbolic distance between two points
A
and
B
is
defined by
[AB]
=
log,[(BI/BJ):(AI/AJ)]
where
I
and
J
are the intersections with
r
of geodesic
AB. The distance [AB] is expressed in nepers. For
engineering purposes, a unit corresponding to the
decibel and equal to
U8.686
neper is sometimes used.
As this model is conformal, the angle between two
lines is the ordinary angle between the tangents at their
common point.
*
G.
A.
Deschamps,
Hyperbolic Protractor for Microwave
Impedance Measurements and Other Purposes.
New
York:
International Telephone and Telegraph Corp.,
1953.
J
Projective Model
The space is again composed of the points inside a
circle,
I?.
Geodesics
are
straight-line segments limited
to the inside of
r
(JI
in Fig.
7).
The hyperbolic distance AB is defined by
<AB>
=
ilog,[(BI/BJ):(AI/AJ)]
and can be measured directly by means of a hyperbolic
protractor. The angles for this model do not appear in
true size except when at the center of
r.
An angle such
as BAC, when it is considered in reference to the
projective model, will be called an
elliptic
angle. It can
be evaluated, as shown in Fig.
8,
by projecting B and
C
through the hyperbolic midpoint of OA onto
B
’
and
C
’
on circle
r,
then measuring
B’OC‘
as in Euclidean
geometry.
The two models in Fig.
9
drawn inside the same
circle
l7
can be set into a distance-preserving correspon-
dence by the transformation:
%(M)
=
M’
defined by
[OM]
=
<OM’>
or in terms of ordinary distances
OM’
=
20M/(1
+
OM2)
The hyperbolic distance to the center
0
being denoted
by
OM
=
tanh(u/2)
and
OM’
=
tanhu
The points on
r
are at an infinite distance from any
point inside
r.
In the following equations, the sides
are
expressed in
nepers, the angles in radians. The three points
A,B,C
are assumed to be inside circle
r.
Fig.
6.
Conformal model.
Fig.
7.
Projective model.

MATHEMATICAL EQUATIONS
47-15
Fig.
9.
Correspondence between the two models.
Fig.
8.
Construction
of
angle on projective model.
or
Right Hyperbolic Triangles
(y
=
90q
Refer to Figs. 10 and
1
1.
coshc
=
cosha coshb
=
cota cotp
cosa
=
sinp cosha
=
tanhb cothc
cosp
=
sina coshb
=
tanha cothc
When
B
is at infinity,
i.e.,
on
r
cosA
=
tanhb
cotA
=
sinhb
cscA
=
coshb
tan$
=
expb
(712)
-
A
=
gdb
(See definition of gd in section “Hyperbolic Func-
tions.”)
CB
and
AB
are “parallel.”
A
is also called angle
of
parallelism and is noted by
A
=
n(b)
=
~12
-
gdb
Oblique Hyperbolic Triangles
Law
of
Cosines:
cosha
=
coshb coshc
-
sinhb sinhc cosa
and permutations
(Eq.
13a)
cosa
=
-cosp cosy
+
sinp sin
y
cosha
and permutations
(Eq.
13b)
Law
of
Sines
(Fig. 12):
sinhalsina
=
sinhbisinp
=
sinhclsiny
(Eq.
14)
B
Fig.
11.
Conformal representation
of
right hyperbolic trian-
gle with
B
at infinity. Fig.
10.
Projective representation
of
right hyperbolic triangle.

47-16
REFERENCE
DATA
FOR ENGINEERS
Fig.
12.
Oblique hyperbolic triangle.
Napier’s Analogies:
sini(a
-
p)
sini(a
+
p)
tanhic
cosi(a
-
p)
cosi(a
+
p)
tanhic
sinhi(a
-
b)
tanhg(a
-
b)
- -
(Eq. 15a)
tan+(a
+
b)
-
-
(Eq. 15b)
tani(a
-
p)
- -
(Eq. 15c)
sinh;(a
+
b)
cot;
y
coshi(a
+
b) cot;
y
coshi(a
-
b)
tani(a
+
p)
-
-
(Eq. 15d)
Half-Angle Equations:
tania
=
tanhr/sinh(p
-
a)
and permutations where 2p
=
a
+
b
+
c
and
sinh(p
-
a) sinh(p
-
b) sinh(p
-
c)
sinhp
tanh’r
=
(Eq. 16a)
sinh(p
-
b) sinh(p
-
c)
sinhb sinhc
sin2
+a
=
sinhp sinh(p
-
a)
sinhb sinhc
cos2
iff
=
(Eq. 16b)
sinh(p
-
b) sinh(p
-
c)
sinhp sin(p
-
a)
tan’
;a
=
Half-Side
Equations:
cothia
=
cothR/sin(A
+
a)
and permutations where 2A
=
7
-
a
-
p
-
y
is the
hyperbolic defect and
sinA
sin(A
+
a)
sin(A
+
p)
sin(A
+
y)
tanh2R
=
(Eq. 17a)
-
sin(A
+
p)
sin(A
+
7)
cosh
*a
-
sinp siny
(Eq. 17b)
sinA sin(A
+
a)
sin(A
+
p)
sin(A
+
y)
tanh’ia
=
.
Area: The hyperbolic area of a triangle is equal to the
hyperbolic defect.
28
=
-
(a
+
p
+
7)
(Eq.
18)
Solving an Oblique Hyperbolic Triangle: Solution of
an oblique hyperbolic triangle is analogous to that for
an oblique spherical triangle, as follows.
Given
Use
Eq.
To
Obtain
abc
ffPY
ab
ffpc
aba
ambiguous
a@
ambiguous
case
case
ffPY
abc
a
Ifr
p,
hence
a,
p.
a
f
b,
hence
a, b,
P
then
c
then
y
CY
b
CY
PLANE ANALYTIC GEOMETRY
In the following,
n
and y are coordinates of a variable
point in a rectangular-coordinate system.
Straight
Line
General Equation:
Ax+By+C=O
A,
B,
and
C
are constants.
Slope-Intercept
Form
(Fig.
13):
y=sx+b
b
=
y-intercept
Y
I
sinh
2a
-
-
sinA sin(A
+
a)
sinp siny
Fig.
13.
Slope-intercept.

MATHEMATICAL EQUATIONS
Y
47-17
Y
Fig.
14.
Intercept-intercept.
Fig.
15.
Point-slope,
s
=
tme
=
slope
Intercept-Intercept Form (Fig.
14):
(xla)
+
(y/b)
=
1
a
=
x-intercept
b
=
y-intercept
Point-Slope Form (Fig.
15):
y
-
y1
=
s(x
-
XI)
A B
distance
=
*(A2
+
B
2
)
112”
+
-+(A2
+
B
2
)
IiZYl
C
?(A2
+
B2)Ii2
+
Angle Between Two Lines:
tan+
=
(s,
-
s2)/(1
+
sIs2)
where,
r#~
=
angle between the lines,
s1
=
slope
of
one line,
s2
=
slope
of
other line.
When the lines are mutually perpendicular, tan+
=
km,
whence
s,
=
-us2
s
=
tan0
Transformation of Rectangular
Coordinates
(xl
,
y,)
=
coordinates of known point
on
line.
Translation:
Point-Point Form:
where (x,, y,) and (x2, y2)
are
coordinates
of
two
Y1
=k+Yz
x2
=
XI
-
h
Y2
=
YI
-
k
different points
on
the line.
Normal Form:
A B
+(A2
+
B2)1/Zx
+
?(A2
+
B2)112y
(h,
k)
=
coordinates of new origin
referred to old origin
C
+(A2
+
g2)1/2
=
Rotation (Fig.
16):
+
The sign of the radical is chosen
so
that
X,
=
x2
cos0
-
y2 sin0
<o
+(A2
+
B2)1‘2
Distance From Point
(x,,
yl)
to
a
Line:
Substitute
coordinates
of
the point in the normal form
of
the line.
Thus
y1
=
x2
sin0
+
y2 cos0
x2
=
x1 cos0
+
y1 sin0
y2
=
-xl
sin0
+
yI cos0
(x,,
yI)
=
“old” coordinates

47-18
REFERENCE
DATA
FOR ENGINEERS
Fig.
16.
Rotation
of
axes.
(x2,
y2)
=
“new” coordinates
t9
=
counterclockwise angle of
rotation of axes
Circle
The equation of a circle of radius
r
with center at
(m,
n)
is
(x
-
rn)’
+
(y
-
n)’
=
r2
Tangent Line to a Circle:
At
(xi,
yl)
is
Y
-
y1
=
-[(XI
-
m)/(yl
-
n)l(x
-
XI)
Normal Line to a Circle:
At
(XI,
yi)
is
y
-
Y1
=
[(Yi
-
nMXl
-
m)l(x
-
XI)
Para
bola
Fig.
17
shows an x-parabola centered at the origin
open to the right.
Focus:
F
Directrix:
D
Vertex:
0
Latus rectum:
AA
‘
e
=
eccentricity
=
1
MP/FP
=
1
for any point
P
on the parabola
x-Parabola:
(y
-
k)2
=
*2p(x
-
h)
where
(h,
k)
are the coordinates of the vertex, and the
sign used is plus or minus when the parabola is open to
the right or to the left, respectively. The semilatus
rectum is
p.
y-Parabola:
(x
-
h)2
=
*2p(y
-
k)
where
(h,
k)
are
the coordinates of the vertex. Use plus
sign if parabola is open above, and minus sign if open
below.
Fig.
17.
Parabola.
Tangent Lines to a Parabola:
(xi,
yl)
=
point of tangency
For x-parabola
Y
-
Y1
=
k[P/(Yl
-
k)l(x
-
XI)
Use plus sign if parabola is open to the right, minus sign
if open to the left.
For y-parabola
Y
-
Y1
=
*[(XI
-
hYPl(X
-
Xl)
Use plus sign if parabola is open above, minus sign if
open below.
Normal Lines
to
a Parabola:
(x,
,
y
=
point of contact
For x-parabola
Y
-
YI
=
3KYl
-
kYPl(X
-
XI)
Use minus sign if parabola
is
open to the right, plus sign
if open
to
the left.
For y-parabola
Y
-
Yl
=
-
h)l(x
-
XI)
Use minus sign if parabola is open above, plus sign if
open below.
Ellipse
Fig.
18
shows an ellipse centered at the origin. If the
ellipse is centered at
(h,
k)
instead, the equations that
follow must be modified by replacing
x,
xl,
y,
yl
by
x
-
h,
xl
-
h,
y
-
k,
yI
-
k,
respectively.
Foci:
F, F’
Directrices: D. D‘
e
=
eccentricity
<
1

MATHEMATICAL EQUATIONS
47-19
C,iwx
B’
Fig.
18.
Ellipse.
2a
=
A’A
=
major axis
2b
=
BB’
=
minor axis
2c
=
FF’
=
focal distance
Then
OC
=
ale
BF
=
a
FC
=
ae
1
-
e2
=
b2/az
Equation
of
Ellipse:
(x2/a2)
+
(y2/b2)
=
1
Sum
of
the Focal Radii:
To any point on ellipse
=
2a
Equation
of
Tangent Line
to
Ellipse:
(xI,
yl)
=
point of tangency
(xxI/a2)
+
(yyl/b2)
=
1
Equation
of
Normal Line
to
an Ellipse:
Y
-
Y
1
=
(a2Y
1
lb2X1
)(x
-
XI)
Hyperbola
Fig.
19
shows an x-hyperbola centered at the origin.
If
the hyperbola is centered at
(h,
k)
instead, the
equations that follow must be modified by replacing
x,
xl,
y,
y1
byx
-
h,
xl
-
h,
y
-
k,
yl
-
k,
respectively.
Foci:
F,
F’
Directrices:
D,
D’
e
=
eccentricity
>
I
2a
=
transverse axis
=
A’A
Fig.
19.
Hyperbola.
CO
=
de
CF
=
ae
Equation
of
x-Hyperbola:
(x2/a2)
-
(y2/b2)
=
1
where,
b2
=
a2(e2
-
1)
Equation
of
Conjugate
(
y-) Hyperbola:
(y2/b2)
-
(x2/a2)
=
1
Tangent Line to x-Hyperbola:
(xl,
yl)
=
point of tangency
a2yly
-
b2xln
=
-a2b2
Normal Line to x-Hyperbola:
y
-
y,
=
-(a2yl/b2x1)(x
-
xl)
Asymptotes to Hyperbola:
y
=
?(b/a)x
SOLID
ANALYTIC GEOMETRY
In the following,
x,
y,
and
z
are
the coordinates of a
variable point in space in a right-handed rectangular-
coordinate system. See Fig.
20.
Coordinates
(no,
Yo,
zo).
Direction Cosines
and Numbers
The coordinates of a point are given by a triplet, e.g.,
In
Fig.
20,
a,
/3,
and yare the angles line
OP
makes
with the
x,
y,
and
z
axes, respectively.
Coscl,
cos& and
cosy are the direction cosines of line
OP.
Numbers
