Middleton W.M. (ed.) Reference Data for Engineers: Radio, Electronics, Computer and Communications
Подождите немного. Документ загружается.


47-40
REFERENCE
DATA
FOR ENGINEERS
Asymptotic Expansions:
21
4!
6!
sinz
ci(z)
-
(1
-
,Z
+
7
-
7
+
*
9
*
Gamma Function
Definition:
r(z)
=
1;
tz-'e-'dt
T(-z)
=
-T/[r(z
+
1)
sin~z], Rez
>
0
The function r(z) is an analytic function everywhere
except at the negative integers.
Identities:
Special Values:
Special Values:
+(")(I)
=
(-l)ntln!&
+
11,
n
=
I,
2,
*
.
*
$tu
=
-Y
+(n)($
=
(-1)~+'n!(2~+'
-
1)l(n
+
11,
n=l,2;.*
=
-y
-
2
1n2
in which
C(n
+
1) is the Riemann zeta function of
n
+
1.
Series Expansions:
m
$t1
+
z)
=
-y
-
2
(-l)kL(k
+
l)zk,
/zI
<
1
k=
1
Asymptotic Expansions:
+(")(z)
-
[(-l)"(n
-
l)!/zn][I
+
(n/2z)
+
* *
-1,
as z+m, (argzl
<
T,
n
=
1,2,
.
$tz)
-
lnz
-
(1/2z)
+
.
.
'
6
7
8
9
10
T(n)
=
(n
-
l)! 1
1
2
6
24 120 720
5040
40
320 362
880
Asymptotic Expansion (Stirling's Equation):
r(z)
-
e-zzz-1'2(2~)'~2[1
+
(11122)
+
(1/288z2)
+
.I
Note z!
=
zT(z)
-
e~2z2t1'2(2~)"2[1
+
(11122)
+
(1/288z2)
+
.
.
.I
Psi and Polygamma Functions
Error
Function
Definitions: Dejinitions:
+(O)(z)
=
Nz) is known as the psi function, and
+(n)(z) as the polygamma function of
order
n,
n
=
1,
2,
.
.
erfz
=
(2/d2)
exp(-t2)dt
=
1
-
erfz

MATHEMATICAL EQUATIONS
47-41
The path
of
integration for large
t
must remain within
largtl
<
d4
in the latter integral.
Derivatives:
(d("+')
/dzcfl+ '))erfz
=
(-1)"(2/rr"2)~,(z)e-'2,
n
0,
I,
2,
. .
*
where
H,(z)
is the Hermite polynomial of order
n.
Relation
to
Gaussian Distribution:
Fresnel Integrals
Dejinitions:
C(z)
=
16'
cos[(7~/2)t~ldt
Series Expansions:
Asymptotic Expansions:
1'3
1'3.5.7
-
. .
.)-
sin;
m2
(7772)4
57-2
1.3-5.7.9
cos;
m2
+
(vz~)~
1.3.5.7.9
+
(d5
Elliptic Integrals
First Kind:
Second Kind:
E(@,
k)
=
I,"
(1
-
k2
sir~~B)"~dB
If
C#J
=
7d2,
the elliptic integrals are said to be
complete, and they are denoted by
K
or
K(k)
and
E
or
W).
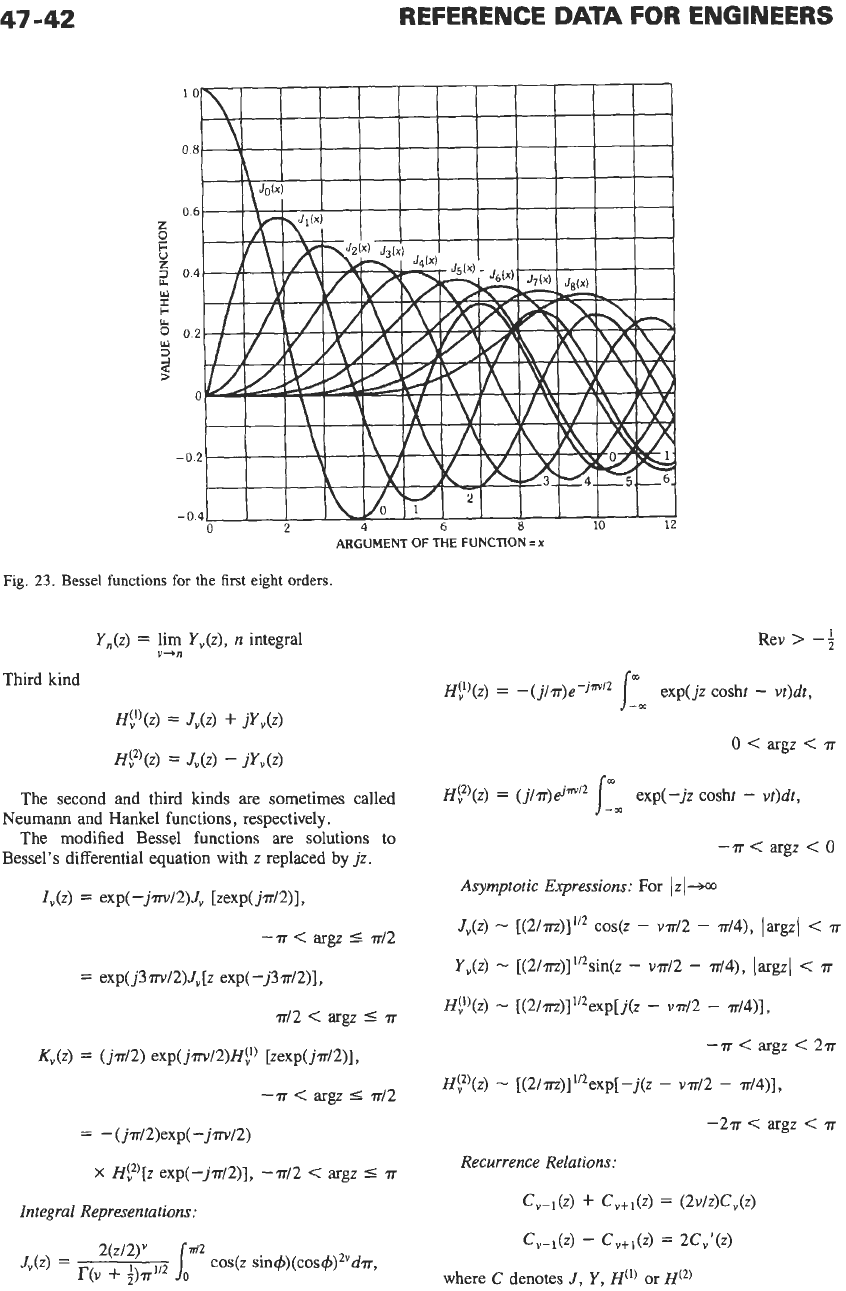
Bessel Functions*
Refer to
Fig.
23.
Dejinitions:
Bessel functions are solutions to Bessel's
differential equation
z2(d2w/dz2)
+
z(dw/dz)
+
(2'
-
v2)w
=
0
They are divided into
First kind
Second kind
J"(2)
cosv7r
-
J-,(Z)
Y,(Z)
=
sinnv
,
v
not
an
integer
*
For
an
extensive treatment
of
Bessel
functions,
see
G.
N.
Watson,
A
Treatise
on
the
Theory
of
Bessel
Functions, New
York:
Cambridge University Press,
1943.
24fl+3,
JzI
<
00
(-l)"(.rr/2)2"fl
'(')
=
zo
(2n
+
1)!(4n
+
3)
47-42
REFERENCE
DATA
FOR
ENGINEERS
ARGUMENT
OF
THE FUNCTION
=
x
Fig. 23. Bessel
functions
for
the
first
eight orders.
Y,(z)
=
lim
Y,(z),
n
integral
v+n
Third kind
H‘,”(z)
=
JJZ)
+
jY,(z)
H$Z)(z)
=
J,(z)
-
jY,(z)
The second and third kinds
are
sometimes called
The
modified Bessel functions are solutions
to
Neumann and Hankel functions, respectively.
Bessel’s differential equation with
z
replaced by
jz.
I&)
=
exp(-jm/2)Jv [zexp(j?r/2)],
-T
<
argz
5
d2
=
exp(j3m/2)JV[z exp( -j37~/2)],

MATHEMATICAL EQUATIONS
47-43
Series Containing Bessel Functions:
exp(-ju situ)
=
2
JJU)
exp
(-jnx)
X
n=-m
m
cos@
cosx)
=
J&)
+
22
(-l)nJ&)
cos2nx
n=l
X
cos(2n
-
l)x
Orthogonal Polynomials
Any set of polynomials
cf,(x)}
with the property
6
w(x)~(x)f~(x)d~
=
0,
for
rn
z
n
=
h,, for
rn
=
n
is called a set of orthogonal polynomials on the interval
(a,
b)
with respect to the weight function
w(x).
These
functions occur in the Gauss quadrature equations
among other places. Chebishev polynomials are in-
volved in the theory of the Chebishev filter; Hermite
polynomials arise in the refinements
of
the central limit
theorem, the so-called Edgeworth series, etc. The
important properties are summarized in Table
1.
NUMERICAL ANALYSIS
Algorithms for Solving
F(x)
=
0
Bisection Method and Regula
Falsi
(Rule
of
False
Position): First determine
x,
and
x2
such that
F(x1)F(x2)
<
0,
Le.,
xl
and
x2
are points at which the
function has opposite signs.
Bisection Method: Calculate
x3
=
(x,
+
x,)/2
Regula Falsi: Calculate
To obtain the next approximation, take
x3
and
xi,
i
=
1
or
2,
such that
F(x3)F(xi)
<
0,
and repeat the
procedure.
Newton-Raphson: Take some initial value
xl
and
calculate successively
xn+l
=
xn
-
[F(x,)/F'(x,)],
n
=
1,
2,
3
*
.
This method may not converge. When it converges,
the rate
of
convergence is generally faster than the
bisection method or the regula falsi.
Algorithm for Solving
Fk
Y)
=
G(x,
Y)
=
0
The following is an extension of the Newton-
Raphson method described above. Take some initial
values
xI
and
yl
and calculate successively
TABLE
1.
PROPERTIES
OF
ORTHOGONAL POLYNOMIALS
e
-9
H,(x)
Hermite
--co
t,(x)
Laguerre
0
-co
e
-'
P,,(x)
Legendre
-
1
1
I
1
*
[n/2]
denotes
the
largest integer
less
than
or
equal
to
n/2.

47-44
REFERENCE DATA
FOR
ENGINEERS
x,+~
=
x,
+
[
(gG
-
F5)
/
dY
for
n
=
1,
2,
3,
.
*
-
.
By using Taylor’s series to first derivatives and
Cramer’s rule, this algorithm may be further extended
to the case of
rn
simultaneous equations in
rn
variables.
Interpolation Polynomial
The polynomial of lowest degree that passes through
n
points
(xi,
yi),
i
=
1,
2,
.
*
.
,
n,
is given by
where
xi
#
xk
for
i
f
k.
Interpolation at Equidistant
Points
Let
x
=
f(X0
+
ih)
g,
=
g(x
+
ik
Y
+
$1
Then
f(xo
+
ph)
may
be
approximated by
(1
-
p)fo
+
pfl,
given two points
IP(P
-
w2lf-I
+
(1
-
P2%
+
[P(P
+
WlA7
given three points
[-p(P
-
l)(P
-
2)/6If-l
+
t(P2
-
l)(P
-
2Y21.6
+
+
2)/21fl
+
MP2
-
1)/61f2,
given four points
g(xo
+
ph,
yo
+
qk)
may be approximated by
(1
-
p
-
q)gm
+
pgl0
+
qgol,
given three points
(1
-
P)(l
-
4)gm
+
P(1
-
dg10
+
4(1
-
Plgo,
+
P4811.
given four points
Integration
Refer to Fig. 24. Let
Ji’
=
f(xo
+
ih)
(Trapezoidal Rule)
t
2fZn-2
+
4f2n-1
+fin>
(Simpson’s Rule)
Differentiation
If
a functionf(x)
is
known at two points
a
and
b,
then
f’(4
=
tf@)
-
f(a)l/(b
-
a)
If
f(x)
is given at a discrete set of points, one may
differentiate the interpolation polynomial stated above.
The equation simplifies when the derivative
is
calculat-
ed at interpolation points that are equidistant,
for
example
f-1’
2
(1/2h)(-3f-l
+
4fo
-
fi)
fo’
=
(w4(-f-l
+fi)
fi’
=
(1/W(f-I
-
4fo
-b
3fi)
where,
Ji’
=f(x,
+
ih),
i
=
-1,
0,
1
Error
in
Arithmetic Operations
Let the quantities
A
and
B
be known to within errors
of
a
and
b,
respectively, where
a
and
b
are small relative
to
A
and
B.
Then
xm-1
For
Simpson’s
rule,
m
must
be
even.
Fig.
24.
Integration.

MATHEMATICAL EQUATIONS
Maximum
Error
(to
first order in
a
and
b)
Operation
The magnitude,
q,
of
small random errors often has a
normal distribution
47-45
Letf(x,
,
x2,
.
*
,
x,)
be a function
of
n
variables
xi,
which have normally distributed independent errors
qi
with indices
of
precision
hi.
Then
f(x,,
x2,
-
* *
,
x,)
will have an error
Q,
which is also normally distributed
with index
of
precision
H.
For small errors
H
=
{[hl-’(af/aql)]*
+
[h*-l(aflaq2)12
+
’
‘
+
[h,
-
’
(af/aqn)]2}
-
where
h
is called the index
of
precision. The rms of
q,
denoted by
u,
is, in terms of
h

48
Mathematical Tables
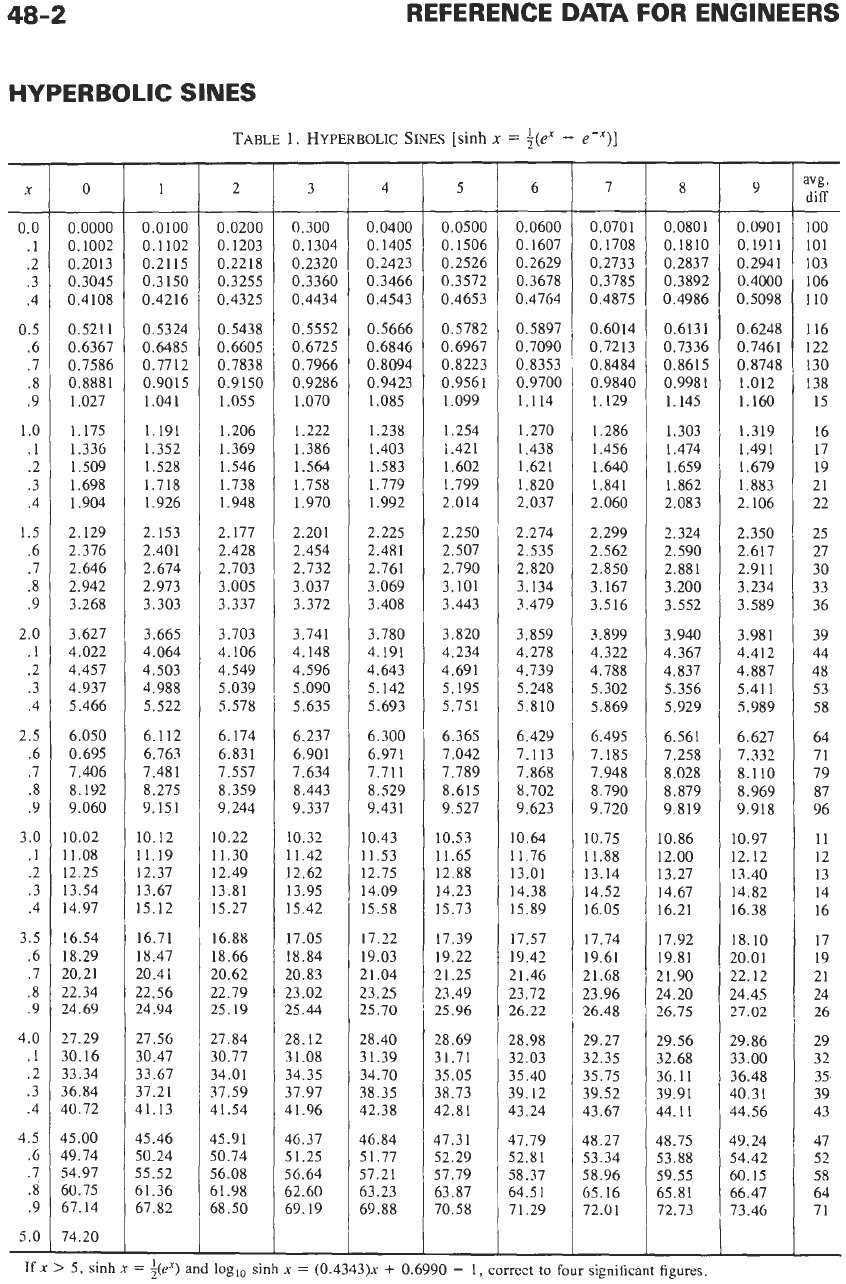
Hyperbolic Sines
48-2
Hyperbolic Cosines
48-3
Hyperbolic Tangents
48-4
Multiples
of
0.4343
48-4
Multiples
of
2.3026
48-5
Logarithms to Base 2 and Powers
of
2
Random Digits
48-6
Exponentials
48-7
Normal or Gaussian Distribution
48-8
Bessel Functions
48-9
48-5
48-
1
48-2
HYPERBOLIC
SINES
7
0.0701
0.1708
0.2733
0.3785
0.4875
0.6014
0.7213
0.8484
0.9840
1.129
1.286
1.456
1.640
1.841
2.060
2.299
2.562
2.850
3.167
3.516
3.899
4.322
4.788
5.302
5.869
6.495
7.185
7.948
8.790
9.720
-
X
E
0.0801
0.1810
0.2837
0.3892
0.4986
0.6131
0.7336
0.8615
0.9981
1.145
1.303
1.474
1.659
1.862
2.083
2.324
2.590
2.881
3.200
3.552
3.940
4.367
4.837
5.356
5.929
6.561
7.258
8.028
8.879
9.819
0.0
.1
.2
.3
.4
0.5
.6
.7
.8
.9
1
.o
.1
.2
.3
.4
1.5
.6
.7
.8
.9
2.0
.1
.2
.3
.4
2.5
.6
.7
.8
.9
3
.O
.1
.2
.3
.4
3.5
.6
.7
.8
.9
4.0
.1
.2
.3
.4
4.5
.6
.7
.8
.9
5.0
17.74
19.61
21.68
23.96
26.48
29.27
32.35
35.75
39.52
43.67
0
17.92
19.81
21.90
24.20
26.75
29.56
32.68
36.11
39.91
44.11
0.0000
0.1002
0.2013
0.3045
0.4108
0.5211
0.6367
0.7586
0.8881
1.027
1.175
1.336
1.509
1.698
1.904
2.129
2.376
2.646
2.942
3.268
3.627
4.022
4.457
4.937
5.466
6.050
0.695
7.406
8.192
9.060
10.02
11.08
12.25
13.54
14.97
16.54
18.29
20.21
22.34
24.69
27.29
30.16
33.34
36.84
40.72
45.00
49.74
54.97
60.75
67.14
74.20
48.27
53.34
58.96
65.16
72.01
1
48.75
53.88
59.55
65.81
72.73
0.0100
0.1102
0.2115
0.3150
0.4216
0.5324
0.6485
0.7712
0.9015
1.041
1.191
1.352
1.528
1.718
1.926
2.153
2.401
2.674
2.973
3.303
3.665
4.064
4.503
4.988
5.522
6.112
6.763
7.481
8.275
9.151
10.12
11.19
12.37
13.67
15.12
16.71
18.47
20.41
22.56
24.94
27.56
30.47
33.67
37.21
41.13
45.46
50.24
55.52
61.36
67.82
TABLE
1.
HYPERBOLIC
SINES
[sinh
x
=
$(e'
-
e-X)]
2
0.0200
0.1203
0.2218
0.3255
0.4325
0.5438
0.6605
0.7838
0.9150
1.055
1.206
1.369
1.546
1.738
1.948
2.177
2.428
2.703
3.005
3.337
3.703
4.106
4.549
5.039
5.578
6.174
6.831
7.557
8.359
9.244
10.22
11.30
12.49
13.81
15.27
16.88
18.66
20.62
22.79
25.19
27.84
30.77
34.01
37.59
41.54
45.91
50.74
56.08
61.98
68.50
3
0.300
0.1304
0.2320
0.3360
0.4434
0.5552
0.6725
0.7966
0.9286
1.070
1.222
1.386
1.564
1.758
1.970
2.201
2.454
2.732
3.037
3.372
3.741
4.148
4.596
5.090
5.635
6.237
6.901
7.634
8.443
9.337
10.32
11.42
12.62
13.95
15.42
17.05
18.84
20.83
23.02
25.44
28.12
31.08
34.35
37.97
41.96
46.37
51.25
56.64
62.60
69.19
4
0.0400
0.1405
0.2423
0.3466
0.4543
0.5666
0.6846
0.8094
0.9423
1.085
1.238
1.403
1.583
1.779
1.992
2.225
2.481
2.761
3.069
3.408
3.780
4.191
4.643
5.142
5.693
6.300
6.971
7.711
8.529
9.431
10.43
11.53
12.75
14.09
15.58
17.22
19.03
21.04
23.25
25.70
28.40
31.39
34.70
38.35
42.38
46.84
51.77
57.21
63.23
69.88
5
0.0500
0.1506
0.2526
0.3572
0.4653
0.5782
0.6967
0.8223
0.9561
1.099
1.254
1.421
1.602
1.799
2.014
2.250
2.507
2.790
3.101
3.443
3.820
4.234
4.691
5.195
5.751
6.365
7.042
7.789
8.615
9.527
10.53
11.65
12.88
14.23
15.73
17.39
19.22
21.25
23.49
25.96
28.69
31.71
35.05
38.73
42.81
47.31
52.29
57.79
63.87
70.58
6
0.0600
0.1607
0.2629
0.3678
0.4764
0.5897
0.7090
0.8353
0.9700
1.114
1.270
1.438
1.621
1.820
2.037
2.274
2.535
2.820
3.134
3.479
3.859
4.278
4.739
5.248
5.810
6.429
7.113
7.868
8.702
9.623
10.64
11.76
13.01
14.38
15.89
17.57
19.42
21.46
23.72
26.22
28.98
32.03
35.40
39.12
43.24
47.79
52.81
58.37
64.51
71.29
10.75
1 1.88
13.14
14.52
16.05
10.86
12.00
13.27
14.67
16.21
9
0.0901
0.1911
0.2941
0.4000
0.5098
0.6248
0.7461
0.8748
1.012
1.160
1.319
1.491
1.679
1.883
2.106
2.350
2.617
2.911
3.234
3.589
3.981
4.412
4.887
5.41 1
5.989
6.627
7.332
8.110
8.969
9.918
10.97
12.12
13.40
14.82
16.38
18.10
20.01
22.12
24.45
27.02
29.86
33.00
36.48
40.31
44.56
49.24
54.42
60.15
66.47
73.46
avg.
diff
100
101
103
106
110
116
122
130
138
15
16
17
19
21
22
25
27
30
33
36
39
44
48
53
58
64
71
79
87
96
11
12
13
14
16
17
19
21
24
26
29
32
35
39
43
47
52
58
64
71
__
If
x
>
5,
sinh
x
=
;(eX)
and
log,,
sinh
x
=
(0.4343)~
+
0.6990
-
1,
correct
to
four
significant figures.
MATHEMATICAL TABLES
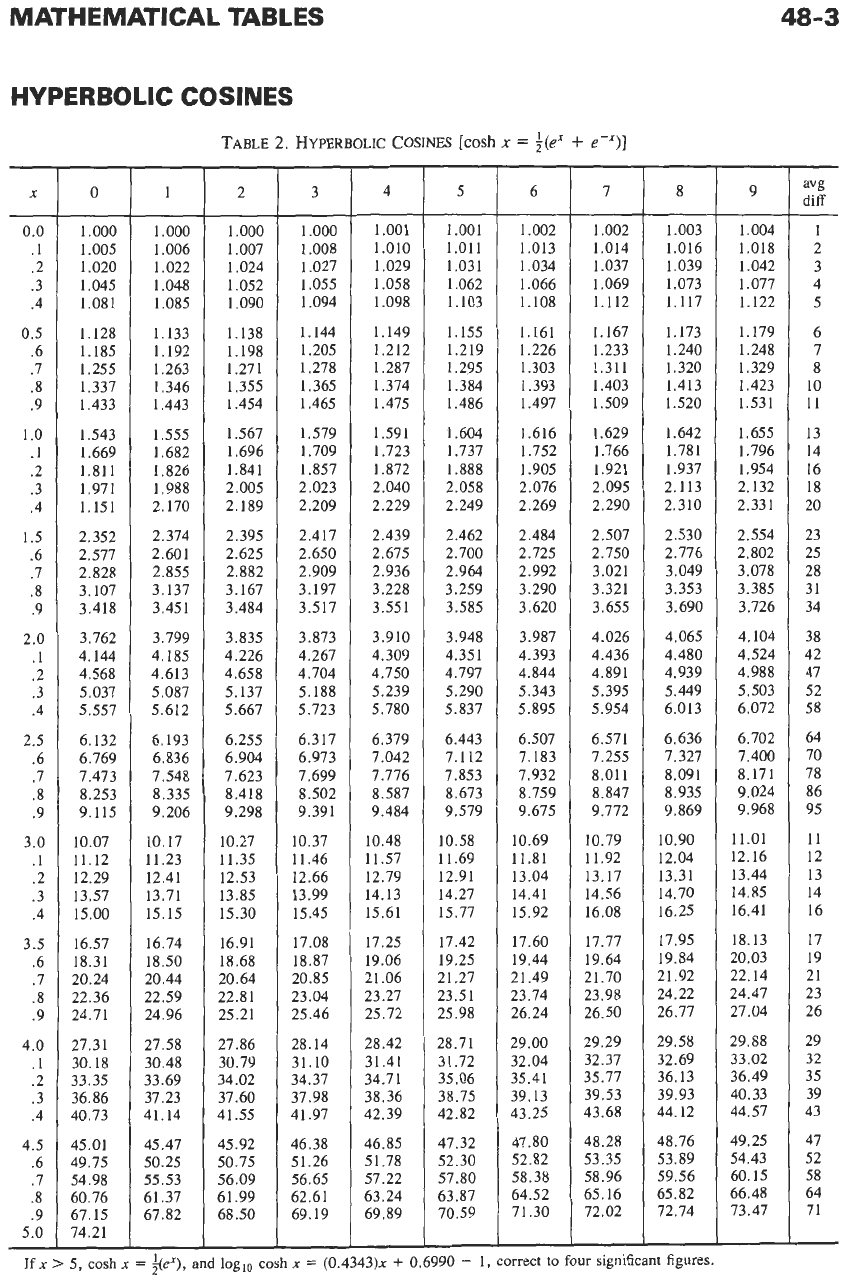
HYPERBOLIC COSINES
X
-
0.0
.1
.2
.3
.4
0.5
.6
.7
.8
.9
1
.o
.I
.2
.3
.4
1.5
.6
.7
.8
.9
2.0
.I
.2
.3
.4
2.5
.6
.7
.8
.9
3.0
.I
.2
.3
.4
3.5
.6
.7
.8
.9
4.0
.1
.2
.3
.4
4.5
.6
.7
.8
.9
5.0
If
x
-
0
1.000
1.005
1.020
1.045
1.081
1.128
1.185
1.255
1.337
1.433
1.543
1.669
1.811
1.971
1.151
2.352
2.577
2.828
3.107
3.418
3.762
4.144
4.568
5.037
5.557
6.132
6.769
7.473
8.253
9.115
10.07
11.12
12.29
13.57
15.00
16.57
18.31
20.24
22.36
24.71
27.31
30.18
33.35
36.86
40.73
45.01
49.75
54.98
60.76
67.15
74.21
1
1.000
1.006
1.022
1.048
1.085
1.133
1.192
1.263
1.346
1.443
1.555
1.682
1.826
1.988
2.170
2.374
2.601
2.855
3.137
3.451
3.799
4.185
4.613
5.087
5.612
6.193
6.836
7.548
8.335
9.206
10.17
11.23
12.41
13.71
15.15
16.74
18.50
20.44
22.59
24.96
27.58
30.48
33.69
37.23
41.14
45.47
50.25
55.53
61.37
67.82
TABLE
2.
HYPERBOLIC
COSINES
[cosh
x
=
$(ex
+
e-X)]
2
1
.ooo
1.007
1.024
1.052
1.090
1.138
1.198
1.271
1.355
1.454
1.567
1.696
1.841
2.005
2.189
2.395
2.625
2.882
3.167
3.484
3.835
4.226
4.658
5.137
5.667
6.255
6.904
7.623
8.418
9.298
10.27
11.35
12.53
13.85
15.30
16.91
18.68
20.64
22.81
25.21
27.86
30.79
34.02
37.60
41.55
45.92
50.75
56.09
61.99
68.50
3
1.000
1.008
1.027
1.055
1.094
1.144
1.205
1.278
1.365
1.465
1.579
1.709
1.857
2.023
2.209
2.417
2.650
2.909
3.197
3.517
3.873
4.267
4.704
5.188
5.723
6.317
6.973
7.699
8.502
9.391
10.37
11.46
12.66
13.99
15.45
17.08
18.87
20.85
23.04
25.46
28.14
31.10
34.37
37.98
41.97
46.38
51.26
56.65
62.61
69.19
4
1.001
1.010
1.029
1.058
1.098
1.149
1.212
1.287
1.374
1.475
1.591
1.723
1.872
2.040
2.229
2.439
2.675
2.936
3.228
3.551
3.910
4.309
4.750
5.239
5.780
6.379
7.042
7.776
8.587
9.484
10.48
11.57
12.79
14.13
15.61
17.25
19.06
21.06
23.27
25.72
28.42
31.41
34.71
38.36
42.39
46.85
51.78
57.22
63.24
69.89
5
1.001
1.011
1.031
1.062
1.103
1.155
1.219
1.295
1.384
1.486
1.604
1.737
1.888
2.058
2.249
2.462
2.700
2.964
3.259
3.585
3.948
4.351
4.797
5.290
5.837
6.443
7.112
7.853
8.673
9.579
10.58
11.69
12.91
14.27
15.77
17.42
19.25
21.27
23.51
25.98
28.71
31.72
35.06
38.75
42.82
47.32
52.30
57.80
63.87
70.59
6
1.002
1.013
1.034
1.066
1.108
1.161
1.226
1.303
1.393
1.497
1.616
1.752
1.905
2.076
2.269
2.484
2.725
2.992
3.290
3.620
3.987
4.393
4.844
5.343
5.895
6.507
7.183
7.932
8.759
9.675
10.69
11.81
13.04
14.41
15.92
17.60
19.44
21.49
23.74
26.24
29.00
32.04
35.41
39.13
43.25
47.80
52.82
58.38
64.52
71.30
7
1.002
1.014
1.037
1.069
1.112
1.167
1.233
1.311
1.403
1.509
1.629
1.766
1.921
2.095
2.290
2.507
2.750
3.021
3.321
3.655
4.026
4.436
4.891
5.395
5.954
6.571
7.255
8.01 1
8.847
9.772
10.79
11.92
13.17
14.56
16.08
17.77
19.64
21.70
23.98
26.50
29.29
32.37
35.77
39.53
43.68
48.28
53.35
58.96
65.16
72.02
-
8
1.003
1.016
1.039
1.073
1.117
1.173
1.240
1.320
1.413
1.520
1.642
1.781
1.937
2.113
2.310
2.530
2.776
3.049
3.353
3.690
4.065
4.480
4.939
5.449
6.013
6.636
7.327
8.091
8.935
9.869
10.90
12.04
13.31
14.70
16.25
17.95
19.84
21.92
24.22
26.77
29.58
32.69
36.13
39.93
44.12
48.76
53.89
59.56
65.82
72.74
9
5,
cosh
x
=
+(ex),
and log,,,
cosh
x
=
(0.4343)~
+
0.6990
-
1,
correct
to
four significant figures.
1.004
1.018
1.042
1.077
1.122
1.179
1.248
1.329
1.423
1.531
1.655
1.796
1.954
2.132
2.331
2.554
2.802
3.078
3.385
3.726
4.104
4.524
4.988
5.503
6.072
6.702
7.400
8.171
9.024
9.968
11.01
12.16
13.44
14.85
16.41
18.13
20.03
22.14
24.47
27.04
29.88
33.02
36.49
40.33
44.57
49.25
54.43
60.15
66.48
73.47
48-3
-
a%
diff
1
2
3
4
5
6
7
8
10
11
13
14
16
18
20
23
25
28
31
34
38
42
47
52
58
64
70
78
86
95
11
12
13
14
16
17
19
21
23
26
29
32
35
39
43
47
52
58
64
71
-
-
