Messerschmidt U. Dislocation Dynamics During Plastic Deformation

Подождите немного. Документ загружается.

392 9 Intermetallic Alloys

arrangement of the dislocations at high temperatures has to be a particular

core property.

A suitable model to describe the straight dislocation conﬁgurations is the

glide decomposition model originally suggested by Mills et al. [583] to explain

the behavior of 110 dislocations in NiAl as described in Sect. 9.4.4. Similar

processes may operate also in the other intermetallics with straight disloca-

tions listed earlier. Thus, this mechanism may perhaps be of more general

nature. For NiAl, it is proved by weak beam and high-resolution TEM. For

the other materials it is still speculative, though for several of the reactions

the calculations of the prelogarithmic factors of the elastic energy of the dis-

locations involved using anisotropic elasticity indicate a gain in energy. The

characteristic feature is the decomposition or dissociation by glide, where the

product dislocations do not lie on the glide plane of the parent dislocation,

thus making the dislocation core non-planar. The slip planes of all compo-

nents, i.e., the parent dislocation and the reaction products, intersect along

a single line deﬁning the preferred orientation of the dislocations. Since most

of the product dislocations cannot glide on the glide plane of the total dis-

location, these partials have to move by involving climb. The point defects

produced by one partial are then absorbed by the other, which is called con-

servative climb. At present, there are two models discussed in Sect. 9.4.4 for

estimating the dislocation velocity. They predict very diﬀerent dependencies

of the dislocation velocity on the dissociation width. To explain the ﬂow stress

anomaly, the models have to be extended by assuming that this width depends

on the dislocation velocity and the temperature in a way similar to the width

of the Cottrell atmospheres. The model is still hypothetic but it should be

worth spending more theoretical and experimental work on it.

At temperatures above the ﬂow stress peak, most intermetallic materials

behave in a way similar to other metals. The ﬂow stress is controlled by long-

range dislocation interactions where the dislocation structures are inﬂuenced

by recovery. In addition, climb seems to be a mode of dislocation motion.

In intermetallic materials, the contribution of athermal processes to the

total ﬂow stress is mostly an open question. Unlike in pure metals where the

dislocation substructures and densities are studied in great detail, very few

experiments are available giving information on the athermal part of the ﬂow

stress. For MoSi

deformed along 110, it was estimated that the athermal

part of the ﬂow stress in the low-temperature range may amount to 80%. A

similar situation may hold for the range of the anomalous increase of the ﬂow

stress. Thus, the increasing thermal component of the ﬂow stress may trigger

the dislocation generation thus inﬂuencing also the athermal stress component

as it was discussed in Sect. 5.2.2. More experimental results are desirable in

this respect.

Quasicrystals

In 1984, Shechtman, Blech, Gratias, and Cahn [635] detected diﬀraction

patterns of rapidly solidiﬁed aluminium manganese alloys with sharp peaks

having three-dimensional icosahedral symmetry. These diﬀraction patterns

enclose six symmetry axes with ﬁvefold symmetry. The observation was very

surprising since ﬁvefold symmetry violates the rules of crystallography based

on crystal structures formed by translational periodicity of a unit cell dec-

orated with the atoms. The fact that the diﬀraction patterns show sharp

reﬂections suggests that the materials have long-range order. This order com-

bined with missing translational symmetry can be explained by a new class

of materials with so-called quasiperiodic order, in addition to the crystalline

and amorphous states of solid matter. The new class of quasicrystals with

ideal atomic structures was introduced by Levine and Steinhardt [636] in the

same year as was the detection of the diﬀraction patterns with ﬁvefold sym-

metry, after early mathematical works on quasiperiodic structures and the

observation of modulated structures and incommensurate modulated phases.

Quasiperiodic structures can be formed by a number of diﬀerent proce-

dures. One consists in ﬁlling the plane or space by arranging two “unit cells”

called tiles according to so-called matching rules. In the two-dimensional case

the tiles are rhombi of equal edge length with angles of 36

◦

and 72

◦

and one or

two arrows at their edges. The matching rules require that adjacent tiles meet

with the same number and direction of the arrows. The resulting structures

were described by Penrose as early as in 1974 [637]. The quasiperiodic struc-

tures can be derived also by projection from a periodic higher-dimensional

hyperspace as will be described below. An introduction to these methods and

to the basic properties of quasicrystals is given by Janot [638].

Quasicrystals exhibit the same kinds of defects as crystals, i.e., point

defects like vacancies, dislocations, grain boundaries, etc., which may be con-

nected with elastic strains. In quasicrystals, the latter are called phonon

strains. In addition, the quasicrystalline order may be disturbed by violations

of the matching rules. These kinds of defects are speciﬁc to quasicrystals and

are termed phason strains. Dislocations in quasicrystals were ﬁrst observed

by Hiraga and Hirabayashi [639]. The dislocation strain ﬁeld includes both

394 10 Quasicrystals

phonon and phason strains. In a three-dimensional quasicrystal, it can be

described by a six-dimensional Burgers vector. Because of the missing peri-

odicity, the quasicrystalline structure is not intact after a dislocation has

moved, but a layer of phason faults is trailed if the temperature is not high

enough for annealing out these defects. Quasicrystals were therefore regarded

as intrinsically brittle.

Nevertheless, quasicrystals can be deformed plastically at high temper-

atures. The plastic deformation parameters were ﬁrst investigated on poly-

quasicrystals, e.g., [640–643]. The discovery of thermodynamically stable

ternary quasicrystalline phases [644] and the resulting possibility of grow-

ing large single quasicrystals [645] formed the basis for studying the intrinsic

plastic properties of quasicrystals. The observation of a drastic increase of the

dislocation density during the high-temperature deformation of Al–Pd–Mn

single quasicrystals pointed at the operation of a dislocation mechanism of

plastic deformation [646]. This view was conﬁrmed by the direct evidence of

dislocation motion during high-temperature in situ deformation experiments

in an high-voltage electron microscope (HVEM) [647]. Materials containing

quasicrystalline phases ﬁnd ﬁrst applications because of their particular sur-

face properties (e.g., [648]), the hydrogen storage capacity (e.g., [649]) or a

high strength up to high temperatures of alloys containing quasicrystalline

phases (e.g., [650, 651]).

In the following sections, the properties of dislocations in quasicrystals

and their role in the plastic deformation will be described. The treatment is

conﬁned to the two materials where experimental data of the author and his

coworkers are available, i.e., the stable phases Al–Pd–Mn with the icosahedral

structure and of Al–Ni–Co with the decagonal structure. To help understand-

ing the properties of dislocations, ﬁrst the quasiperiodic structures and their

construction by the cut and projection method are described.

10.1 Structure of Quasicrystals

Janner and Janssen [652] were the ﬁrst to present an analytical description

of incommensurate structures. It was later on extended by Duneau and Katz

[653] and Elser [654] to construct quasiperiodic structures by projecting a

higher-dimensional space onto the physical space. The method is illustrated

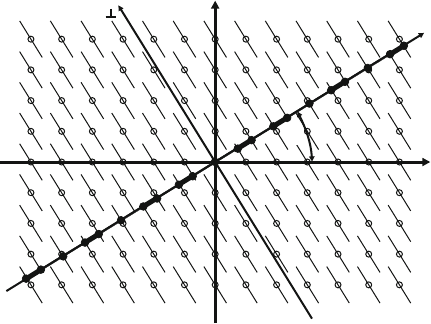
in Fig. 10.1 for the generation of a one-dimensional quasiperiodic lattice by

the projection from a two-dimensional square hyperlattice. In the origin of the

hyperlattice with the coordinate axes h

and h

, a second coordinate system

is placed having the coordinates x



and x

⊥

.Thex



axis deﬁnes the physical

space or, in quasicrystal terminology, the parallel space E



.Thex



axis is

rotated against the h

axis of the hyperspace by the angle α, which represents

an irrational slope tan α. Thus, except the origin the x



axis does not meet any

other lattice point. The x

⊥

axis deﬁnes the one-dimensional perpendicular or

orthogonal space E

⊥

. The one-dimensional quasiperiodic lattice in the physi-

cal space is generated by projecting the lattice points of the hyperspace onto

10.1 Structure of Quasicrystals 395

Fig. 10.1. Construction of a one-dimensional quasiperiodic point lattice from a

two-dimensional periodic lattice by the cut and projection method

the x



axis within a strip having the cross section parallel to x

⊥

equal to that

of the square unit cell. This is equivalent to decorating the hyperlattice points

with segments of the length of the strip and generating the lattice points

in real space at the intersections between the segments and the x



axis. In

Fig. 10.1, the lattice points in real space are indicated by full black circles. The

distances between the lattice points consist of two unit distances, short and

long ones characterized by thick and thinner lines along x



. These distances

follow a so-called Fibonacci sequence, which is not periodic, and which can

be generated by a recursive deﬂation rule where at each recursion step the

segments are replaced according to short → long and long → long + short.

A three-dimensional quasiperiodic structure is generated by the projection

of a six-dimensional hyperlattice onto the three axes in parallel space. Qua-

sicrystals can be quasiperiodic either in all three dimensions as the icosahedral

structure discussed below, or in two dimensions and periodic in the third as

the following decagonal structure, or in one dimension only. If the slope tan α

in Fig. 10.1 has a rational value, the matter is crystalline. A large periodicity

length corresponds to a large lattice constant. The structure is then called

an approximant. The respective alloys may be called structurally complex

intermetallic phases.

As will be shown below, the atoms in quasicrystals are arranged along

crystallographic directions and on crystallographic planes. Although these

structures lack periodicity, they produce sharp diﬀraction spots. The Fourier

transform of the point lattice in the six-dimensional hyperspace is again a

point lattice in the six-dimensional reciprocal space. It can be projected onto

the three-dimensional physical reciprocal space to yield the diﬀraction pat-

tern. As in this procedure all lattice points are projected and not only those

within a strip, there appears an inﬁnite number of diﬀraction spots. Since the

sensitivity of the recording medium is restricted, only suﬃciently strong spots

are recorded.

396 10 Quasicrystals

10.1.1 Quasicrystals with Icosahedral Symmetry

To obtain the icosahedral symmetry from a projection of the six-dimensional

hyperspace, the irrational slope of the axes of the parallel space with respect

to those of the hyperspace is set equal to the reciprocal value of the Golden

Mean tan α = τ

−1

,whereτ =



√

5+1



=1.61803 .... The icosahedron

implies six ﬁvefold axes, 10 threefold ones and 15 twofold ones as demon-

strated in Fig. 10.2. The reciprocal space exhibits icosahedral symmetry, too.

Therefore, the diﬀraction diagrams cannot be indexed by integers of three

basis vectors only. To index the three-dimensional parallel reciprocal space by

integers, six basis vectors are necessary, according to the integral indexing of

the six-dimensional hyperlattice. Depending on the choice of the basis vec-

tors, diﬀerent indexing systems have been proposed. The projection of the six

principal axes of the hyperspace yields the six ﬁvefold directions e

to e

the icosahedron. Taking the latter as the basis vectors conserves the indexing

of the six-dimensional reciprocal hyperspace.

Most frequently, icosahedral quasicrystals are indexed by applying the sys-

tem introduced by Cahn, Shechtman and Gratias [655]. It is based on the

three principal axes x, y, z of the cubic system of Fig. 10.2 parallel to three

orthogonal twofold axes. To denominate the irrational coordinates with inte-

ger indexes, the coordinates along the axes are written as h + τh



,etc.The

three components of the parallel subspace E



are related to the six coordinates

of the six-dimensional hyperspace n

to n

h + τh



=(n

− n

)+τ(n

+ n

)

k + τk



=(n

− n

)+τ(n

+ n

)

l + τl



=(n

− n

)+τ(n

+ n

). (10.1)

Fig. 10.2. Icosahedron with its three orthogonal twofold axes x, y,andz and the

six 5-fold axes e

to e

10.1 Structure of Quasicrystals 397

The components of the orthogonal subspace E

⊥

are given by



− τh =(n

+ n

)+τ(n

− n

)



− τk =(n

+ n

)+τ(n

− n

)



− τl =(n

+ n

)+τ(n

− n

). (10.2)

The vector (h + τh



,k+ τk



,l+ τl



) is abbreviated by (h/h



,k/k



l/l



)and

the vector (h



− τh, k



− τk, l



− τl)by(h



h, k



l). To obtain physical

g vectors in reciprocal parallel and perpendicular spaces, the index vectors

have to be multiplied by





2(2 + τ)



−1

,wherea

is the lattice constant of

the six-dimensional cubic primitive hyperlattice. For the stable i-Al–Pd–Mn

phase, a

=0.645 nm. The threefold symmetry axes result from the addition of

three neighboring ﬁvefold directions, e.g., e

+ e

,andthetwofoldones

from the sum of the two neighboring directions, e.g., e

+ e

. In addition,

there are two other distinctive types of poles, the 30 pseudo-twofold poles

between two neighboring twofold poles and 30 poles in the middle between

two orthogonal twofold poles, which correspond to the 110 poles of the cubic

crystal structure. Figure 10.3 illustrates experimental diﬀraction patterns of

these highly symmetric orientations.

To derive the real atomic structure of a quasicrystalline alloy, the lattice

points in the hyperspace are decorated with three-dimensional hypersurfaces

with an extension only in the perpendicular space E

⊥

. They consist of diﬀerent

shells with each shell corresponding to a particular chemical element. The

intersection of the cutting face of the projection with these shells determines

Fig. 10.3. Electron diﬀraction patterns of an i-Al–Pd–Mn single quasicrystal along

the main symmetry axes. (a)twofold,(b) threefold, (c)ﬁvefold,(d) pseudo twofold,

(e)“110”direction

398 10 Quasicrystals

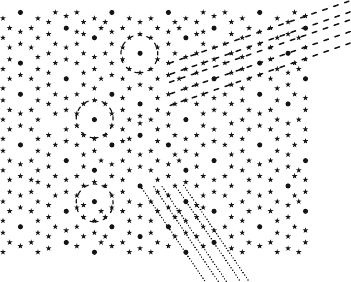
Fig. 10.4. Atom plane perpendicular to a ﬁvefold direction in i-Al–Pd–Mn after

the cluster model of Boudard et al. [656]

the element to be positioned at the respective site in the physical space E



The structure models are experimentally studied mostly by X-ray and neutron

diﬀraction, evaluating the intensities of hundreds of reﬂections. Figure 10.4

presents the arrangement of atoms on a plane perpendicular to a ﬁvefold

axis in i-Al–Pd–Mn, according to the study by Boudard et al. [656]. The

ﬁgure shows that the structure can be considered an arrangement of partly

penetrating clusters. Some of them are marked by circles. In the plane, they

consist of a central Mn atom and a ring of 10 Al atoms. Recent studies [657,

658] describe these structures by the decoration of a three-dimensional Penrose

tiling with so-called Mackay and Bergman type clusters with diﬀerent shells

of diﬀerent symmetry, i.e., dodecahedral, icosahedral, and icosidodecahedral.

These clusters contain up to 50 atoms and have a diameter of about 1 nm.

They are believed to be particularly strongly bound.

In addition to the cluster structure, Fig. 10.4 reveals that the atoms in the

quasicrystal structure are arranged in rows along crystallographic directions

marked by dashed and dotted lines, and these rows are located on crystallo-

graphic atomic planes, where the distances between the rows and between the

planes are not periodic. This crystallographic aspect was studied in [659]. Both

views on the same quasiperiodic structure have been discussed in [660]. They

are both important with respect to the dislocation properties to be treated in

the following sections.

10.1.2 Quasicrystals with Decagonal Symmetry

Decagonal quasicrystals are two-dimensional quasicrystals consisting of quasi-

periodic atomic planes with decagonal symmetry, which are stacked in a

periodic order. The respective diﬀraction patterns were ﬁrst observed in 1985

[661,662]. The stable phase Al-15at%Ni-15at%Co was ﬁrst synthesized by Tsai

et al. [663]. The diﬀraction patterns may be indexed by a linear combination

of multiples (H

) of ﬁve reciprocal basis vectors pointing at the corners of a

regular pentagon (e

∗

to e

∗

) and a sixth one in the direction of the periodic

10.1 Structure of Quasicrystals 399

axis (e

∗

). Since of the ﬁve vectors in the quasiperiodic plane only four are lin-

early independent, one of them can be omitted so that the diﬀraction vector

can be written as

g =(H

− H

) .

After the system by Steurer [664], the decagonal quasilattice is derived from

a ﬁve-dimensional hyperspace with the physical (parallel) space based on the

three orthogonal basis vectors v

, v

and the perpendicular space with

two orthogonal basis vectors v

, v

. The basis vectors of the ﬁve-dimensional

reciprocal lattice are then

∗

= a

∗



cos

2πi

, sin

2πi

, 0, cos

6πi

, sin

6πi



,i=1, ..., 4

∗

= a

∗

(0, 0, 1, 0, 0), (10.3)

and those of the physical lattice



cos

2πi

− 1, sin

2πi

, 0, cos

6πi

− 1, sin

6πi



,i=1, ..., 4

= a

(0, 0, 1, 0, 0), (10.4)

with a =1/a

∗

and a

=1/a

∗

. Figure 10.5 shows the projections a

∗

of the basis

vectors of the reciprocal lattice d

∗

onto the physical space. The periodic direc-

tion a

∗

points along the v

axis. The vectors a

∗

to a

∗

span the quasiperiodic

plane. The diﬀraction pattern of an Al-15at%Ni-15at%Co single quasicrystal

in Fig. 10.6 taken at the P2 pole (for this notation see [665]) with twofold

symmetry shows the periodic sequence of the quasiperiodic planes.

The atomic structure of the stable phase d-Al-15at%Ni-15at%Co was stud-

ied by X-ray diﬀraction [667]. It has the lattice constants a =0.3794 nm and

c =0.40807 nm. The structure consists of a periodic stacking of two quasiperi-

odic layers rotated against each other by 36

◦

. The basic structural building

elements corresponding to the clusters in icosahedral quasicrystals are colum-

nar clusters parallel to the tenfold axis. The central pentagons of the stacked

layers form pentagonal antiprismatic channels.

Fig. 10.5. Projection of the ﬁve-dimensional reciprocal basis vectors onto the

physical space according to Steurer [664]

400 10 Quasicrystals

(00002)

(00004)

(0-1104)

(100-10)

(01-100)

(1-11-10)

Fig. 10.6. Diﬀraction pattern of an Al-15at%Ni-15at%Co single quasicrystal taken

10.2 Defects in Quasicrystals

Quasicrystals generally exhibit the same types of lattice defects as crystals,

i.e., point defects like vacancies and interstitials [668–670], one-dimensional

defects as the dislocations [671], and two-dimensional defects like grain

boundaries [672], antiphase boundaries [673] and twins [674]. In addition,

quasicrystals contain phason defects mentioned already earlier.

10.2.1 Vacancies

Measurements of diﬀusion coeﬃcients of

Mn and

Fe in icosahedral Al–

Pd–Mn reveal a behavior similar to that in metals, pointing at a vacancy

mechanism of diﬀusion [668]. Thus, the thermal vacancy concentration can be

described by an equation like (4.76). The formation and migration enthalpies

of vacancies were determined by time-diﬀerential dilatometry to amount to

ΔH

=0.6eV and ΔH

=0.8 eV [675]. Thus, they are similar to those in

pure aluminium. Positron annihilation spectroscopy reveals a neighborhood

of the vacancies dominated by Al atoms [676]. However, Pd and Mn diﬀuse

by several orders of magnitude slower than Al [677]. In addition to thermal

vacancies, structural vacancies of a concentration of about 10

−3

are observed

in Al–Pd–Mn. Some papers (e.g., [678]) suggest that structural vacancies in

the center of clusters of 12 Al atoms stabilize the quasicrystalline phase.

10.2.2 Phason Defects

If in physical space part of a quasicrystal is shifted with respect to the rest,

there does not exist a three-dimensional displacement vector leading to an

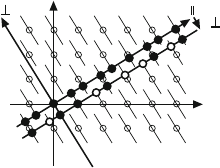
10.2 Defects in Quasicrystals 401

Fig. 10.7. Generation of phason faults by a displacement in the perpendicular space

undistorted lattice, because of the missing periodicity. Along the cutting plane,

the matching rules are violated. The corresponding defects are called pha-

sons. The process can be illustrated by the cut and projection procedure as

shown in Fig. 10.7 for the generation of a one-dimensional quasiperiodic struc-

ture from a two-dimensional periodic lattice. Lattice defects are described

by their displacement ﬁeld in the higher-dimensional hyperspace. A gen-

eral displacement U can then be split into components in both subspaces

according to

U = u



)+u

⊥



), (10.5)

which are called phonon and phason displacements. As all physical properties

of quasicrystals depend only on the coordinates in physical (parallel) space,

both displacements depend only on x



. The respective strains are the phonon

and phason strains. If the shift vector U is a lattice vector in the hyperspace,

there results an undisturbed quasicrystal. In other cases, the displacement

vectors can be split according to (10.5). Shifts parallel to the x



axis pro-

duce an elongation or contraction of the distances between the atoms, i.e.,

an elastic or phononic strain. However, displacements of the lattice points of

the hyperlattice parallel to the x

⊥

axis, which, in Fig. 10.7, is identical with

ashiftu

⊥

of the x



axis into x





, lead to a change in the sequence of lat-

tice points since now other decorations of hyperlattice points intersect the



axis. In the new Fibonacci sequence, many atoms marked by full circles

are in the same position as in the original sequence. Some, however, which

are marked by open circles, do not ﬁt the original quasiperiodic order and are

called phason ﬂips. The phason ﬂips represent violations of the matching rules

of the quasiperiodic lattice. Phason ﬂips can appear individually as random

phasons. Spatial variations of u

⊥

result in collective ﬂipping of unit cells in

worms causing mismatches at the boundaries of the ﬂipped areas. Since real

quasicrystals are always alloys of two or more constituents, phason disorder

is also connected with chemical disorder.

The properties of defects in quasicrystals were discussed in detail in [679].

Arrangements of atoms in a two-dimensional array were calculated using the

density-wave method, which is an additional way to generate quasiperiodic

lattices ([680] and other references in [679]), and were compared with results