Messerschmidt U. Dislocation Dynamics During Plastic Deformation

Подождите немного. Документ загружается.

372 9 Intermetallic Alloys

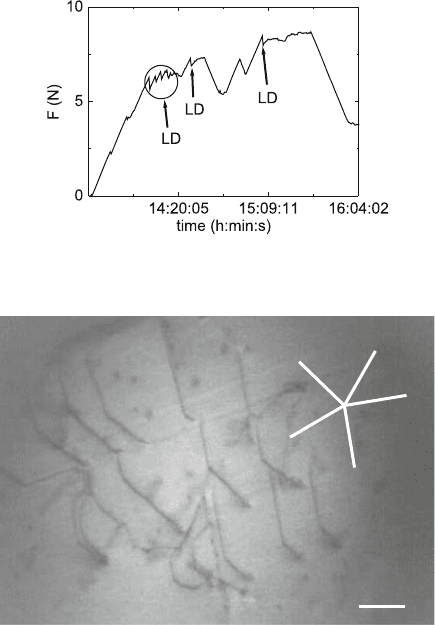
Fig. 9.39. Load–time recording of the in situ straining experiment on MoSi

Videos 9.16 and 9.17 with sudden load drops LD. Data from [619]

3-31

– 33-1

00-1

1-10

1-11

1 µm

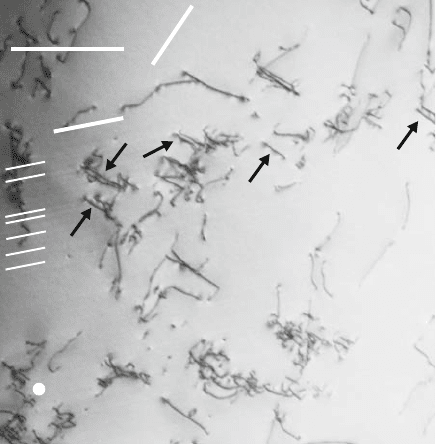
Fig. 9.40. Section of a frame from Video 9.16 showing dislocation motion in MoSi

at 990

◦

C. The c axis denoted by [00

1] lies in the image plane, the other bars mark

the projections of the indicated directions onto the image plane. The Burgers vector

is 1/2[1

11]. From the work in [288]

very high velocities. Later on, during continuous deformation, the dislocations

moved in a viscous way as demonstrated in the following video clip taken at

almost 1,000

◦

Video 9.16. Dislocation motion and generation in MoSi

deformed at 990

◦

Calong

[201]: The dislocations are mostly straight along crystallographic orientations, which

are indicated in Fig. 9.40. The preferred orientations of the dislocations with an

angular shape are [1

10] and [3

31], i.e., 60

◦

and edge at the 1/2[1

11] Burgers vec-

tor, as in the macroscopic experiments. During the motion in direction of the slip

traces imaged in weak contrast, curved segments and superkinks form, which move

along the dislocations as marked by M in the video. At the dislocation labeled K

in Fig. 9.41, several superkinks are visible. When moving at higher velocities, the

dislocations prefer the 60

◦

character.

9.6 Molybdenum Disilicide 373

Fig. 9.41. Section of a frame from Video 9.16 showing the localized dislocation

source

At S in the lower part of the video, a one-ended localized dislocation source as

described in Sect. 5.1.1 and Fig. 5.1b generates new dislocations. The source is also

shown in Fig. 9.41. It consists of one arm P lying on the primary (110) slip plane,

and of a ﬁxed segment F on another plane, therefore having a low mobility.

In MoSi

, cross slip of dislocations with 1/2111 Burgers vectors seems to be

very restricted. It has never been observed in the in situ experiments that these dis-

locations cross slip from their {110} slip planes onto the {011} planes, which contain

the same Burgers vector. The movable arm on a plane parallel to that of the segment

P is marked by arrows. With each revolution of the moving branch, one dislocation

is emitted to the right and another to the left. While the dislocations moving to the

left leave the frame of the recording, the dislocations emitted to the right pile up

in the stress ﬁeld of other pre-existing dislocations. As described in Sect. 5.2.1, the

piled-up dislocations cause a back stress which shields the source. Later on, these

dislocations move away and the source operates again. The generation of several

tens of dislocations has been observed.

Usually, intrinsic pinning agents which cause dislocation generation are jogs in a

screw dislocation, which have edge character and cannot glide in the forward direc-

tion of the dislocation motion. The observed source in MoSi

is insofar particular

as the pinning segment is located in a 60

◦

dislocation, where its pinning is due to a

low mobility on a plane away from the easy {110} slip plane.

Some details of the motion of dislocations with 1/2111 Burgers vector

are also shown in the following video.

Video 9.17. Dislocation motion in MoSi

deformed at 990

◦

Calong[201]: In this

video sequence, the segments extending along [3

31] develop several superkinks and

move faster than those along [1

10] so that the latter extend. Later on, the lower

part of the leading dislocation bows out. The bowing segment is bordered by a jog

labeled J. The cusp in the dislocation line forming at the jog causes line tension

forces on the jog driving it in upward direction along the [1

10] segment. As the

jog itself has edge or mixed character, it cannot glide in this direction. Therefore

climb must have contributed to the sidewise motion of the jog. Later on, part of the

dislocation emerges through the foil surface.

374 9 Intermetallic Alloys

In conclusion, dislocations with 1/2111Burgers vectors arrange mostly in

straight crystallographically oriented conﬁgurations, both within the range of

the low-temperature decrease of the ﬂow stress as well as in the anomaly range.

However, a transition occurs from the dominating 60

◦

dislocations along 111

at low temperatures to those along 110 at high ones.

At temperatures above the ﬂow stress maximum, i.e., above 1,000

◦

C, in

addition to the 1/2111 dislocations those with 100 Burgers vectors are

observed more frequently than at lower temperatures. They occur preferen-

tially as Frank loops.

Deformation Along 110

In this orientation, dislocations with 1/2111 Burgers vectors have zero

orientation factors. Therefore, dislocations with 100 Burgers vectors are

activated. An example of the microstructure produced in the low-temperature

range at 380

◦

C was shown in Fig. 2.6 including the analysis of the 100 Burg-

ers vectors using the contrast extinction rule (Sect. 2.3). Figure 9.42 presents

the dislocation structure of a specimen cut parallel to the (110) cross-sectional

face, taken from the same deformation experiment. In this projection, all four

1 µm

(–110)

[110]

Fig. 9.42. Dislocation microstructure of MoSi

deformed along [110] at 380

◦

Cfrom

the same deformation experiment as Fig. 2.6. Foil plane parallel to the (110) cross

section plane. From [15]. Copyright Wiley-VCH (2005)

9.6 Molybdenum Disilicide 375

2 μm

(1-10)

[-1-11]

tr(101)

tr(011)

Fig. 9.43. Microstructure in MoSi

after deformation along 110 at 606

◦

Cby0.2%.

Foil plane parallel to the (001) side face of the compression specimen. The straight

lines marked tr indicate the directions of the traces of the respective planes imaged

edge-on. From [15]. Copyright Wiley-VCH (2005)

{101} slip planes are inclined to the foil plane (in contrast to Fig. 2.6b and

d, where two of the four slip planes are imaged edge-on). It is obvious that

the dislocations are curved at this temperature at the end of the normal

low-temperature range of the ﬂow stress. The dislocation density was esti-

mated to amount to about 2.8 × 10

−2

The dislocation structures in the lower part of the anomaly range are

documented in Figs. 9.43 and 9.44 of a specimen deformed at 606

◦

C. The foil

is cut parallel to the (001) side face of the compression sample. In Fig. 9.43, the

specimen is imaged near the [

11] pole with g =(1

10) so that all dislocations

with 100 Burgers vectors are visible. Many dislocations are straight and

oriented parallel to the traces of the (101) and (011) planes, which are imaged

edge-on in the projection of the ﬁgure. Thus, it may be assumed that these

dislocations extend on these slip planes. Figure 9.44 presents a specimen area

close to that of Fig. 9.43 imaged with g =(1

10) near the [001] pole where all

dislocations are visible. These dislocations have again 100Burgers vectors. In

the projection of the ﬁgure, most dislocations are also straight and oriented

parallel to either the [1

10] direction, indicated by the g vector, or to the

perpendicular [110] direction. Thus, these dislocation lines extend along 111

directions. It is argued in [15] that most of the dislocations which are not

parallel to the traces in Fig. 9.43 are also aligned parallel to 111 directions.

376 9 Intermetallic Alloys

[001]

(1-10)

1µm

Fig. 9.44. Microstructure of the same specimen as Fig. 9.43 taken near the [001]

pole. From [15]. Copyright Wiley-VCH (2005)

1 μm

[1-10]

(110)

pr[111]

pr[11-1]

Fig. 9.45. Dislocation structure after deformation at 672

◦

C by 0.25%. The

straight lines marked pr indicate the directions of the projections of the indicated

orientations. From [15]. Copyright Wiley-VCH (2005)

The dislocation structures formed at a small strain at a higher temperature

within the anomaly range (672

◦

C) are displayed in Fig. 9.45 taken near the

10] pole. The compression axis is parallel to the (110) g vector. All four

{101} slip planes are inclined to the foil plane at equal angles. The images

show that the dislocations have angular shapes with segments appearing in the

projections of the 111 directions. Burgers vector and stereometric analysis

have shown that practically all dislocations are parallel to the projections of

the four 111 directions. It may therefore be concluded that in the range

9.6 Molybdenum Disilicide 377

1 µm

(110)

[001]

[100]

Fig. 9.46. Dislocations during in situ straining in an HVEM at 475

◦

Calong110

of a specimen pre-deformed at 606

◦

C. From [15]. Copyright Wiley-VCH (2005)

of the ﬂow stress anomaly, the dislocations with 100 Burgers vectors show

distinctly preferred orientations along 111.

In situ straining experiments were tried on pre-deformed specimens at dif-

ferent temperatures. Only one test at 475

◦

C near the ﬂow stress minimum

was successful. Figure 9.46 presents the microstructure obtained. Most dislo-

cations originate from the pre-deformation. Dislocations having moved during

the in situ loading have produced slip traces, which are visible as weak bright

lines. Some of them are marked by short white lines near the left edge of

the ﬁgure. At the [001] pole, the slip traces run in [100] directions, i.e., they

belong to the (011) and (0

11) slip planes. Some of the dislocations which

had moved are marked by black arrows. These dislocations are straight. Their

projections follow the [

110] direction. Thus, the dislocation lines should be

oriented again along 111 directions. Accordingly, this single successful in

situ experiment conﬁrms the result of the above post-mortem studies that

the active dislocations are straight and oriented along 111 at intermediate

temperatures.

In the high-temperature range above the ﬂow stress peak, the dislocations

are no longer straight and crystallographically oriented but smoothly bow out.

At high dislocation densities, they form dislocation bands by the interaction

between dislocations on (101) and (

101) planes, which both contain the [010]

Burgers vector.

378 9 Intermetallic Alloys

Stacking Faults

In MoSi

, stacking faults on (001) habit planes were described in a number

of papers, e.g., [623–625]. Taking into account the results on faults observed

after deformation at high temperatures, speciﬁc climb dissociation reactions

were considered, e.g., in [616,626], leading to APBs and CSFs on (001) planes.

As a second process, the formation of grown-in condensation faults on (001)

planes is considered due to a loss of Si during the growth of MoSi

single

crystals at temperatures up to 1,600

◦

C [624,625]. These faults are bordered by

Frank type dislocations having a Burgers vector parallel to [001]. During the

in situ straining experiments described above, faults on (001) planes formed

instantaneously. These faults were studied in detail in [627].

The faults were created principally during in situ straining or heating in the

HVEM at temperatures between 440 and 1,000

◦

C and only if dislocations with

1/2111 Burgers vectors were present. These dislocations may originate either

from in situ loading or from a pre-deformation in macroscopic experiments.

Figure 9.47 presents an example of the formation of such faults during in situ

annealing at 630

◦

C. The faults are generated so quickly that the process itself

has never been recorded.

The displacement vector R

of the faults and the Burgers vectors of the

bordering dislocations have been analyzed by the methods of TEM diﬀraction

contrast, e.g., the contrast extinction rule (2.9) in Sect. 2.3. An example of a

fault bounded by dislocations A and B is presented in Fig. 9.48. The details

of the analysis are described in [627] including further ﬁgures. The analy-

sis clearly showed that the displacement vector R

equals either 1/6[001] or

1/2[001], which both characterize intrinsic stacking faults, and that the Burg-

ers vector of one dislocation bordering each fault is parallel to [001] but that

the other dislocation does not have the same Burgers vector, see in particu-

lar Fig. 9.48g where dislocation B is extinguished, but A is not. The Burgers

vector of the second dislocation should be parallel to [110]. Although the

whole analysis in [627] is not unambiguous, it is argued that the Burgers

vectors of the bordering dislocations are 1/2[001] and 1/2[110]. Thus, these

defects cannot be stacking faults, and produced by the condensation of vacan-

cies due to a loss of Si, which on all edges should be surrounded by Frank

partial dislocations. Besides, the instantaneous formation of the defects con-

tradicts the creation by a diﬀusion process. Since the generation of the defects

is bound to the presence of dislocations with 1/2111 Burgers vectors, the

best explanation of their formation is the dissociation of these dislocations

according to

1/2[111](1

10) → 1/2[001](1

10) + 1/2[110](001). (9.8)

The reaction leads to faults with a fault vector equal to the absolute value

of the Burgers vector of the Frank-type partial with R

= −1/2[001]. The

faults can be created either by climb of the Frank-type dislocation with a

1/2[001] Burgers vector, or by glide of the partial dislocation with the 1/2[110]

9.6 Molybdenum Disilicide 379

p [110]

1µm

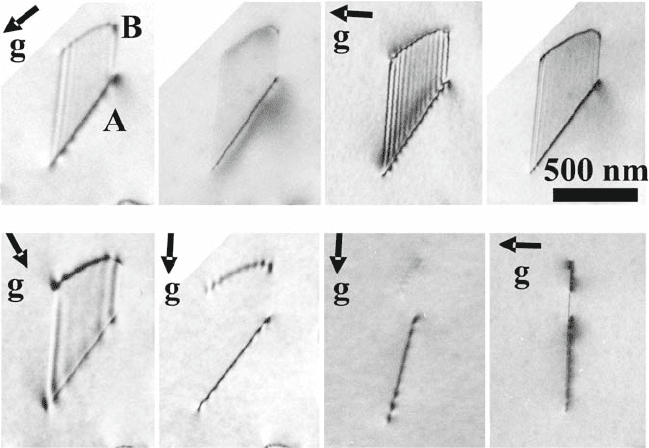
Fig. 9.47. Formation of planar faults on (001) planes on dislocations with a 1/2[111]

Burgers vector during an in situ annealing experiment on an MoSi

single crystal at

630

◦

C. (a) Microstructure with 1/2[111] dislocations after macroscopic compression.

Beam direction near n = [010], g = (200). p is the projection of the [110] direc-

tion onto the image plane. Dislocations oriented along this direction are marked by

arrows.(b) Sudden formation of faults labeled by arrows during in situ annealing

at about 630

◦

C. g =(

101). The faults are imaged edge-on. (c) The faults after

post-mortem analysis at n =[0

1] and g = (200). After [627]. Copyright Taylor &

Francis Ltd. (2002)

Burgers vector, both on the (001) plane. The indexes in parentheses mark the

slip planes of the respective dislocations. Their 110 intersection line is the

preferred orientation of the initial dislocation for dissociation. The fault vector

corresponds to a removal of three (001) layers, two Si layers and one Mo layer,

without a loss of stoichiometry.

The planar faults are not created on all dislocations with 1/2111 Burgers

vectors. The width of the faults scatters over a wide range. However, faults

with a large width appear particularly during in situ straining experiments

380 9 Intermetallic Alloys

abcd

ef gh

Fig. 9.48. Contrast analysis of a planar fault on a (001) plane and its bordering

partial dislocations A and B in MoSi

.(a) g = (213) at n =[03

1]. (b) g =2× (213)

at n =[03

1]. (c) g = (013) at n =[03

1]. (d) g =3× (013) at n =[03

1]. (e)

g =(2

3) at n =[03

1]. (f) g = (200) at n =[03

1]. (g) g = (200) at n = [010]. (h)

under the applied load. The formation of the planar faults on 1/2111 dislo-

cations arranged along 110 suggests that the cores of these dislocations are

unstable and tend to dissociate. The same dislocations dominate the plastic

deformation in the range of the ﬂow stress anomaly. The consequences will be

described in Sect. 9.6.4.

9.6.3 Macroscopic Deformation Parameters

Figure 9.49 displays typical stress–strain curves up to small plastic strains of

MoSi

single crystals deformed along the soft [201] direction. The yield stress

shows the typical three temperature ranges, a region of the normal decrease

below 500

◦

C, the anomaly range up to 990

◦

C and a normal high-temperature

range above that temperature. The stress–strain curves are smooth with a

yield drop eﬀect, except in the anomaly range where plastic instabilities (ser-

rated yielding) occur. For deformation along [110], the curves are smooth at

all temperatures with one exception. An example of the deformation at 738

and 726

◦

C was shown in Fig. 2.2b.

The temperature dependence of the yield stress is presented in Fig. 9.50

forthetwoloadingaxes.Bothcurvesshow the three characteristic ranges.

In general, the ﬂow stresses for loading along 110 are higher than those

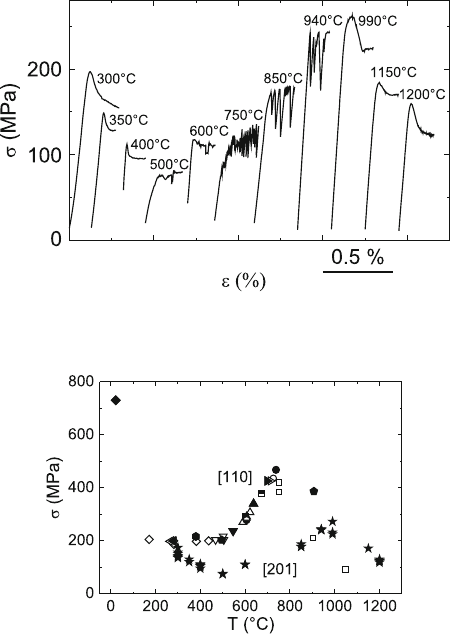
9.6 Molybdenum Disilicide 381

Fig. 9.49. Stress–strain curves of MoSi

single crystals deformed along the soft

201 direction at diﬀerent temperatures. Data from [288]

Fig. 9.50. Temperature dependence of the yield stress of MoSi

single crystals

deformed along 201 (ﬁvefold stars)and110 (full symbols for data from the

ﬁrst loading of a specimen, open symbols for data taken after temperature changes

corrected for work-hardening). Data from [15]

for 201, and the ﬂow stress peak is shifted to a lower temperature. (The

orientation factors are similar, m

=0.4for201 and m

=0.46 for 110.)

The strain rate sensitivity r of the ﬂow stress was again measured by stress

relaxation tests. Some examples of the deformation along 110 are shown in

Fig. 9.51. At room temperature, the curve exhibits the normal bending toward

the stress axis. At increasing temperature (281

◦

C), the curves with normal

curvature become very steep, corresponding to low values of r. In the anomaly

range at 502

◦

C, the curve is still very steep, but it starts to show an inverse

curvature with increasing strain rate sensitivity at decreasing strain rate or

stress. At higher temperatures in the anomaly range (638

◦

C, 698

◦

C), the

curves are steep at the beginning but then clearly show the inverse curva-

ture. Only at low strain rates, the curves bend back to the normal curvature