Messerschmidt U. Dislocation Dynamics During Plastic Deformation
Подождите немного. Документ загружается.

362 9 Intermetallic Alloys
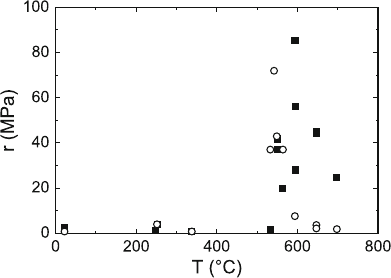
Fig. 9.35. Temperature dependence of the strain rate sensitivity r measured from
the slope of stress relaxation curves at relaxation (strain) rates of ˙ε =10
−5
s
−1
(filled
squares)and10
−7
s
−1
(open circles). Data from [8]
towards the stress axis, corresponding to most obstacle mechanisms. For a
narrow range within the anomaly range (at 533 and 542
◦
C), the curves have
a typical two-stage shape with an inverse curvature bending away from the
stress axis. As outlined in Sect. 4.11, the inverse curvature points at a mech-
anism with the dynamics of the Cottrell effect for the flow stress anomaly.
Values of the strain rate sensitivity r of the flow stress shown in Fig. 9.35
were evaluated from the slope of the stress relaxation curves at strain rates
of 10
−5
and 10
−7
s
−1
. They are very small up to about 530
◦
Candshowa
maximum at about 600
◦
C, i.e., above the flow stress peak. In the anomaly
range, the values measured at the strain rate of 10
−7
s
−1
are higher than those
at 10
−5
s
−1
, in agreement with the inverse curvature of the relaxation curves.
In the high-temperature range, the behavior is normal as expected from the
normal temperature dependence of the flow stress. Strain rate change exper-
iments over a wide range of strain rates between 5 × 10
−7
to 10
−4
s
−1
show
zero strain rate sensitivity at room temperature, 250 and 533
◦
C.
9.5.3 Deformation Mechanisms
The following discussion of the processes controlling the deformation of FeAl
is divided according to the temperature ranges, room temperature, the range
of the flow stress anomaly, and the range above the peak temperature.
Room Temperature
The in situ straining experiments show dislocations with 111 Burgers vectors
slightly bowing out between obstacles of an average distance of l ≈ 0.1 μm=
200 b (Fig. 9.29) and moving in a jerky way (Video 9.12). This is a mechanism
typical of low temperatures also in other intermetallic alloys. In principle, the
9.5 FeAl 363
obstacles may be jogs as in NiAl (Sect. 9.4.4) or small precipitates as in TiAl
(Sect. 9.3.4). In situ straining experiments on FeAl at room temperature were
performed earlier, yielding similar results [592].
At room temperature, the strain rate sensitivity r exhibits a normal depen-
dence on the strain rate. Using (4.9), the value of r =2.6MPaat ˙ε =10
−5
s
−1
(Fig. 9.35) is related to an activation volume of V ≈ 3.7 × 10
−27
m
3
=30b
3
.
In microscopic terms, the activation volume is given by V =Δdlb (4.4)
yielding an activation distance of Δd ≈ 0.15 b. This is a normal value for dis-
location motion controlled by localized obstacles like small precipitates (see
the similar estimates for ZrO
2
(Sect 7.3.5), Al–Zn–Mg (Sect. 8.1.1) or TiAl
(Sect. 9.3.4)). The very jerky motion over large distances indicates that the dis-
location motion is of almost athermal nature (Fig. 4.18), i.e., that the Peierls
mechanism, which frequently acts at low temperatures, is not important.
Flow Stress Anomaly
As discussed in [593], a number of models were established to explain the flow
stress anomaly in B2 ordered FeAl crystals. Since macroscopic deformation
between room temperature and the peak temperature is carried by disloca-
tions with the 111 Burgers vector (Sect. 9.5.1), these dislocations must be
responsible for the anomaly. The models include:
• Cross slip of dislocations with 111 Burgers vectors from their {110} slip
plane onto {112} planes where they get pinned, by analogy with Kear–
Wilsdorf locks in Ni
3
Al [594]
• Local decomposition of dislocations with 111 Burgers vectors into par-
tials with 001 and 110 Burgers vectors, which impedes the dislocation
motion [595]
• Localized climb of the antiphase boundary-coupled partials [596] according
to a model originally proposed to explain the flow stress anomaly in β brass
[584]
• Hardening owing to the high concentration of thermal vacancies at the
temperatures of the flow stress anomaly (vacancy hardening model) [593]
based on the observation that the anomaly occurs only in specimens in
which the high excess vacancy concentration originating from the crys-
tal preparation is annealed out by long-time annealing at relatively low
temperatures [597]
The in situ straining experiments described earlier show a viscous motion
of straight oriented dislocations. Such a behavior is not considered in the
literature on deformation of B2 Fe–Al. The viscous motion contradicts all
pinning/unpinning mechanisms with jerky dislocation motion like the first
three models listed above.
From the literature, it is obvious that during the deformation of FeAl at
high temperatures point defects play an essential role, e.g., the structural
defects originating from deviations from stoichiometry [598]. The effects of

364 9 Intermetallic Alloys
thermal vacancies are considered in the vacancy hardening model of George
and Baker [593], mentioned above, and in other related papers [599–601]. In
this model, individual thermal vacancies appearing in the range of the flow
stress anomaly are supposed to pin the dislocations as localized nondiffus-
ing obstacles to be treated by the theory of localized obstacle hardening as
described in Sect. 4.5.1. There are several experimental observations support-
ing the importance of thermal vacancies in connection with the flow stress
anomaly. In experiments with fast up-heating to the deformation tempera-
ture, the flow stress anomaly occurs only after an incubation time of the
order of some minutes. This time equals the time necessary to establish the
equilibrium concentration of thermal vacancies [602]. Besides, after quenching
down from temperatures in the anomaly range, the specimens show the same
flow stress at room temperature as those deformed at the annealing temper-
atures [600]. However, vacancies should not act as fixed localized obstacles
at the high temperatures in the range of the anomalous increase of the flow
stress as will be discussed below.
It is difficult to estimate the interaction strength between a vacancy and
a dislocation. Considering the vacancy as an inclusion of zero bulk modulus,
the maximum interaction energy is given by (e.g., [603])
ΔG
0
=
9K
e
V
16π
2
1+ν
1 − ν
,
where V is the volume of the vacancy taken as V = a
3
/2, and ν is Poisson’s
ratio (ν =0.384 [604]). K
e
is the energy factor of the edge dislocation with
111 Burgers vector on the {110} plane. It replaces the shear modulus. K
e
is
calculated using the anisotropic elastic constants from [591] mentioned above.
With these data, K
e
= 108 GPa and ΔG
0
=1.03 eV are obtained. Assuming,
for simplicity, a triangular interaction profile of the width of the absolute value
of the Burgers vector, the resulting maximum force is given by
F
0
=ΔG
0
/(0.5 b).
This yields F
0
=6.6 × 10
−10
N. To decide whether Friedel or Mott statistics
has to be applied, the parameter ξ
0
can be estimated from (4.52). For the low
concentration of vacancies of c ≈ 3×10
−4
at the flow stress peak [605] and with
the width of the obstacles x
0
≈ b, the square lattice distance l
sq
= ac
−1/2
/2,
and the energy factor of the edge dislocation mentioned above, it follows that
ξ
0
≈ 0.07 1 so that Friedel statistics can be applied. Then, the contribution
of the obstacles to the flow stress at zero temperature is given by (4.56).
Thus, σ
∗
0
= τ
∗
0
/m
s
= 170 MPa with the orientation factor m
s
=0.44 for
the (101)[11
¯
1] slip system. In terms of the Friedel model, the contribution of
solution hardening to the flow stress shows a strong temperature dependence
with a limiting temperature
T
0
=
ΔG
0
k ln( ˙γ
0
/ ˙γ)
,
9.5 FeAl 365
above which the contribution is small. k is again Boltzmann’s constant, ˙γ the
(shear) strain rate and ˙γ
0
the pre-exponential factor in the Arrhenius equation
of the strain rate (4.8). With a characteristic value of ln( ˙γ
0
/ ˙γ) ≈ 25, T
0
becomes about 200
◦
C. Consequently, vacancies of the estimated concentration
at the flow stress peak may contribute to the flow stress at low temperatures,
e.g., quenched-in vacancies at room temperature, but they should not cause
the flow stress anomaly at much higher temperatures. The fact that such small
and relatively weak obstacles as individual vacancies are easily surmounted
at high temperatures by the aid of thermal activation is generally neglected
in the literature of the vacancy hardening model of the flow stress anomaly
in FeAl. Vacancy agglomerates, which may act also at higher temperatures,
usually occur at much lower concentrations than the individual vacancies do.
Several experimental results can well be interpreted by dynamic strain age-
ing. Effects of strain ageing were observed in FeAl in several experiments (e.g.,
[606–608]), but not in all. In the experimental material above, this concerns, in
particular, the occurrence of the flow stress anomaly itself, the inverse behavior
of the strain rate sensitivity (Fig. 9.35), and the appearance of serrated yield-
ing (Fig. 9.33) connected with slip localization. According to [608], serrated
yielding depends on the orientation of the loading axis. The present orienta-
tion is in the range of unstable slip. Serrated yielding is certainly favored in
single crystals in single slip orientation where slip localization is promoted.
It is also supported in a stiff testing machine used here, where sudden strain
increments cause large stress drops. As described in Sect. 5.3, the so-called
strain rate softening instabilities do not require a negative strain rate sensi-
tivity. It is sufficient if the strain rate sensitivity is small, which is fulfilled in
the present experiments.
It was discussed in Sect. 4.11 that diffusion processes in the dislocation
cores like the Cottrell effect may cause a flow stress anomaly. This idea was
applied in Sect. 9.3.4 to the anomaly in γ TiAl. The respective formulae are
(4.100) for the maximum contribution of this effect to the flow stress, and
(4.99) for the relation between the critical strain rate and the diffusion coef-
ficient and the temperature. It may be assumed that the diffusing defects are
the Fe vacancies. The interaction strength β is given by (3.32) for solutes
with a hydrostatic stress field. By comparing this formula with (14–42) in
[12] it may be concluded that for vacancies ΔΩ is given by the relaxation
volume of the vacancy. Since it is not known, it is assumed that it amounts
to 30% of the atomic volume, i.e., ΔΩ =0.3a
3
/2. Using again K
e
for the
shear modulus, the maximum flow stress contribution is only σ
max
=8.6MPa.
With a characteristic dislocation density of
m
=2× 10
13
m
−2
, the diffusion
coefficient D necessary to obtain the flow stress maximum at the specific
temperature T
max
= 550
◦
C and strain rate ˙ε
max
=10
−5
s
−1
turns out to be
D =10
−19
m
2
s
−1
. This is exactly the diffusion coefficient of Fe at 550
◦
C
[609]. Thus, the Cottrell effect model of dynamic strain ageing can qualita-
tively interpret the dynamic deformation properties. It is consistent with the
366 9 Intermetallic Alloys
diffusion coefficient of Fe vacancies, but it fails to describe the amount of the
anomalous flow stress increase.
Dynamic strain ageing does also not explain the straight crystallographic
shape of the dislocations moving during the in situ experiments (Fig. 9.30
and Video 9.13). In general, the straight appearance of the dislocations can
be explained by the Peierls mechanism. However, it was shown above that
the Peierls mechanism is no more important at room temperature. Never-
theless, the straight arrangement of the moving dislocations is obviously a
property of the dislocation cores. There exist only a few theoretical studies
of the dislocation core configurations in FeAl (e.g., [610, 611]). They suggest
that dislocations with both 111 and 100 Burgers vectors dissociate into
partial dislocations with Burgers vectors close to 1/2111 which, however,
slightly point out of the {110} slip plane. Thus, these dislocations cannot
move conservatively in the dissociated configuration. The critical stresses to
move the dislocations on {110} planes at zero temperature are between 8 and
320 MPa. They are very different for screw and edge dislocations, but it seems
that these values are not relevant for the dislocation motion in the range of
the flow stress anomaly.
It is suggested in [8] to explain the straight crystallographically oriented
shape of dislocations by a decomposition model similar to that for the motion
of dislocations with 110 Burgers vectors during deformation of NiAl single
crystals in the hard 100 orientation described in Sect. 9.4.4. The proposed
model is fundamentally different from the climb dissociation model [584],
which was applied to FeAl in [596]. In FeAl, almost all preferential orien-
tations of the dislocations during motion are of the type 111, i.e., of the
screw orientation and a mixed orientation for dislocations with 111 Burgers
vectors as well as of a mixed orientation for the 100 dislocations. Only the
case of the 111 screw dislocation was treated in the core structure calcula-
tions in [610, 611]. Possible decomposition schemes in analogy to the model
for NiAl are listed in Table 9.4. According to that, the screw dislocation on
a (101) plane with a [11
¯
1] Burgers vector can decompose by glide into three
components with complete 100 Burgers vectors
[11
¯
1](101) → [100](0
¯
1
¯
1) + [010](101) + [00
¯
1](
¯
110) (9.7)
(reaction 1 in Table 9.4). All the slip planes involved are of the type {
110},
which seems to be the preferred slip plane in FeAl. The slip plane of the second
component is the same as that of the total dislocation so that this component
can move by glide. The two other components have to move by combined
glide and conservative climb as discussed for NiAl. Table 9.4 lists also the
character φ of all dislocations. The prelogarithmic factors of the energy E
0t
of the starting dislocation and those of the components E
0c
on the respective
slip planes were calculated again within the framework of anisotropic elasticity
theory as in Table 9.3. The last column of Table 9.4 contains the energy gain
E
0t
−
E
0c
by the reactions. It is strongly negative for the considered reaction
1 (9.7) so that this reaction is not driven by the elastic energy. Nevertheless, it

9.5 FeAl 367
Table 9.4. Suggested decomposition of dislocations with [11
¯
1] Burgers vectors on
(101) planes in FeAl
Reaction 1 2
Total disl.
line orient. [11
¯
1] [
¯
111]
φ 0
◦
109.5
◦
E
0t
(10
−9
N) 1.005 2.039
Comp. disls.
BV [100] [010] [00
¯
1] [100] [010] [00
¯
1]
Plane (0
¯
1
¯
1) (101) (
¯
101) (01
¯
1) (101) (110)
φ 54.7
◦
54.7
◦
54.7
◦
125.3
◦
54.7
◦
125.3
◦
E
0c
(10
−9
N) 0.593 0.593 0.593 0.593 0.593 0.593
Energy gain (10
−9
N) −0.774 0.26
may occur owing to a special core configuration although this reaction is not
suggested by the calculations in [610,611]. On the other hand, the near-edge
dislocation with a [11
¯
1] Burgers vector with a very high energy can decompose
with a considerable gain in elastic energy (reaction 2 in Table 9.4).
In the original model for NiAl [571], a dependence of the decomposition
width d on the deformation parameters is not explicitly considered. This leads
to a monotonously increasing dislocation mobility with increasing tempera-
ture. It is now suggested to extend the model by taking into account a possible
dependence of the width of the decomposed dislocations on the dislocation
velocity and the temperature. Since no detailed theory of this process is yet
available, it is assumed that the decomposition width plays a role similar to
the width of the diffusing point defect cloud around the dislocations in the
theory of the Cottrell effect described in Sect. 4.11. This dependence results
in the dynamic dislocation behavior of Fig. 4.39, leading to the occurrence of
a flow stress anomaly, the inverse dependence of the strain rate sensitivity
on the stain rate or stress, and to plastic instabilities, phenomena which are
all observed in the present material. Since both processes, the Cottrell effect
and the conservative climb motion of a decomposed dislocation require dif-
fusion processes in the dislocation cores over similar distances, (4.99) should
give a reasonable estimation of the temperature of the flow stress anomaly.
Climb in the dislocation cores in FeAl is quite probable since general climb
was observed in the same temperature range.
High-Temperature Range
The transition from the range of the flow stress anomaly to the high-
temperature range with a strongly decreasing flow stress may be caused by
two processes. As first suggested in [587], the dominating Burgers vectors
change from 111 to 100. A comparison between Videos 9.13 and 9.14 from
in situ straining experiments had shown that dislocations with 100 Burgers
368 9 Intermetallic Alloys
vectors are much more mobile than those with 111ones. In addition, recovery
processes become important.
In the in situ straining experiments, there is no indication of dislocations
with 100 Burgers vectors being formed by the decomposition of dislocations
with 111 Burgers vectors. Instead, the 100 dislocations moved in locally
separated bands and were generated within these bands by multiplication.
During their motion, the 100 dislocations are also straight and oriented
along 111 directions (Fig. 9.31), which may partly be due to the line tension.
However, the straight shape can also result from dissociation reactions, which
are not discussed in detail.
As demonstrated by Video 9.15 taken at 700
◦
C in the high-temperature
range, irregular dislocation motion points at rapid climb as a mode of dislo-
cation movement which also causes very fast recovery so that the dislocation
density during in situ straining remains on a low level. As the work-hardening
is low, the high-temperature deformation can conveniently be treated in terms
of an equation for steady state creep (5.20), as suggested in [593]. Depend-
ing on the particular creep model, stress exponents are expected between
about 4 and 6. Experimental stress exponents m
determined from the strain
rate sensitivity r according to (4.12) are equal to about 5 in the whole high-
temperature range. These experimental values fit the range of the theoretical
values for steady state creep. Thus, the strain rate sensitivity data also suggest
the importance of recovery during the high-temperature flow stress decrease.
9.5.4 Summary
Between room temperature and the temperature of the maximum of the
flow stress anomaly, Fe-43at%Al single crystals in a single slip orientation
are deformed by dislocations with 111 Burgers vectors. At room tempera-
ture, the dislocations bow out most probably between localized obstacles. The
flow stress anomaly is accompanied with an inverse dependence of the strain
rate sensitivity of the flow stress on the strain rate or the stress in a narrow
temperature range and with serrated flow. Curved slip traces during in situ
straining experiments in an HVEM and a nonplanar arrangement of disloca-
tions after macroscopic deformation indicate the importance of climb in the
range of the flow stress anomaly. In the in situ experiments, viscously moving
dislocations are straight and crystallographically oriented. These phenomena
are interpreted by a decomposition of the cores of the dislocations with 111
Burgers vectors into three component dislocations with 100 Burgers vectors
where, similar to the model for NiAl described in Sect. 9.4.4, two of the com-
ponent dislocations have to move by combined glide and conservative climb.
This model can be extended by considering a dependence of the decomposition
width on the temperature and the dislocation velocity resulting in a dynamic
behavior like the Cottrell effect and causing dynamic strain ageing. Above
the peak temperature, dislocations with 100 Burgers vectors dominate. The

9.6 Molybdenum Disilicide 369
deformation includes general climb and can be described by an equation for
steady state creep.
9.6 Molybdenum Disilicide
Materials based on molybdenum disilicide with its high melting point of
2,030
◦
C are promising for structural applications at high temperatures because
of their relatively high flow stress and good oxidation resistance above 1,000
◦
C
[612]. However, like other high-temperature materials MoSi
2
is very brittle at
room temperature and suffers from a low creep resistance at temperatures
of ductility. It has the tetragonal C11
b
structure with a high c/a ratio. This
implies strong plastic anisotropy. In the first studies on single crystals, a num-
ber of slip systems were observed, but plastic deformation was achieved only
above 900
◦
C [613–616]. Some of the slip systems have zero orientation fac-
tors for loading along [001] so that this orientation is a hard orientation. In
a thorough study of the orientation dependence of the plastic properties, it
was found that MoSi
2
can be deformed plastically even down to room tem-
perature, and lower, along orientations away from [001] [617]. In these soft
orientations, a flow stress anomaly occurs in different ranges between about
600 and 1,100
◦
C, depending on the orientation. The temperature dependence
of the critical resolved shear stress of most of the slip systems was gained
from macroscopic deformation data and from studies of the slip lines on the
surfaces and from the transmission electron microscope determination of the
Burgers vectors.
9.6.1 Crystal Structure and Slip Geometry
As mentioned above, stoichiometric MoSi
2
has the C11
b
structure up to
the melting point with an axial ratio c/a of almost exactly
√
6asshown
in Fig. 9.36. The structure consists of three b.c.c. cells, which are slightly
compressed and stacked along the c axis. This results in a pseudo-hexagonal
symmetry of the { 110} planes with almost identical lengths of the vectors
110 and 1/2111 as well as 1/2331 and 001. However, crystallographi-
cally, these directions are not equivalent as demonstrated in Fig. 9.37, which
shows the arrangement of two neighboring layers of atoms on the (110)
plane by black and grey circles. Among numerous slip systems possible,
{110}1/2111, { 011}100, {010}100, {110}1/2331, {013}1/2331,and
{011}1/2111 were experimentally proved [613–616]. The first four systems
have zero orientation factors for loading along [001]. The latter two have high
flow stresses, which makes [001] a hard orientation. The following experimen-
tal data are restricted to the soft (1
¯
10)1/2[111] and (011)[100] slip systems
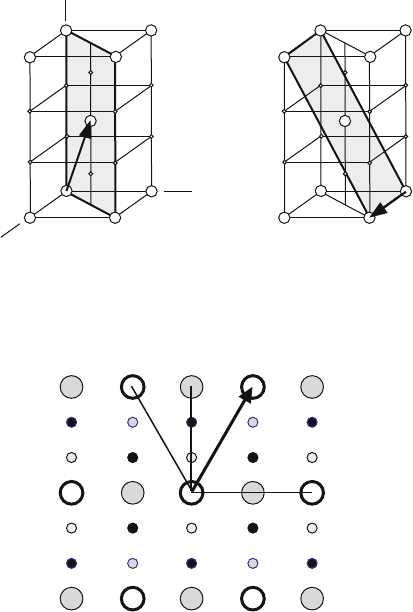
includedinFig.9.36aandb.
370 9 Intermetallic Alloys
[001]
[100]
[010]
Si
Mo
(a) (b)
Fig. 9.36. Crystal structure of MoSi
2
with (1
¯
10)1/2[111] (a) and (011)[100] slip
systems (b)
1/2[–1–11]
1/2[001]
1/2[111]
[110]
Si
Mo
Fig. 9.37. Structure of the (1
¯
10) slip plane in MoSi
2
with 1/2[111] Burgers vector.
Black circles are the atoms of the plane, grey ones those on the neighboring layers
9.6.2 Microscopic Observations
To activate the mentioned slip systems, MoSi
2
single crystals were deformed
along the [201] and [110] directions. The experimental data are collected from
[15,288,618–622].
Deformation Along 201
At this deformation axis, mainly dislocations with 1/2111 Burgers vec-
tors are activated. Figure 9.38a illustrates the dislocation structure from a
macroscopic deformation experiment at 300
◦
C. As will be shown in Sect. 9.6.3,
this temperature corresponds to the low-temperature decrease of the flow
stress. Under different imaging directions, most dislocations follow a straight
course. Via the contrast extinction rule (Sect. 2.3), their Burgers vector has

9.6 Molybdenum Disilicide 371
2µm
110
110
111
111
11-1
11-1
33-1
Fig. 9.38. Dislocation structures in MoSi
2
single crystals deformed along [201]
takeninanHVEM.(a) 300
◦
C, plastic strain 0.37%, beam direction n ≈ [1
¯
10]
perpendicular to (1
¯
10) slip plane, Burgers vector b [11
¯
1], g = (110). (b)atfirst
500
◦
C, then 850
◦
C, 1.5%, n ≈ [010], b [111], g = (200). Black bars mark the
indicated directions in the slip plane in (a) and their projections onto the image
plane in (b). From the work in [620]
been determined to be 1/2[11
¯
1]. The figure shows a view perpendicular to the
slip plane so that the line orientations can directly be determined. According
to that, the majority of dislocations is arranged parallel to [111]. Thus, they
are of 60
◦
character. In addition, also 30
◦
and edge dislocations occur. Very
few dislocations have 100 Burgers vectors.
In the temperature range of the flow stress anomaly, slip becomes localized
in narrow slip bands. The dislocations in Fig. 9.38b have 1/2[111] Burgers vec-
tors. They are mostly straight again in 60
◦
and edge orientation. However, in
contrast to the low-temperature range, the 60
◦
dislocations are now parallel to
[110]. As mentioned earlier and illustrated in Fig. 9.37, the 60
◦
directions par-
allel to 111 and 110 are crystallographically not equivalent. Thus, between
the low-temperature range and the anomaly range, the dominating line ori-
entation of straight 60
◦
dislocations with 1/2111 Burgers vectors exhibits a
transition from 111 to 110.
At temperatures between about 900 and 1,000
◦
C, a few in situ strain-
ing experiments in the HVEM were successful with deformation along [201]
demonstrating the dynamic dislocation behavior in the anomaly range. Similar
to γ-TiAl, dislocations are generated suddenly during elastic loading con-
nected with load drops LD demonstrated in the load time diagram of an in
situ straining experiment in Fig. 9.39. As in macroscopic experiments, slip is
concentrated in narrow slip bands. In all cases analyzed, the dislocations had
1/2111 Burgers vectors and were moving on {110} planes. Since these dislo-
cations were formed during the sudden load drops, they must have moved at
