Меньков А.В., Острейковский В.А. Теоретические основы автоматизированного управления
Подождите немного. Документ загружается.

140
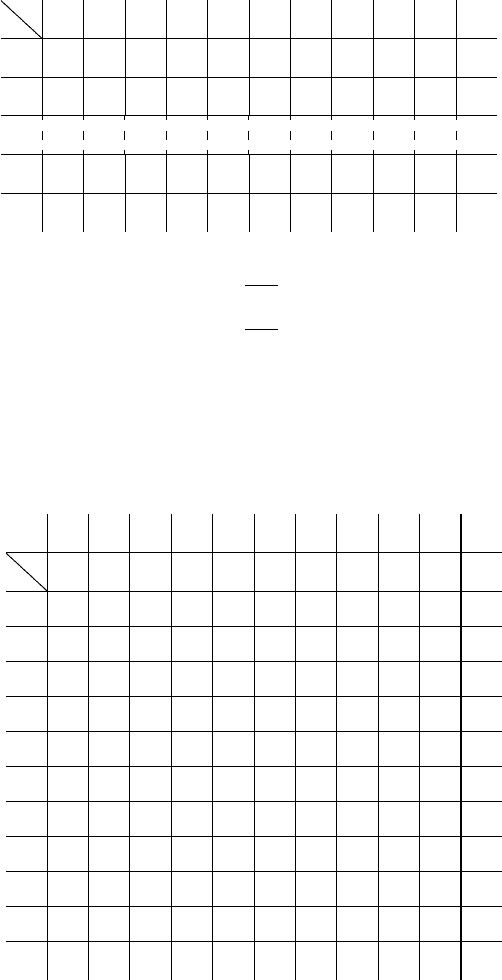
Оончательно имеем (табл. 4.16):
Таблица 4.16
Определим матриц A
3
: A
2
· A
и т. д.
12345678910σ
i
11113
2 12115
311
4 1113
A
2
= 5 1 1 2
60
70
80
90
10 0
σ
j
0000001534
a
1
(λ = 2) = 0
1
0
2
0
3
0
4
0
5
0
6
1
7
1
8
0
9
1
10
a
7
(λ = 1) = 0000000110
a
8
(λ = 1) = 0000000000
a
10
(λ = 1) = 0000000000
a
1
(λ = 3) =
0000000110
a
2
(λ = 2) = 0
1
0
2
0
3
0
4
0
5
0
6
1
7
2
8
1
9
1
10
a
7
(λ = 1) = 0000000110
2a
8
(λ = 1) 0000000000
a
10
(λ = 1) = 0000000000
a
2
(λ = 3) =
0000000110
j
i
141
Оончательно имеем:
Таблица 4 .1 7
Матрица A
4
= 0.
Находим σ
j
(λ) λ =
и σ
j
(λ) λ = .
Определяем матриц достижимости A(Σ): A(Σ) =
(табл. 4.18).
Таблица 4.18
12345678910σ
i
1112
A
3
= 2 1 1 2
1000000000000
σ
j
00000022000
12345678910σ
i
1 1 1311
2 1 2321
3111
4 11111
A(Σ) =5 1211
61
711
8
9
10
σ
j
0000001534
j
i
1 N,
1 N,
A
λ
λ 1=
N
∑
j
i
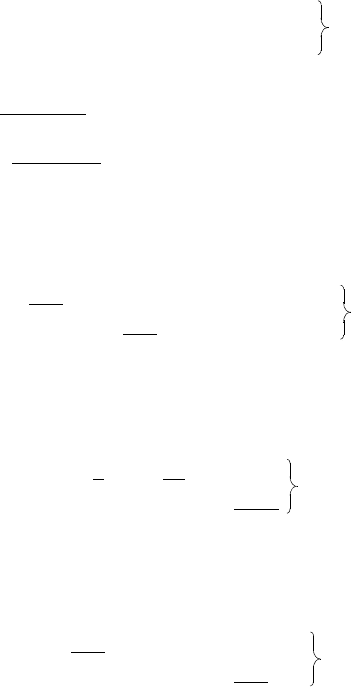
142
Последовательность вычисленных матриц позволяет фор-
мально определить все свойства анализиремо о информацион-
но о потоа.
Рассмотрим эти свойства в той же последовательности, в о-
торой они изла ались в теории.
1. Определение поряда элементов.
Для это о использется система
Определяем элементы нлево о поряда, для че о пола аем π
j
.
σ
j
(λ = 0) > 0 для j = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, та а любая
матрица в степени 0 дает 1.
σ
j
(λ = 1) = 0 для j = 1, 2, 3, 4 — это следет из матрицы A.
Совместно азанное соотношение выполняется для j = 1, 2, 3, 4.
Следовательно элементы X
1
, X
2
, X
3
, X
4
есть элементы нлево о
поряда.
Определеям элементы 1- о поряда, пола ая π
j
= 1.
Совместно заданные словия выполняются для j = 5, 6. Сле-
довательно, X
5
, X
6
— элементы перво о поряда.
Определяем элементы 2- о поряда, пола ая π
j
= 2.
Совместно заданные словия выполняются для j = 7, 10. Сле-
довательно, X
7
, X
10
– элементы второ о поряда.
Пола аем π
j
= 3.
Совместно заданные словия выполняются для j = 8, 9. Сле-
довательно, X
8
, X
9
— элементы третье о поряда.
2. Определение «татности» системы.
N = π
j
= 3.
Данная схема является трехтатной.
σ
j
(λ = π
j
+ 1) = 0.
σ
i
(λ = π
j
) = 0;
σ
j
(λ = 2) = 0 для j = 1, 2, 3, 4, 5, 6 (из матрицы А
2
).
σ
i
(λ = 1) > 0 для j = 5, 6, 7, 8, 9, 10 (из матрицы А
1
);
σ
j
(λ = 3) = 0 для j = 1, 2, 3, 4, 5, 6, 7, 10.
σ
i
(λ = 2) > 0 для j = 7, 8, 9, 10;
σ
j
(λ = 4) = 0 для j = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
σ
i
(λ = 3) > 0 для j = 8, 9;
max
j
143
3. Отстствие ненлевых элементов на лавной диаонали лю-
бой из матриц свидетельствет о том, что в анализиремом до-
ментообороте онтров нет.
4. Определение входных элементов потоа.
σ
j
(λ = 1) = 0 для j = 1, 2, 3, 4. Следовательно, элементы X
1
, X
2
,
X
3
, X
4
— входные элементы.
Например, σ
6
(λ = 1) = 2. Это означает, что в X
6
входят два эле-
мента, и т. д.
5. Определение выходных элементов потоа.
σ
i
(λ = 1) = 0 для i = 8, 9, 10. Следовательно, элементы X
8
, X
9
,
X
10
— выходные элементы.
Например, σ
5
(λ = 1) = 3. Это означает, что X
5
использется
для формирования 3-х др их элементов.
6. Определение висящих вершин.
Ситация σ
j
(λ = l) = σ
i
(λ = 1) = 0 отстствет, т.е. висящих
вершин нет.
7. Определение числа птей длиной λ.
Например, a
28
(λ = 2) = 2. Это означает, что от X
2
X
8
имеются
два различных пти длиною два.
8. Определение всевозможных птей межд двмя элементами.
Например, a
18
(Σ) = 3. Это означает, что от X
1
X
8
имеются три
различных пти длиною l.
9. Определение всех элементов, частвющих в формировании
данноо.
Например, отличные от нля элементы 8- о столбца матрицы
A(Σ) азывают все элементы потоа, частвющие в формирова-
нии X
8
, т. е. X
1
, X
2
, X
3
, X
4
, X
5
, X
7
, причем, например, X
5
– дважды;
а, например, ненлевые элементы 5-й строи матрицы A(Σ) а-
зывают все элементы, при формировании оторых использется
X
5
, т. е. X
7
, X
8
, X
9
, X
10
, причем для формирования X
8
элемент X
5
использется дважды.
10. Определение номера тата, после отороо данный элемент
может быть «поашен» в памяти системы.
Например, X
1
же не использется после τ
1
= 3, та а, сдя
по А, для формирования X
1
использется X
5
с τ
5
= 1 и X
8
с τ
8
= 3.
Масимм равен 3.
11. Определение числа татов хранения.
Например, для X
1
t
1
= τ
1
– π
1
= 3 – 0 = 3.
12. Рассмотрим столбцы матрицы A(В), соответствющие вы-
ходным элементам.
Например, столбец, соответствющий X
8
. Ка азывалось,
эта матрица задает число всех связей межд элементами. В фор-
142
Последовательность вычисленных матриц позволяет фор-
мально определить все свойства анализиремо о информацион-
но о потоа.
Рассмотрим эти свойства в той же последовательности, в о-
торой они изла ались в теории.
1. Определение поряда элементов.
Для это о использется система
Определяем элементы нлево о поряда, для че о пола аем π
j
.
σ
j
(λ = 0) > 0 для j = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, та а любая
матрица в степени 0 дает 1.
σ
j
(λ = 1) = 0 для j = 1, 2, 3, 4 — это следет из матрицы A.
Совместно азанное соотношение выполняется для j = 1, 2, 3, 4.
Следовательно элементы X
1
, X
2
, X
3
, X
4
есть элементы нлево о
поряда.
Определеям элементы 1- о поряда, пола ая π
j
= 1.
Совместно заданные словия выполняются для j = 5, 6. Сле-
довательно, X
5
, X
6
— элементы перво о поряда.
Определяем элементы 2- о поряда, пола ая π
j
= 2.
Совместно заданные словия выполняются для j = 7, 10. Сле-
довательно, X
7
, X
10
– элементы второ о поряда.
Пола аем π
j
= 3.
Совместно заданные словия выполняются для j = 8, 9. Сле-
довательно, X
8
, X
9
— элементы третье о поряда.
2. Определение «татности» системы.
N = π
j
= 3.
Данная схема является трехтатной.
σ
j
(λ = π
j
+ 1) = 0.
σ
i
(λ = π
j
) = 0;
σ
j
(λ = 2) = 0 для j = 1, 2, 3, 4, 5, 6 (из матрицы А
2
).
σ
i
(λ = 1) > 0 для j = 5, 6, 7, 8, 9, 10 (из матрицы А
1
);
σ
j
(λ = 3) = 0 для j = 1, 2, 3, 4, 5, 6, 7, 10.
σ
i
(λ = 2) > 0 для j = 7, 8, 9, 10;
σ
j
(λ = 4) = 0 для j = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
σ
i
(λ = 3) > 0 для j = 8, 9;
max
j
143
3. Отстствие ненлевых элементов на лавной диаонали лю-
бой из матриц свидетельствет о том, что в анализиремом до-
ментообороте онтров нет.
4. Определение входных элементов потоа.
σ
j
(λ = 1) = 0 для j = 1, 2, 3, 4. Следовательно, элементы X
1
, X
2
,
X
3
, X
4
— входные элементы.
Например, σ
6
(λ = 1) = 2. Это означает, что в X
6
входят два эле-
мента, и т. д.
5. Определение выходных элементов потоа.
σ
i
(λ = 1) = 0 для i = 8, 9, 10. Следовательно, элементы X
8
, X
9
,
X
10
— выходные элементы.
Например, σ
5
(λ = 1) = 3. Это означает, что X
5
использется
для формирования 3-х др их элементов.
6. Определение висящих вершин.
Ситация σ
j
(λ = l) = σ
i
(λ = 1) = 0 отстствет, т.е. висящих
вершин нет.
7. Определение числа птей длиной λ.
Например, a
28
(λ = 2) = 2. Это означает, что от X
2
X
8
имеются
два различных пти длиною два.
8. Определение всевозможных птей межд двмя элементами.
Например, a
18
(Σ) = 3. Это означает, что от X
1
X
8
имеются три
различных пти длиною l.
9. Определение всех элементов, частвющих в формировании
данноо.
Например, отличные от нля элементы 8- о столбца матрицы
A(Σ) азывают все элементы потоа, частвющие в формирова-
нии X
8
, т. е. X
1
, X
2
, X
3
, X
4
, X
5
, X
7
, причем, например, X
5
– дважды;
а, например, ненлевые элементы 5-й строи матрицы A(Σ) а-
зывают все элементы, при формировании оторых использется
X
5
, т. е. X
7
, X
8
, X
9
, X
10
, причем для формирования X
8
элемент X
5
использется дважды.
10. Определение номера тата, после отороо данный элемент
может быть «поашен» в памяти системы.
Например, X
1
же не использется после τ
1
= 3, та а, сдя
по А, для формирования X
1
использется X
5
с τ
5
= 1 и X
8
с τ
8
= 3.
Масимм равен 3.
11. Определение числа татов хранения.
Например, для X
1
t
1
= τ
1
– π
1
= 3 – 0 = 3.
12. Рассмотрим столбцы матрицы A(В), соответствющие вы-
ходным элементам.
Например, столбец, соответствющий X
8
. Ка азывалось,
эта матрица задает число всех связей межд элементами. В фор-
144
мировании X
8
частвют элементы
X
1
, X
2
, X
4
, X
5
и X
7
, причем X
1
и X
2
—
трижды, а X
5
— дважды.
Наличие большо о числа ненле-
вых и неединичных элементов в
столбце j = 8 свидетельствет о необ-
ходимости проведения содержатель-
но о анализа фра мента общей схе-
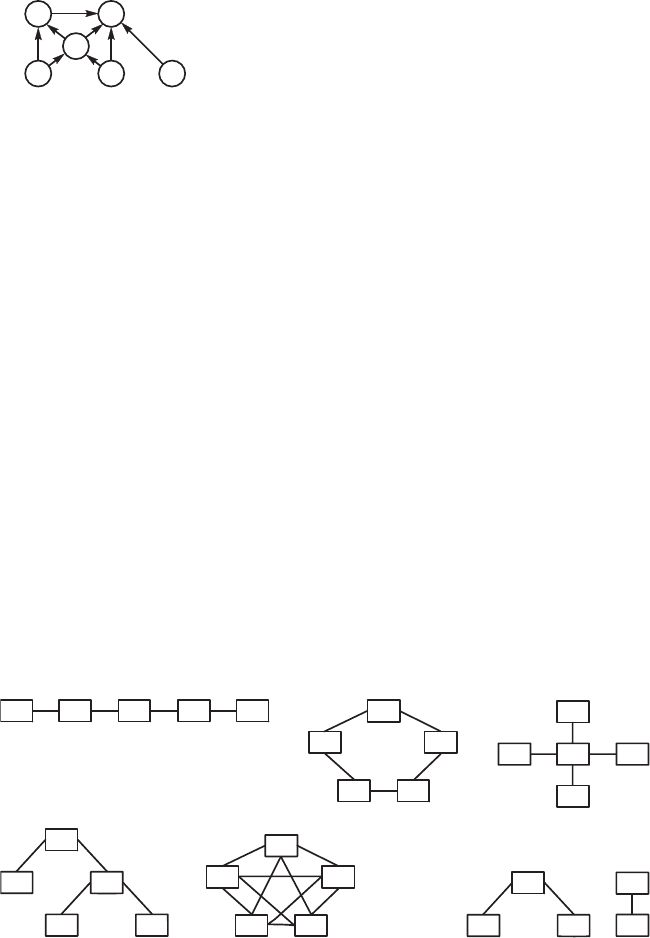
мы потоа, связанной с формированием X
8
(рис. 4.28). Быть мо-
жет, дастся простить фра мент за счет ислючения излишних
связей или промежточных элементов.
4.6. Стртрно-тополоичесие харатеристии
систем и их применение
При проведении анализа системы целесообразно оценить
оличественно ачество стртры системы и ее элементов
с позиций общесистемно о подхода. Рассмотрим основные
стртрно-тополо ичесие харатеристии. Сначала выделим
основные виды стртр с точи зрения тополо ии внтренних
связей.
Виды тополоичесих стртр. Виды тополо ичесих стр-
тр рассмотрим на примере пяти элементов.
Связность стртры. Данная харатеристиа позволяет выде-
лить наличие обрывов, висячие вершины и т. д. Для неориенти-
7
2 4
5
1
8
Рис. 4.28. Вид фра,-
мента ,рафа, связанно,о
с формированием X
8
.
1
1
2
2
3
51
4
2
3
4
43
5
5
3
1
2
54
3
1
2
1
2
43
5
4
5
á) â)
ã
)ä)
à)
å)
Рис. 4.29. Виды тополо,ичесих стртр: a) последовательная стртра;
б) ольцевая стртра; в) радиальная стртра; () древовидная стр-
тра; д) стртра типа полный (раф; e) несвязная стртра
145
рованных рафов связность всех элементов в стртре соответс-
твет выполнению словия:
0,5 = l n – 1, i ≠ j. (4.6)
В соотношении (4.6) a
ij
— элемент матрицы смежности. Пра-
вая часть (4.6) определяет необходимое минимальное число свя-
зей в стртре неориентированно о рафа, содержаще о n вер-
шин. Коэффициент 0,5 берется в сил то о, что одна и та же связь
a
i
и a
j
читывается дважды.
Соотношение (4.6) можно переписать в виде
0,5 = = m,
т.е. это не что иное, а число ребер в неориентированном рафе.
Определим m а фнцию от n для основных типов стртр
в общем виде.
Последовательная стртра. Очевидно m = n – 1.
Кольцевая стртра. Очевидно m = n.
Радиальная стртра. Очевидно m = n – 1.
Древовидная стртра. Трдно сазать в общем виде, та а
параметр определяется видом дерева.
Cтртра полный раф. Для перво о элемента число связей
n – 1, та а он связан со всеми элементами, роме себя.
У второ о элемента n – 2 связей, т.. нет связи с самим собой,
и связь с первым мы же чли. Анало ично третье о – n – 3
ит.д. Упоследне о – 0, та а все связи чтены. Ита, имеем
m =(n –1) + (n – 2) + (n – 3) + ... + 0 = 0,5n(n – 1).
Для несвязной стртры эта харатеристиа не имеет смысла.
Стртрная избыточность. Это стртрный параметр, отра-
жающий превышение обще о числа связей над необходимым ми-
нимальным числом связей. Разделим в соотношении (4.6) все
члены на n–1 и разность обозначим через R. То да бдем иметь
R = 0,5 – 1; (4.7)
R = , (4.8)
де R — стртрная избыточность.
a
ij
j 1=
n
∑
i 1=
n
∑
a
ij
j 1=
n
∑
i 1=
n
∑
a
ij
j 1=
n
∑
i 1=
n
∑
1
n 1−
------------
m
n 1−
------------
144
мировании X
8
частвют элементы
X
1
, X
2
, X
4
, X
5
и X
7
, причем X
1
и X
2
—
трижды, а X
5
— дважды.
Наличие большо о числа ненле-
вых и неединичных элементов в
столбце j = 8 свидетельствет о необ-
ходимости проведения содержатель-
но о анализа фра мента общей схе-
мы потоа, связанной с формированием X
8
(рис. 4.28). Быть мо-
жет, дастся простить фра мент за счет ислючения излишних
связей или промежточных элементов.
4.6. Стртрно-тополоичесие харатеристии
систем и их применение
При проведении анализа системы целесообразно оценить
оличественно ачество стртры системы и ее элементов
с позиций общесистемно о подхода. Рассмотрим основные
стртрно-тополо ичесие харатеристии. Сначала выделим
основные виды стртр с точи зрения тополо ии внтренних
связей.
Виды тополоичесих стртр. Виды тополо ичесих стр-
тр рассмотрим на примере пяти элементов.
Связность стртры. Данная харатеристиа позволяет выде-
лить наличие обрывов, висячие вершины и т. д. Для неориенти-
7
2 4
5
1
8
Рис. 4.28. Вид фра,-
мента ,рафа, связанно,о
с формированием X
8
.
1
1
2
2
3
51
4
2
3
4
43
5
5
3
1
2
54
3
1
2
1
2
43
5
4
5
á) â)
ã
)ä)
à)
å)
Рис. 4.29. Виды тополо,ичесих стртр: a) последовательная стртра;
б) ольцевая стртра; в) радиальная стртра; () древовидная стр-
тра; д) стртра типа полный (раф; e) несвязная стртра
145
рованных рафов связность всех элементов в стртре соответс-
твет выполнению словия:
0,5 = l n – 1, i ≠ j. (4.6)
В соотношении (4.6) a
ij
— элемент матрицы смежности. Пра-
вая часть (4.6) определяет необходимое минимальное число свя-
зей в стртре неориентированно о рафа, содержаще о n вер-
шин. Коэффициент 0,5 берется в сил то о, что одна и та же связь
a
i
и a
j
читывается дважды.
Соотношение (4.6) можно переписать в виде
0,5 = = m,
т.е. это не что иное, а число ребер в неориентированном рафе.
Определим m а фнцию от n для основных типов стртр
в общем виде.
Последовательная стртра. Очевидно m = n – 1.
Кольцевая стртра. Очевидно m = n.
Радиальная стртра. Очевидно m = n – 1.
Древовидная стртра. Трдно сазать в общем виде, та а
параметр определяется видом дерева.
Cтртра полный раф. Для перво о элемента число связей
n – 1, та а он связан со всеми элементами, роме себя.
У второ о элемента n – 2 связей, т.. нет связи с самим собой,
и связь с первым мы же чли. Анало ично третье о – n – 3
ит.д. Упоследне о – 0, та а все связи чтены. Ита, имеем
m =(n –1) + (n – 2) + (n – 3) + ... + 0 = 0,5n(n – 1).
Для несвязной стртры эта харатеристиа не имеет смысла.
Стртрная избыточность. Это стртрный параметр, отра-
жающий превышение обще о числа связей над необходимым ми-
нимальным числом связей. Разделим в соотношении (4.6) все
члены на n–1 и разность обозначим через R. То да бдем иметь
R = 0,5 – 1; (4.7)
R = , (4.8)
де R — стртрная избыточность.
a
ij
j 1=
n
∑
i 1=
n
∑
a
ij
j 1=
n
∑
i 1=
n
∑
a
ij
j 1=
n
∑
i 1=
n
∑
1
n 1−
------------
m
n 1−
------------
146
Найдем стртрню избыточность для рассмотренных типо-
вых стртр в общем виде, читывая ранее найденню зависи-
мость m = m(n).
1. Последовательная стртра: m = n – 1; R = –1 = 0.
2. Кольцевая стртра: m = n; R = –1 = .
3. Радиальная стртра: m = n – 1; R = –1 = 0.
4. Стртра полный раф: m = ; R = –1 = .
Данная стртрная харатеристиа использется для освен-
ной оцени эономичности и надежности исследемой системы.
Для систем с избыточностью — R > 0, для систем с минимальной
избыточностью – R = 0, для несвязных систем – R < 0.
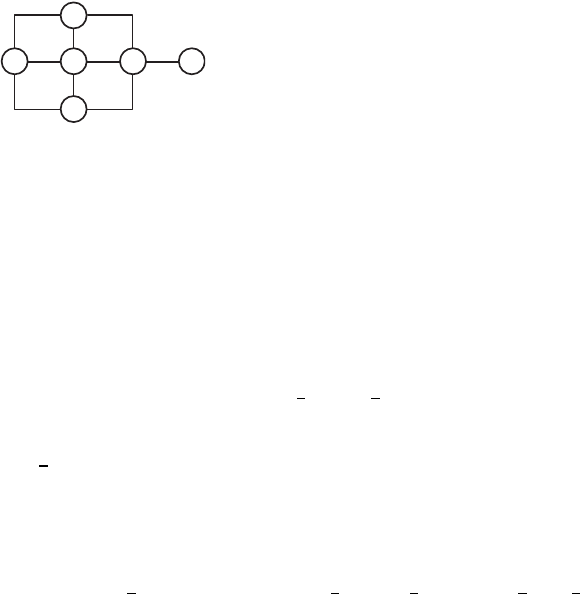
Очевидно, что чем больше R, тем
потенциально более надежна систе-
ма, но стртрная избыточность мо-
жет быть дости нта за счет величе-
ния связности тольо одних вершин
(см. рис. 4.30).
Поэтом вводят параметр ε
2
, читы-
вающий неравномерность распределе-
ния связей или их несимметричность.
Вспомним понятие «степень вершины» ρ
i
, т. е. число ребер,
инцидентных вершине i. Было поазано, что
0,5 = m.
Если связи распределены равномерно, то, очевидно, все с
i
одинаовы. То да
= и = 2 ,
де — средняя степень вершины.
Теперь можно определить вадратичные отлонения распре-
деления степеней вершин от равномерно о.
Средневадратичное отлонение равно
= = – 2 + ; 2 = 2 .
n 1−
n 1−
------------
n
n 1−
------------
1
n 1−
------------
n 1−
n 1−
------------
nn 1−()
2
--------------------
nn 1−()
2 n 1−()
--------------------
n 2−
2
------------
Рис. 4.30. Вид ,рафа
⎝
⎛
ρ
i
i 1=
n
∑
⎠
⎞
ρ
i
i 1=
n
∑
nρ ρ
m
n
----
ρ
ε
2
ρ
i
ρ−()
2
i 1=
n
∑
ρ
i
2
i 1=
n
∑
ρ
i
ρ
i 1=
n
∑
ρ()
2
i 1=
n
∑
ρ
i
ρ
i 1=
n
∑
ρ ρ
i
i 1=
n
∑
147
Та а = 2m и = 2 , то 2 = 2 · 2 · n · 2 =
= 8 ; 2 = 4 · n = .
И, оончательно,
ε
2
= – 8 + 4 ;
ε
2
= – . (4.9)
Поазатель ε
2
харатеризет недоиспользованные возмож-
ности заданной стртры, имеющей m ребер и n вершин.
Рассмотрим стртрню неравномерность для типовых схем.
1. Последовательная стртра:
m = n – 1. То да = .
= 1
2
+ + 1
2
= 2 + 2
2
(n – 2) = 4n – 6.
ε
2
= 4n – 6 – = .
2. Кольцевая стртра:
m = n, = = 2
2
n.
ε
2
= 2
2
n – = 0.
3. Радиальная стртра:
m = n – 1, = (n – 1)
2
+ = n(n – 1).
ε
2
= n(n – 1) – = .
ρ
i
i 1=
n
∑
ρ
m
n
----
ρ
i
ρ
i 1=
n
∑
ρ
m
n
----
m
n
----
m
2
n
------
ρ
2
i 1=
n
∑
m
2
n
2
------
4m
2
n
----------
ρ
i
2
i 1=
n
∑
m
2
n
------
m
2
n
------
ρ
i
2
i 1=
n
∑
4m
2
n
----------
4m
2
n
----------
4 n 1−()
2
n
---------------------- -
ρ
i
2
i 1=
n
∑
2
2
+ 2
2
+ ... + 2
2
n – 2
4 n 2−()
2
n
---------------------- -
2 n 2−()
n
--------------------
ρ
i
2
i 1=
n
∑
2
2
+ 2
2
+ ... + 2
2
n
4n
2
n
--------
ρ
i
2
i 1=
n
∑
1
2
+ 1
2
+ ... + 1
2
n – 1
4 n 1−()
2
n
---------------------- -
n 1−()n 2−()
2
n
-------------------------------------

146
Найдем стртрню избыточность для рассмотренных типо-
вых стртр в общем виде, читывая ранее найденню зависи-
мость m = m(n).
1. Последовательная стртра: m = n – 1; R = –1 = 0.
2. Кольцевая стртра: m = n; R = –1 = .
3. Радиальная стртра: m = n – 1; R = –1 = 0.
4. Стртра полный раф: m = ; R = –1 = .
Данная стртрная харатеристиа использется для освен-
ной оцени эономичности и надежности исследемой системы.
Для систем с избыточностью — R > 0, для систем с минимальной
избыточностью – R = 0, для несвязных систем – R < 0.
Очевидно, что чем больше R, тем
потенциально более надежна систе-
ма, но стртрная избыточность мо-
жет быть дости нта за счет величе-
ния связности тольо одних вершин
(см. рис. 4.30).
Поэтом вводят параметр ε
2
, читы-
вающий неравномерность распределе-
ния связей или их несимметричность.
Вспомним понятие «степень вершины» ρ
i
, т. е. число ребер,
инцидентных вершине i. Было поазано, что
0,5 = m.
Если связи распределены равномерно, то, очевидно, все с
i
одинаовы. То да
= и = 2 ,
де — средняя степень вершины.
Теперь можно определить вадратичные отлонения распре-
деления степеней вершин от равномерно о.
Средневадратичное отлонение равно
= = – 2 + ; 2 = 2 .
n 1−
n 1−
------------
n
n 1−
------------
1
n 1−
------------
n 1−
n 1−
------------
nn 1−()
2
--------------------
nn 1−()
2 n 1−()
--------------------
n 2−
2
------------
Рис. 4.30. Вид ,рафа
⎝
⎛
ρ
i
i 1=
n
∑
⎠
⎞
ρ
i
i 1=
n
∑
nρ ρ
m
n
----
ρ
ε
2
ρ
i
ρ−()
2
i 1=
n
∑
ρ
i
2
i 1=
n
∑
ρ
i
ρ
i 1=
n
∑
ρ()
2
i 1=
n
∑
ρ
i
ρ
i 1=
n
∑
ρ ρ
i
i 1=
n
∑
147
Та а = 2m и = 2 , то 2 = 2 · 2 · n · 2 =
= 8 ; 2 = 4 · n = .
И, оончательно,
ε
2
= – 8 + 4 ;
ε
2
= – . (4.9)
Поазатель ε
2
харатеризет недоиспользованные возмож-
ности заданной стртры, имеющей m ребер и n вершин.
Рассмотрим стртрню неравномерность для типовых схем.
1. Последовательная стртра:
m = n – 1. То да = .
= 1
2
+ + 1
2
= 2 + 2
2
(n – 2) = 4n – 6.
ε
2
= 4n – 6 – = .
2. Кольцевая стртра:
m = n, = = 2
2
n.
ε
2
= 2
2
n – = 0.
3. Радиальная стртра:
m = n – 1, = (n – 1)
2
+ = n(n – 1).
ε
2
= n(n – 1) – = .
ρ
i
i 1=
n
∑
ρ
m
n
----
ρ
i
ρ
i 1=
n
∑
ρ
m
n
----
m
n
----
m
2
n
------
ρ
2
i 1=
n
∑
m
2
n
2
------
4m
2
n
----------
ρ
i
2
i 1=
n
∑
m
2
n
------
m
2
n
------
ρ
i
2
i 1=
n
∑
4m
2
n
----------
4m
2
n
----------
4 n 1−()
2
n
---------------------- -
ρ
i
2
i 1=
n
∑
2
2
+ 2
2
+ ... + 2
2
n – 2
4 n 2−()
2
n
---------------------- -
2 n 2−()
n
--------------------
ρ
i
2
i 1=
n
∑
2
2
+ 2
2
+ ... + 2
2
n
4n
2
n
--------
ρ
i
2
i 1=
n
∑
1
2
+ 1
2
+ ... + 1
2
n – 1
4 n 1−()
2
n
---------------------- -
n 1−()n 2−()
2
n
-------------------------------------
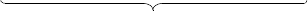
148
4. Стртра полный раф:
m = , = · = n(n – 1)
2
.
= = n(n – 1)
2
.
ε
2
= n(n – 1)
2
– n(n – 1)
2
= 0.
Стртрная омпатность. Для ее оцени вводится параметр,
отображающий близость элементов межд собой. Близость 2-х
элементов i и j определяется через минимальню длин пти для
ориентированно о рафа (цепи — для неориентированно о) — d
ij
.
То да смма всех минимальных птей (цепей) межд всеми эле-
ментами отражает общю стртрню близость элементов в ана-
лизиремой стртре. Обозначим эт величин через Q и, в со-
ответствии с определением, бдем иметь:
Q = , i ≠ j.(4.10)
Рассмотрим этот параметр для основных стртр.
1. Последовательная стртра.
Непосредственно из ее изображения имеем:
Для 1- о элемента
= d
12
+ d
13
+ d
14
+ d
15
+ ... + d
1n
= 1 + 2 + 3 + 4 + ... + n – 1.
Для 2- о элемента
= d
21
+ d
23
+ d
24
+ d
25
+ ... + d
2n
= 1 + 1 + 1 + 3 + ... + n – 2.
Для 3- о элемента
= d
31
+ d
33
+ d
34
+ d
35
+ ... + d
3n
= 2 + 1 + 1 + 2 + ... + n – 3.
Для n- о элемента
= n – 1 + ... + 4 + 3 + 2 + 1.
nn 1−()
2
--------------------
4m
2
n
----------
4
n
-- -
n
2
n 1−()
2
4
-------------------------
ρ
i
2
i 1=
n
∑
(n –1)
2
+ (n –1)
2
+ ... + (n –1)
2
n
d
ij
j 1=
n
∑
i 1=
n
∑
d
1j
j
1=
n
∑
d
2j
j
1=
n
∑
d
3j
j
1=
n
∑
d
nj
j
1=
n
∑
149
Перепишем это иначе:
Теперь очевидно, что Q
1
= Q
2
и Q = 2Q
1
.
Рассмотрим Q
1
. Смма натральных чисел по столбцам равна
Q
1
= 1(n – 1) + 2(n – 1 – 1) + 3(n – 1 – 1 – 1) + ... + (n – 1).
Q
1
= 1(n – 1) + 2(n – 2) + 3(n – 3) + ... + (n – 1).
Q
1
= .
И, оончательно,
Q = 2 . (4.11)
Расроем последнее выражение
Q = 2n – 2 .
Известна справочная формла
= .
Отда
2 = .
И, оончательно,
Q = n(n
2
– 1). (4.12)
Q
1
1 +
2 + 1 +
1 + 2 + 3 + 4 + ....... + (n – 1)
1 + 2 + 3 + 4 + ..... + (n – 2)
1 + 2 + 3 + 4 + ... + (n – 3)
(n – 1) + ....... + 4 + 3 + 2 + 1
(n – 2) + ..... + 4 + 3 + 2 + 1
(n – 3) + ... + 4 + 3 + 2 + 1
+ 1 Q
2
+ 1 + 2
n
–
1
n – 1
in i−()
i 1=
n 1−
∑
in i−()
i 1=
n
1
−
∑
i
i 1=
n
1
−
∑
i
2
i 1=
n 1−
∑
i
2
i 1=
n
∑
nn 1+()2n 1+()
6
-----------------------------------------
i
2
i 1=
n
∑
nn 1−()2n 1−()
3
-----------------------------------------
1
3
-- -
148
4. Стртра полный раф:
m = , = · = n(n – 1)
2
.
= = n(n – 1)
2
.
ε
2
= n(n – 1)
2
– n(n – 1)
2
= 0.
Стртрная омпатность. Для ее оцени вводится параметр,
отображающий близость элементов межд собой. Близость 2-х
элементов i и j определяется через минимальню длин пти для
ориентированно о рафа (цепи — для неориентированно о) — d
ij
.
То да смма всех минимальных птей (цепей) межд всеми эле-
ментами отражает общю стртрню близость элементов в ана-
лизиремой стртре. Обозначим эт величин через Q и, в со-
ответствии с определением, бдем иметь:
Q = , i ≠ j.(4.10)
Рассмотрим этот параметр для основных стртр.
1. Последовательная стртра.
Непосредственно из ее изображения имеем:
Для 1- о элемента
= d
12
+ d
13
+ d
14
+ d
15
+ ... + d
1n
= 1 + 2 + 3 + 4 + ... + n – 1.
Для 2- о элемента
= d
21
+ d
23
+ d
24
+ d
25
+ ... + d
2n
= 1 + 1 + 1 + 3 + ... + n – 2.
Для 3- о элемента
= d
31
+ d
33
+ d
34
+ d
35
+ ... + d
3n
= 2 + 1 + 1 + 2 + ... + n – 3.
Для n- о элемента
= n – 1 + ... + 4 + 3 + 2 + 1.
nn 1−()
2
--------------------
4m
2
n
----------
4
n
-- -
n
2
n 1−()
2
4
-------------------------
ρ
i
2
i 1=
n
∑
(n –1)
2
+ (n –1)
2
+ ... + (n –1)
2
n
d
ij
j 1=
n
∑
i 1=
n
∑
d
1j
j
1=
n
∑
d
2j
j
1=
n
∑
d
3j
j
1=
n
∑
d
nj
j
1=
n
∑
149
Перепишем это иначе:
Теперь очевидно, что Q
1
= Q
2
и Q = 2Q
1
.
Рассмотрим Q
1
. Смма натральных чисел по столбцам равна
Q
1
= 1(n – 1) + 2(n – 1 – 1) + 3(n – 1 – 1 – 1) + ... + (n – 1).
Q
1
= 1(n – 1) + 2(n – 2) + 3(n – 3) + ... + (n – 1).
Q
1
= .
И, оончательно,
Q = 2 . (4.11)
Расроем последнее выражение
Q = 2n – 2 .
Известна справочная формла
= .
Отда
2 = .
И, оончательно,
Q = n(n
2
– 1). (4.12)
Q
1
1 +
2 + 1 +
1 + 2 + 3 + 4 + ....... + (n – 1)
1 + 2 + 3 + 4 + ..... + (n – 2)
1 + 2 + 3 + 4 + ... + (n – 3)
(n – 1) + ....... + 4 + 3 + 2 + 1
(n – 2) + ..... + 4 + 3 + 2 + 1
(n – 3) + ... + 4 + 3 + 2 + 1
+ 1 Q
2
+ 1 + 2
n
–
1
n – 1
in i−()
i 1=
n 1−
∑
in i−()
i 1=
n
1
−
∑
i
i 1=
n
1
−
∑
i
2
i 1=
n 1−
∑
i
2
i 1=
n
∑
nn 1+()2n 1+()
6
-----------------------------------------
i
2
i 1=
n
∑
nn 1−()2n 1−()
3
-----------------------------------------
1
3
-- -
150
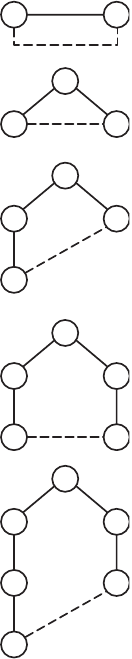
2. Кольцевая стртра. Имеем для 1- о элемента (i =1)
Теперь очевидно, что для n – нечетно о
= 1 + 2 + 3 + ... + + 1 + 2 + 3 + ... + ;
= 2 · 1 + = .
Мы нашли смм всех минимальных птей (цепей) для 1- о
элемента (в слчае нечетно о числа элементов). И это справедли-
во для всех n элементов.Оончательно (для n – нечетно о)
Q = . (4.13)
n = 2 d
12
= 1;
n = 3
= 1 + 1;
n = 4 = 1 + 2 + 1;
n = 5 = 1 + 2 + 1 + 2;
n = 6 = 1 + 2 + 3 + 1 + 2.
1 2
2
1
3
23
d
1j
j
1=
3
∑
4
2
1
3
23
d
1j
j
1=
4
∑
4 5
2
1
3
23
d
1j
j
1=
5
∑
3 6
4
2
1
5
2
d
1j
j
1=
6
∑
d
1j
j
1=
n
∑
n 1−
2
------------
n 1−
2
------------
d
1j
j
1=
n
∑
⎝
⎛
n 1−
2
------------
⎠
⎞
⎝
⎛
n 1−
4
------ ------
⎠
⎞
n
2
1−
4
--------------
nn
2
1+()
4
---------------------- -
151
Для n – четно о имеем
= 1 + 2 + 3 + ... + + 1 + 2 + 3 + ... + – = .
И, оончательно, для n – четно о
Q = . (4.14)
3. Радиальная стртра.
Непосредственно из ее изображения (см. п. 4.6.1) имеем для
центрально о элемента
= 1(n – 1).
Для второ о и, в сил симметричности, любо о из оставшихся
элементов, имее
м
= = ... = 1 + 2(n – 2) = 2n – 3.
Первый член в последнем выражении 1 – это пть до 1- о
элемента, второй 2 – для любо о др о о, а их (n – 2), та а нет
связи с самим собой, а связь с первым же чтена. И таих свя-
зей, очевидно, (n – 1). То да
Q = (n – 1) + (2n – 3)(n – 1);
Q = 2(n – 1)
2
.(4.15)
4. Стртра полный раф.
У аждо о элемента есть связи со всеми, роме себя. Это –
(n– 1), а все о вершин n. Ита, имеем
Q = n(n – 1).
Для оцени стртрной омпатности часто использется
относительный поазатель
Q
отн
= – 1, (4.16)
де Q
min
= n(n – 1) — минимальное значение омпатности для
стртры типа полный раф.
d
1j
j
1=
n
∑
n
2
-- -
n
2
-- -
n
2
-- -
n
2
4
-----
n
3
4
-----
j
1=
n
∑
d
2j
j
1=
n
∑
d
3j
j
1=
n
∑
Q
Q
min
------------
