Меньков А.В., Острейковский В.А. Теоретические основы автоматизированного управления
Подождите немного. Документ загружается.

160
2. Кольцевая стртра:
m = n; R = – 1 = = 0,1.
3. Радиальная стртра:
m = n – 1; R = – 1 = 0.
4. Древовидная стртра (в данном онретном слчае):
R = – 1 = – 1 = 0,33.
5. Стртра полный раф:
m = ; R – 1 = = 4.
Средневадратичное отлонение
ε
2
= – .
1. Последовательная стртра:
ε
2
= = 1,6.
2. Кольцевая стртра:
ε
2
=0.
3. Радиальная стртра:
ε
2
= = 57,6.
4. Древовидная стртра (в данном онретном слчае):
ε
2
= 2
2
+ 3
2
+ 3
2
+ 3
2
+ 2
2
+ 1
1
+ 3
2
+ 1
2
+
+ 1
2
+ 1
2
+ 1
2
+ 1
2
– = 7,6.
5. Стртра полный раф:
ε
2
= 0.
n
n 1−
------------
1
n 1−
------------
n
1
−
n 1−
------------
m
n 1−
------------
12
10 1−
---------------
nn 1−()
2
--------------------
nn 1−()
2 n 1−()
--------------------
n 2−
2
------------
ρ
i
2
i 1=
10
∑
4m
2
n
----------
2 n 2−()
n
--------------------
n 1−()n 2−()
2
2
-------------------------------------
49
2
⋅
10
------------ -
161
Стртрная омпатность
Q = , i ≠ j.
1. Последовательная стртра:
Q = n(n
2
– 1) = 330.
2. Кольцевая стртра:
Q = = 250.
3. Радиальная стртра:
Q = 2(n – 1)
2
= 162.
4. Древовидная стртра (в данном онретном слчае):
= 1 + 1 + 2 + 2 + 2 + 2 + 3 + 3 + 4 = 20,
Q = 20 + 17 + 23 + 21 + 25 + 31 + 31 + 29 + 29 + 31 = 257.
5. Стртра полный раф:
Q = n(n – 1) = 90.
Относительная стртрная омпатность
Q
отн
= – 1.
1. Последовательная стртра:
Q
отн
= – 1 = 2,67.
2. Кольцевая стртрa:
Q
отн
= – 1 = 1,78.
3. Радиальная стртра:
Q
отн
= – 1 = 0,8.
d
ij
j 1=
n
∑
i 1=
n
∑
1
3
-- -
n
3
4
-----
d
1j
i 1=
10
∑
Q
Q
min
------ ------
330
90
-------- -
250
90
-------- -
162
90
--------

162
4. Древовидная стртра (в данном онретном слчае):
Q
отн
= – 1 = 1,85.
5. Стртра полный раф:
Q
отн
= – 1 = 0.
Степень централизации
γ = , де 2z
max
= .
1. Последовательная стртра.
Можно поазать, что для N-но о элемента (т. е. элемента, на-
ходяще ося на месте N) справедливо соотношение
= + .
Для n = 10 и N = 5 и N = 6:
= = + =
= + = 25;
2z
max
= = 13,2;
γ = = 0,18.
2. Кольцевая стртрa:
2z
max
= n и γ = 0.
3. Радиальная стртра:
2z
max
= = 2(n – 1). γ = = 1.
257
90
-------- -
90
90
----- -
n 1−()2z
max
n−()
n 2−()z
max
--------------------------------------------- -
Q
d
ij
j 1=
n
∑
---------------------
d
ij
j
1=
n
∑
ii 1+()
2
-----------------
ni−()ni− 1−()
2
-----------------------------------------
d
5j
j
1=
10
∑
min
d
6j
j
1=
10
∑
min
44 1+()
2
--------------------
10 4−()10 4− 1−()
2
-------------------------------------------------
55 1+()
2
--------------------
10 5−()10 5− 1−()
2
-------------------------------------------------
330
25
-------- -
10 1−()2132 10−,()
10 2−()13 2,⋅
----------------------------------------------------
2 n 1−()
2
n 1−
---------------------- -
n 1−()2 n 1−()()n−
2 n 2−()n 1−()
----------------------------------------------------
163
4. Древовидная стртра (в данном онретном слчае):
2z
max
= =15,12. γ = = 0,76.
5. Стртра полный раф:
2z
max
= = n и γ = 0.
Ита, имеем:
Таблица 4 .1 7
Из табл. 4.17 cледет, что по своим параметрам анализиремая
стртра ближе все о древовидной стртре.
Если заранее изчить свойства типовых стртр, то можно с
большой степенью веренности сдить о свойствах анализире-
мой стртры по близости соответствющих параметров.
4.7. Модели фнционирования
оранизационной системы
Основные допщения и определения. Для построения матема-
тичесой модели стртрно о сопряжения элементов в системе
введем ряд допщений:
1. Входной си нал x(t), постпающий элемент в момент
времени t, бдем рассматривать а совопность элементарных
си налов x
1
(t), x
2
(t), …, x
m
(t), одновременно возниающих на
входах элемента.
R ε
2
QQ
отн
d γ
Последовательная 0 1,6 330 2,67 9 0,18
Кольцевая 0,1 0 250 1,78 2 0
Радиальная 0 57,6 162 0,8 2 1,0
Древовидная 0,33 7,6 257 1,85 5 0,76
Полный раф 4 0 90 0 1 0
Анализир. стрт. 0,33 10,4 210 1,3 5 0,643
257
17
-------- -
10 1−()15 12 10−,()2
10 2−()15 12,
-------------------------------------------------------
nn 1−()
n 1−
--------------------
Параметр
Стртра

162
4. Древовидная стртра (в данном онретном слчае):
Q
отн
= – 1 = 1,85.
5. Стртра полный раф:
Q
отн
= – 1 = 0.
Степень централизации
γ = , де 2z
max
= .
1. Последовательная стртра.
Можно поазать, что для N-но о элемента (т. е. элемента, на-
ходяще ося на месте N) справедливо соотношение
= + .
Для n = 10 и N = 5 и N = 6:
= = + =
= + = 25;
2z
max
= = 13,2;
γ = = 0,18.
2. Кольцевая стртрa:
2z
max
= n и γ = 0.
3. Радиальная стртра:
2z
max
= = 2(n – 1). γ = = 1.
257
90
-------- -
90
90
----- -
n 1−()2z
max
n−()
n 2−()z
max
--------------------------------------------- -
Q
d
ij
j 1=
n
∑
---------------------
d
ij
j
1=
n
∑
ii 1+()
2
-----------------
ni−()ni− 1−()
2
-----------------------------------------
d
5j
j
1=
10
∑
min
d
6j
j
1=
10
∑
min
44 1+()
2
--------------------
10 4−()10 4− 1−()
2
-------------------------------------------------
55 1+()
2
--------------------
10 5−()10 5− 1−()
2
-------------------------------------------------
330
25
-------- -
10 1−()2132 10−,()
10 2−()13 2,⋅
----------------------------------------------------
2 n 1−()
2
n 1−
---------------------- -
n 1−()2 n 1−()()n−
2 n 2−()n 1−()
----------------------------------------------------
163
4. Древовидная стртра (в данном онретном слчае):
2z
max
= =15,12. γ = = 0,76.
5. Стртра полный раф:
2z
max
= = n и γ = 0.
Ита, имеем:
Таблица 4 .1 7
Из табл. 4.17 cледет, что по своим параметрам анализиремая
стртра ближе все о древовидной стртре.
Если заранее изчить свойства типовых стртр, то можно с
большой степенью веренности сдить о свойствах анализире-
мой стртры по близости соответствющих параметров.
4.7. Модели фнционирования
оранизационной системы
Основные допщения и определения. Для построения матема-
тичесой модели стртрно о сопряжения элементов в системе
введем ряд допщений:
1. Входной си нал x(t), постпающий элемент в момент
времени t, бдем рассматривать а совопность элементарных
си налов x
1
(t), x
2
(t), …, x
m
(t), одновременно возниающих на
входах элемента.
R ε
2
QQ
отн
d γ
Последовательная 0 1,6 330 2,67 9 0,18
Кольцевая 0,1 0 250 1,78 2 0
Радиальная 0 57,6 162 0,8 2 1,0
Древовидная 0,33 7,6 257 1,85 5 0,76
Полный раф 4 0 90 0 1 0
Анализир. стрт. 0,33 10,4 210 1,3 5 0,643
257
17
-------- -
10 1−()15 12 10−,()2
10 2−()15 12,
-------------------------------------------------------
nn 1−()
n 1−
--------------------
Параметр
Стртра
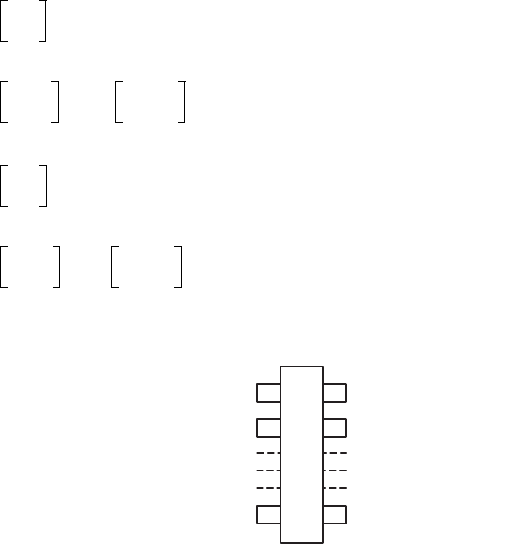
164
2. Выходной си нал y(t) анало ично может рассматриваться а
совопность элементарных выходных си налов y
1
(t), y
2
(t), …, y
n
(t).
3. Элементарные си налы передаются в системе независимо
др от др а по элементарным аналам.
4. К входном онтат любо о элемента может быть подлю-
чен не более чем один элементарный анал.
5. К выходном онтат любо о элемента может быть под-
лючено любое оличество элементарных аналов.
Ита, псть система S состоит из N элементов. Для i-то о эле-
мента, обозначим е о через C
i
, в соответствии с введенными до-
пщениями мы имеем:
= , , ..., — множество входных онтатов
элемента;
x
i
(t) ° (t) — множество входных си налов это о
элемента;
= , , ..., — множество выходных онта-
тов элемента;
y
i
(t) ° (t) — множество выходных си налов это о
элемента.
Графичеси это вы лядит следющим образом (рис. 4.31):
Взаимодействие системы с внешней средой рассматривается
а обмен си налами межд внешней средой и элементами сис-
темы, причем для всех этих си налов справедливы все отмечен-
ные выше допщения. В соответствии с этим внешнюю сред
можно представить в виде фитивно о элемента системы C
0
, при-
X
j
i
1
m
i
⎩
⎨
⎧
X
1
i
X
2
i
X
m
i
i
⎭
⎬
⎫
1
m
i
X
j
i
1
m
i
Y
j
i
1
n
i
⎩
⎨
⎧
Y
1
i
Y
2
i
Y
n
i
i
⎭
⎬
⎫
1
n
i
Y
j
i
1
n
i
]
1
X
j
i
(t)]
1
; [
m
i
[x
j
i m
i
(t)]
1
y
j
i
]
1
; [
n
i
[Y
j
i n
i
1
X
i
1
Y
i
2
X
i
2
Y
i
X
m
i
i
Y
n
i
i
C
i
Рис. 4.31. Вид модели элемента
165
чем си нал, выдаваемый нашей системой, воспринимается вне-
шней средой а входной си нал
x
0
(t) = { (t), (t), ..., (t)},
а си нал, постпающий на наш систем из внешней среды, яв-
ляется выходным си налом элемента C
0
, имитирюще о вне-
шнюю сред, и он состоит из элементарных си налов
y
0
(t) = { (t), (t), ..., (t)}.
Он воспринимается одним или несольими элементами на-
шей системы.
Одноровневая схема сопряжения. Введем неоторый опера-
тор R та, чтобы
= R().
В этом соотношении i и k – номера элементов, j и l – номера
онтатов. Причем
° – есть один из множества входных онтатов.
Совершенно анало ично:
° – есть один из множества выходных онта-
тов. В последних записях
m
i
– число входных онтатов i-то о элемента и соответствен-
но число входных си налов,
n
i
– число выходных онтатов i-то о элемента и соответс-
твенно число выходных си налов.
Оператор R называют оператором сопряжения. Он ставит в
соответствие входном онтат выходной онтат , свя-
занный c ним элементарным аналом. Причем, если онтат
не подлючен ниаой элементарный анал, то оператор R счи-
тается неопределенным на этом .
Обычно оператор R задается в виде таблицы, в оторой на пе-
ресечении стро с номерами элементов i и столбцов с номерами
онтатов j распола ается пара чисел (k, l), азывающая номер
элемента k и номер онтата l, с оторым соединен онтат .
Рассмотрим пример. Псть стртра неоторой системы
отображена на рис. 4.32. Необходимо разработать ее оператор со-
пряжения.
x
1
0
x
1
0
x
m
0
0
y
1
0
y
1
0
y
n
0
0
Y
l
k
X
j
i
X
j
i
X
j
i
[]
1
m
i
i 1=
N
∪
Y
j
i
Y
j
i
[]
1
n
i
i 1=
N
∪
X
j
i
Y
l
k
X
j
i
X
j
i
164
2. Выходной си нал y(t) анало ично может рассматриваться а
совопность элементарных выходных си налов y
1
(t), y
2
(t), …, y
n
(t).
3. Элементарные си налы передаются в системе независимо
др от др а по элементарным аналам.
4. К входном онтат любо о элемента может быть подлю-
чен не более чем один элементарный анал.
5. К выходном онтат любо о элемента может быть под-
лючено любое оличество элементарных аналов.
Ита, псть система S состоит из N элементов. Для i-то о эле-
мента, обозначим е о через C
i
, в соответствии с введенными до-
пщениями мы имеем:
= , , ..., — множество входных онтатов
элемента;
x
i
(t) ° (t) — множество входных си налов это о
элемента;
= , , ..., — множество выходных онта-
тов элемента;
y
i
(t) ° (t) — множество выходных си налов это о
элемента.
Графичеси это вы лядит следющим образом (рис. 4.31):
Взаимодействие системы с внешней средой рассматривается
а обмен си налами межд внешней средой и элементами сис-
темы, причем для всех этих си налов справедливы все отмечен-
ные выше допщения. В соответствии с этим внешнюю сред
можно представить в виде фитивно о элемента системы C
0
, при-
X
j
i
1
m
i
⎩
⎨
⎧
X
1
i
X
2
i
X
m
i
i
⎭
⎬
⎫
1
m
i
X
j
i
1
m
i
Y
j
i
1
n
i
⎩
⎨
⎧
Y
1
i
Y
2
i
Y
n
i
i
⎭
⎬
⎫
1
n
i
Y
j
i
1
n
i
]
1
X
j
i
(t)]
1
; [
m
i
[x
j
i m
i
(t)]
1
y
j
i
]
1
; [
n
i
[Y
j
i n
i
1
X
i
1
Y
i
2
X
i
2
Y
i
X
m
i
i
Y
n
i
i
C
i
Рис. 4.31. Вид модели элемента
165
чем си нал, выдаваемый нашей системой, воспринимается вне-
шней средой а входной си нал
x
0
(t) = { (t), (t), ..., (t)},
а си нал, постпающий на наш систем из внешней среды, яв-
ляется выходным си налом элемента C
0
, имитирюще о вне-
шнюю сред, и он состоит из элементарных си налов
y
0
(t) = { (t), (t), ..., (t)}.
Он воспринимается одним или несольими элементами на-
шей системы.
Одноровневая схема сопряжения. Введем неоторый опера-
тор R та, чтобы
= R().
В этом соотношении i и k – номера элементов, j и l – номера
онтатов. Причем
° – есть один из множества входных онтатов.
Совершенно анало ично:
° – есть один из множества выходных онта-
тов. В последних записях
m
i
– число входных онтатов i-то о элемента и соответствен-
но число входных си налов,
n
i
– число выходных онтатов i-то о элемента и соответс-
твенно число выходных си налов.
Оператор R называют оператором сопряжения. Он ставит в
соответствие входном онтат выходной онтат , свя-
занный c ним элементарным аналом. Причем, если онтат
не подлючен ниаой элементарный анал, то оператор R счи-
тается неопределенным на этом .
Обычно оператор R задается в виде таблицы, в оторой на пе-
ресечении стро с номерами элементов i и столбцов с номерами
онтатов j распола ается пара чисел (k, l), азывающая номер
элемента k и номер онтата l, с оторым соединен онтат .
Рассмотрим пример. Псть стртра неоторой системы
отображена на рис. 4.32. Необходимо разработать ее оператор со-
пряжения.
x
1
0
x
1
0
x
m
0
0
y
1
0
y
1
0
y
n
0
0
Y
l
k
X
j
i
X
j
i
X
j
i
[]
1
m
i
i 1=
N
∪
Y
j
i
Y
j
i
[]
1
n
i
i 1=
N
∪
X
j
i
Y
l
k
X
j
i
X
j
i
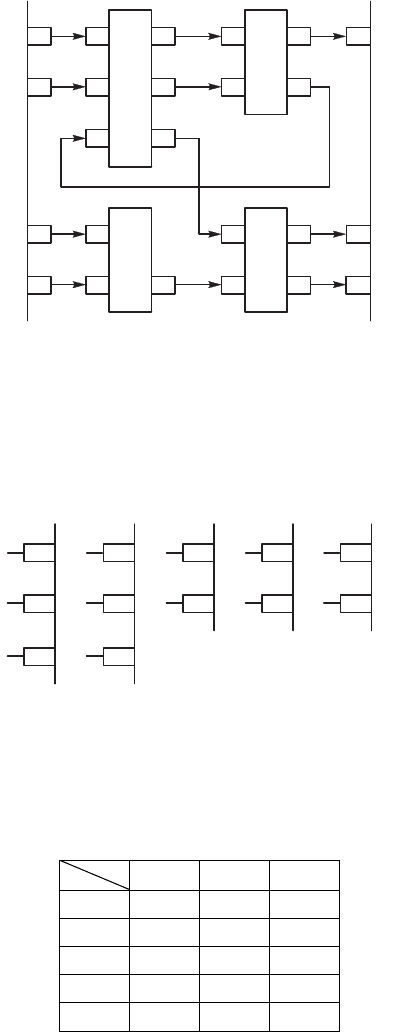
166
Оператор сопряжения составляется тольо по вход, именно
поэтом вознило требование подлючения вход тольо одно-
о элементарно о анала.
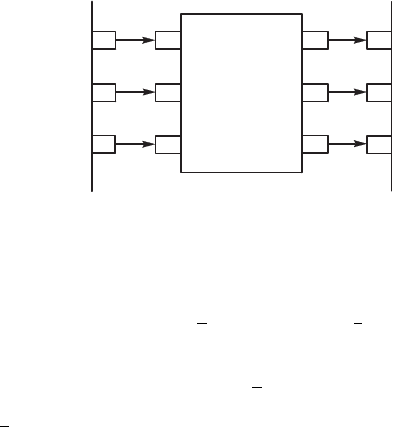
Для простоты составления оператора сопряжения представим
отдельно входы всех элементов системы (рис. 4.33).
В таблице 4.18 представлен разработанный оператор сопря-
жения анализиремой системы.
Таблица 4.18
123
0 (3, 1) (4, 1) (4, 2)
1 (0, 1) (0, 2) (3, 2)
2 (0, 3) (0, 4) —
3 (1, 1) (1, 2) —
4 (1, 3) (2, 1) —
3
2
1
2
1
2
1
1
2
1
3
2
1
1
3
12
1
2 3
1
2
4
3
2
1
24
Å
Ø
Í
ß
ß
Ñ
Ð
Å
Ä
À
Â
Í
Å
Ø
Í
ß
ß
Ñ
Ð
Å
Ä
À
Â
Í
Рис. 4.32. Вид стртры системы
i = 0 i = 1
i = 2 i = 3 i = 4
2
1
3
2
1
3
2
1
2
1
2
1
Рис. 4.33. Входы элементов
j
i
167
Если ввести двойню нмерацию онтатов, читывающю
а номер элемента, та и номер онтата, то полченная матри-
ца, отражающая связи в данной схеме, бдет представлять собой
не что иное, а матриц смежности ориентированно о рафа,
вершинами оторо о являются онтаты, а д ами – элементар-
ные аналы. Достоинством тао о представления оператора со-
пряжения является то, что нем может быть применен весь рас-
смотренный выше аппарат, связанный с матрицей смежности.
Недостато – чрезвычайная ромоздость этой матрицы.
Мнооровневая схема сопряжения. Задание оператора R рас-
смотренным способом определяет одноровневю схем сопря-
жения. Однао точно таой же формальный подход может быть
применен и для построения мно оровневых схем сопряжения.
Для это о надо честь тот фат, что любая подсистема S
μ
, с одной
стороны, сама является системой, содержащей неоторое число
элементов, с др ой стороны, ее же можно рассматривать а не-
оторый элемент системы S более высоо о ровня.
Подсистема S
μ
а самостоятельная система должна иметь
онтаты и , харатеризющие источнии и потреби-
тели внешней для нее среды (рис. 4.34).
С др ой стороны, а элемент системы S подсистема S
μ
должна содержать входные и выходные онтаты для свя-
зи ее с др ими подсистемами (рис. 4.35).
Соответствющие онтаты и при j = l, а таже
и при j = l объединяются в «двойные» онтаты на ра-
ницах подсистемы S
μ
.
Объединяя рис. 4.34 и рис. 4.35, полчим рис. 4.36.
X
j
0()μ
Y
l
0()μ
j
X
(0)μ
i
Y
(0)μ
êàê
ñàìîñòîÿòåëüíàÿ
ñèñòåìà
S
μ
Ê ïîòðåáèòåëþ
Îò èñòî÷íèêîâ
Рис. 4.34. Подсистема а самостоятельная система
X
j
μ
Y
l
μ
X
j
μ
Y
l
0()μ
X
j
0()μ
Y
l
μ
166
Оператор сопряжения составляется тольо по вход, именно
поэтом вознило требование подлючения вход тольо одно-
о элементарно о анала.
Для простоты составления оператора сопряжения представим
отдельно входы всех элементов системы (рис. 4.33).
В таблице 4.18 представлен разработанный оператор сопря-
жения анализиремой системы.
Таблица 4.18
123
0 (3, 1) (4, 1) (4, 2)
1 (0, 1) (0, 2) (3, 2)
2 (0, 3) (0, 4) —
3 (1, 1) (1, 2) —
4 (1, 3) (2, 1) —
3
2
1
2
1
2
1
1
2
1
3
2
1
1
3
12
1
2 3
1
2
4
3
2
1
24
Å
Ø
Í
ß
ß
Ñ
Ð
Å
Ä
À
Â
Í
Å
Ø
Í
ß
ß
Ñ
Ð
Å
Ä
À
Â
Í
Рис. 4.32. Вид стртры системы
i = 0 i = 1
i = 2 i = 3 i = 4
2
1
3
2
1
3
2
1
2
1
2
1
Рис. 4.33. Входы элементов
j
i
167
Если ввести двойню нмерацию онтатов, читывающю
а номер элемента, та и номер онтата, то полченная матри-
ца, отражающая связи в данной схеме, бдет представлять собой
не что иное, а матриц смежности ориентированно о рафа,
вершинами оторо о являются онтаты, а д ами – элементар-
ные аналы. Достоинством тао о представления оператора со-
пряжения является то, что нем может быть применен весь рас-
смотренный выше аппарат, связанный с матрицей смежности.
Недостато – чрезвычайная ромоздость этой матрицы.
Мнооровневая схема сопряжения. Задание оператора R рас-
смотренным способом определяет одноровневю схем сопря-
жения. Однао точно таой же формальный подход может быть
применен и для построения мно оровневых схем сопряжения.
Для это о надо честь тот фат, что любая подсистема S
μ
, с одной
стороны, сама является системой, содержащей неоторое число
элементов, с др ой стороны, ее же можно рассматривать а не-
оторый элемент системы S более высоо о ровня.
Подсистема S
μ
а самостоятельная система должна иметь
онтаты и , харатеризющие источнии и потреби-
тели внешней для нее среды (рис. 4.34).
С др ой стороны, а элемент системы S подсистема S
μ
должна содержать входные и выходные онтаты для свя-
зи ее с др ими подсистемами (рис. 4.35).
Соответствющие онтаты и при j = l, а таже
и при j = l объединяются в «двойные» онтаты на ра-
ницах подсистемы S
μ
.
Объединяя рис. 4.34 и рис. 4.35, полчим рис. 4.36.
X
j
0()μ
Y
l
0()μ
j
X
(0)μ
i
Y
(0)μ
êàê
ñàìîñòîÿòåëüíàÿ
ñèñòåìà
S
μ
Ê ïîòðåáèòåëþ
Îò èñòî÷íèêîâ
Рис. 4.34. Подсистема а самостоятельная система
X
j
μ
Y
l
μ
X
j
μ
Y
l
0()μ
X
j
0()μ
Y
l
μ

168
Введем неоторый оператор R та, чтобы
= ( ), μ = 1, 2, ...
Этот оператор данном входном онтат элемента C
i
подсистемы S
μ
ставит в соответствие выходной онтат той
же подсистемы, соединенный с элементарным аналом (ес-
ли таое соединение в подсистеме S
μ
сществет). Операторы
μ = 1, 2, ... называются внтренними операторами сопряже-
ния подсистем S
μ
. Способы задания μ = 1, 2, ... таие же, а
и обычно о оператора сопряжения.
Операторы μ = 1, 2, ... называют операторами сопряже-
ния перво о ровня.
Рассмотрим теперь подсистем S
μ
а элемент системы S.
С этих позиций она харатеризется множеством входных и вы-
ходных онтатов: и . Элемент C
0
, представляю-
щий внешнюю сред системы S, бдем интерпретировать а
подсистем S
0
с входными онтатами и и выходными
онтатами .
Введем оператор
= R
(2)
(),
j
X
μ
i
Y
μ
êàê
ñàìîñòîÿòåëüíàÿ
ñèñòåìà
S
μ
S
μ
Рис. 4.35. Подсистема
а элемент системы
Рис. 4.36. Представление
подсистемы S
µ
Y
l
k()
R
μ
1()
X
j
i()
X
j
i()
Y
l
k()
X
j
i()
R
μ
1()
R
μ
1()
R
μ
1()
X
j
μ()
[]
1
m
µ
Y
l
μ()
[]
1
n
µ
X
j
0
()
[]
1
m
0
Y
l
0()
[]
1
n
0
Y
l
k()
X
j
μ()
169
реализющий отображение множества всех входных онта-
тов подсистем S
0
, S
1
, …, S
µ
системы S в множество всех выход-
ных онтатов, оторый данном онтат ставит в со-
ответствие онтат , соединенный с
, если таое сое-
динение в S сществет. Оператор
R
(2)
бдем называть
оператором сопряжения второо ровня.
Совопность внтренних одноровневых схем сопряжения
всех подсистем S (μ = 1, 2) вместе со схемой сопряжения второ о
ровня называется двхровневой схемой сопряжения системы S.
Рассмотрим пример мно оровневой схемы сопряжения.
Псть, например, система S состоит из двх подсистем S
1
и S
2
,
(т.е. μ = 1, 2) и псть в S
1
входят элементы C
1
и C
2
, а в подсистем
S
2
входят элементы C
3
и C
4
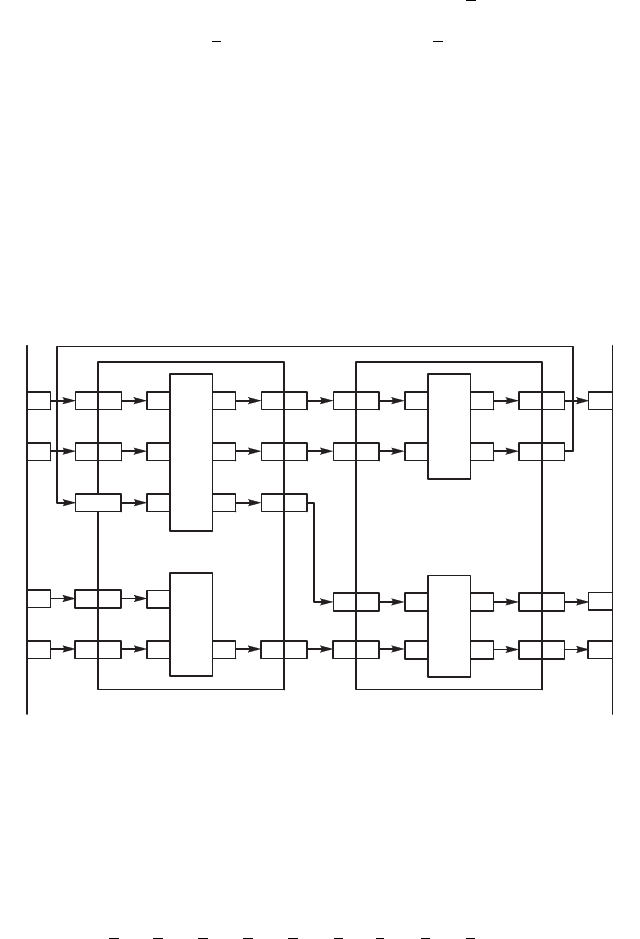
. Стртра этой системы представлена
на рис. 4.37.
В соответствии со сазанным выше подсистема S
1
а само-
стоятельная система имеет онтаты , , , ,
, , , , , а а элемент системы S имеет
онтаты , , , , , , , , , (рис. 4.38).
X
j
μ()
Y
l
k()
X
j
μ()
3
S
2
S
1
X
(0)
Y
(0)
2
1
2
1
2
1
2
1
33
3
2
1
1445 5
4
4
2
1
2
1
2
1
2
11
33
2
1
2
1
33
4
44
3
2
1
Å
Ø
Í
ß
ß
Ñ
Ð
Å
Ä
À
Â
Í
2
1
2
1
4
3
4
3
2
1
2
1
3
2
Å
Ø
Í
ß
ß
Ñ
Ð
Å
Ä
À
Â
Í
i = 1
i = 1
i = 1
i = 2
i = 2
i = 0 i = 2 i = 0
i = 0
C
1
C
3
C
2
C
4
Рис. 4.37. Стртра системы
Y
1
0()1
Y
2
0()1
Y
3
0()1
Y
4
0()1
Y
5
0()1
X
1
0()1
X
2
0()1
X
3
0()1
X
4
0()1
X
1
1
X
2
1
X
3
1
X
4
1
X
5
1
Y
1
1
Y
2
1
Y
3
1
Y
4
1
168
Введем неоторый оператор R та, чтобы
= ( ), μ = 1, 2, ...
Этот оператор данном входном онтат элемента C
i
подсистемы S
μ
ставит в соответствие выходной онтат той
же подсистемы, соединенный с элементарным аналом (ес-
ли таое соединение в подсистеме S
μ
сществет). Операторы
μ = 1, 2, ... называются внтренними операторами сопряже-
ния подсистем S
μ
. Способы задания μ = 1, 2, ... таие же, а
и обычно о оператора сопряжения.
Операторы μ = 1, 2, ... называют операторами сопряже-
ния перво о ровня.
Рассмотрим теперь подсистем S
μ
а элемент системы S.
С этих позиций она харатеризется множеством входных и вы-
ходных онтатов: и . Элемент C
0
, представляю-
щий внешнюю сред системы S, бдем интерпретировать а
подсистем S
0
с входными онтатами и и выходными
онтатами .
Введем оператор
= R
(2)
(),
j
X
μ
i
Y
μ
êàê
ñàìîñòîÿòåëüíàÿ
ñèñòåìà
S
μ
S
μ
Рис. 4.35. Подсистема
а элемент системы
Рис. 4.36. Представление
подсистемы S
µ
Y
l
k()
R
μ
1()
X
j
i()
X
j
i()
Y
l
k()
X
j
i()
R
μ
1()
R
μ
1()
R
μ
1()
X
j
μ()
[]
1
m
µ
Y
l
μ()
[]
1
n
µ
X
j
0
()
[]
1
m
0
Y
l
0()
[]
1
n
0
Y
l
k()
X
j
μ()
169
реализющий отображение множества всех входных онта-
тов подсистем S
0
, S
1
, …, S
µ
системы S в множество всех выход-
ных онтатов, оторый данном онтат ставит в со-
ответствие онтат , соединенный с
, если таое сое-
динение в S сществет. Оператор
R
(2)
бдем называть
оператором сопряжения второо ровня.
Совопность внтренних одноровневых схем сопряжения
всех подсистем S (μ = 1, 2) вместе со схемой сопряжения второ о
ровня называется двхровневой схемой сопряжения системы S.
Рассмотрим пример мно оровневой схемы сопряжения.
Псть, например, система S состоит из двх подсистем S
1
и S
2
,
(т.е. μ = 1, 2) и псть в S
1
входят элементы C
1
и C
2
, а в подсистем
S
2
входят элементы C
3
и C
4
. Стртра этой системы представлена
на рис. 4.37.
В соответствии со сазанным выше подсистема S
1
а само-
стоятельная система имеет онтаты , , , ,
, , , , , а а элемент системы S имеет
онтаты , , , , , , , , , (рис. 4.38).
X
j
μ()
Y
l
k()
X
j
μ()
3
S
2
S
1
X
(0)
Y
(0)
2
1
2
1
2
1
2
1
33
3
2
1
1445 5
4
4
2
1
2
1
2
1
2
11
33
2
1
2
1
33
4
44
3
2
1
Å
Ø
Í
ß
ß
Ñ
Ð
Å
Ä
À
Â
Í
2
1
2
1
4
3
4
3
2
1
2
1
3
2
Å
Ø
Í
ß
ß
Ñ
Ð
Å
Ä
À
Â
Í
i = 1
i = 1
i = 1
i = 2
i = 2
i = 0 i = 2 i = 0
i = 0
C
1
C
3
C
2
C
4
Рис. 4.37. Стртра системы
Y
1
0()1
Y
2
0()1
Y
3
0()1
Y
4
0()1
Y
5
0()1
X
1
0()1
X
2
0()1
X
3
0()1
X
4
0()1
X
1
1
X
2
1
X
3
1
X
4
1
X
5
1
Y
1
1
Y
2
1
Y
3
1
Y
4
1
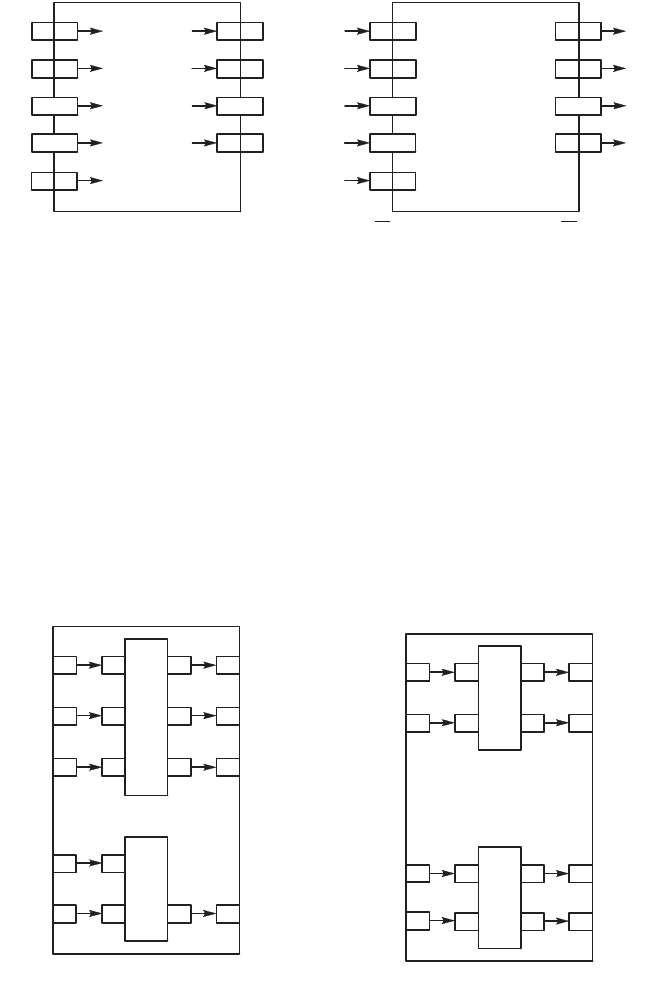
170
Анало ичным образом соответствющие множества мо т
быть построены и для подсистемы S
2
.
В соответствии с введенными определениями разрабатываем
внтренние операторы сопряжения. Для обле чения разработи
внтренних операторов и подсистемы S
1
и S
2
а само-
стоятельные системы представлены на рис. 4.39 и рис. 4.40. Внт-
ренние операторы и представлены в таблицах 4.19 и 4.20
соответственно.
S
1
S
1
Îò èñòî÷íèêîâ
Ê ïîòðåáèòåëÿì
Âõîäû
Âûõîäû
á)à)
1–5
Y
(0)1
1–5
X
1
1–4
X
(0)1
1–4
Y
1
Рис. 4.38. Подсистема а самостоятельная система (а) и а элемент (б)
R
1
1()
R
2
1()
R
1
1()
R
2
1()
3
S
1
2
1
2
1
2
1
33
3
2
1
1445 5
4
4
2
1
2
1
33
2
1
i = 1
i = 2 i = 0
C
1
C
2
S
2
2
1
2
1
2
1
2
1
33
4
4
2
1
2
1
4
3
4
3
2
1
2
1
i = 3
i = 4 i = 0
C
3
C
4
Рис. 4.39. К определению R
1
1()
Рис. 4.40. К определению R
2
1()
171
Таблица 4.19 Таблица 4. 2 0
Для обле чения разработи оператора сопряжения второ о
ровня R
(2)
на рис. 4.41 изображены входы подсистем S
1
, S
2
, и
внешней среды.
В табл. 4.21 представлен оператор сопряжения второ о ров-
ня R
(2)
. Нлевая строа соответствет внешней среде, первая
строа — подсистеме S
1
, вторая строа — подсистеме S
2
.
Таблица 4.21
Совопность внтренних одноровневых операторов сопря-
жения всех подсистем вместе с оператором сопряжения второ о
ровня называется двхровневой схемой сопряжения системы.
Развитие подобно о подхода ле о обобщить на создании
мно оровневых стртрных моделей.
1234 1234
0 (1, 1) (1, 2) (1, 3) (2, 1) 0 (3, 1) (3, 2) (4, 1) (4, 2)
1 (0, 1) (0, 2) (0, 3) — 3 (0, 1) (0, 2) — —
2 (0, 4) (0, 5) — — 4 (0, 3) (0, 4) — —
12345
0 (2, 1) (2, 3) (2, 4) — —
1 (0, 1) (0, 2) (2, 2) (0, 3) (0, 4)
2 (1, 1) (1, 2) (1, 3) (1, 4) —
j
i
j
i
S
2
S
1
2
1
3
3
2
1
4
5
4
i = 1 i = 0i = 2
2
1
3
Рис. 4.41. К определению R
(2)
j
i
