Меньков А.В., Острейковский В.А. Теоретические основы автоматизированного управления

Подождите немного. Документ загружается.

170

Анало ичным образом соответствющие множества мо т

быть построены и для подсистемы S

В соответствии с введенными определениями разрабатываем

внтренние операторы сопряжения. Для обле чения разработи

внтренних операторов и подсистемы S

и S

а само-

стоятельные системы представлены на рис. 4.39 и рис. 4.40. Внт-

ренние операторы и представлены в таблицах 4.19 и 4.20

соответственно.

Îò èñòî÷íèêîâ

Ê ïîòðåáèòåëÿì

Âõîäû

Âûõîäû

á)à)

1–5

(0)1

1–5

1–4

(0)1

1–4

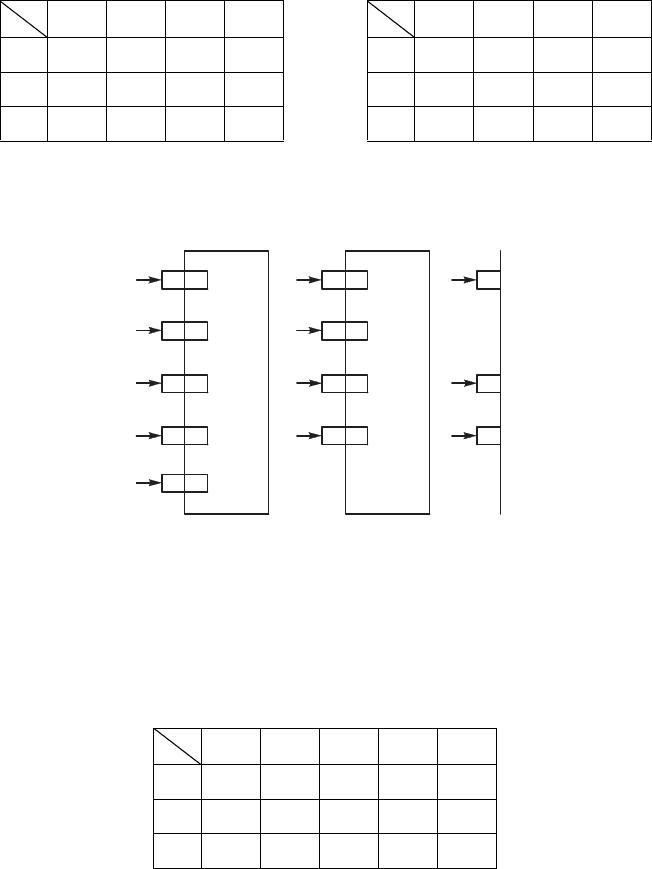
Рис. 4.38. Подсистема а самостоятельная система (а) и а элемент (б)

1()

1445 5

i = 1

i = 2 i = 0

i = 3

i = 4 i = 0

Рис. 4.39. К определению R

1()

Рис. 4.40. К определению R

1()

171

Таблица 4.19 Таблица 4. 2 0

Для обле чения разработи оператора сопряжения второ о

ровня R

(2)

на рис. 4.41 изображены входы подсистем S

, S

, и

внешней среды.

В табл. 4.21 представлен оператор сопряжения второ о ров-

ня R

(2)

. Нлевая строа соответствет внешней среде, первая

строа — подсистеме S

, вторая строа — подсистеме S

Таблица 4.21

Совопность внтренних одноровневых операторов сопря-

жения всех подсистем вместе с оператором сопряжения второ о

ровня называется двхровневой схемой сопряжения системы.

Развитие подобно о подхода ле о обобщить на создании

мно оровневых стртрных моделей.

1234 1234

0 (1, 1) (1, 2) (1, 3) (2, 1) 0 (3, 1) (3, 2) (4, 1) (4, 2)

1 (0, 1) (0, 2) (0, 3) — 3 (0, 1) (0, 2) — —

2 (0, 4) (0, 5) — — 4 (0, 3) (0, 4) — —

12345

0 (2, 1) (2, 3) (2, 4) — —

1 (0, 1) (0, 2) (2, 2) (0, 3) (0, 4)

2 (1, 1) (1, 2) (1, 3) (1, 4) —

i = 1 i = 0i = 2

Рис. 4.41. К определению R

(2)

172

Оператор преобразования. Ита, в соответствии с введенны-

ми выше определениями имеем:

° — один из множества элементарных вход-

ных си налов, воздействющих на i-тый элемент системы;

° – один из множества элементарных вы-

ходных си налов i-то о элемента системы.

Введем неоторый оператор F(t), таой, чтобы

= F(t){ (t)}.

Назовем е о оператором преобразования системы. Он ставит в

соответствие входном си нал (t) выходной си нал , свя-

занный с ним неоторым преобразованием.

Рассмотрим оператор преобразования i-то о элемента F

(t).

Е о можно задать азаниями следющих 3-х параметров:

— операции или оманды, т. е. азания, что надо делать, – f

;

— адреса, т. е. азания номера элемента и номера входно о

онтата, над оторым выполняется оманда i/;

— номера тата, на отором выполняется оманда, – t

То да оператор преобразования системы F(t) (табл. 4.22) мо-

жет быть задан с помощью матрицы,  оторой по строам пере-

числены все использемые оманды f

(проще в поряде их ис-

пользования), a по столбцам — таты, на оторых использется

данная оманда t

(проще в поряде возрастания номера тата);

на пересечении соответствющих стро и столбцов азывается

адрес элемента и входно о онтата i/ , над оторым выполня-

ется оманда.

Таблица 4.22

Перед разработой F(t) раф, отображающий принципиаль-

ню схем, должен быть порядочен по татам (с помощью одной

из методи, изложенных выше).

……..

i /

t() x

t()[]

i 0=

∪

t() y

t()[]

i 0=

∪

t() x

t()

173

Примеры оманд: сложить, вычесть, начислить %, ввести до-

мент в систем и т. п.

Алоритм разработи модели фнционирования оранизацион-

ной системы. Введем допщения:

1. Бдем считать, что любой домент, цирлирющий в сис-

теме, состоит из элементарных частей, содержащих тольо один

параметр – ревизит.

2. Назовем эт элементарню часть домента полем до-

мента.

3. Бдем считать, что связь межд доментами осществля-

ется через связь межд полями.

4. Бдем считать, что формирование любо о поля осщест-

вляется за два полтата:

— подача выходной информации  данном полю данно о

домента;

— преобразование входной информации в соответствии с не-

оторой фнцией.

При этом данное преобразование может осществляться а

с четом же содержащейся в этом поле информации, та и без

это о чета, но все да резльтирющая информация остается в

данном поле (рис. 4.42).

Таим образом, одно и то же поле до выполнения второ о по-

лтата является входным, после выполнения второ о полта-

та – выходным. В этом смысле можно считать, что поле имеет

несольо независимых в пространстве входов, посоль в одно

и то же поле может вноситься информация а из др их полей

данно о домента, та и из др их полей др их доментов, и

тольо один выход.

5. Бдем рассматривать поле Р а элемент системы D, D –

домент. В соответствии с материалом предыдще о пара рафа:

° — один из множества входов i-то о домента;

° – один из множества выходов i-то о домента.

Ôóíêöèîíàëüíîå

ïðåîáðàçîâàíèå

Îò äðóãèõ

ïîëåé

Ïîëå

äîêóìåíòà

Âõîä

Âûõîä

Рис. 4.42. К определению поля домента

i()

[]

i 0=

∪

i()

[]

i 0=

∪

172

Оператор преобразования. Ита, в соответствии с введенны-

ми выше определениями имеем:

° — один из множества элементарных вход-

ных си налов, воздействющих на i-тый элемент системы;

° – один из множества элементарных вы-

ходных си налов i-то о элемента системы.

Введем неоторый оператор F(t), таой, чтобы

= F(t){ (t)}.

Назовем е о оператором преобразования системы. Он ставит в

соответствие входном си нал (t) выходной си нал , свя-

занный с ним неоторым преобразованием.

Рассмотрим оператор преобразования i-то о элемента F

(t).

Е о можно задать азаниями следющих 3-х параметров:

— операции или оманды, т. е. азания, что надо делать, – f

;

— адреса, т. е. азания номера элемента и номера входно о

онтата, над оторым выполняется оманда i/;

— номера тата, на отором выполняется оманда, – t

То да оператор преобразования системы F(t) (табл. 4.22) мо-

жет быть задан с помощью матрицы,  оторой по строам пере-

числены все использемые оманды f

(проще в поряде их ис-

пользования), a по столбцам — таты, на оторых использется

данная оманда t

(проще в поряде возрастания номера тата);

на пересечении соответствющих стро и столбцов азывается

адрес элемента и входно о онтата i/ , над оторым выполня-

ется оманда.

Таблица 4.22

Перед разработой F(t) раф, отображающий принципиаль-

ню схем, должен быть порядочен по татам (с помощью одной

из методи, изложенных выше).

……..

i /

t() x

t()[]

i 0=

∪

t() y

t()[]

i 0=

∪

t() x

t()

173

Примеры оманд: сложить, вычесть, начислить %, ввести до-

мент в систем и т. п.

Алоритм разработи модели фнционирования оранизацион-

ной системы. Введем допщения:

1. Бдем считать, что любой домент, цирлирющий в сис-

теме, состоит из элементарных частей, содержащих тольо один

параметр – ревизит.

2. Назовем эт элементарню часть домента полем до-

мента.

3. Бдем считать, что связь межд доментами осществля-

ется через связь межд полями.

4. Бдем считать, что формирование любо о поля осщест-

вляется за два полтата:

— подача выходной информации  данном полю данно о

домента;

— преобразование входной информации в соответствии с не-

оторой фнцией.

При этом данное преобразование может осществляться а

с четом же содержащейся в этом поле информации, та и без

это о чета, но все да резльтирющая информация остается в

данном поле (рис. 4.42).

Таим образом, одно и то же поле до выполнения второ о по-

лтата является входным, после выполнения второ о полта-

та – выходным. В этом смысле можно считать, что поле имеет

несольо независимых в пространстве входов, посоль в одно

и то же поле может вноситься информация а из др их полей

данно о домента, та и из др их полей др их доментов, и

тольо один выход.

5. Бдем рассматривать поле Р а элемент системы D, D –

домент. В соответствии с материалом предыдще о пара рафа:

° — один из множества входов i-то о домента;

° – один из множества выходов i-то о домента.

Ôóíêöèîíàëüíîå

ïðåîáðàçîâàíèå

Îò äðóãèõ

ïîëåé

Ïîëå

äîêóìåíòà

Âõîä

Âûõîä

Рис. 4.42. К определению поля домента

i()

[]

i 0=

∪

i()

[]

i 0=

∪

174

В залючение приведем обобщенный ал оритм разработи

формальной модели фнционирования.

Исходные данные:

а) схема доментооборота;

б) фнциональные обязанности операторов системы.

Эти данные полчаются либо в резльтате обследования же

фнционирющей ор анизационной стртры, либо при ее

проетировании.

В соответствии с фнциями ор анизационной системы раз-

рабатывается ал оритм обработи информации.

1. Производится нмерация элементов системы.

2. Для аждо о элемента системы нмерются все е о входы и

выходы.

3. Производится порядочение элементов системы.

4. Разрабатывается оператор сопряжения R.

5. Разрабатывается оператор преобразования F(t).

6. Разрабатывается моделирющий ал оритм.

Подобное описание может быть использовано для любо о

ровня:

— первый ровень – ровень полей доментов, то да поле

является элементом системы, домент – системой;

— второй ровень – ровень доментов, то да домент яв-

ляется элементом, омплет доментов – системой;

— третий ровень – ровень омплетов доментов, то да

омплет доментов бдет элементом, ор анизация в це-

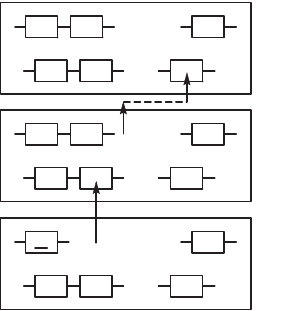
лом (например, бан) – системой (рис. 4.43).

Óðîâåíü 3Óðîâåíü 2Óðîâåíü 1

Рис. 4.43. Уровни описания

175

4.8. Пример разработи модели фнционирования

оранизационной системы

Словесное описание процесса фнционирования. Псть 

неоторо о пользователя домашней лоальной сети, именемо о

впоследствии лиентом, вознила необходимость продлить свой

абонемент пользования Интернетом на аой-то сро. С этой це-

лью он прибывает в офис администраторов сети, де производят

эт операцию.

Введём следющие допщения, не снижающие общности

постанови задачи:

— лиент распола ает требемой сммой,

— очередь лиентов отстствет.

На время обслживания лиента формирется система, со-

стоящая из лиента, администратора и ЭВМ-администратора.

Рассмотрим фнции всех элементов системы:

Фнции лиента:

— Передача администратор достоверения пользователя се-

ти (УПС), в отором, в числе проче о, содержится ло ин

это о пользователя.

— Словесное азание, на аой месяц нжно оформить або-

немент.

— Оплата стоимости абонемента.

— Полчение УПС и чеа.

Фнции администратора:

— Идентифиация лиента по данным УПС.

— Ввод в ЭВМ оплаченно о сроа действия абонемента и

сммы, оторю заплатил лиент.

— Передача лиент УПС и чеа об оплате.

Фнции ЭВМ:

— Ативирование пользования Интернетом для данно о ли-

ента на оплачиваемый сро.

— Выдача чеа, в отором азываются фамилия админист-

ратора, принявше о платеж, ло ин лиента, оплаченный

сро действия абонемента, смма, оторю заплатил ли-

ент, дата.

Оранизационная схема системы. Ор анизационная схема со-

ставляется на основе словесно о описания, приведенно о в пре-

дыдщем разделе.

Ита, на время обслживания лиента формирется система:

лиент, администратор, ЭВМ, стртрная схема оторой пред-

ставлена на рис. 4.44.

174

В залючение приведем обобщенный ал оритм разработи

формальной модели фнционирования.

Исходные данные:

а) схема доментооборота;

б) фнциональные обязанности операторов системы.

Эти данные полчаются либо в резльтате обследования же

фнционирющей ор анизационной стртры, либо при ее

проетировании.

В соответствии с фнциями ор анизационной системы раз-

рабатывается ал оритм обработи информации.

1. Производится нмерация элементов системы.

2. Для аждо о элемента системы нмерются все е о входы и

выходы.

3. Производится порядочение элементов системы.

4. Разрабатывается оператор сопряжения R.

5. Разрабатывается оператор преобразования F(t).

6. Разрабатывается моделирющий ал оритм.

Подобное описание может быть использовано для любо о

ровня:

— первый ровень – ровень полей доментов, то да поле

является элементом системы, домент – системой;

— второй ровень – ровень доментов, то да домент яв-

ляется элементом, омплет доментов – системой;

— третий ровень – ровень омплетов доментов, то да

омплет доментов бдет элементом, ор анизация в це-

лом (например, бан) – системой (рис. 4.43).

Óðîâåíü 3Óðîâåíü 2Óðîâåíü 1

Рис. 4.43. Уровни описания

175

4.8. Пример разработи модели фнционирования

оранизационной системы

Словесное описание процесса фнционирования. Псть 

неоторо о пользователя домашней лоальной сети, именемо о

впоследствии лиентом, вознила необходимость продлить свой

абонемент пользования Интернетом на аой-то сро. С этой це-

лью он прибывает в офис администраторов сети, де производят

эт операцию.

Введём следющие допщения, не снижающие общности

постанови задачи:

— лиент распола ает требемой сммой,

— очередь лиентов отстствет.

На время обслживания лиента формирется система, со-

стоящая из лиента, администратора и ЭВМ-администратора.

Рассмотрим фнции всех элементов системы:

Фнции лиента:

— Передача администратор достоверения пользователя се-

ти (УПС), в отором, в числе проче о, содержится ло ин

это о пользователя.

— Словесное азание, на аой месяц нжно оформить або-

немент.

— Оплата стоимости абонемента.

— Полчение УПС и чеа.

Фнции администратора:

— Идентифиация лиента по данным УПС.

— Ввод в ЭВМ оплаченно о сроа действия абонемента и

сммы, оторю заплатил лиент.

— Передача лиент УПС и чеа об оплате.

Фнции ЭВМ:

— Ативирование пользования Интернетом для данно о ли-

ента на оплачиваемый сро.

— Выдача чеа, в отором азываются фамилия админист-

ратора, принявше о платеж, ло ин лиента, оплаченный

сро действия абонемента, смма, оторю заплатил ли-

ент, дата.

Оранизационная схема системы. Ор анизационная схема со-

ставляется на основе словесно о описания, приведенно о в пре-

дыдщем разделе.

Ита, на время обслживания лиента формирется система:

лиент, администратор, ЭВМ, стртрная схема оторой пред-

ставлена на рис. 4.44.

176

Описание доментов системы. Описание доментооборота

составляется на основе материала двх предыдщих пара рафов.

Ка следет из них, доментооборот влючает в себя два до-

мента: УПС и че.

Рассмотрим прощенню схем доментооборота (рис.4.45),

на оторой отразим тольо те взаимосвязи межд домента-

ми, оторые использются для реализации рассматриваемой

операции.

Êëèåíò

ÓÏÑ, ÷åê

Ïîòðåáíîñòü

â àáîíåìåíòå

Àäìèíè-

ñòðàòîð

Ïàìÿòü

ÝÂÌ

×åê

Âíåøíÿÿ ñðåäà

Ëîãèí,

ñóììà,

îïåðàöèÿ,

îïëà÷èâàåìûé

ñðîê

ÓÏÑ,

äåíüãè,

îïåðàöèÿ

Äàòà,

ôàìèëèÿ

àäìèíèñòðàòîðà

Âíåøíÿÿ ñðåäà

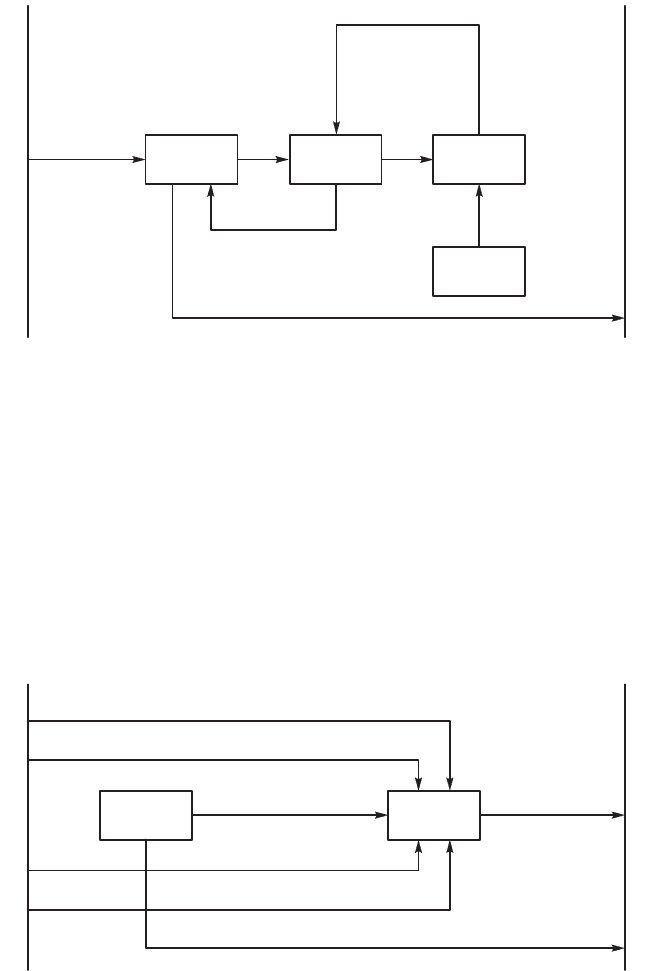
Рис. 4.44. Оранизационная схема системы

Ëîãèí

Ñóììà

Îïëà÷èâàåìûé ñðîê

ÓÏÑ

(D1)

×ÅÊ

(D2)

Ôàìèëèÿ àäìèíèñòðàòîðà

Âíåøíÿÿ ñðåäà

Êëèåíòó

Äàòà

Рис. 4.45. Урпненная схема доментооборота

177

На рис. 4.46 и 4.47 представлены стилизованные, но очень

близие  подлинни формы азанных доментов. Содер-

жание этих доментов расрывается в словесном описании.

Поля данных доментов пронмерованы в произвольном по-

ряде

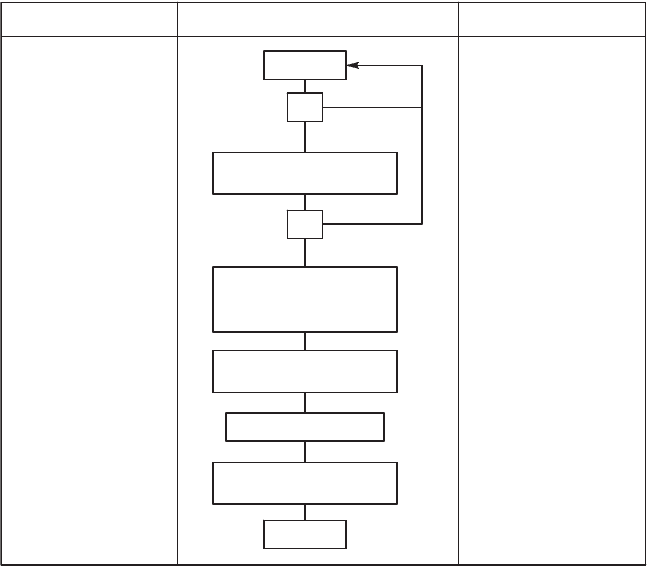
Урпненный алоритм обработи информации. На рис. 4.48

представлен ал оритм обработи информации, составленный на

основе словесно о описания процесса фнционирования сис-

темы.

На рис. 4.48 обозначены:

– i-тый тат движения доментов;

– обозначение i-той процедры, содержание оторой рас-

рыто в названии i-то о блоа ал оритма;

– i-тая оманда словно о перехода.

В отличие от F

она не изменяет содержимо о доментов.

Тат движения доментов не читывает оманды словно о пе-

рехода, а тат работы ал оритма читывает их.

Конретные словия:

– есть ли  лиента потребность оформить абонемент на

пользование Интернетом на следющий месяц;

– провера сществования в сети пользователя, соответс-

твюще о данном УПС.

Разработа принципиальной схемы доментооборота. Для это-

о необходимо перенмеровать все доменты и все поля этих до-

ментов. Это сделано в разделе «Описание доментов». При-

îãèí ïîëüçîâàòåëÿ

ÔÈÎ ïîëüçîâàòåëÿ

¹ ÓÏÑ

îãèí ïîëüçîâàòåëÿ

Ñóììà

Îïëà÷åííûé ñðîê

Ôàìèëèÿ àäìèíèñòðàòîðà

àòà

Рис. 4.46. Домент D1. Форма УПС

Рис. 4.47. Домент D2. Форма чеа

176

Описание доментов системы. Описание доментооборота

составляется на основе материала двх предыдщих пара рафов.

Ка следет из них, доментооборот влючает в себя два до-

мента: УПС и че.

Рассмотрим прощенню схем доментооборота (рис.4.45),

на оторой отразим тольо те взаимосвязи межд домента-

ми, оторые использются для реализации рассматриваемой

операции.

Êëèåíò

ÓÏÑ, ÷åê

Ïîòðåáíîñòü

â àáîíåìåíòå

Àäìèíè-

ñòðàòîð

Ïàìÿòü

ÝÂÌ

×åê

Âíåøíÿÿ ñðåäà

Ëîãèí,

ñóììà,

îïåðàöèÿ,

îïëà÷èâàåìûé

ñðîê

ÓÏÑ,

äåíüãè,

îïåðàöèÿ

Äàòà,

ôàìèëèÿ

àäìèíèñòðàòîðà

Âíåøíÿÿ ñðåäà

Рис. 4.44. Оранизационная схема системы

Ëîãèí

Ñóììà

Îïëà÷èâàåìûé ñðîê

ÓÏÑ

(D1)

×ÅÊ

(D2)

Ôàìèëèÿ àäìèíèñòðàòîðà

Âíåøíÿÿ ñðåäà

Êëèåíòó

Äàòà

Рис. 4.45. Урпненная схема доментооборота

177

На рис. 4.46 и 4.47 представлены стилизованные, но очень

близие  подлинни формы азанных доментов. Содер-

жание этих доментов расрывается в словесном описании.

Поля данных доментов пронмерованы в произвольном по-

ряде

Урпненный алоритм обработи информации. На рис. 4.48

представлен ал оритм обработи информации, составленный на

основе словесно о описания процесса фнционирования сис-

темы.

На рис. 4.48 обозначены:

– i-тый тат движения доментов;

– обозначение i-той процедры, содержание оторой рас-

рыто в названии i-то о блоа ал оритма;

– i-тая оманда словно о перехода.

В отличие от F

она не изменяет содержимо о доментов.

Тат движения доментов не читывает оманды словно о пе-

рехода, а тат работы ал оритма читывает их.

Конретные словия:

– есть ли  лиента потребность оформить абонемент на

пользование Интернетом на следющий месяц;

– провера сществования в сети пользователя, соответс-

твюще о данном УПС.

Разработа принципиальной схемы доментооборота. Для это-

о необходимо перенмеровать все доменты и все поля этих до-

ментов. Это сделано в разделе «Описание доментов». При-

îãèí ïîëüçîâàòåëÿ

ÔÈÎ ïîëüçîâàòåëÿ

¹ ÓÏÑ

îãèí ïîëüçîâàòåëÿ

Ñóììà

Îïëà÷åííûé ñðîê

Ôàìèëèÿ àäìèíèñòðàòîðà

àòà

Рис. 4.46. Домент D1. Форма УПС

Рис. 4.47. Домент D2. Форма чеа

178

нципиальная схема разрабатывается на основе все о предыдще-

о материала. На схеме знаом «

» обозначены операции над всем

доментом в целом. Для добства чтения схемы внешняя среда,

обозначим ее через 0, бдет состоять из 3-х составляющих: 01 –

лиент; 02 – администратор; 03 – ЭВМ.

Изобразим все доменты, частвющие в доментообороте.

Сначала изображаем со всеми входными и выходными онтата-

ми внешнюю сред и все доменты, частвющие в обработе

информации. Слева – выходы внешней среды, справа – входы

внешней среды. На аждом доменте слева – входы, а справа –

выходы. Нмерем по поряд все выходные онтаты внешней

среды от 1 до 6. Затем нмерем по поряд, начиная с 7, все вы-

ходы доментов. Заводим все входные и выходные онтаты,

а внешней среды, та и всех доментов в общю шин. Затем

реализем блои ал оритма [t

, F

; t

, F

; t

, F

; t

, F

; t

, F

]

(рис. 4.49)

, F

Òàêò, ïðîöåäóðà Àëãîðèòì Èñïîëíèòåëü

Íà÷àëî

íåò

Êëèåíò

Àäìèíèñòðàòîð

Àäìèíèñòðàòîð,

ÝÂÌ

Êëèåíò,

àäìèíèñòðàòîð,

äà

Ïåðåäà÷à îïåðàòîðó

ÓÏÑ

Ââîä ÷åðåç ÝÂÌ

îïëà÷åííîãî ñðîêà,

ëîãèíà, ñóììû

Ïåðåíîñ ïîëÿ ëîãèí

â ÷åê

Çàïîëíåíèå ÷åêà

Ïåðåäà÷à êëèåíòó

D1 è D2

Êîíåö

íåò

Рис. 4.48. Алоритм обработи информации

179

Оператор сопряжения. На основе принципиальной схемы и

ал оритма обработи информации разрабатываем оператор со-

пряжения R (табл.4.23).

Таблица 4.23

*123456789

01 D1/* D2/*

02 D1/1 D1/2 D1/3

03 D1/2 02/4 02/3 03/5

D1 01/1

D2 03/6 02/2 D1/2 02/3 02/4 02/5

Ëîãèí

¹ ÓÏÑ

D2(÷åê)

D1(ÓÏÑ)

Ëîãèí

Ñóììà

Îïëà÷åííûé

Ôàìèëèÿ

Äàòà

ÔÈÎ

* *

3 7

Ïîëó÷åíèå

ÓÏÑ

Ïðîâåðêà

ñóùåñòâîâàíè

ïîëüçîâàòåëÿ

ñ òàêèì ÓÏÑ

0303

Ââîä:

ëîãèí

ñóììà,

ñðîê,

ñðîê

äàòà

Ââîä:

ÓÏÑ

ôàìèëèÿ

àäìèíèñòðàòîðà,

àäìèíèñòðàòîðà

îïëà÷åííûé

ñðîê, ñóììà,

äàòà

Ðàñïå÷àòêà

÷åêà

Рис. 4.49. Принципиальная схема доментооборота

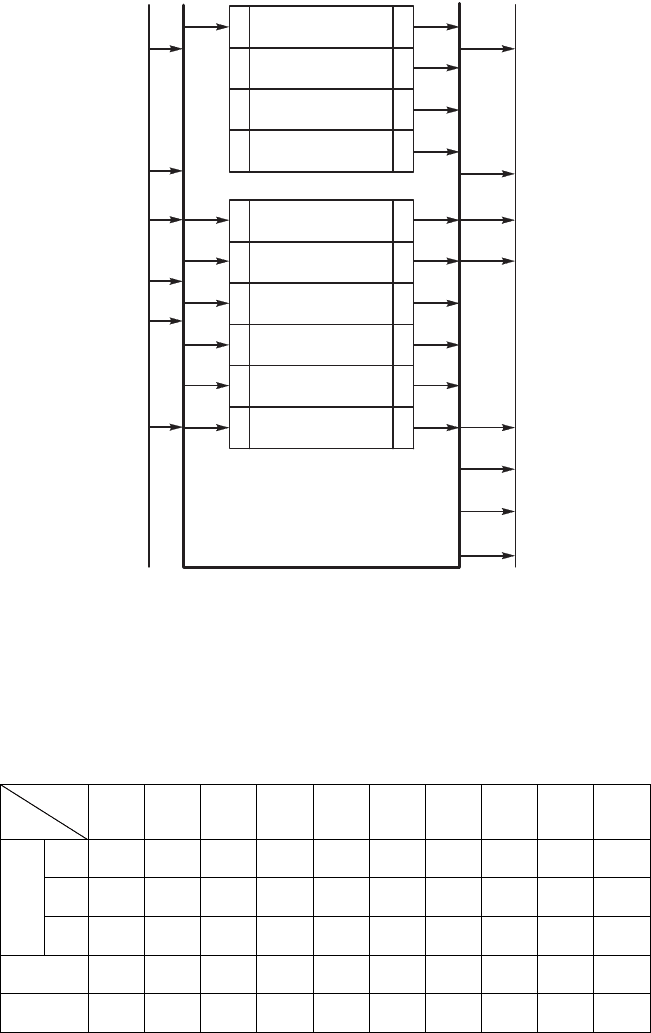
178

нципиальная схема разрабатывается на основе все о предыдще-

о материала. На схеме знаом «

» обозначены операции над всем

доментом в целом. Для добства чтения схемы внешняя среда,

обозначим ее через 0, бдет состоять из 3-х составляющих: 01 –

лиент; 02 – администратор; 03 – ЭВМ.

Изобразим все доменты, частвющие в доментообороте.

Сначала изображаем со всеми входными и выходными онтата-

ми внешнюю сред и все доменты, частвющие в обработе

информации. Слева – выходы внешней среды, справа – входы

внешней среды. На аждом доменте слева – входы, а справа –

выходы. Нмерем по поряд все выходные онтаты внешней

среды от 1 до 6. Затем нмерем по поряд, начиная с 7, все вы-

ходы доментов. Заводим все входные и выходные онтаты,

а внешней среды, та и всех доментов в общю шин. Затем

реализем блои ал оритма [t

, F

; t

, F

; t

, F

; t

, F

; t

, F

]

(рис. 4.49)

, F

Òàêò, ïðîöåäóðà Àëãîðèòì Èñïîëíèòåëü

Íà÷àëî

íåò

Êëèåíò

Àäìèíèñòðàòîð

Àäìèíèñòðàòîð,

ÝÂÌ

Êëèåíò,

àäìèíèñòðàòîð,

äà

Ïåðåäà÷à îïåðàòîðó

ÓÏÑ

Ââîä ÷åðåç ÝÂÌ

îïëà÷åííîãî ñðîêà,

ëîãèíà, ñóììû

Ïåðåíîñ ïîëÿ ëîãèí

â ÷åê

Çàïîëíåíèå ÷åêà

Ïåðåäà÷à êëèåíòó

D1 è D2

Êîíåö

íåò

Рис. 4.48. Алоритм обработи информации

179

Оператор сопряжения. На основе принципиальной схемы и

ал оритма обработи информации разрабатываем оператор со-

пряжения R (табл.4.23).

Таблица 4.23

*123456789

01 D1/* D2/*

02 D1/1 D1/2 D1/3

03 D1/2 02/4 02/3 03/5

D1 01/1

D2 03/6 02/2 D1/2 02/3 02/4 02/5

Ëîãèí

¹ ÓÏÑ

D2(÷åê)

D1(ÓÏÑ)

Ëîãèí

Ñóììà

Îïëà÷åííûé

Ôàìèëèÿ

Äàòà

ÔÈÎ

* *

3 7

Ïîëó÷åíèå

ÓÏÑ

Ïðîâåðêà

ñóùåñòâîâàíè

ïîëüçîâàòåëÿ

ñ òàêèì ÓÏÑ

0303

Ââîä:

ëîãèí

ñóììà,

ñðîê,

ñðîê

äàòà

Ââîä:

ÓÏÑ

ôàìèëèÿ

àäìèíèñòðàòîðà,

àäìèíèñòðàòîðà

îïëà÷åííûé

ñðîê, ñóììà,

äàòà

Ðàñïå÷àòêà

÷åêà

Рис. 4.49. Принципиальная схема доментооборота

180

Оператор преобразования F (t). На основе ал оритма обработ-

и информации и принципиальной схемы доментооборота

расрываем все операторы F(t). На аждом тате t

(j = 1–5) вы-

полняется один оператор F

(t).

, F

– передача оператор УПС. Вводим элементарню о-

манд f

– передача домента. F

= f

(D1/*).

, F

– ввод в память ЭВМ ло ина, сроа и сммы. Вводим

элементарню оманд f

– ввод домента в целом или полей

домента. F

= f

(D1/2, 02/3, 02/4).

, F

– перенос поля ло ин домента D1 в соответствющее

поле домента D2. Вводим элементарню оманд f

– перенос.

= f

(D1/2 → D2/2). t

, F

– ввод в че полей: фамилия адми-

нистратора, оплаченный сро, смма, дата. F

= f

(D2/1, D2/3,

D2/4, D2/5).

, F

– передача лиент D1/* и D2/*. F

= f

(D1/*, D2/*).

Резльтаты сводим в табл. 4.24 – оператор преобразования

системы.

Таблица 4.24

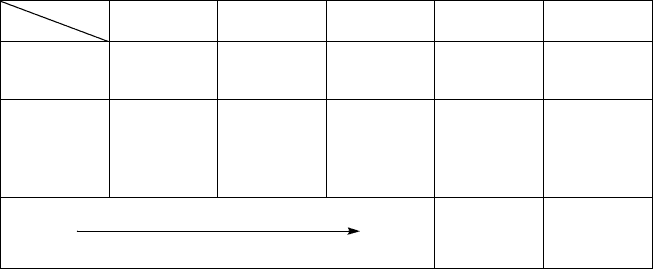
Примечание. В операции «Перенос», очевидно, необходимо азы-

вать два адреса: отда брать и да направлять. В табл. 4.24 это поазано

с помощью стрели.

Моделирющий алоритм. Разработаем неоторый автомат A,

состояниями оторо о были бы таты доментооборота t

, де

j = 1, 2, 3, 4, 5, а выходным алфавитом это о автомата – элемен-

тарные оманды f

, i = 1, 2, 3. Ка отмечалось выше, на аждом

тате t

выполняется одна или несольо оманд f

, имеющих не-

нлевой списо ар ментов. Эта информация определяется на

основе оператора преобразования F(t) (табл. 4.24). На тате t

ни-

аие элементарные оманды не выполняются. Данный автомат

моделирет переходы системы из одно о состояния в др ое толь-

D1/* D1/*

D2/*

D1/2

02/3

02/4

D2/1

D2/3

D2/4

D2/5

D2/2D1/2

лоин

181

о в зависимости от словий ϕ

. Причем если «да», то ϕ

, если

«нет», то . Поведение автомата описывается табл. 4.25, оторая

составляется на основе ал оритма обработи информации. В от-

личие от оманд f

, j

таже переводит систем из одно о состоя-

ния в др ое, но она не изменяет содержимо о ни одно о из до-

ментов.

Таблица 4.25

Таим образом, модель фнционирования ор анизационной

системы представлена автоматом, оператором преобразования

F(t), оператором сопряжения R и моделирющим ал оритмом

(автоматом).

Для ее реализации необходимо заодировать элементарные

оманды f

в виде подпро рамм, а сам автомат — в виде лавно о

модля. При работе автомата необходимо пользоваться операто-

ром F(t), чтобы определять элементарню оманд, выполняемю

в тещем тате, и оператором R, чтобы станавливать источнии

информации, подаваемой на входы доментов, обрабатываемых

с помощью f

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Перечислите цели и задачи стртрно(о анализа АСУ.

2. Рассмотрите пти совершенствования ор(анизационной, фнцио-

нальной, ал(оритмичесой стртр.

3. Назовите ровни описания стртры АСУ.

4. Сформлирйте формализованные способы описания стртры АСУ.

Номер

перехода

Тещее состояние Условие Следющее состояние

1 t

2—

3 t

4—

5 t

— t

6 t

— t

7 t

— t

8 t

— t