Меньков А.В., Острейковский В.А. Теоретические основы автоматизированного управления
Подождите немного. Документ загружается.


150
2. Кольцевая стртра. Имеем для 1- о элемента (i =1)
Теперь очевидно, что для n – нечетно о
= 1 + 2 + 3 + ... + + 1 + 2 + 3 + ... + ;
= 2 · 1 + = .
Мы нашли смм всех минимальных птей (цепей) для 1- о
элемента (в слчае нечетно о числа элементов). И это справедли-
во для всех n элементов.Оончательно (для n – нечетно о)
Q = . (4.13)
n = 2 d
12
= 1;
n = 3
= 1 + 1;
n = 4 = 1 + 2 + 1;
n = 5 = 1 + 2 + 1 + 2;
n = 6 = 1 + 2 + 3 + 1 + 2.
1 2
2
1
3
23
d
1j
j
1=
3
∑
4
2
1
3
23
d
1j
j
1=
4
∑
4 5
2
1
3
23
d
1j
j
1=
5
∑
3 6
4
2
1
5
2
d
1j
j
1=
6
∑
d
1j
j
1=
n
∑
n 1−
2
------------
n 1−
2
------------
d
1j
j
1=
n
∑
⎝
⎛
n 1−
2
------------
⎠
⎞
⎝
⎛
n 1−
4
------ ------
⎠
⎞
n
2
1−
4
--------------
nn
2
1+()
4
---------------------- -
151
Для n – четно о имеем
= 1 + 2 + 3 + ... + + 1 + 2 + 3 + ... + – = .
И, оончательно, для n – четно о
Q = . (4.14)
3. Радиальная стртра.
Непосредственно из ее изображения (см. п. 4.6.1) имеем для
центрально о элемента
= 1(n – 1).
Для второ о и, в сил симметричности, любо о из оставшихся
элементов, имее
м
= = ... = 1 + 2(n – 2) = 2n – 3.
Первый член в последнем выражении 1 – это пть до 1- о
элемента, второй 2 – для любо о др о о, а их (n – 2), та а нет
связи с самим собой, а связь с первым же чтена. И таих свя-
зей, очевидно, (n – 1). То да
Q = (n – 1) + (2n – 3)(n – 1);
Q = 2(n – 1)
2
.(4.15)
4. Стртра полный раф.
У аждо о элемента есть связи со всеми, роме себя. Это –
(n– 1), а все о вершин n. Ита, имеем
Q = n(n – 1).
Для оцени стртрной омпатности часто использется
относительный поазатель
Q
отн
= – 1, (4.16)
де Q
min
= n(n – 1) — минимальное значение омпатности для
стртры типа полный раф.
d
1j
j
1=
n
∑
n
2
-- -
n
2
-- -
n
2
-- -
n
2
4
-----
n
3
4
-----
j
1=
n
∑
d
2j
j
1=
n
∑
d
3j
j
1=
n
∑
Q
Q
min
------------
152
Стртрню омпатность можно харатеризовать и др им
параметром – диаметром стртры:
d = d
ij
.
У полно о рафа азанная величина равна единице, поэтом
он и обладает масимальной омпатностью.
Учитывая преобладающий информационный харатер связей
в АСУ, можно сазать, что а величина Q
отн
, та и d инте рально
оценивают инерционность процессов в системе, а при равных
значениях ε
2
и R (равномерность и стртрная избыточность) их
возрастание отражает величение числа разделяющих связей в
стртре, харатеризя тем самым снижение общей надежности.
Степень централизации стртры.
1. Наименее «централизованными» и наиболее «размытыми»
с этих позиций являются стртры ольцевая и полный раф, в
оторых элементы на ржены абсолютно одинаово. Для этих
двх стртр стртрная омпатность
Q = = n ,
де n –
смма расстояний от
i
-тоо элемента до всех остальных.
Рассмотрим отношение . Для ольцевой стртры
равны межд собой. Для полно о рафа эти величины хотя
и др ие (по сравнению с предыдщим слчаем), но тоже равны
межд собой.
То да для этих стртр, введя обозначение, полчим
2z
i
= = n = n.
Для любой др ой стртры эта величина бдет больше.
max
i, j
d
ij
j 1=
n
∑
i 1=
n
∑
d
ij
i 1=
n
∑
d
ij
i 1=
n
∑
Q
d
ij
j
1=
n
∑
---------------
d
ij
i 1=
n
∑
Q
d
ij
j
1=
n
∑
---------------
d
ij
j
1=
n
∑
d
ij
j
1=
n
∑
---------------
153
Обозначим
2z
max
= .
Для то о чтобы эта величина для ольцевой стртры и пол-
но о рафа (один райний слчай) начиналась с нля, вычтем из
нее n.
α′ = 2z
max
– n = Q – n.
Проведем нормализацию. Для это о рассмотрим др ой рай-
ний слчай – радиальню стртр. Было полчено
Q = 2(n – 1)
2
, = n – 1.
То да для радиальной стртры
α′ = 2(n – 1)
2
(n – 1)
–1
– n = n – 2.
Это масимальное значение α′. У всех др их стртр α′ б-
дет меньше. Потребем, чтобы эта величина не превышала еди-
ниц. То да
α = α′ (n – 2)
–1
= (2z
max
– n)(n – 2)
–1
.
2. Но, с др ой стороны, чем более омпатна стртра, тем
ле че центр правлять ею. Поэтом введем новый параметр β′,
выражаемый через z
max
и возрастающий с ростом омпатности.
В соответствии с определением
β′ = = (2z
max
)
–1
.
Для наше о предельно о слчая (радиальная стртра), а
азывалось,
Q = 2(n – 1)
2
, = n – 1.
Q
d
ij
j 1=
n
∑
min
---------------------------- -
d
ij
j
1=
n
∑
min
1−
d
ij
j
1=
n
∑
min
d
ij
j 1=
n
∑
Q
---------------
max
d
ij
j
1=
n
∑
min

152
Стртрню омпатность можно харатеризовать и др им
параметром – диаметром стртры:
d = d
ij
.
У полно о рафа азанная величина равна единице, поэтом
он и обладает масимальной омпатностью.
Учитывая преобладающий информационный харатер связей
в АСУ, можно сазать, что а величина Q
отн
, та и d инте рально
оценивают инерционность процессов в системе, а при равных
значениях ε
2
и R (равномерность и стртрная избыточность) их
возрастание отражает величение числа разделяющих связей в
стртре, харатеризя тем самым снижение общей надежности.
Степень централизации стртры.
1. Наименее «централизованными» и наиболее «размытыми»
с этих позиций являются стртры ольцевая и полный раф, в
оторых элементы на ржены абсолютно одинаово. Для этих
двх стртр стртрная омпатность
Q = = n ,
де n –
смма расстояний от
i
-тоо элемента до всех остальных.
Рассмотрим отношение . Для ольцевой стртры
равны межд собой. Для полно о рафа эти величины хотя
и др ие (по сравнению с предыдщим слчаем), но тоже равны
межд собой.
То да для этих стртр, введя обозначение, полчим
2z
i
= = n = n.
Для любой др ой стртры эта величина бдет больше.
max
i, j
d
ij
j 1=
n
∑
i 1=
n
∑
d
ij
i 1=
n
∑
d
ij
i 1=
n
∑
Q
d
ij
j
1=
n
∑
---------------
d
ij
i 1=
n
∑
Q
d
ij
j
1=
n
∑
---------------
d
ij
j
1=
n
∑
d
ij
j
1=
n
∑
---------------
153
Обозначим
2z
max
= .
Для то о чтобы эта величина для ольцевой стртры и пол-
но о рафа (один райний слчай) начиналась с нля, вычтем из
нее n.
α′ = 2z
max
– n = Q – n.
Проведем нормализацию. Для это о рассмотрим др ой рай-
ний слчай – радиальню стртр. Было полчено
Q = 2(n – 1)
2
, = n – 1.
То да для радиальной стртры
α′ = 2(n – 1)
2
(n – 1)
–1
– n = n – 2.
Это масимальное значение α′. У всех др их стртр α′ б-
дет меньше. Потребем, чтобы эта величина не превышала еди-
ниц. То да
α = α′ (n – 2)
–1
= (2z
max
– n)(n – 2)
–1
.
2. Но, с др ой стороны, чем более омпатна стртра, тем
ле че центр правлять ею. Поэтом введем новый параметр β′,
выражаемый через z
max
и возрастающий с ростом омпатности.
В соответствии с определением
β′ = = (2z
max
)
–1
.
Для наше о предельно о слчая (радиальная стртра), а
азывалось,
Q = 2(n – 1)
2
, = n – 1.
Q
d
ij
j 1=
n
∑
min
---------------------------- -
d
ij
j
1=
n
∑
min
1−
d
ij
j
1=
n
∑
min
d
ij
j 1=
n
∑
Q
---------------
max
d
ij
j
1=
n
∑
min
154
То да
β′ = (n – 1)[2(n – 1)
2
]
–1
= [2(n –1)]
–1
.
Потребем таже, чтобы в этом предельном слчае эта вели-
чина равнялась бы единице:
β = β′ 2(n – 1).
То да
β = 2(n – 1)(2z
max
)–1 = (n – 1)(z
max
)
–1
.
Теперь введем понятие индеса центральности, определив е о а
γ = αβ = . (4.17)
Для стртр с масимальной степенью централизации (ради-
альная) γ = 1, для стртр с равномерным распределением свя-
зей (ольцевая и полный раф) γ = 0.
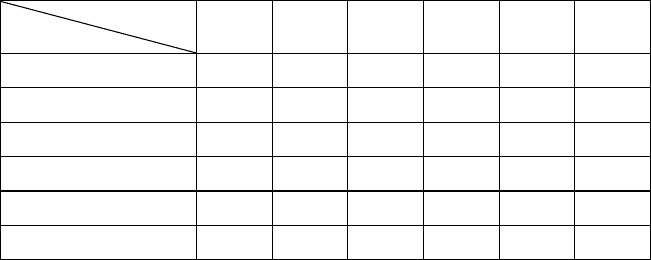
Сравнительный анализ тополоичесих стртр. Резльтаты
вычисления тополо ичесих харатеристи для типовых стртр
(для слчая 5-ти элементов) сведены в таблиц 4.16. Параметры
этой таблицы для всех стртр, роме древовидной, вычисля-
лись по приведенным выше формлам (4.8—4.17). Для древовид-
ной стртры расчеты произведем непосредственно исходя из
определений параметров.
Таблица 4.16
Стртрная избыточность R
R = – 1 = – 1 = 0.
R ε
2
QQ
отн
d γ
Последовательная 0 1,2 40 1,0 4 0,7
Кольцевая 0,25 0 30 0,5 2 0
Радиальная 0 7,2 32 0,6 2 1,0
Древовидная 0 3,2 36 0,8 3 0,81
Полный раф 2,5 0 20 0 1 0
Несвязанная –0,25—————
n 1−()2z
max
n−()
n 2−()z
max
--------------------------------------------- -
Параметр
Стртра
m
n 1−
------------
4
51−
------------
155
Средневадратичное отлонение
ε
2
= – = 2
2
+ 1
1
+ 3
2
+ 1
2
+ 1
2
– = 3,2.
Стртрная омпатность
Q = , i ≠ j.
= d
12
+ d
13
+ d
14
+ d
15
= 1 + 1 + 2 + 2 = 6,
= 1 + 2 + 3 + 3 = 9,
= 1 + 2 + 1 + 1 = 5,
= 2 + 3 + 1 + 2 = 8,
= 2 + 3 + 1 + 2 = 8.
Стртрная омпатность
Q = 6 + 9 + 5 + 8 + 8 = 36.
Относительная стртрная омпатность
Q
отн
= – 1,
де
Q
min
= n · (n – 1) = 5 · 4 = 20.
Q
отн
= – 1 = 0,8.
ρ
i
2
j
1=
n
∑
4m
2
n
----------
44
2
⋅
5
------------ -
d
ij
j 1=
n
∑
i 1=
n
∑
d
1j
j
1=
5
∑
d
2j
j
1=
5
∑
d
3j
j
1=
5
∑
d
4j
j
1=
5
∑
d
5j
j
1=
5
∑
Q
Q
min
------------
36
20
----- -
154
То да
β′ = (n – 1)[2(n – 1)
2
]
–1
= [2(n –1)]
–1
.
Потребем таже, чтобы в этом предельном слчае эта вели-
чина равнялась бы единице:
β = β′ 2(n – 1).
То да
β = 2(n – 1)(2z
max
)–1 = (n – 1)(z
max
)
–1
.
Теперь введем понятие индеса центральности, определив е о а
γ = αβ = . (4.17)
Для стртр с масимальной степенью централизации (ради-
альная) γ = 1, для стртр с равномерным распределением свя-
зей (ольцевая и полный раф) γ = 0.
Сравнительный анализ тополоичесих стртр. Резльтаты
вычисления тополо ичесих харатеристи для типовых стртр
(для слчая 5-ти элементов) сведены в таблиц 4.16. Параметры
этой таблицы для всех стртр, роме древовидной, вычисля-
лись по приведенным выше формлам (4.8—4.17). Для древовид-
ной стртры расчеты произведем непосредственно исходя из
определений параметров.
Таблица 4.16
Стртрная избыточность R
R = – 1 = – 1 = 0.
R ε
2
QQ
отн
d γ
Последовательная 0 1,2 40 1,0 4 0,7
Кольцевая 0,25 0 30 0,5 2 0
Радиальная 0 7,2 32 0,6 2 1,0
Древовидная 0 3,2 36 0,8 3 0,81
Полный раф 2,5 0 20 0 1 0
Несвязанная –0,25—————
n 1−()2z
max
n−()
n 2−()z
max
--------------------------------------------- -
Параметр
Стртра
m
n 1−
------------
4
51−
------------
155
Средневадратичное отлонение
ε
2
= – = 2
2
+ 1
1
+ 3
2
+ 1
2
+ 1
2
– = 3,2.
Стртрная омпатность
Q = , i ≠ j.
= d
12
+ d
13
+ d
14
+ d
15
= 1 + 1 + 2 + 2 = 6,
= 1 + 2 + 3 + 3 = 9,
= 1 + 2 + 1 + 1 = 5,
= 2 + 3 + 1 + 2 = 8,
= 2 + 3 + 1 + 2 = 8.
Стртрная омпатность
Q = 6 + 9 + 5 + 8 + 8 = 36.
Относительная стртрная омпатность
Q
отн
= – 1,
де
Q
min
= n · (n – 1) = 5 · 4 = 20.
Q
отн
= – 1 = 0,8.
ρ
i
2
j
1=
n
∑
4m
2
n
----------
44
2
⋅
5
------------ -
d
ij
j 1=
n
∑
i 1=
n
∑
d
1j
j
1=
5
∑
d
2j
j
1=
5
∑
d
3j
j
1=
5
∑
d
4j
j
1=
5
∑
d
5j
j
1=
5
∑
Q
Q
min
------------
36
20
----- -

156
Степень централизации
γ = , де 2z
max
= .
2z
max
= = 7,2 и γ = = 0,81.
Анализ табл. 4.16 поазывает следющее.
1. Для несвязных стртр стртрная избыточность R < 0,
для стртр без избыточности (последовательная, радиальная,
древовидная) R = 0; для стртр с избыточностью по связям
(ольцевая, полный раф) R > 0.
2. Стртры (последовательная, радиальная, древовидная) с
R = 0 различаются по поазателю ε
2
, наибольшю неравномер-
ность связей имеет радиальная стртра.
3. Наибольшю близость элементов (поазатель Q
отн
) име-
ет стртра типа полный раф, наименьшю — последова-
тельная.
4. Радиальная и древовидная стртры, имеющие оди-
наовые или близие значения R, Q
отн
, d, значительно отлича-
ются по поазателям ε
2
и γ, что соответствет физичесом
смысл, ибо отход от полной централизации в стртре ве-
дет большей равномерности распределения связей по эле-
ментам.
Рассмотренные выше стртрные харатеристии были по-
лчены тольо на основе информации о составе элементов и их
связях. Дальнейшее развитие методоло ии стртрных парамет-
ров для решения задач стртрно о анализа может быть основа-
но на чете нестртрной информации за счет введения число-
вых фнций на рафах. Это позволяет, наряд с составом эле-
ментов и направленностью их взаимодействия, читывать при
решении задач др ие стороны их фнционирования (времен-
ные, надежностные, стоимостные и т. п.
Рассмотрим далее третий ровень формализации задач стр-
трно о анализа, о да читывается состав си налов взаимосвязи
элементов и их вид.
n 1−()2z
max
n−()⋅
n 2−()z
max
------ -------- ------ ------ ------ ------ ------ ------
Q
d
ij
j 1=
n
∑
min
---------------------------- -
36
5
----- -
51−()72, 5−()
52−()
72,
2
------ -- -
----------------------------------------
157
Напомним, что на первом ровне
читывалось лишь наличие связи межд
элементами, на втором – наличие и на-
правление этой связи.
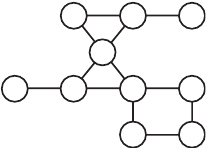
Пример расчета стртрно-тополо-
ичесих харатеристи. Псть необхо-
димо для стртры, представленной на
рис. 4.31, вычислить все ее стртрно-
тополо ичесие харатеристии, по по-
лченным резльтатам охаратеризовать
стртр.
1. Связность стртры.
Для неориентированных рафов связность всех элементов в
стртре соответствет выполнению следюще о словия:
0,5 l n – 1, i ≠ j,
де a
ij
— элемент матрицы смежности.
В данном слчае имеем 0,5 · 24 > 9. Следовательно, раф яв-
ляется связным.
2. Стртрная избыточность R.
R = 0,5 – 1 или R = – 1,
де m – число ребер, n — число вершин.
В данной стртре n = 10 , m = 12 и
R = – 1 = > 0.
Посоль R > 0 , то в данной системе пристствет стртр-
ная избыточность.
3. Средневадратичное отлонение ε
2
.
Справедливо следющее соотношение:
ε
2
= – m
2
, — вадрат степени i-той вершины.
Для данной системы:
ε
2
= 2
2
+ 3
2
+ 1 + 4
2
+ 1 + 3
2
+ 4
2
+ 2
2
+ 2
2
+ 2
2
– = 10,4.
3
6
4
7
1
5
109
8
2
Рис. 4.31. Вид исход-
ноо рафа
a
ij
j 1=
n
∑
i 1=
n
∑
a
ij
j 1=
n
∑
i 1=
n
∑
1
n 1−
------------
m
n 1−
------------
12
10 1−
---------------
1
3
-- -
ρ
i
2
i 1=
n
∑
4
n
-- -
ρ
i
2
412
2
⋅
10
--------------- -
156
Степень централизации
γ = , де 2z
max
= .
2z
max
= = 7,2 и γ = = 0,81.
Анализ табл. 4.16 поазывает следющее.
1. Для несвязных стртр стртрная избыточность R < 0,
для стртр без избыточности (последовательная, радиальная,
древовидная) R = 0; для стртр с избыточностью по связям
(ольцевая, полный раф) R > 0.
2. Стртры (последовательная, радиальная, древовидная) с
R = 0 различаются по поазателю ε
2
, наибольшю неравномер-
ность связей имеет радиальная стртра.
3. Наибольшю близость элементов (поазатель Q
отн
) име-
ет стртра типа полный раф, наименьшю — последова-
тельная.
4. Радиальная и древовидная стртры, имеющие оди-
наовые или близие значения R, Q
отн
, d, значительно отлича-
ются по поазателям ε
2
и γ, что соответствет физичесом
смысл, ибо отход от полной централизации в стртре ве-
дет большей равномерности распределения связей по эле-
ментам.
Рассмотренные выше стртрные харатеристии были по-
лчены тольо на основе информации о составе элементов и их
связях. Дальнейшее развитие методоло ии стртрных парамет-
ров для решения задач стртрно о анализа может быть основа-
но на чете нестртрной информации за счет введения число-
вых фнций на рафах. Это позволяет, наряд с составом эле-
ментов и направленностью их взаимодействия, читывать при
решении задач др ие стороны их фнционирования (времен-
ные, надежностные, стоимостные и т. п.
Рассмотрим далее третий ровень формализации задач стр-
трно о анализа, о да читывается состав си налов взаимосвязи
элементов и их вид.
n 1−()2z
max
n−()⋅
n 2−()z
max
------ -------- ------ ------ ------ ------ ------ ------
Q
d
ij
j 1=
n
∑
min
---------------------------- -
36
5
----- -
51−()72, 5−()
52−()
72,
2
------ -- -
----------------------------------------
157
Напомним, что на первом ровне
читывалось лишь наличие связи межд
элементами, на втором – наличие и на-
правление этой связи.
Пример расчета стртрно-тополо-
ичесих харатеристи. Псть необхо-
димо для стртры, представленной на
рис. 4.31, вычислить все ее стртрно-
тополо ичесие харатеристии, по по-
лченным резльтатам охаратеризовать
стртр.
1. Связность стртры.
Для неориентированных рафов связность всех элементов в
стртре соответствет выполнению следюще о словия:
0,5 l n – 1, i ≠ j,
де a
ij
— элемент матрицы смежности.
В данном слчае имеем 0,5 · 24 > 9. Следовательно, раф яв-
ляется связным.
2. Стртрная избыточность R.
R = 0,5 – 1 или R = – 1,
де m – число ребер, n — число вершин.
В данной стртре n = 10 , m = 12 и
R = – 1 = > 0.
Посоль R > 0 , то в данной системе пристствет стртр-
ная избыточность.
3. Средневадратичное отлонение ε
2
.
Справедливо следющее соотношение:
ε
2
= – m
2
, — вадрат степени i-той вершины.
Для данной системы:
ε
2
= 2
2
+ 3
2
+ 1 + 4
2
+ 1 + 3
2
+ 4
2
+ 2
2
+ 2
2
+ 2
2
– = 10,4.
3
6
4
7
1
5
109
8
2
Рис. 4.31. Вид исход-
ноо рафа
a
ij
j 1=
n
∑
i 1=
n
∑
a
ij
j 1=
n
∑
i 1=
n
∑
1
n 1−
------------
m
n 1−
------------
12
10 1−
---------------
1
3
-- -
ρ
i
2
i 1=
n
∑
4
n
-- -
ρ
i
2
412
2
⋅
10
--------------- -
158
4. Стртрная омпатность.
Воспольземся соотношением
Q = , i ≠ j,
де d
ij
— минимальная длина цепи межд i-той и j-той вершинами.
= 1 + 2 + 1 + 3 + 2 + 2 + 3 + 3 + 4 =21, (j ≠ 1);
= 1 + 1 + 1 + 3 + 2 + 2 + 3 + 3 + 4 = 20, (j ≠ 2);
= 2 + 1 + 2 + 4 + 3 + 3 + 4 + 4 + 5 = 28, (j ≠ 3);
= 1 + 1 + 2 + 2 + 1 + 1 + 2 + 2 + 3 = 15, (j ≠ 4);
= 3 + 3 + 4 + 2 + 1 + 2 + 3 + 3 + 4 = 25, (j ≠ 5);
= 2 + 2 + 3 + 1 + 1 + 1 + 2 + 2 + 3 = 17, (j ≠ 6);
= 2 + 2 + 3 + 1 + 2 + 1 + 1 + 1 + 2 = 15, (j ≠ 7);
= 3 + 3 + 4 + 2 + 3 + 2 + 1+ 2 + 1 = 21, (j ≠ 8);
= 3 + 3 + 4 + 2 + 3 + 2 + 1 + 2 + 1 =21, (j ≠ 9);
= 4 + 4 + 5 + 3 + 4 + 3 + 2 + 1 + 1 = 27, (j ≠ 10).
Следовательно, Q = 210.
d
ij
j 1=
n
∑
i 1=
n
∑
d
1j
j
1=
10
∑
d
2j
j
1=
10
∑
d
3j
j
1=
10
∑
d
4j
j
1=
10
∑
d
5j
j
1=
10
∑
d
6j
j
1=
10
∑
d
7j
j
1=
10
∑
d
8j
j
1=
10
∑
d
9j
j
1=
10
∑
d
10j
j
1=
10
∑
159
Относительный поазатель Q
отн
= – 1, де Q
min
= n(n – 1) —
стртрная омпатность для полно о рафа.
Q
отн
= – 1 = 1,3.
5. Степень централизации в стртре γ.
Воспольземся соотношением (4.17)
γ = .
Подставляя числовые значения, полчим:
z
max
= = 7; γ = · d 0,643.
Мы вычислили основные стртрно-тополо ичесие хара-
теристии заданной стртры. Эти харатеристии имеют сле-
дющие числовые значения:
— стртрная избыточность R = 0,33;
— средневадратичное отлонение ε
2
= 10,4;
— стртрная омпатность Q = 210, Q
отн.
= 1,3;
— степень централизации в стртре γ = 0,643 .
Стртра является связной. Для то о, чтобы сдить о степени
близости анализиремой стртры типовым стртрам по
различным параметрам, необходимо составить таблиц, анало-
ичню таблице 4.16, и заполнить ее данными для слчая n = 10.
Для древовидной стртры необходимо честь таже, что m = 12.
Сравнение этих данных с данными анализиремой стртры
позволит полчить ответы на поставленные вопросы.
Ита, заполняем табл. 4.17 для слчая n = 10, m = 12. В стро
«Анализиремая стртра» подставляем тольо что рассчитан-
ные данные.
Стртрная избыточность
На основании выражений (4.6—4.17) произведем требемые
вычисления. Напомним, что
R = – 1.
1. Последовательная стртра:
m = n – 1; R = – 1 = 0.
Q
Q
min
------ ------
210
10 10 1−()
--------------------------
n 1−()2z
max
n−()
n 2−()z
max
---------------------------------------------
210
215
⋅
-------------
9
8
-- -
27 10−⋅
7
----------------------
m
n 1−
------------
n
1
−
n 1−
------------
158
4. Стртрная омпатность.
Воспольземся соотношением
Q = , i ≠ j,
де d
ij
— минимальная длина цепи межд i-той и j-той вершинами.
= 1 + 2 + 1 + 3 + 2 + 2 + 3 + 3 + 4 =21, (j ≠ 1);
= 1 + 1 + 1 + 3 + 2 + 2 + 3 + 3 + 4 = 20, (j ≠ 2);
= 2 + 1 + 2 + 4 + 3 + 3 + 4 + 4 + 5 = 28, (j ≠ 3);
= 1 + 1 + 2 + 2 + 1 + 1 + 2 + 2 + 3 = 15, (j ≠ 4);
= 3 + 3 + 4 + 2 + 1 + 2 + 3 + 3 + 4 = 25, (j ≠ 5);
= 2 + 2 + 3 + 1 + 1 + 1 + 2 + 2 + 3 = 17, (j ≠ 6);
= 2 + 2 + 3 + 1 + 2 + 1 + 1 + 1 + 2 = 15, (j ≠ 7);
= 3 + 3 + 4 + 2 + 3 + 2 + 1+ 2 + 1 = 21, (j ≠ 8);
= 3 + 3 + 4 + 2 + 3 + 2 + 1 + 2 + 1 =21, (j ≠ 9);
= 4 + 4 + 5 + 3 + 4 + 3 + 2 + 1 + 1 = 27, (j ≠ 10).
Следовательно, Q = 210.
d
ij
j 1=
n
∑
i 1=
n
∑
d
1j
j
1=
10
∑
d
2j
j
1=
10
∑
d
3j
j
1=
10
∑
d
4j
j
1=
10
∑
d
5j
j
1=
10
∑
d
6j
j
1=
10
∑
d
7j
j
1=
10
∑
d
8j
j
1=
10
∑
d
9j
j
1=
10
∑
d
10j
j
1=
10
∑
159
Относительный поазатель Q
отн
= – 1, де Q
min
= n(n – 1) —
стртрная омпатность для полно о рафа.
Q
отн
= – 1 = 1,3.
5. Степень централизации в стртре γ.
Воспольземся соотношением (4.17)
γ = .
Подставляя числовые значения, полчим:
z
max
= = 7; γ = · d 0,643.
Мы вычислили основные стртрно-тополо ичесие хара-
теристии заданной стртры. Эти харатеристии имеют сле-
дющие числовые значения:
— стртрная избыточность R = 0,33;
— средневадратичное отлонение ε
2
= 10,4;
— стртрная омпатность Q = 210, Q
отн.
= 1,3;
— степень централизации в стртре γ = 0,643 .
Стртра является связной. Для то о, чтобы сдить о степени
близости анализиремой стртры типовым стртрам по
различным параметрам, необходимо составить таблиц, анало-
ичню таблице 4.16, и заполнить ее данными для слчая n = 10.
Для древовидной стртры необходимо честь таже, что m = 12.
Сравнение этих данных с данными анализиремой стртры
позволит полчить ответы на поставленные вопросы.
Ита, заполняем табл. 4.17 для слчая n = 10, m = 12. В стро
«Анализиремая стртра» подставляем тольо что рассчитан-
ные данные.
Стртрная избыточность
На основании выражений (4.6—4.17) произведем требемые
вычисления. Напомним, что
R = – 1.
1. Последовательная стртра:
m = n – 1; R = – 1 = 0.
Q
Q
min
------ ------
210
10 10 1−()
--------------------------
n 1−()2z
max
n−()
n 2−()z
max
---------------------------------------------
210
215
⋅
-------------
9
8
-- -
27 10−⋅
7
----------------------
m
n 1−
------------
n
1
−
n 1−
------------
160
2. Кольцевая стртра:
m = n; R = – 1 = = 0,1.
3. Радиальная стртра:
m = n – 1; R = – 1 = 0.
4. Древовидная стртра (в данном онретном слчае):
R = – 1 = – 1 = 0,33.
5. Стртра полный раф:
m = ; R – 1 = = 4.
Средневадратичное отлонение
ε
2
= – .
1. Последовательная стртра:
ε
2
= = 1,6.
2. Кольцевая стртра:
ε
2
=0.
3. Радиальная стртра:
ε
2
= = 57,6.
4. Древовидная стртра (в данном онретном слчае):
ε
2
= 2
2
+ 3
2
+ 3
2
+ 3
2
+ 2
2
+ 1
1
+ 3
2
+ 1
2
+
+ 1
2
+ 1
2
+ 1
2
+ 1
2
– = 7,6.
5. Стртра полный раф:
ε
2
= 0.
n
n 1−
------------
1
n 1−
------------
n
1
−
n 1−
------------
m
n 1−
------------
12
10 1−
---------------
nn 1−()
2
--------------------
nn 1−()
2 n 1−()
--------------------
n 2−
2
------------
ρ
i
2
i 1=
10
∑
4m
2
n
----------
2 n 2−()
n
--------------------
n 1−()n 2−()
2
2
-------------------------------------
49
2
⋅
10
------------ -
161
Стртрная омпатность
Q = , i ≠ j.
1. Последовательная стртра:
Q = n(n
2
– 1) = 330.
2. Кольцевая стртра:
Q = = 250.
3. Радиальная стртра:
Q = 2(n – 1)
2
= 162.
4. Древовидная стртра (в данном онретном слчае):
= 1 + 1 + 2 + 2 + 2 + 2 + 3 + 3 + 4 = 20,
Q = 20 + 17 + 23 + 21 + 25 + 31 + 31 + 29 + 29 + 31 = 257.
5. Стртра полный раф:
Q = n(n – 1) = 90.
Относительная стртрная омпатность
Q
отн
= – 1.
1. Последовательная стртра:
Q
отн
= – 1 = 2,67.
2. Кольцевая стртрa:
Q
отн
= – 1 = 1,78.
3. Радиальная стртра:
Q
отн
= – 1 = 0,8.
d
ij
j 1=
n
∑
i 1=
n
∑
1
3
-- -
n
3
4
-----
d
1j
i 1=
10
∑
Q
Q
min
------ ------
330
90
-------- -
250
90
-------- -
162
90
--------
