Меньков А.В., Острейковский В.А. Теоретические основы автоматизированного управления

Подождите немного. Документ загружается.

120

Контром называется таой онечный

пть,  оторо о начальная вершина первой д-

и совпадает с онечной вершиной последней

д и. Например, для рафа (рис. 4.3) последо-

вательность д (1, 3), (3, 5), (5, 1) есть онтр

(рис. 4.7).

Длиной цепи (пти) называют число ребер (д ),

входящих в цепь (пть) рафа.

Матрица смежности вершин рафа А является матрицей не-

посредственных птей рафа, имеющих длин, равню единице.

Общее число транзитных птей длиной λ может быть полчено в

резльтате возведения в λ-тю степень матрицы А:

= A

λ–1

Элемент матрицы A

(λ) определяет число птей длиной λ

от вершины i  вершине j.

На рис. 4.8 приведен пример определения элементов матрицы.

Степень вершины. Число ребер, инцидентных вершине i не-

ориентированно о рафа, называют степенью вершины i и обозна-

чают ρ(i).

Для рафа, представленно о на рис. 4.4:

ρ(1) = 4; ρ(2) = 1; ρ(3) = 3; ρ(4) = 2; ρ(5) = 2. ρ(i) = 12.

Или в общем виде 0,5 = m, де n — число вершин, m —

число ребер рафа.

1 3

Рис. 4.7.

Вид онтра

i j

λ = 1, a

= 1

λ = 2, a

= 1

λ = 2, a

= 2

λ = 3, a

= 2

Рис. 4.8. Пример элементов матрицы А

i 1=

∑

i 1=

∑

121

Число д ориентированно о рафа, оторые имеют началь-

ной вершиной вершин i, называют полстепенью исхода верши-

ны i и обозначают через ρ

(i). Анало ично, число д , оторые

имеют своей онечной вершиной вершин j, называют полсте-

пенью захода вершины j и обозначают через ρ

–

(j). Для рафа,

представленно о на рис. 4.3:

(1) = 2; ρ

(2) = 0; ρ

(3) = 2; ρ

(4) = 1; ρ

(5) = 2; ρ

(i) = 7.

–

(1) = 1; ρ

–

(2) = 3; ρ

–

(3) = 1; ρ

–

(4) = 1; ρ

–

(5) = 1; ρ

–

(j) = 7.

Или в общем виде ρ

(i) = ρ

–

(j), де m — число д ра-

фа, n — число вершин рафа.

К понятию связности рафа. Для неориентированных ра-

фов вводится понятие слабой связности или просто связности.

Граф G (V) называется слабо связным (связным), если для

любых вершин рафа i и j сществет цепь из вершины i в вер-

шин j.

Для ориентированных рафов вводится дополнительное по-

нятие сильной связности. Граф G(V) называется сильно связным,

если для любых вершин рафа i, j сществет пть из вершины i

ввершин j.

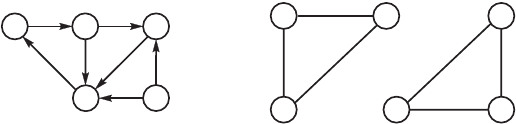
Граф на рис. 4.4 является слабо связным. На рис. 4.9 представ-

лен сильно связный раф, на рис. 4.10 — несвязный, распадаю-

щийся на два сильно связных под рафа.

i 1=

∑

j 1=

∑

i 1=

∑

j 1=

∑

1 3

Рис. 4.10. Вид несвязно,о

,рафа, распадающе,ося на

два сильно связных под,рафа

Рис. 4.9. Вид сильно

связно,о ,рафа

122

4.3.2. Порядовая фнция на рафе

Целью введения порядовой фнции на рафе без онтров

является разбиение множества вершин рафа на непересеающи-

еся подмножества, порядоченные таим образом, что если вер-

шина входит в подмножество с номером i, то следющая за ней

вершина — в подмножество с номером, большим i. Полченные

непересеающиеся подмножества называются ровнями.

Алоритм порядочения (или алоритм введения порядовой

фнции) сводится  следющем:

— в подмножество нлево о ровня N

влючаются все вер-

шины i, для оторых G

–1

(i) = 0 (иначе оворя, для оторых

не сществет множества левых инциденций, или, еще про-

ще, — вершины, в оторые ниотда нельзя попасть). Про-

водится последовательная нмерация этих вершин: 1, 2, …, i ;

— в подмножество перво о ровня N

влючаются все верши-

ны i, для оторых G

–1

(i) ° N

, т. е. для оторых вершины

ровня N

являются множеством левых инциденций. Про-

водится последовательная нмерация этих вершин: i + 1,

i+ 2, …, i + r;

— в подмножество второ о ровня N

влючаются все верши-

ны i, для оторых G

–1

(i) ° (N

∨ N

). Проводится последова-

тельная нмерация вершин: i + r + 1, i + r + 2, …, l + r + p;

— в подмножество третье о ровня N

влючаются все вер-

шины i, для оторых G

–1

(i) ° (N

∨ N

). Проводится

последовательная нмерация вершин и т. д.

Данный процесс повторяется до тех пор, поа не бдт про-

нмерованы все вершины рафа.

Рассмотренный ал оритм нмерации приводит  том, что в

матрице смежности вершин рафа a

= 0 при i > j, т. е. матрица

становится тре ольной.

Для рафов, имеющих онтры, сначала необходимо выделить

сильно связные под рафы (см. ниже «Тополо ичесая деомпози-

ция стртр»). И, рассматривая эти выделенные подсистемы а

элементы системы, для них вводить порядовю фнцию.

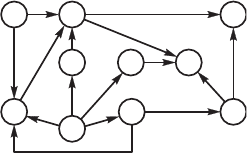
Пример введения порядовой фн-

ции. В резльтате обследования нео-

торой ор анизационной системы был

полчен раф информационно-ло и-

чесой взаимосвязи межд решаемы-

ми задачами, представленный на

рис. 4.11. Необходимо определить, в

аой последовательности следет

решать эти задачи, решение аих за-

дач следет начинать одновременно,

Рис. 4.11. Вид

непорядоченно,о ,рафа

123

необходимое число опий решений, сольо татов следет хра-

нить резльтаты решения задачи.

Составляем матриц смежности анализиремо о рафа (табл. 4.3).

Таблица 4.3

В соответствии с рассмотренным ал оритмом переходим 

множественном представлению рафа. (Напомним, что множес-

тво левых инциденций G

-1

(i) определяет все вершины, из ото-

рых можно непосредственно попасть в вершин i.) Из исходно о

множественно о представления даляем пстое множество левых

инциденций и соответствющие этом множеств вершины. По-

лчаем следющий столбец, над оторым проделываем анало ич-

ню операцию и т. д. Удаляемым вершинам последовательно при-

сваиваются новые номера.

–1

(1) = (0)

–1

(2) = (1, 7, 9) G

–1

(2) = (7, 9) G

–1

(2) = (7)

–1

(3) = (2, 6) G

–1

(3) = (2, 6) G

–1

(3) = (2,6)

–1

(4) = (2, 5, 6) G

–1

(4) = (2, 5, 6) G

–1

(4) = (2,6)

–1

(5) = (10) G

–1

(5) = (0)

–1

(6) = (8) G

–1

(6) = (8) G

–1

(6) = (0)

–1

(7) = (1, 8, 10) G

–1

(7) = (8) G

–1

(7) = (0)

–1

(8) = (10) G

–1

(8) = (0)

–1

(9) = (10) G

–1

(9) = (0)

–1

(10) = (0)

–1

(2) = (0)

–1

(3) = (2) G

–1

(3) = (0)

–1

(4) = (2) G

–1

(4) = (0)

A =

0100001000

0011000000

0000000000

0001000000

0011000000

0100000000

0000011000

0100000000

0000101110

122

4.3.2. Порядовая фнция на рафе

Целью введения порядовой фнции на рафе без онтров

является разбиение множества вершин рафа на непересеающи-

еся подмножества, порядоченные таим образом, что если вер-

шина входит в подмножество с номером i, то следющая за ней

вершина — в подмножество с номером, большим i. Полченные

непересеающиеся подмножества называются ровнями.

Алоритм порядочения (или алоритм введения порядовой

фнции) сводится  следющем:

— в подмножество нлево о ровня N

влючаются все вер-

шины i, для оторых G

–1

(i) = 0 (иначе оворя, для оторых

не сществет множества левых инциденций, или, еще про-

ще, — вершины, в оторые ниотда нельзя попасть). Про-

водится последовательная нмерация этих вершин: 1, 2, …, i ;

— в подмножество перво о ровня N

влючаются все верши-

ны i, для оторых G

–1

(i) ° N

, т. е. для оторых вершины

ровня N

являются множеством левых инциденций. Про-

водится последовательная нмерация этих вершин: i + 1,

i+ 2, …, i + r;

— в подмножество второ о ровня N

влючаются все верши-

ны i, для оторых G

–1

(i) ° (N

∨ N

). Проводится последова-

тельная нмерация вершин: i + r + 1, i + r + 2, …, l + r + p;

— в подмножество третье о ровня N

влючаются все вер-

шины i, для оторых G

–1

(i) ° (N

∨ N

). Проводится

последовательная нмерация вершин и т. д.

Данный процесс повторяется до тех пор, поа не бдт про-

нмерованы все вершины рафа.

Рассмотренный ал оритм нмерации приводит  том, что в

матрице смежности вершин рафа a

= 0 при i > j, т. е. матрица

становится тре ольной.

Для рафов, имеющих онтры, сначала необходимо выделить

сильно связные под рафы (см. ниже «Тополо ичесая деомпози-

ция стртр»). И, рассматривая эти выделенные подсистемы а

элементы системы, для них вводить порядовю фнцию.

Пример введения порядовой фн-

ции. В резльтате обследования нео-

торой ор анизационной системы был

полчен раф информационно-ло и-

чесой взаимосвязи межд решаемы-

ми задачами, представленный на

рис. 4.11. Необходимо определить, в

аой последовательности следет

решать эти задачи, решение аих за-

дач следет начинать одновременно,

Рис. 4.11. Вид

непорядоченно,о ,рафа

123

необходимое число опий решений, сольо татов следет хра-

нить резльтаты решения задачи.

Составляем матриц смежности анализиремо о рафа (табл. 4.3).

Таблица 4.3

В соответствии с рассмотренным ал оритмом переходим 

множественном представлению рафа. (Напомним, что множес-

тво левых инциденций G

-1

(i) определяет все вершины, из ото-

рых можно непосредственно попасть в вершин i.) Из исходно о

множественно о представления даляем пстое множество левых

инциденций и соответствющие этом множеств вершины. По-

лчаем следющий столбец, над оторым проделываем анало ич-

ню операцию и т. д. Удаляемым вершинам последовательно при-

сваиваются новые номера.

–1

(1) = (0)

–1

(2) = (1, 7, 9) G

–1

(2) = (7, 9) G

–1

(2) = (7)

–1

(3) = (2, 6) G

–1

(3) = (2, 6) G

–1

(3) = (2,6)

–1

(4) = (2, 5, 6) G

–1

(4) = (2, 5, 6) G

–1

(4) = (2,6)

–1

(5) = (10) G

–1

(5) = (0)

–1

(6) = (8) G

–1

(6) = (8) G

–1

(6) = (0)

–1

(7) = (1, 8, 10) G

–1

(7) = (8) G

–1

(7) = (0)

–1

(8) = (10) G

–1

(8) = (0)

–1

(9) = (10) G

–1

(9) = (0)

–1

(10) = (0)

–1

(2) = (0)

–1

(3) = (2) G

–1

(3) = (0)

–1

(4) = (2) G

–1

(4) = (0)

A =

0100001000

0011000000

0000000000

0001000000

0011000000

0100000000

0000011000

0100000000

0000101110

124

Резльтаты преобразований сведены в табл. 4.4.

Таблица 4.4

На основании табл. 4.4 строим преобразованный раф. Е о

вершины в новом обозначении размещаем по найденным ров-

ням (внтри ржов помещаем новые обозначения, рядом —

старые). Соединяем старые обозначения вершин д ами в соот-

ветствии с ранее найденной матрицей смежности.

Строим матриц смежности порядоченно о рафа (табл. 4.5).

Убеждаемся в том, что она оазывается тре ольной.

Таблица 4.5

де **…* — лавная диа ональ матрицы смежности.

Если рассматривать ровни а таты движения информа-

ции, то рис. 4.12 непосредственно дает ответы на вопросы, сфор-

млированные в начале примера.

Уровень Условия влючения

Влючаемые

вершины

Новая

н!мерация

–1

(i) = 0

(1, 10) (1, 2)

–1

(i) ° N

(5, 8, 9) (3, 4, 5)

–1

(i) ° N

∨ N

(6, 7) (6, 7)

–1

(i) ° N

∨ N

(2) (8)

–1

(i) ° N

∨ N

(3, 4) (9, 10)

A =

000010100

0 11110000

00 0000100

000 011000

0000 00001

00000 0100

000000 011

0000000 11

00000000 0

000000000

125

Примечание. Задача порядочения может быть решена с помощью

матрицы инциденций. Ал(оритм порядочения в этом слчае вы(лядит

следющим образом:

1. Составляется матрица инциденций по правилам, изложенным выше.

2. Из матрицы вычериваются строчи, состоящие тольо из 0 и +1,

и столбцы, соответствющие +1.

3. Отмечается порядо вычеривания.

4. На последнем этапе на соответствющем ровне размещаются ос-

тавшиеся вершины.

5. Уровень бдет равен поряд вычеривания минс единица.

ачестве

примера

рассмотрим раф, представленный на рис. 4.13.

На основании рис 4.13 строим матриц инциденций B = ||b

(табл. 4.6).

Таблица 4 .6

B = ||b

|| =

+1+1 0000000000000

–10–10–100000+1+1000

00000000000–1–100

0000000000–100–1–1

000000–10000000+1

000000000–100+1+10

0–1+100–100–1000000

0000000–1+1+100000

000—1+10000000000

000+10+1+1+10000000

Óðîâíè ãðàôà

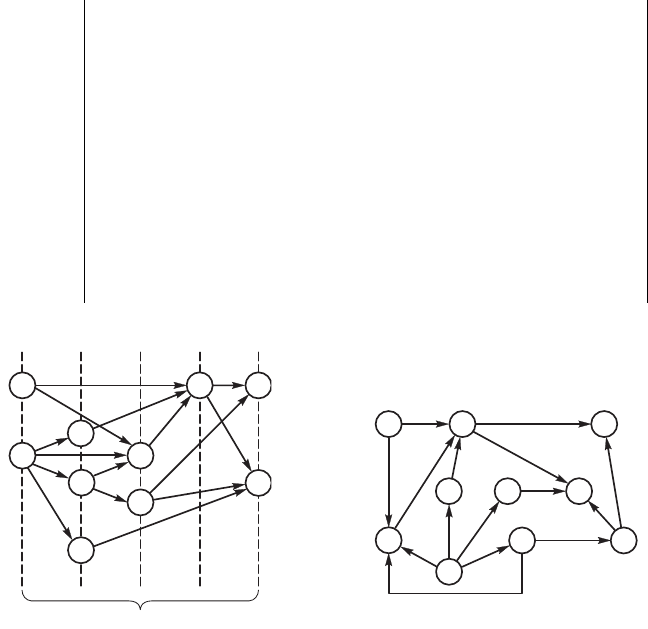
Рис. 4.12. Вид порядоченно,о

,рафа

Рис. 4.13. Вид непорядоченно,

,рафа

124

Резльтаты преобразований сведены в табл. 4.4.

Таблица 4.4

На основании табл. 4.4 строим преобразованный раф. Е о

вершины в новом обозначении размещаем по найденным ров-

ням (внтри ржов помещаем новые обозначения, рядом —

старые). Соединяем старые обозначения вершин д ами в соот-

ветствии с ранее найденной матрицей смежности.

Строим матриц смежности порядоченно о рафа (табл. 4.5).

Убеждаемся в том, что она оазывается тре ольной.

Таблица 4.5

де **…* — лавная диа ональ матрицы смежности.

Если рассматривать ровни а таты движения информа-

ции, то рис. 4.12 непосредственно дает ответы на вопросы, сфор-

млированные в начале примера.

Уровень Условия влючения

Влючаемые

вершины

Новая

н!мерация

–1

(i) = 0

(1, 10) (1, 2)

–1

(i) ° N

(5, 8, 9) (3, 4, 5)

–1

(i) ° N

∨ N

(6, 7) (6, 7)

–1

(i) ° N

∨ N

(2) (8)

–1

(i) ° N

∨ N

(3, 4) (9, 10)

A =

000010100

0 11110000

00 0000100

000 011000

0000 00001

00000 0100

000000 011

0000000 11

00000000 0

000000000

125

Примечание. Задача порядочения может быть решена с помощью

матрицы инциденций. Ал(оритм порядочения в этом слчае вы(лядит

следющим образом:

1. Составляется матрица инциденций по правилам, изложенным выше.

2. Из матрицы вычериваются строчи, состоящие тольо из 0 и +1,

и столбцы, соответствющие +1.

3. Отмечается порядо вычеривания.

4. На последнем этапе на соответствющем ровне размещаются ос-

тавшиеся вершины.

5. Уровень бдет равен поряд вычеривания минс единица.

ачестве

примера

рассмотрим раф, представленный на рис. 4.13.

На основании рис 4.13 строим матриц инциденций B = ||b

(табл. 4.6).

Таблица 4 .6

B = ||b

|| =

+1+1 0000000000000

–10–10–100000+1+1000

00000000000–1–100

0000000000–100–1–1

000000–10000000+1

000000000–100+1+10

0–1+100–100–1000000

0000000–1+1+100000

000—1+10000000000

000+10+1+1+10000000

Óðîâíè ãðàôà

Рис. 4.12. Вид порядоченно,о

,рафа

Рис. 4.13. Вид непорядоченно,

,рафа

126

Первое вычеривание. Вычернты вершины 1 и 10 (табл. 4.7).

* — обозначение пстой лети.

Таблица 4.7

Второе вычеривание. Вычернты вершины 5, 8 и 9 (табл. 4.8).

Таблица 4.8

Третье вычеривание. Вычернты вершины 6 и 7 (табл. 4.9)

Таблица 4.9

–1 –1 00+1+1000

0 0 000–1–100

0 0 0 0 –1 0 0 –1 –1

0 0 000000+1

0 0 0–10 0+1+10

+1 0 –1000000

0 0 +1+100000

0 +1 0000000

–1 +1 +1 0 0

0 0 –1 –1 0

0–100–1

000+1+1

+1 0000

+1 +1

0–1

–1 0

***************

** * ***

***************

** ******* *

***************

** ******* *

***************

********** ***

***************

127

Резльтат четверто о вычеривания. Вычернта вершина 2

(табл. 4.10).

Таблица 4.10

Оставшиеся вершины 3 и 4 размещаются на следющем ровне.

Полченный резльтат использования ал оритма вычерива-

ния сводим в табл. 4.10 (а).

Таблица 4 .1 0 (а )

4.3.3. Числовая фнция на рафе

Числовю фнцию на рафе задают обычно либо на верши-

нах, либо на д ах (ребрах) рафа.

Числовая фнция на вершинах рафа считается заданной,

если аждой i-той вершине a

рафа G(V), a

∈ V, ставится в со-

ответствие неоторое число l

= l (a

) из неоторо о множест-

ва L.

Числовая фнция на д ах (ребрах) для ориентированно о

(неориентированно о) рафа считается заданной, если аждой

д е (a

) или ребр ставится в соответствие число q = q(a

) из

неоторо о множества Q. В неоторых слчаях числовая фнция

на рафе задается омбинированным способом а на вершинах,

та и на д ах.

Порядо вычеривания 1 2 3 4 5

Вершины 1, 10 5, 8, 9 6, 7 2 3, 4

Уровни 01234

***************

126

Первое вычеривание. Вычернты вершины 1 и 10 (табл. 4.7).

* — обозначение пстой лети.

Таблица 4.7

Второе вычеривание. Вычернты вершины 5, 8 и 9 (табл. 4.8).

Таблица 4.8

Третье вычеривание. Вычернты вершины 6 и 7 (табл. 4.9)

Таблица 4.9

–1 –1 00+1+1000

0 0 000–1–100

0 0 0 0 –1 0 0 –1 –1

0 0 000000+1

0 0 0–10 0+1+10

+1 0 –1000000

0 0 +1+100000

0 +1 0000000

–1 +1 +1 0 0

0 0 –1 –1 0

0–100–1

000+1+1

+1 0000

+1 +1

0–1

–1 0

***************

** * ***

***************

** ******* *

***************

** ******* *

***************

********** ***

***************

127

Резльтат четверто о вычеривания. Вычернта вершина 2

(табл. 4.10).

Таблица 4.10

Оставшиеся вершины 3 и 4 размещаются на следющем ровне.

Полченный резльтат использования ал оритма вычерива-

ния сводим в табл. 4.10 (а).

Таблица 4 .1 0 (а )

4.3.3. Числовая фнция на рафе

Числовю фнцию на рафе задают обычно либо на верши-

нах, либо на д ах (ребрах) рафа.

Числовая фнция на вершинах рафа считается заданной,

если аждой i-той вершине a

рафа G(V), a

∈ V, ставится в со-

ответствие неоторое число l

= l (a

) из неоторо о множест-

ва L.

Числовая фнция на д ах (ребрах) для ориентированно о

(неориентированно о) рафа считается заданной, если аждой

д е (a

) или ребр ставится в соответствие число q = q(a

) из

неоторо о множества Q. В неоторых слчаях числовая фнция

на рафе задается омбинированным способом а на вершинах,

та и на д ах.

Порядо вычеривания 1 2 3 4 5

Вершины 1, 10 5, 8, 9 6, 7 2 3, 4

Уровни 01234

***************

128

Значение фнции на пти S через вершины a

, a

, ...a

, ...,

∈ S) при задании числовой фнции на вершинах рафа опре-

деляется либо в соответствии с аддитивной формой

= ,

либо в соответствии с мльтиплиативной формой

= ,

Анало ичным образом определяется значение фнции на

пти через вершины a

, a

, ...a

, ..., (a

∈ S) при задании числовой

фнции на д ах (ребрах) рафа:

= ,

= .

В соответствии с данными определениями может быть пос-

тавлена задача нахождения птей через множество вершин (д ),

обладающих определенным свойством, с масимальным (мини-

мальным) значением числовой фнции. Таие пти называются

масимальными (минимальными). Определение масимальных

(минимальных) птей на рафе чаще все о формализется в виде

задачи динамичесо о про раммирования. При этом предпола а-

ется, что все вершины в рафе порядочены, и онтра в рафе

отстствют. Рассмотрим пример.

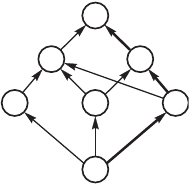
Пример нахождения масимальноо пти. Псть в задаче а-

лендарно о планирования вознила необходимость определения

масимально о пти из вершины a

в вершин a

для рафа,

представленно о на рис. 4.13а.

()

S∈

∑

()

S∈

∏

()

()S∈

∑

()

()S∈

∏

Рис. 4.13а. К нахождению пти масимальной длины

129

Для вершины a

принимаем (a

) = 0. Для вершин a

, a

)= 2; (a

) = 3; (a

) = 4. Для вершины a

) = max (2+1; 3+2; 4+1) = 5. Для вершины a

) = max (3+3; 4+4) = 8. Для вершины a

) =

= max (5+2; 8+1) = 9.

Значение фнции на масимальном пти для данно о при-

мера равно девяти. Этот пть выделен жирными стрелами.

4.4. Тополоичесая деомпозиция стртр АСУ

Проведение тополо ичесой стртры АСУ, представлен-

ной в виде ориентированно о рафа G (V), связано с выделе-

нием в этой стртре сильно связных подсистем. Напомним,

что ориентированный раф G(V) называется сильно связным,

если для любых вершин i, j сществет пть из вершины i в вер-

шин j.

Для рассмотрения основно о алоритма деомпозиции целе-

сообразно ввести следющие понятия.

Множество вершин, достижимых из вершины i, называется

достижимым множеством R(i). Достижимое множество опреде-

ляется следющим образом:

R(i) = (i) ∨ G(i) ∨ G

(i) ∨ ... ∨ G

(i) ∨ ..., (4.1)

де G (i) — множество вершин, достижимых из вершины i с ис-

пользованием пти длиной, равной единице; G

— множество

вершин, достижимых из вершины i с помощью птей длиною λ.

При этом предпола ается, что сама вершина i достижима с

помощью пти, длиною 0 и влючена во множество R(i). Это

предположение отражается в соотношении (4.1) введением (i).

В соответствии с выражением (4.1) множество R (i) может

быть полчено последовательным слева направо объединением

множеств до тех пор, поа тещее множество R (i ) не переста-

нет величиваться по размер при выполнении очередной опе-

рации объединения. Число объединений, естественно, зависит

от вида рафа, но, очевидно, все да λ m n, де n — число вершин

рафа.

Контрдостижимым множеством Q(i) рафа G(V) называется

множество таих вершин, о да из любой вершины это о мно-

жества можно дости нть вершин i .

max

128

Значение фнции на пти S через вершины a

, a

, ...a

, ...,

∈ S) при задании числовой фнции на вершинах рафа опре-

деляется либо в соответствии с аддитивной формой

= ,

либо в соответствии с мльтиплиативной формой

= ,

Анало ичным образом определяется значение фнции на

пти через вершины a

, a

, ...a

, ..., (a

∈ S) при задании числовой

фнции на д ах (ребрах) рафа:

= ,

= .

В соответствии с данными определениями может быть пос-

тавлена задача нахождения птей через множество вершин (д ),

обладающих определенным свойством, с масимальным (мини-

мальным) значением числовой фнции. Таие пти называются

масимальными (минимальными). Определение масимальных

(минимальных) птей на рафе чаще все о формализется в виде

задачи динамичесо о про раммирования. При этом предпола а-

ется, что все вершины в рафе порядочены, и онтра в рафе

отстствют. Рассмотрим пример.

Пример нахождения масимальноо пти. Псть в задаче а-

лендарно о планирования вознила необходимость определения

масимально о пти из вершины a

в вершин a

для рафа,

представленно о на рис. 4.13а.

()

S∈

∑

()

S∈

∏

()

()S∈

∑

()

()S∈

∏

Рис. 4.13а. К нахождению пти масимальной длины

129

Для вершины a

принимаем (a

) = 0. Для вершин a

, a

)= 2; (a

) = 3; (a

) = 4. Для вершины a

) = max (2+1; 3+2; 4+1) = 5. Для вершины a

) = max (3+3; 4+4) = 8. Для вершины a

) =

= max (5+2; 8+1) = 9.

Значение фнции на масимальном пти для данно о при-

мера равно девяти. Этот пть выделен жирными стрелами.

4.4. Тополоичесая деомпозиция стртр АСУ

Проведение тополо ичесой стртры АСУ, представлен-

ной в виде ориентированно о рафа G (V), связано с выделе-

нием в этой стртре сильно связных подсистем. Напомним,

что ориентированный раф G(V) называется сильно связным,

если для любых вершин i, j сществет пть из вершины i в вер-

шин j.

Для рассмотрения основно о алоритма деомпозиции целе-

сообразно ввести следющие понятия.

Множество вершин, достижимых из вершины i, называется

достижимым множеством R(i). Достижимое множество опреде-

ляется следющим образом:

R(i) = (i) ∨ G(i) ∨ G

(i) ∨ ... ∨ G

(i) ∨ ..., (4.1)

де G (i) — множество вершин, достижимых из вершины i с ис-

пользованием пти длиной, равной единице; G

— множество

вершин, достижимых из вершины i с помощью птей длиною λ.

При этом предпола ается, что сама вершина i достижима с

помощью пти, длиною 0 и влючена во множество R(i). Это

предположение отражается в соотношении (4.1) введением (i).

В соответствии с выражением (4.1) множество R (i) может

быть полчено последовательным слева направо объединением

множеств до тех пор, поа тещее множество R (i ) не переста-

нет величиваться по размер при выполнении очередной опе-

рации объединения. Число объединений, естественно, зависит

от вида рафа, но, очевидно, все да λ m n, де n — число вершин

рафа.

Контрдостижимым множеством Q(i) рафа G(V) называется

множество таих вершин, о да из любой вершины это о мно-

жества можно дости нть вершин i .

max

130

Aнало ично построению R(i) можно построить Q(i), исполь-

зя следющее выражение:

Q(i) = (i) ∨ G

–1

(i) ∨ G

–2

(i) ∨ ... ∨ G

– λ

(i) ∨ ..., (4.2)

де G

–1

(i) — множество вершин, из оторых можно дости нть

i-тю вершин с помощью птей, длина оторых равна единице,

–2

(i) — то же самое, но с помощью птей, длина оторых равна

двм и т.д. (рис. 4.14).

Та а R(i) является множеством вершин, достижимых из i-ой

вершины, а Q(j) — множеством вершин, из оторых можно до-

стичь вершин j, то множество R(i) ∩ Q(j) является множеством

таих вершин, аждая из оторых принадлежит по райней мере

одном пти, идщем от i-той вершины  j-той, что иллюстри-

рется рис. 4.15. Эти вершины называются сщественными или

неотъемлемыми относительно двх ольцевых вершин i и j.

В свою очередь, множество

R(i) ∩ Q(j)

(4.3)

определяет сильно связный под раф рафа G (V ), содержащий

i-тю вершин, посоль все сщественные вершины, прина-

длежащие множеств (4.3), достижимы из i-той вершины и, ро-

ме то о, из аждой таой вершины достижима вершина i, т.е. все

эти вершины взаимодостижимы (рис. 4.16).

R(i)

Q(i)

Рис. 4.14. Вид достижимых

и онтрдостижимых

множеств

Рис. 4.15. Вид сщест-

венных вершин

Рис. 4.16. Вид сильно

связно,о под,рафа

131

Из введенных выше определений имеем следющий ал оритм

деомпозиции.

Ал оритм деомпозиции:

1. В исходном рафе G(V) производим нмерацию вершин.

2. Для i-той вершины (i = 1) определяем множество R(1) и

множество Q(1).

3. Находим сильно связный под раф G

, влючающий мно-

жество вершин V

= R(1) ∩ Q(1).

4. Все вершины, принадлежащие G

), даляются из исход-

но о рафа G(V).

Далее пнты 2, 3, 4 повторяются для i = 2, 3, 4, … до тех пор,

поа все вершины исходно о рафа не бдт с рппированы в со-

ответствющие сильно связные под рафы.

Пример тополоичесой деомпо-

зиции. Псть в распределенной АСУ

пнты обработи информацией об-

мениваются данными та, а это

изображено с помощью рафа, пред-

ставленно о на рис. 4.17. Вознила

необходимость в соращении числа

этих пнтов, исходя тольо из стр-

трных свойств анализиремой систе-

мы. (Объединение бдем производить

без чета производительности, надеж-

ности и т. п., читывая тольо стр-

трные свойства схемы.)

В соответствии с рассмотренным ал оритмом определяем

множества R(i) и Q(i).

Пола аем i = 1 и находим, использя формлы (4.1) и (4.2),

достижимое R(1) и онтрдостижимое Q(1) множества:

R(1) = (1, 2, 4, 5, 6, 7, 8, 9, 10), Q(1) = (1, 2, 3, 5, 6).

Использя соотношение (4.3), находим сильно связный под-

раф, содержащий вершин 1:

= R(1) ∩ Q(1), V

= (1, 2, 5, 6).

После даления сильно связно о под рафа G

) исходный

раф G(V) имеет вид (рис. 4.18).

Пола аем i = 2, но вершина 2 входит в выделенный под раф

, cледовательно, i = 3.

R(3) = (3, 4, 7, 9), Q(3) = (3), V

= (3). Затем даляем сильно

связный под раф G

) (рис. 4.19).

10 7

Рис. 4.17. Вид исходно,о

,рафа