Мазалов В.В. (ред.) - Математические методы в экологии. Тезисы докладов Третьей Всероссийской школы молодых ученых
Подождите немного. Документ загружается.


2 3
2
2 3

P
P
P
P
P
P
−1
∆
C P
−1
L P
−1
)
P
−1
P
P
−1
)
L
−1
) C
P
L.
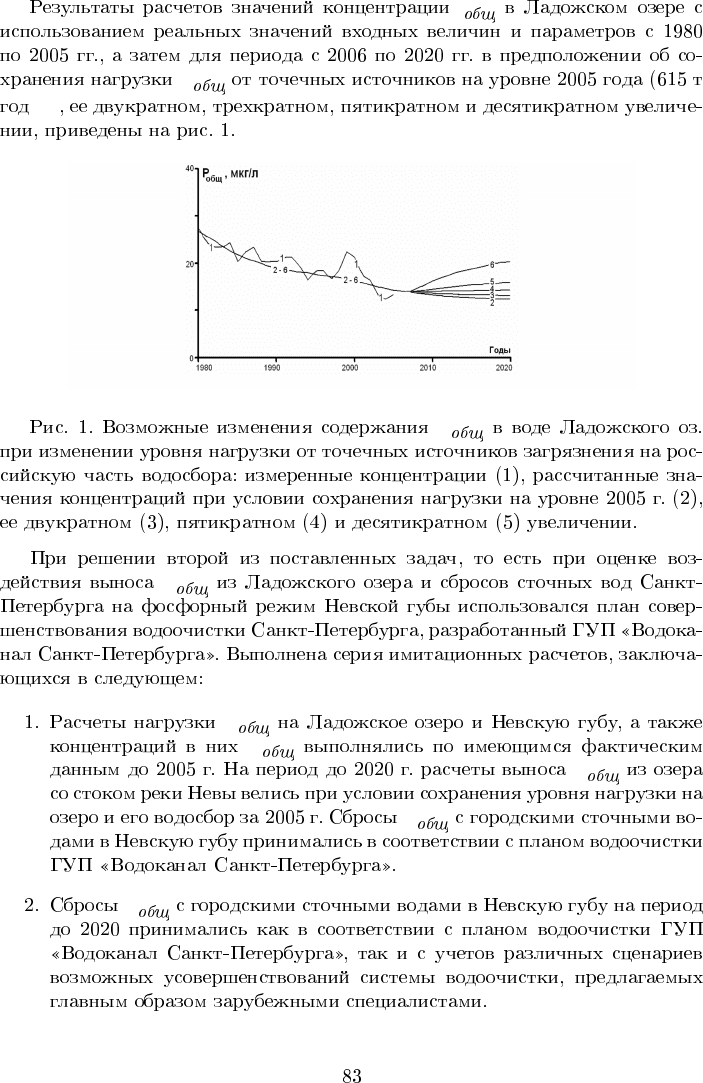
P
P
−1
)
P
P
P
P
P
P
P

P
P
P
−1
P
−1
P
−
1
P
P
−1
−1
−1
P
−1
P
−1

−1
−1
−3
−3

∂c
∂t
= D
∂
2
c
∂x
2
, t > 0, x ∈ (0, `), c(0, x) = ϕ(x), x ∈ [0, ` ],
D
∂c
∂x
¯
¯
¯
x=0
= bc
2
0
, D
∂c
∂x
¯
¯
¯
x=`
= −bc
2
`
, c
0
(t) ≡ c(t, 0), c
`
(t) ≡ c(t, `).
c(t, x)
D b
H
D b T
D(T ) = D
0
exp{−E
D
/[RT ]} b(T ) = b
0
exp{−E
b
/[RT ]}
D
0
, b
0
, E
D
, E
b
= const
ϕ(x) = ¯c
ϕ(x) = ¯c − A(x − `/2)
2
, A > 0. A
J(t) = bc
2
0
(t) = bc
2
`
(t)
[0, t
∗
] J(t
∗
) ≈ 0
J(t)

y = f(˜a, x),
x = (x
1
, ..., x
n
) x
i
∈ X, i = 1, ..., n
X ˜a = (˜a
1
, ..., ˜a
n
)
˜a
i
˜a
i
= [a
i1
, a
i2
]
x, x ∈ X
˜y = f(˜a, x) x
∗
, x
∗
∈ X
˜y = f(˜a, x
∗
)
X
∨ = max ∧ = min
˜a ∨
˜
b = {a ∨ b|a ∈ ˜a, b ∈
˜
b}, ˜a ∧
˜
b = {a ∧ b|a ∈ ˜a, b ∈
˜
b},
˜a
˜
b

(˜a >
˜
b) ⇔ (˜a ∨
˜
b = ˜a, ˜a ∧
˜
b =
˜
b)
˜a
˜
b ˜a >
˜
b
˜
b > ˜a
≥ ˜a
˜
b
˜a
k
, k = 1, ..., n ˜a
1
˜a
2
, ..., ˜a
k
> ˜a
1
> ˜a
2
, ..., ˜a
1
> ˜a
k
(˜a
1
6 ˜a
2
, ..., ˜a
1
6 ˜a
k
)
˜a = [a
1
, a
2
]
˜
b = [b
1
, b
2
]
˜a >
˜
b
(a
1
> b
1
, a
2
> b
2
) (a
1
< b
1
, a
2
> b
2
)
(b
1
< a
1
, b
2
> a
2
))
˜a
k
= [a
k1
, a
k2
],
k = 1, ..., n ˜a
1
a
11
=
n
_
k=1
a
k1,
a
12
=
n
_
k=1
a
k2
,
˜a
1
a
11
=
n
^
k=1
a
k1,
a
12
=
n
^
k=1
a
k2
.


ax
x+x
0
a
x
0
x
