Maxima - руководство на русском языке

Подождите немного. Документ загружается.

MAXIMA: РУКОВОДСТВО

Вольный перевод (не оконч.): Сологаев Валерий Иванович, 26 апреля 2009 г.

http://sologaev2010.narod.ru (на примере maxima и wxmaxima)

Maxima - система компьютерной алгебры, осуществленная на языке Lisp.

Maxima происходит из системы Macsyma, развивавшейся в MIT в 1968 - 1982 годах

как часть Проекта МАКИНТОША. MIT передал копию исходного текста Macsyma

Министерству энергетики в 1982; та версия теперь известна как DOE Macsyma. Копия DOE

Macsyma поддерживалась Уильямом Ф. Шелтером, профессором Университета Техаса с

1982 года до его смерти в 2001. В 1998 Шелтер получил разрешение от Министерства

энергетики, чтобы открыть исходные тексты DOE Macsyma согласно Лицензии GNU и в

2000 он начал проект свободной Maxima в SourceForge, чтобы поддержать и развить DOE

Macsyma, теперь названный Maxima.

1. Введение в Maxima

Стартуют Maxima командами "maxima" (в консоли) или "wxmaxima" (графическая

оболочка с виджетами). В начале Maxima показывает информацию о версии и приглашение

командной строки. В конце каждой команды Maxima надо ставить точку с запятой ";".

Завершают сессию Maxima командой "quit();". Пример работы Maxima показан в

графической среде wxMaxima операционной системы (ОС) Linux Debian 5.0:

(%i1) factor(10!);

(%o1)

(%i2) expand ((x + y)^6);

(%o2)

6xy

15x

20x

15x

6x

yx

(%i3) factor (x^6 – 1);

(%o3)

 x−1∗ x1∗ x

−x1∗x

x1

Чтобы использовать результат из предыдущих вычислений, можно назначить его

переменной или обратиться по метке типа %o2. Кроме того, встроенная метка % отсылает к

последнему расчетному результату, например:

(%i1) u: expand ((x + y)^6);

(%o1)

6∗x∗ y

15∗x

∗y

20∗x

∗ y

15∗x

∗ y

6∗x

∗y x

(%i2) diff (u, x);

(%o2)

6∗y

30∗x∗y

60∗x

∗ y

60∗x

∗y

30∗x

∗y6∗x

(%i3) factor (%o2);

(%o3)

6∗ yx 

или так (результат тот же):

(%i3) factor (%);

(%o3)

6∗ yx 

Maxima может работать с комплексными числами и числовыми константами:

(%i1) cos(%pi);

(%o1) -1

(%i2) exp(%i*%pi);

(%o2) -1

Maxima может выполнять дифференциальные и интегральные вычисления:

(%i1) u: expand ((x + y)^6);

(%o1)

6∗x∗ y

15∗x

∗y

20∗x

∗ y

15∗x

∗ y

6∗x

∗yx

(%i2) diff (%, x);

(%o2)

6∗y

30∗x∗y

60∗x

∗ y

60∗x

∗y

30∗x

∗y6∗x

(%i3) integrate (1/(1 + x^3), x);

(%o3)

−log x

−x1/6atan 2∗x−1/



3/



3log x 1/3

Maxima может решать линейные системы и кубические уравнения:

(%i1) linsolve ([3*x + 4*y = 7, 2*x + a*y = 13], [x, y]);

(%o1)

[x=7∗a−52/3∗a−8 , y=25/3∗a−8]

(%i2) solve (x^3 - 3*x^2 + 5*x = 15, x);

(%o2)

[x=−



5∗i , x=



5∗i , x=3]

Maxima может решать нелинейные системы уравнений. Заметьте, что, если Вы не

хотите выводить на экран результат, Вы можете закончить вашу команду знаком доллара

"$" вместо точки с запятой ";":

(%i1) eq_1: x^2 + 3*x*y + y^2 = 0$

(%i2) eq_2: 3*x + y = 1$

(%i3) solve ([eq_1, eq_2]); /* переменные x и y */

(%o3)

[ [ y=−3∗



57/ 2, x=



5 3/2] ,[ y=3∗



5−7/ 2, x=−



5−3/ 2]]

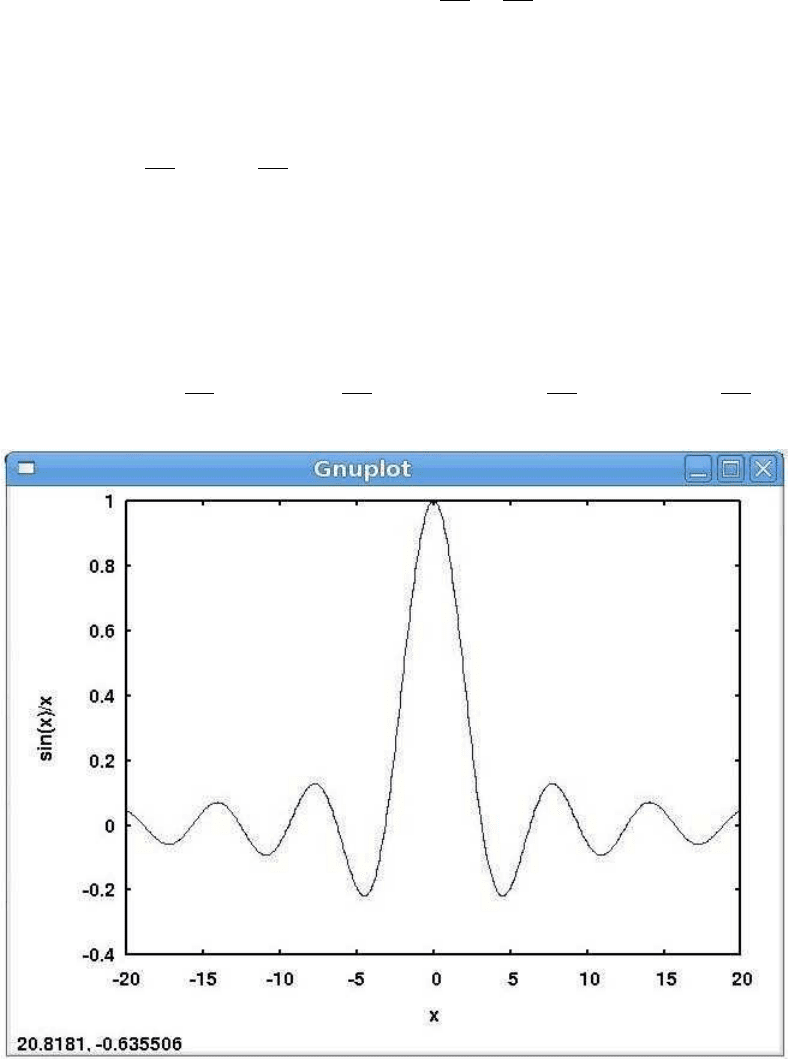
Рис. 1

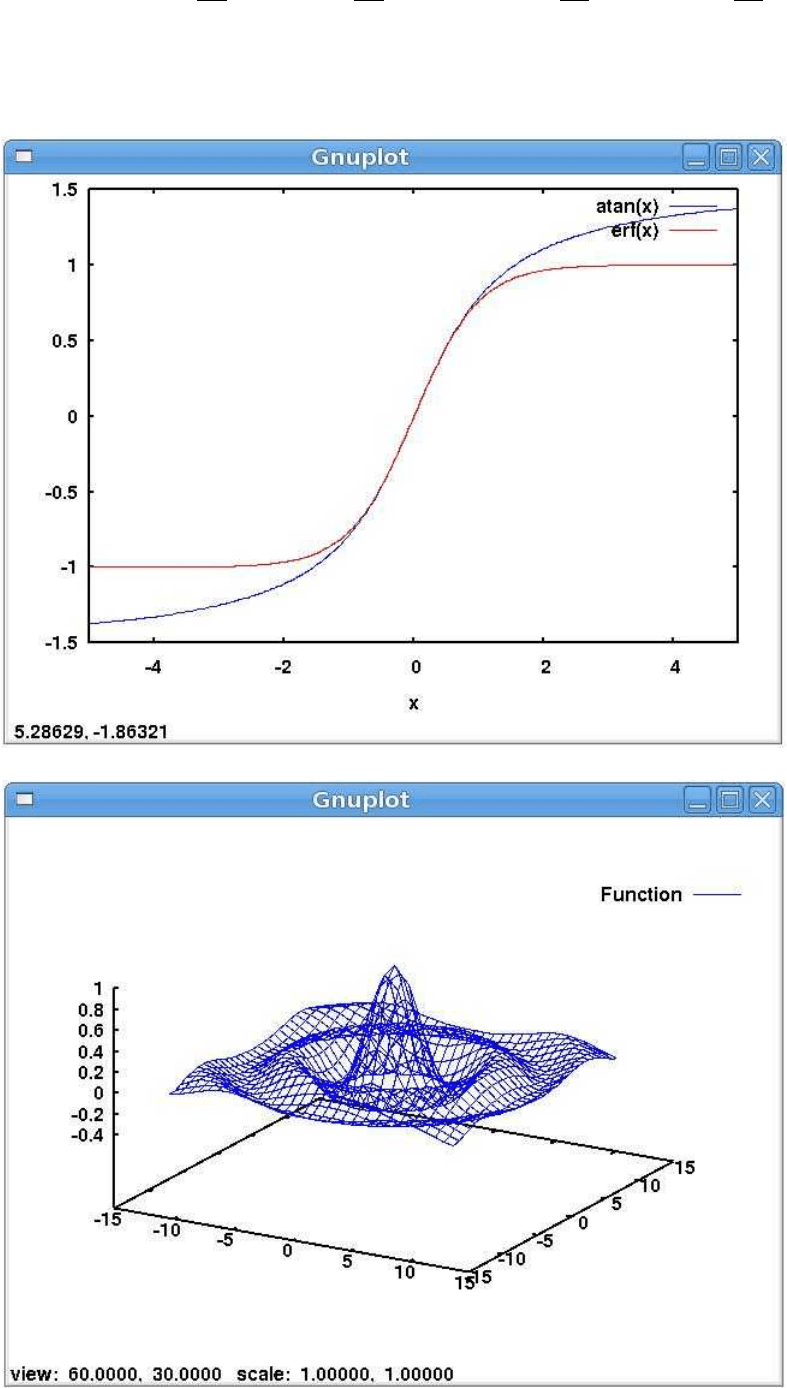
Maxima может строить графики из одной или нескольких функций (рис. 1, 2, 3):

(%i1) eq_1: x^2 + 3*x*y + y^2 = 0$

(%i2) eq_2: 3*x + y = 1$

(%i3) solve ([eq_1, eq_2]);

(%o3)

[ [ y=−3∗



57/ 2, x=



5 3/2] ,[ y=3∗



5−7/ 2, x=−



5−3/ 2]]

(%i4) kill(labels);

(%o0) done

(%i1) plot2d (sin(x)/x, [x, -20, 20]); /* рис. 1 (комментарий как в Си)*/

Рис. 2

Рис. 3

(%i2) plot2d ([atan(x), erf(x), tanh(x)], [x, -5, 5]); /* рис. 2 */

(%o2)

(%i3) plot3d (sin(sqrt(x^2 + y^2))/sqrt(x^2 + y^2), [x, -12, 12],

[y,-12, 12]); /* рис. 3 (комментарий как в Си)*/

(%o3)

2. Lisp и Maxima

Maxima написана на Lisp и имеет легкий доступ к Lisp-функциям и переменным из

Maxima и наоборот. Символы Lisp и Maxima отличаются соглашением обозначений имён.

Символ Lisp начинается с долларового знака $ и это соответствует символу Maxima без

долларового знака. Символ Maxima, который начинается с вопросительного знака ?,

соответствует Lisp-символу без вопросительного знака. Например, символ Maxima foo

соответствует Lisp-символу $foo, в то время как символ Maxima ?foo соответствует Lisp

символу foo. Заметьте, что ?foo написан без пробела между ? и foo, иначе это могло

бы быть ошибкой.

Дефис -, звездочка * или другие специальные символы Lisp нужно экранировать

наклонной чертой влево \ там, где они появляются в коде Maxima. Например, Lisp-

идентификатор *foo-bar* пишут как ?\*foo\-bar\* в Maxima.

Lisp-код может быть выполнен внутри сессии Maxima. Отдельная строка Lisp

(содержащая одну или более форм), может быть выполнена специальной командой

:lisp. Например,

(%i1) :lisp (foo $x $y)

вызывает Lisp-функцию foo с переменными Maxima x и y как аргументами. Конструкция

:lisp может появиться в командной строке или в файле, обработанными командами

batch или demo, но не в файле, обработанном командами load, batchload,

translate_file, или compile_file.

Функция to_lisp() открывает интерактивную Lisp-сессию. Ввод (to-maxima)

закрывает Lisp-сессию и возвращает в Maxima.

Lisp-функции и переменные, которые могут быть видимы в Maxima как функции и

переменные с обычными именами (без специальной пунктуации), должны иметь в начале

Lisp-имени знак доллара $.

Maxima регистрозависимая, то есть различаются строчные и прописные буквы в

идентификаторах, а в Lisp этого нет, не регистрозависим Lisp.

Три правила трансляции имён между Lisp и Maxima таковы:

1. Идентификатор Lisp, не распоженный между вертикальными скобками |...|,

соответствует идентификатору Maxima в строчных буквах. Является ли Lisp-

идентификатор заглавным, строчным, или смешанным случаем, игнорируется. Например,

в Lisp $foo, $FOO и $Foo одинаково соответствуют Maxima-идентификатору foo.

2. Идентификатор Lisp, который состоит весь из прописных букв, или весь из

строчных букв и распоженный между вертикальным скобками |...|, соответствует

Maxima-идентификатору с противоположным регистром. Таким образом, прописные

буквы замененяются на строчные буквы и строчные буквы на прописные буквы.

Например, в Lisp, |$FOO | и |$foo | соответствуют в Maxima foo и FOO,

соответственно.

3. Lisp-идентификатор, в котором смешаны прописные буквы и строчные буквы,

расположенный между вертикальными скобками |...|, соответствует идентификатору

Maxima с тем же самым случаем. Например, в Lisp, |$Foo | соответствует в Maxima Foo.

Lisp #$макрос позволяет использовать выражения Maxima в Lisp-коде. #$expr$

расширяется в Lisp выражение, эквивалентное выражению Maxima expr. Например, с

помощью Lisp так:

(msetq $foo #$[x, y]$)

Это экивавалентно в Maxima команде:

(%i1) foo: [x, y];

Lisp-функция displa выводит выражение в формате Maxima.

Далее не будем углубляться в Lisp, так как наша цель – Maxima!

3. Garbage Collection (Собирание мусора)

Символические вычисления имеют тенденцию создавать много мусора (в памяти) .

Эффективная обработка этого может стать критической для успешного завершения

некоторых программ. Но в UNIX-системах сборка мусора производится автоматически.

4. Функции и переменные Maxima для Help

Функция: demo (filename)

Вычисляет Maxima-выражение в файле с именем filename и выводит на экран

результаты. Функция demo делает паузу после вычислений каждого выражения и

продолжает вычисления после того, как пользователь нажмёт ENTER.

Функция demo ищет в списке директорий file_search_demo файл filename. Если

файл имеет суффикс (расширение) dem, то суффикс может быть опущен. Смотри также

file_search.

Функция demo вычисляет свои аргументы. Функция demo возвращает имя

демонстрационного файла.

Функция: example (topic)

Функция: example ()

Функция example (topic) выводит на экран несколько примеров по ключевому

слову topic. Функция example () возвращает список всех связанных тем. Примеры:

(%i1) example (append);

(%i1)

(%i2) append([x+y,0,-3.2],[2.5E+20,x])

(%o2)

[ yx ,0 ,−3.2 ,2.5∗10

20,

(%o2) done

(%i3) example (coeff);

(%i1)

(%i4) coeff(b+tan(x)+2*a*tan(x) = 3+5*tan(x),tan(x))

(%o4) 2*a+1=5

(%i1)

(%i5) coeff(1+x*%e^x+y,x,0)

(%o5) y+1

(%o5) done

5. Командная строка Maxima

Оператор ' предотвращает вычисление выражения Maxima.

Применительно к вызову функции одиночная кавычка ' предотвращает вычисление

вызываемой функции, однако аргументы функции вычисляются. Результат получается в

форме существительного (noun) функции.

Применительно к выражению, заключённому в скобки, одиночная кавычка '

предотвращает вычисление ВСЕХ вызываемых символов и функций в выражении.

Например, при '(f(x)) не вычисляется выражение f(x). Однако, если набрано 'f(x)

(с одиночной кавычкой применительно лишь к f вместо всего f(x)), то возвращается

форма существительного (noun) f по [x].

Одиночная кавычка ' не предотвращает simplification-упрощение.

Когда глобальный флаг noundisp включён, на экран выводятся nouns-

существительные с одиночной кавычкой. Этот переключатель всегда включён, когда

выводятся на экран определения функции.

Примеры (применительно к символу):

(%i1) aa: 1024;

(%o1)

1024

(%i2) aa^2;

(%o2)

1048576

(%i3) 'aa^2;

(%o3)

(%i4) ''%;

(%o4)

1048576

Примеры (применительно к функции):

(%i1) x0: 5;

(%o1)

(%i2) x1: 7;

(%o2)

(%i3) integrate (x^2, x, x0, x1);

(%o3)

218/3

(%i4) 'integrate (x^2, x, x0, x1);

(%o4)

∫

(%i5) %, nouns;

(%o5)

218/3

Примеры (применительно к выражению в скобках):

(%i1) aa: 1024;

(%o1)

1024

(%i2) bb: 19;

(%o2)

(%i3) sqrt(aa) + bb;

(%o3)

(%i4) '(sqrt(aa) + bb);

(%o4)

bb



aa

(%i5) ''%;

(%o5)

Примеры (одиночная кавычка не предотвращает упрощение выражения):

(%i1) sin(17*%pi)+cos(17*%pi);

(%o1)

−1

(%i2) '(sin(17*%pi)+cos(17*%pi));

(%o2)

−1

Оператор: '' (две одиночных кавычки)

Оператор из двух одиночных кавычек '' преобразует вычисления в input

выражения (действие, противоположное оператору одиночной кавычки ').

Расширенный пример:

(%i1) expand ((a + b)^3);

(%o1)

3∗a∗b

3∗a

∗ba

(%i2) [_, ''_];

(%o2)

[expand ba

 , b

3∗a∗b

3∗a

∗ba

]

(%i3) [%i1, ''%i1];

(%o3)

[expand ba

 , b

3∗a∗b

3∗a

∗ba

]

(%i4) [aa : cc, bb : dd, cc : 17, dd : 29];

(%o4)

[cc ,dd ,17,29]

(%i5) foo_1 (x) := aa - bb * x;

(%o5)

foo

 x:=aa−bb∗x

(%i6) foo_1 (10);

(%o6)

cc−10∗dd

(%i7) ''%;

(%o7)

−273

(%i8) ''(foo_1 (10));

(%o8)

−273

(%i9) foo_2 (x) := ''aa - ''bb * x;

(%o9)

foo

 x :=cc−dd∗x

(%i10) foo_2 (10);

(%o10)

−273

(%i11) [x0 : x1, x1 : x2, x2 : x3];

(%o11)

[x1 , x2 , x3]

(%i12) x0;

(%o12)

(%i13) ''x0;

(%o13)

(%i14) '' ''x0;

(%o14)

При использовании оператора двух одинарных кавычек '' в выражении, оператор

меняет noun-существительное на verb-глагол (если это уже не verb-глагол). Примеры:

(%i1) sin (1);

(%o1)

sin 1

(%i2) ''sin (1);

(%o2)

0.8414709848079

(%i3) declare (foo, noun);

(%o3)

done

(%i4) foo (x) := x - 1729;

(%o4)

foo  x:=x−1729

(%i5) foo (100);

(%o5)

foo 100

(%i6) ''foo (100);

(%o6)

−1629

Оператор '' применяет parser-анализатор input-входа; это не сохраняется как часть

разобранного input-входного выражения. Пример:

(%i1) [aa : bb, cc : dd, bb : 1234, dd : 5678];

(%o1)

[bb , dd ,1234 ,5678]

(%i2) aa + cc;

(%o2)

dd bb

(%i3) display(_,op(_),args (_));_=cc+aaop(cc+aa)=+args(cc+aa)=[cc,aa]

(%o3)

done

(%i4) ''(aa + cc);

(%o4)

6912

(%i5) display (_, op(_),args (_));_=dd+bbop(dd+bb)=+args(dd+bb)=[dd,bb]

(%o5)

done

Две одиночных кавычки '' вызывают вычисление, когда вычисление подавлено,

как в определениях функции, лямбда выражениях, так и в выражениях, указанных

одиночной кавычкой '. Например

(%i1) foo_1a (x) := ''(integrate (log (x), x));

(%o1) foo_1a(x):=x*log(x)-x

(%i2) foo_1b (x) := integrate (log (x), x);

(%o2) foo_1b(x):=integrate(log(x),x)

(%i3) dispfun (foo_1a, foo_1b);

(%t3) foo_1a(x):=x*log(x)-x

(%t4) foo_1b(x):=integrate(log(x),x)

(%o4) [%t3,%t4]

(%i5) foo_2a (x) := ''%;

(%o5) foo_2a(x):=[%t3,%t4]

(%i6) foo_2b (x) := %;

(%o6) foo_2b(x):=%

(%i7) dispfun (foo_2a, foo_2b);

(%t7) foo_2a(x):=[%t3,%t4]

(%t8) foo_2b(x):=%

(%o8) [%t7,%t8]

(%i9) F : lambda ([u], diff (sin (u), u));

(%o9) lambda([u],diff(sin(u),u))

(%i10) '(sum (a[k], k, 1, 3) + sum (b[k], k, 1, 3));

(%o10) sum(b[k],k,1,3)+sum(a[k],k,1,3)

(%i11) '(''(sum (a[k], k, 1, 3)) + ''(sum (b[k], k, 1, 3)));

(%o11) b[3]+a[3]+b[2]+a[2]+b[1]+a[1]

6. Функции и переменные для командной строки

Функция: alias (new_name_1, old_name_1, ..., new_name_n, old_name_n)

Обеспечивает альтернативное имя для (пользовательской или системной) функции,

переменной, массива и др. Некоторые номера аргументов могут быть использованы.

Функция: ev (expr, arg_1, ..., arg_n)

Вычисляет выражение expr в окружении специфицированных аргументов

arg_1, ..., arg_n. Аргументами могут быть switches-ключи (Булёвые флаги),

присвоения, уравнения и функции. Функция ev возвращает результат (другое выражение)

после вычислений.

Вычисление функции ev выполняется пошагово в таком порядке:

1. Сперва устанавливаются аргументы, которые могут быть некоторые или все из

нижеперечисленных:

а) simp заставляет выражение expr упроститься независимо от установок ключей

simp, которые запрещают упрощение если ложно.

б) noeval подавляет фазу вычисления ev (см. шаг (4) ниже). Это полезно в

соединении с другими выключателями и при выполнении expr, чтобы быть повторно

упрощенным без того, чтобы быть перевычисленным.

в) nouns-существительные вызывают вычисление форм существительного (типично

невычисленные функции, типа 'integrate или 'diff) в выражении expr.

г) expand-расширение интенсифицируется.

д) expand (m, n) выполняется, устанавливая значения maxposex и maxnegex в m

и n соответственно.

е) detout заставляет любые матричные инверсии, вычисленные в expr, иметь

детерминант, сохраненный вне инверсии вместо того, чтобы делиться на каждый

элемент.

ж) diff заставляет все дифференцирования, обозначенные в expr, быть

выполненными.

и) derivlist (x, y, z...) вызывает только дифференцирования относительно

обозначенных переменных.

к) float заставляет нецелые рациональные числа быть преобразованными к

плавающей запятой.

л) numer вызывает некоторые математические функции (включая возведение в

степень) с числовыми аргументами быть вычисленными в плавающей запятой. Это

вызывает переменные в expr, которым дали numervals, который будет заменен их

значениями. Это также устанавливает float, включает.

м) pred вызывает предикаты (выражения, которые вычисляют к истинному или

ложному), чтобы быть вычисленными.

н) eval заставляет дополнительную постоценку expr происходить. (См. шаг (5)

ниже.) eval может произойти многократно, несколько раз. Для каждого случая eval,

выражение вычисляется снова.

о) A - атом, объявленный быть флагом вычисления (см. evflag), заставляет быть

обязанным к true-истинному в течение вычисления expr.

п) V: выражение (или альтернативно V=expression) заставляет V быть обязанным к

значению выражения в течение вычисления expr. Заметьте что, если V - опция Maxima,

то выражение используется для его значения в течение вычисления expr. Если больше

чем один аргумент, ev имеет этот тип тогда, закрепление делается параллельно. Если V -

неатомное выражение тогда, то замена, а не закрепление выполняется.

р) F - имя функции, как объявляли, было функцией вычисления (см. evfun),

заставляет F быть примененным к expr.

с) Любые другие имена функции (например, sum) вызывают вычисление возникших

тех имен в expr, как если бы они были глаголами-verbs.

т) Кроме того функция, встречающаяся в expr (скажем F (x)) может быть

определена локально ради этого вычисления expr, полагая F (x): = выражение как

аргумент ev.

у) Если атом, не упомянутый выше или subscripted-индексированная переменная

или subscripted-индексированное выражение дано как аргумент, это вычисляется и если

результат есть уравнение или присвоение, то выделенное закрепление или замена

выполняются. Если результат есть список, тогда члены списка рассматриваются, как

будто они были дополнительными аргументами, данными ev. Это разрешает списку

уравнений быть данными (например [X=1, Y=A ** 2]) или список имен уравнений

(например, [%t1, %t2], где %t1 и %t2 - уравнения), которые возвращают решение.

Аргументы ev могут быть даны в любом порядке, за исключением уравнений

substitution-замены, которые обработываются в последовательности, слева направо, и

функции вычисляются, которые составлены, например, ev(expr, ratsimp,

realpart), обрабатываясь как realpart (ratsimp (expr)).

Функции simp, numer, float и pred переключаются так, чтобы быть локальными в

блоке, или глобальными в Maxima так, чтобы они остались в силе до того, чтобы быть

перезагруженными.

Если expr есть canonical rational expression (CRE) — канонические рациональные

выражения, то выражение возвращается функцией ev также как CRE, если numer и

float выключатели не оба верны одновременно.

2. В течение шага (1), список делается из неиндексированных переменных,

появляющихся на левой стороне уравнений в аргументах или в значениях некоторых

аргументов, если значение - уравнение. Переменные (индексированные переменные,

которые не имеют функций ассоциированых массивов так же как неиндексированные

переменные) в выражении expr заменены их глобальными значениями, за исключением

тех, которые появляются в этом списке. Обычно, expr - только метка или % (как в %i2 в

примере ниже), таким образом этот шаг просто восстанавливает выражение, названное

меткой, так, чтобы ev мог воздействовать на это.

3. Если какие-нибудь замены обозначены аргументами, они выполняются теперь.

4. Получающееся выражение тогда перевычисляется (если один из аргументов не

был noeval), и упрощается согласно аргументам. Заметьте, что любые запросы функции

в expr будут выполнены после того, как переменные в нем вычислены и что ev(F(x))

таким образом может вести себя как F(ev (x)).

5. Для каждого случая вычисления в аргументах повторяются шаги (3) и (4).

Примеры:

(%i1) sin(x) + cos(y) + (w+1)^2 + 'diff (sin(w), w);

(%o1)

cos  ysin x' diff sinw  , w ,1w1

(%i2) ev (%, sin, expand, diff, x=2, y=1);

(%o2)

cos w w

2∗wcos11.909297426825682

Выше альтернативный уровень синтаксиса был предусмотрен для ev, посредством

чего можно только набрать его аргументы без ev(). Таким образом, можно написать

просто

expr, arg_1, ..., arg_n

Этот синтаксис не разрешен как часть другого выражения, например, в функциях,

блоках, и т.д.

Обратите внимание на параллельный обязательный процесс в следующем

примере:

(%i1) sin(x) + cos(y) + (w+1)^2 + 'diff (sin(w), w);

(%o1) cos(y)+sin(x)+'diff(sin(w),w,1)+(w+1)^2

(%i2) ev (%, sin, expand, diff, x=2, y=1);