Mavko G., Mukerji T., Dvorkin J. The Rock Physics Handbook

Подождите немного. Документ загружается.

n ¼

ðV

 2

ðV

 1

; E ¼ 2V

ð1 þ nÞ

where V

and V

are the P- and S-wave velocities, respectively. The elastic moduli

calculated from the elastic-wave velocities and density are the dynamic moduli.In

contrast, the elastic moduli calculated from deformational experiments, such as the

one shown in Figure 2.12.1, are the static moduli.

In most cases the static moduli are different from the dynamic moduli for the same

sample of rock. There are several reasons for this. One is that stress–strain relations

for rocks are often nonlinear. As a result, the ratio of stress to strain over a large-strain

measurement is different from the ratio of stress to strain over a very small-strain

measurement. Another reason is that rocks are often inelastic, affected, for example,

by frictional sliding across microcracks and grain boundaries. More internal deform-

ation can occur over a large-strain experiment than over very small-strain cycles. The

strain magnitude relevant to geomechanical processes, such as hydrofracturing, is of

the order of 10

2

, while the strain magnitude due to elastic-wave propagation is of the

order of 10

7

or less. This large strain difference affects the difference between the

static and dynamic moduli.

Relations between the dynamic and static moduli are not simple and universal

because:

(a) the elastic-wave velocity in a sample and the resulting dynamic elastic moduli

depend on the conditions of the measurement, specifically on the effective

pressure and pore fluid; and

(b) the static moduli depend on details of the loading experiment. Even for the same

type of experiment – axial loading – the static Young’s modulus may be strongly

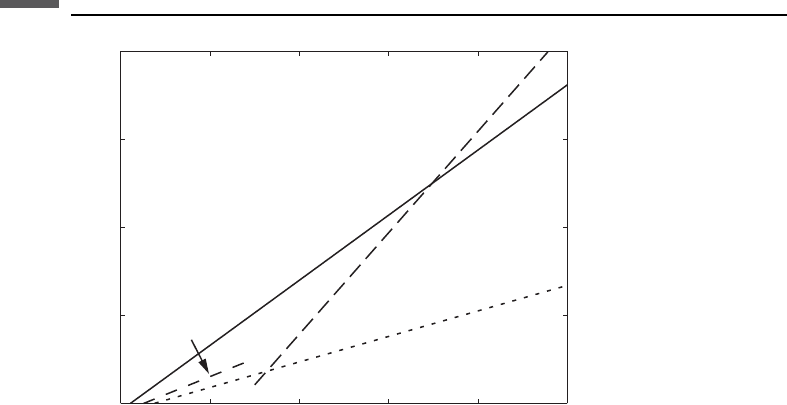
Figure 2.12.1 Uniaxial loading experiment. Dashed lines show undeformed sample,

and solid lines show deformed sample.

77 2.12 Static and dynamic moduli

affected by the overall pressure applied to the sample, as well as by the axial

deformation magnitude.

Some results have been reviewed by Scho

n(1996) and Wang and Nur ( 2000).

Presented below and in Figure 2.12.2 are some of their equations, where the moduli

are in GPa and the impedance is in km/s g/cc. In all the examples, E

stat

is the static

Young’s modulus and E

dyn

is the dynamic Young’s modulus.

Data on microcline-granite, by Belikov et al. (1970):

stat

¼ 1:137E

dyn

 9:685

Igneous and metamorphic rocks from the Canadian Shield, by King (1983):

stat

¼ 1:263E

dyn

 29:5

Granites and Jurassic sediments in the UK, by McCann and Entwisle (1992):

stat

¼ 0:69 E

dyn

þ 6:4

A wide range of rock types, by Eissa and Kazi (1988):

stat

¼ 0:74 E

dyn

 0:82

Shallow soil samples, by Gorjainov and Ljachowickij (1979) for clay:

stat

¼ 0:033E

dyn

þ 0:0065

and for sandy, wet soil:

stat

¼ 0:061E

dyn

þ 0:00285

0 10 20 30 40 50

dynamic

(GPa)

static

(GPa)

Mese and Dvorkin

Wang hard

Wang soft

Eissa and Kazi

Figure 2.12.2 Comparison of selected relations between dynamic and static Young’s moduli.

78 Elasticity and Hooke’s law

Wang and Nur (2000) for soft rocks (defined as rocks with the static Young’s

modulus < 15 GPa):

stat

¼ 0:41 E

dyn

 1:06

Wang and Nur (2000) for hard rocks (defined as rocks with the static Young’s

modulus > 15 GPa):

stat

¼ 1:153E

dyn

 15:2

Mese and Dvorkin (2000) related the static Young’s modulus and static Poisson’s

ratio (n

stat

) to the dynamic shear modulus calculated from the shear-wave velocity in

shales and shaley sands:

stat

¼ 0:59 m

dyn

 0:34; n

stat

¼0:0208m

dyn

þ 0:37

where m

dyn

is the dynamic shear modulus m

dyn

¼ V

The same data were used to obtain relations between the static moduli and the

dynamic S-wave impedance, I

S dyn

stat

¼ 1:99 I

S dyn

 3:84; n

stat

¼0:07I

S dyn

þ 0:5

as well as between the static moduli and the dynamic Young’s modulus:

stat

¼ 0:29 E

dyn

 1:1; n

stat

¼0:00743E

dyn

þ 0:34

Jizba (1991) compared the static bulk modulus, K

stat

and the dynamic bulk modulus,

dyn

, and found the following empirical relations as a function of confining pressure

in dry tight sandstones from the Travis Peak formation (Table 2.12.1).

Assumptions and limitations

There are only a handful of well-documented experimental data where large-strain

deformational experiments have been conducted with simultaneous measurement of

the dynamic P- and S-wave velocity. One of the main uncertainties in applying

Table 2.12.1 Empirical relations between static and

dynamic bulk moduli in dry tight sandstones from the

Travis Peak formation.

stat

¼ a þ bK

dyn

(GPa)

Pressure (MPa) a (GPa) b

5 0.98 0.490

20 3.16 0.567

40 1.85 0.822

125 1.85 1.13

79 2.12 Static and dynamic moduli

laboratory static moduli data in situ comes from the fact that the in-situ loading

conditions are often unknown. Moreover, in most cases, the in-situ conditions are so

complex that they are virtually impossible to reproduce in the laboratory. In most

cases, static data exhibit a strongly nonlinear stress dependence, so that it is never

clear which data point to use as the static modulus at in-situ conditions. Because of

the strongly nonlinear dependence of static moduli on the strain magnitude, the

isotropic linear elasticity equations that relate various elastic moduli to each other

might not be applicable to static moduli.

Finally, this section refers only to isotropic descriptions of static and dynamic

moduli.

80 Elasticity and Hooke’s law

Seismic wave propagation

3.1 Seismic velocities

Synopsis

The velocities of various types of seismic waves in homogeneous, isotropic, elastic

media are given by

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

K þ





ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

l þ 2



ﬃﬃﬃ





ﬃﬃﬃ



where V

is the P-wave velocity, V

is the S-wave velocity, and V

is the extensional

wave velocity in a narrow bar.

In addition, r is the density, K is the bulk modulus, m is the shear modulus, l is

Lame

’s coefficient, E is Young’s modulus, and v is Poisson’s ratio.

In terms of Poisson’s ratio one can also write

2ð1  vÞ

ð1  2vÞ

ð1 þ vÞð1  2vÞ

ð1  vÞ

¼ 2ð1 þ vÞ

v ¼

 2V

2 V

 V



 2V

The various wave velocities are related by

4  V

3  V

 4

 1

The elastic moduli can be extracted from measurements of density and any two wave

velocities. For example,

 ¼ V

K ¼  V





E ¼ V

v ¼

 2V

2 V

 V



The Rayleigh wave phase velocity V

at the surface of an isotropic homogeneous

elastic half-space is given by the solution to the equation (White, 1983)

2 



41



1=2

1 



1=2

¼ 0

(Note that the equivalent equation given in Bourbie

et al. (1987) is in error.) The

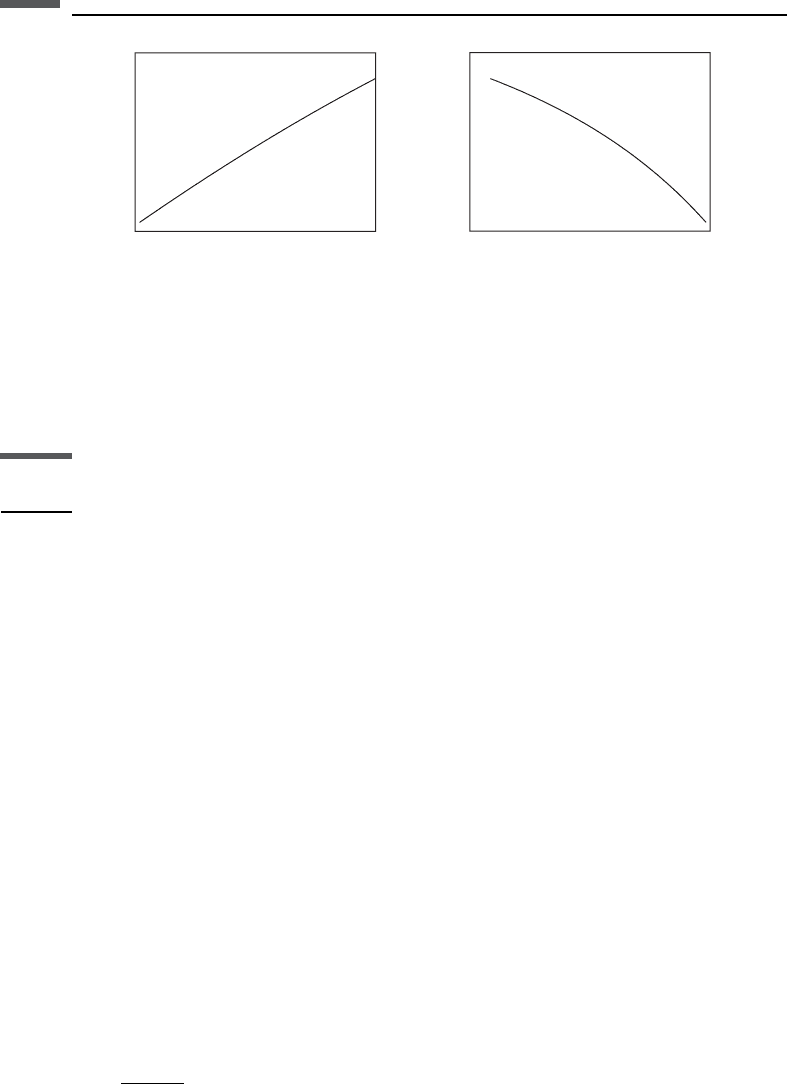
wave speed is plotted in Figure 3.1.1 and is given by

¼



1=2

1=3

þ





1=2

1=3

for



> 0

¼2

p



1=2

cos

 cos

1

ð27q

=4p

1=2

for



< 0

p ¼



16V

; q ¼

272



80V

The Rayleigh velocity at the surface of a homogeneous elastic half-space is non-

dispersive (i.e., independent of frequency).

82 Seismic wave propagation

Assumptions and limitations

These equations assume isotropic, linear, elastic media.

3.2 Phase, group, and energy velocities

Synopsis

In the physics of wave propagation we often talk about different velocities (the phase,

group, and energy velocities: V

, V

, and V

, respectively) associated with the wave

phenomenon. In laboratory measurements of core sample velocities using finite

bandwidth signals and finite-sized transducers, the velocity given by the first arrival

does not always correspond to an easily identified velocity.

A general time-harmonic wave may be defined as

Uðx; tÞ¼U

ðxÞcos½ot  pðxÞ

where o is the angular frequency and U

and p are functions of position x; U can be

any field of interest such as pressure, stress, or electromagnetic fields. The surfaces

given by p(x) ¼ constant are called cophasal or wave surfaces. In particular, for plane

waves, p(x) ¼ k·x, where k is the wave vector, or the propagation vector, and is in

the direction of propagation. For the phase to be the same at (x,t) and (x þ dx,tþ dt)

we must have

o dt ðgrad pÞdx ¼ 0

from which the phase velocity is defined as

jgrad pj

For plane waves grad p ¼ k, and hence V

¼ o/k. The reciprocal of the phase

velocity is often called the slowness, and a polar plot of slowness versus the direction

of propagation is termed the slowness surface. Phase velocity is the speed of advance

0.89

0.90

0.91

0.92

0.93

0.94

0.95

0 0.1 0.2 0.3 0.4 0.5

Poisson's ratio

0.89

0.90

0.91

0.92

0.93

0.94

0.95

0.15 0.2 0.25 0.3 0.35 0.4 0.45

)

Figure 3.1.1 Rayleigh wave phase velocity normalized by shear velocity.

83 3.2 Phase, group, and energy velocities

of the cophasal surfaces. Born and Wolf (1980) consider the phase velocity to be

devoid of any physical significance because it does not correspond to the velocity of

propagation of any signal and cannot be directly determined experimentally.

Waves encountered in rock physics are rarely perfectly monochromatic but instead

have a finite bandwidth, Do, centered around some mean frequency

o. The wave

may be regarded as a superposition of monochromatic waves of different frequencies,

which then gives rise to the concept of wave packets or wave groups. Wave packets,

or modulation on a wave containing a finite band of frequencies, propagate with the

group velocity defined as

grad @p=@oðÞ



which for plane waves becomes



The group velocity may be considered to be the velocity of propagation of the

envelope of a modulated carrier wave. The group velocity can also be expressed in

various equivalent ways as

¼V

 l

¼V

þ k



where l is the wavelength. These equations show that the group velocity is different

from the phase velocity when the phase velocity is frequency dependent, direction

dependent, or both. When the phase velocity is frequency dependent (and hence

different from the group velocity), the medium is said to be dispersive. Dispersion is

termed normal if the group velocity decreases with frequency and anomalous or

inverse if it increases with frequency (Elmore and Heald, 1985; Bourbie

et al., 1987).

In elastic, isotropic media, dispersion can arise as a result of geometric effects such as

propagation along waveguides. As a rule such geometric dispersion (Rayleigh waves,

waveguides) is normal (i.e., the group velocity decreases with frequency). In a

homogeneous viscoelastic medium, on the other hand, dispersion is anomalous or

inverse and arises owing to intrinsic dissipation.

The energy velocity V

represents the velocity at which energy propagates and

may be defined as

84 Seismic wave propagation

where P

is the average power flow density and E

is the average total energy

density.

In isotropic, homogeneous, elastic media all three velocities are the same. In a lossless

homogeneous medium (of arbitrary symmetry), V

and V

are identical, and energy

propagates with the group velocity. In this case the energy velocity may be obtained

from the group velocity, which is usually somewhat easier to compute. If the medium is

not strongly dispersive and a wave group can travel a measurable distance without

appreciable “smearing” out, the group velocity may be considered to represent the

velocity at which the energy is propagated (though this is not strictly true in general).

In anisotropic, homogeneous, elastic media, the phase velocity, in general, differs

from the group velocity (which is equal to the energy velocity because the medium is

elastic) except along certain symmetry directions, where they coincide. The direction

in which V

is deflected away from k (which is also the direction of V

) is obtained

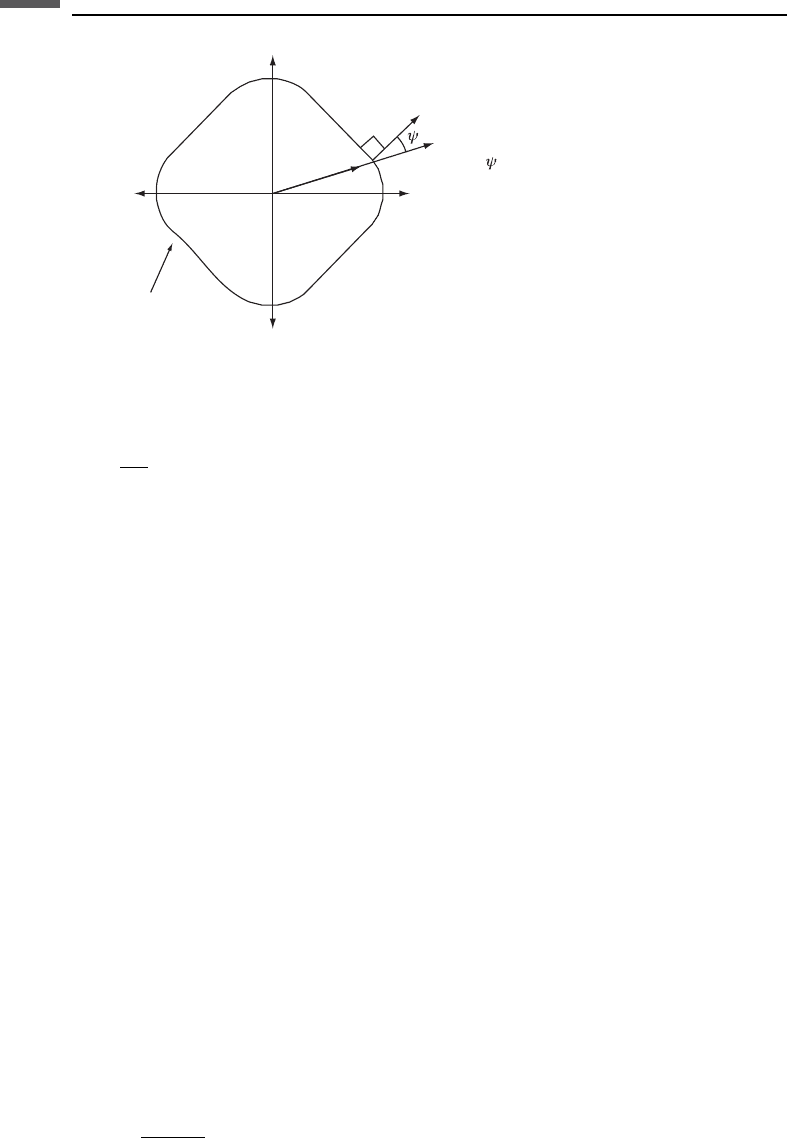
from the slowness surface (shown in Figure 3.2.1), for V

(¼ V

in elastic media) must

always be normal to the slowness surface (Auld, 1990).

The group velocity in anisotropic media maybecalculatedbydifferentiationof

the dispersion relation obtained in an implicit form from the Christoffel equation given by

ijkl

 o



j¼ðo; k

; k

Þ¼0

where c

ijkl

is the stiffness tensor, n

are the direction cosines of k, r is the density, and

is the Kronecker delta function. The group velocity is then evaluated as

¼



@=@o

where the gradient is with respect to k

, k

, and k

= V

cos

anisotropic slowness

surface

Figure 3.2.1 In anisotropic media, energy propagates along V

, which is always normal to the

slowness surface and in general is deflected by the angle c away from V

and the wave vector k.

85 3.2 Phase, group, and energy velocities

The concept of group velocity is not strictly applicable to attenuating viscoelastic

media, but the energy velocity is still well defined (White, 1983). The energy

propagation velocity in a dissipative medium is neither the group velocity nor the

phase velocity except when

(1) the medium is infinite, homogeneous, linear, and viscoelastic, and

(2) the wave is monochromatic and homogeneous, i.e., planes of equal phase are

parallel to planes of equal amplitude, or, in other words, the real and imaginary

parts of the complex wave vector point in the same direction (in general they do

not), in which case the energy velocity is equal to the phase velocity (Ben-

Menahem and Singh, 1981; Bourbie

et al., 1987).

For the special case of a Voigt solid (see Section 3.8 on viscoelasticity) the energy

transport velocity is equal to the phase velocity at all frequencies. For wave propaga-

tion in dispersive, viscoelastic media, one sometimes defines the limit

¼ lim

o!1

ðoÞ

which describes the propagation of a well-defined wavefront and is referred to as the

signal velocity (Beltzer, 1988).

Sometimes it is not clear which velocities are represented by the recorded travel

times in laboratory ultrasonic core sample measurements, especially when the sample

is anisotropic. For elastic materials, there is no ambiguity for propagation along

symmetry directions because the phase and group velocities are identical. For non-

symmetry directions, the energy does not necessarily propagate straight up the axis of

the core from the transducer to the receiver. Numerical modeling of laboratory

experiments (Dellinger and Vernik, 1992) indicates that, for typical transducer widths

(10 mm), the recorded travel times correspond closely to the phase velocity. Accurate

measurement of group velocity along nonsymmetry directions would essentially

require point transducers of less than 2 mm width.

According to Bourbie

et al. (1987), the velocity measured by a resonant-bar

standing-wave technique corresponds to the phase velocity.

Assumptions and limitations

In general, phase, group, and energy velocities may differ from each other in both

magnitude and direction. Under certain conditions two or more of them may become

identical. For homogeneous, linear, isotropic, elastic media all three are the same.

3.3 NMO in isotropic and anisotropic media

Synopsis

The two-way seismic travel time, t, of a pure (nonconverted) mode from the surface,

through a homogeneous, isotropic, elastic layer, to a horizontal reflector is hyperbolic

86 Seismic wave propagation