Mavko G., Mukerji T., Dvorkin J. The Rock Physics Handbook

Подождите немного. Документ загружается.

Assumptions and limitations



The existence of effective-pressure laws assumes that the rocks are hyperelastic, i.e.,

there is no hysteresis or rate dependence in the relation between stress and strain.



Rocks are extremely variable, so effective-pressure behavior can likewise be variable.

2.7 Stress-induced anisotropy in rocks

Synopsis

The closing of cracks under compressive stress (or, equivalently, the stiffening of

compliant grain contacts) tends to increase the effective elastic moduli of rocks (see

also Section 2.5 on third-order elasticity).

When the crack population is anisotropic, either in the original unstressed condi-

tion or as a result of the stress field, then this condition can impact the overall elastic

anisotropy of the rock. Laboratory demonstrations of stress-induced anisotropy have

been reported by numerous authors (Nur and Simmons, 1969a; Lockner et al., 1977;

Zamora and Poirier, 1990; Sayers et al., 1990; Yin, 1992; Cruts et al., 1995).

The simplest case to understand is a rock with a random (isotropic) distribution of

cracks embedded in an isotropic mineral matrix. In the initial unstressed state, the

rock is elastically isotropic. If a hydrostatic compressive stress is applied, cracks in

all directions respond similarly, and the rock remains isotropic but becomes stiffer.

However, if a uniaxial compressive stress is applied, cracks with normals parallel or

nearly parallel to the applied-stress axis will tend to close preferentially, and the rock

will take on an axial or transversely isotropic symmetry.

An initially isotropic rock with arbitrary stress applied will have at least ortho-

rhombic symmetry (Nur, 1971; Rasolofosaon, 1998), provided that the stress-induced

changes in moduli are small relative to the absolute moduli.

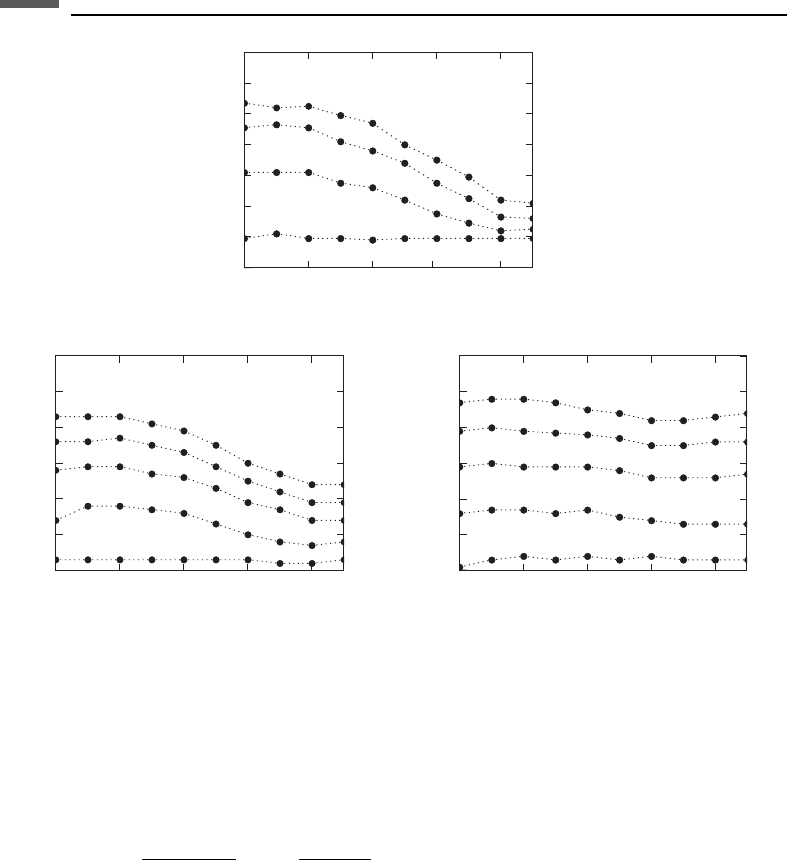
Figure 2.7.1 illustrates the effects of stress-induced crack alignment on seismic-

velocity anisotropy discovered in the laboratory by Nur and Simmons (1969a). The

crack porosity of the dry granite sample is essentially isotropic at low stress.

As uniaxial stress is applied, crack anisotropy is induced. The velocities (compres-

sional and two polarizations of shear) clearly vary with direction relative to the stress-

induced crack alignment. Table 2.7.1 summarizes the elastic symmetries that result

when various applied-stress fields interact with various initial crack symmetries

(Paterson and Weiss, 1961; Nur, 1971).

A rule of thumb is that a wave is most sensitive to cracks when its direction of

propagation or direction of polarization is perpendicular (or nearly so) to the crack faces.

The most common approach to modeling the stress-induced anisotropy is to assume

angular distributions of idealized penny-shaped cracks (Nur, 1971; Sayers, 1988a, b;

Gibson and Tokso

z, 1990). The stress dependence is introduced by assuming or

inferring distributions or spectra of crack aspect ratios with various orientations.

47 2.7 Stress-induced anisotropy in rocks

The assumption is that a crack will close when the component of applied compres-

sive stress normal to the crack faces causes a normal displacement of the crack faces

equal to the original half-width of the crack. This allows us to estimate the crack

closing stress as follows:



3pð1  2nÞ

4ð1  n

2ð1  nÞ

where a is the aspect ratio of the crack, and n, m

, and K

are the Poisson ratio, shear

modulus, and bulk modulus of the mineral, respectively (see Section 2.9 on the

deformation of inclusions and cavities in elastic solids). Hence, the thinnest cracks

will close first, followed by thicker ones. This allows one to estimate, for a given

aspect-ratio distribution, how many cracks remain open in each direction for any

applied stress field. These inferred crack distributions and their orientations can be

put into one of the popular crack models (e.g., Hudson, 1981) to estimate the resulting

effective elastic moduli of the rock. Although these penny-shaped crack models have

been relatively successful and provide a useful physical interpretation, they are

limited to low crack concentrations and may not effectively represent a broad range

of crack geometries (see Section 4.10 on Hudson’s model for cracked media).

3.6

3.8

4.0

4.2

4.4

4.6

4.8

5.0

020406080

Angle from stress axis (deg)

Stress (bars)

100

200

300

(km/s)

2.6

2.7

2.8

2.9

3.0

3.1

3.2

0 20406080

le from stress axis (de

)

Stress (bars)

100

200

300

400

2.6

2.7

2.8

2.9

3.0

3.1

3.2

20 40 60 80

le from stress axis (de

)

Stress (bars)

100

200

300

400

(SV) (km/s)

(SH) (km/s)

Figure 2.7.1 The effects of stress-induced crack alignment on seismic-velocity anisotropy measured

in the laboratory (Nur and Simmons, 1969a).

48 Elasticity and Hooke’s law

As an alternative, Mavko et al. ( 1995) presented a simple recipe for estimating

stress-induced velocity anisotropy directly from measured values of isotropic V

and

versus hydrostatic pressure. This method differs from the inclusion models,

because it is relatively independent of any assumed crack geometry and is not limited

to small crack densities. To invert for a particular crack distribution, one needs to

assume crack shapes and aspect-ratio spectra. However, if rather than inverting for a

crack distribution, we instead directly transform hydrostatic velocity–pressure data to

stress-induced velocity anisotropy, we can avoid the need for parameterization in

terms of ellipsoidal cracks and the resulting limitations to low crack densities. In this

sense, the method of Mavko et al. (1995) provides not only a simpler but also a more

general solution to this problem, for ellipsoidal cracks are just one particular case of

the general formulation.

Table 2.7.1 Dependence of symmetry of induced velocity anisotropy on initial crack

distribution and applied stress and its orientation.

Symmetry of initial

crack distribution Applied stress

Orientation of

applied stress

Symmetry of induced

velocity anisotropy

Number of

elastic

constants

Random Hydrostatic Isotropic 2

Uniaxial Axial 5

Triaxial

Orthorhombic 9

Axial Hydrostatic Axial 5

Uniaxial Parallel to axis

of symmetry

Axial 5

Uniaxial Normal to axis

of symmetry

Orthorhombic 9

Uniaxial Inclined Monoclinic 13

Triaxial

Parallel to axis

of symmetry

Orthorhombic 9

Triaxial

Inclined Monoclinic 13

Orthorhombic Hydrostatic Orthorhombic 9

Uniaxial Parallel to axis

of symmetry

Orthorhombic 9

Uniaxial Inclined in plane

of symmetry

Monoclinic 13

Uniaxial Inclined Triclinic 21

Triaxial

Parallel to axis

of symmetry

Orthorhombic 9

Triaxial

Inclined in plane

of symmetry

Monoclinic 13

Triaxial

Inclined Triclinic 21

Note:

Three generally unequal principal stresses.

49 2.7 Stress-induced anisotropy in rocks

The procedure is to estimate the generalized pore-space compliance from the

measurements of isotropic V

and V

. The physical assumption that the compliant

part of the pore space is crack-like means that the pressure dependence of the

generalized compliances is governed primarily by normal tractions resolved across

cracks and defects. These defects can include grain boundaries and contact regions

between clay platelets (Sayers, 1995). This assumption allows the measured

pressure dependence to be mapped from the hydrostatic stress state to any applied

nonhydrostatic stress.

The method applies to rocks that are approximately isotropic under hydrostatic

stress and in which the anisotropy is caused by crack closure under stress. Sayers

(1988b) also found evidence for some stress-induced opening of cracks, which is

ignored in this method. The potentially important problem of stress–strain hysteresis

is also ignored.

The anisotropic elastic compliance tensor S

ijkl

(s) at any given stress state s may be

expressed as

S

ijkl

ðÞ¼S

ijkl

ðÞS

ijkl

p=2

y¼0

¼0

3333



mÞ4W

2323



mÞ



sin y dy d

p=2

y¼0

¼0

2323



mÞ d

þ d



þd



sin y dy d

where

3333

ðpÞ¼

S

iso

jjkk

ðpÞ

2323

ðpÞ¼

½S

iso

abab

ðpÞS

iso

aabb

ðpÞ

The tensor S

ijkl

denotes the reference compliance at some very large confining

hydrostatic pressure when all of the compliant parts of the pore space are closed. The

expression  S

iso

ijkl

ðpÞ¼S

iso

ijkl

ðpÞS

ijkl

describes the difference between the compli-

ance under a hydrostatic effective pressure p and the reference compliance at high

pressure. These are determined from measured P- and S-wave velocities versus the

hydrostatic pressure. The tensor elements W

3333

and W

2323

are the measured normal

and shear crack compliances and include all interactions with neighboring cracks and

pores. These could be approximated, for example, by the compliances of idealized

ellipsoidal cracks, interacting or not, but this would immediately reduce the general-

ity. The expression

m ðsin y cos ; sin y sin ; cos yÞ

denotes the unit normal to the

crack face, where y and f are the polar and azimuthal angles in a spherical coordinate

system, respectively.

50 Elasticity and Hooke’s law

An important physical assumption in the preceding equations is that, for thin

cracks, the crack compliance tensor W

ijkl

is sparse, and thus only W

3333

, W

1313

, and

2323

are nonzero. This is a general property of planar crack formulations and reflects

an approximate decoupling of normal and shear deformation of the crack and

decoupling of the in-plane and out-of-plane deformations. This allows us to write

jjkk

 W

3333

. Furthermore, it is assumed that the two unknown shear compliances

are approximately equal: W

1313

 W

2323

. A second important physical assumption is

that for a thin crack under any stress field, it is primarily the normal component of

stress,  ¼



m, resolved on the faces of a crack, that causes it to close and to have

a stress-dependent compliance. Any open crack will have both normal and shear

deformation under normal and shear loading, but it is only the normal stress that

determines crack closure.

For the case of uniaxial stress s

applied along the 3-axis to an initially isotropic

rock, the normal stress in any direction is s

¼ s

cos

y. The rock takes on a

transversely isotropic symmetry, with five independent elastic constants. The five

independent components of DS

ijkl

become

S

uni

3333

¼ 2p

p=2

½W

3333

ð

cos

yÞ4W

2323

ð

cos

yÞcos

y sin y dy

þ 2p

p=2

2323

ð

cos

yÞcos

y sin y dy

S

uni

1111

¼ 2p

p=2

½W

3333

ð

cos

yÞ4W

2323

ð

cos

yÞsin

y sin y dy

þ 2p

p=2

2323

ð

cos

yÞsin

y sin y dy

S

uni

1122

¼ 2p

p=2

½W

3333

ð

cos

yÞ4W

2323

ð

cos

yÞsin

y sin y dy

S

uni

1133

¼ 2p

p=2

½W

3333

ð

cos

yÞ4W

2323

ð

cos

yÞsin

y cos

y sin y dy

S

uni

2323

¼ 2p

p=2

½W

3333

ð

cos

yÞ4W

2323

ð

cos

yÞsin

y cos

y sin y dy

þ 2p

p=2

2323

ð

cos

yÞsin

y sin y dy

þ 2p

p=2

2323

ð

cos

yÞcos

y sin y dy

Note that in the above equations, the terms in parentheses with W

2323

ðÞ and

3333

ðÞ are arguments to the W

2323

and W

3333

pressure functions, and not multiplica-

tive factors.

Sayers and Kachanov (1991, 1995) have presented an equivalent formalism for

stress-induced anisotropy. The elastic compliance S

ijkl

is once again written in the form

51 2.7 Stress-induced anisotropy in rocks

S

ijkl

¼ S

ijkl

ðÞS

ijkl

where S

ijkl

is the compliance in the absence of compliant cracks and grain boundaries

and DS

ijkl

is the excess compliance due to the cracks. DS

ijkl

can be written as

S

ijkl

ðd

þ d

Þþb

ijkl

where a

is a second-rank tensor and b

ijkl

is a fourth-rank tensor defined by

ðrÞ

ðr Þ

ijkl

ðr Þ

 B

ðrÞ



ðr Þ

ðrÞ

In these expressions, the summation is over all grain contacts and microcracks within

the rock volume V. B

ðr Þ

and B

ðrÞ

are the normal and shear compliances of the rth

discontinuity, which relate the displacement discontinuity across the crack to the

applied traction across the crack faces; n

ðrÞ

, is the ith component of the normal to the

discontinuity, and A

(r)

is the area of the discontinuity.

A completely different strategy for quantifying stress-induced anisotropy is to use

the formalism of third-order elasticity, described in Section 2.5 (e.g., Helbig, 1994;

Johnson and Rasolofosaon, 1996; Prioul et al., 2004). The third-order elasticity

approach is phenomenological, avoiding the physical mechanisms of stress sensitiv-

ity, but providing a compact notation. For example, Prioul et al. (2004) found that for

a stressed VTI (transversely isotropic with vertical symmetry axis) material, the

effective elastic constants can be approximated in Voigt notation as

eff

 c

þ c

111

þ c

112

ðe

þ e

eff

 c

þ c

111

þ c

112

ðe

þ e

eff

 c

þ c

111

þ c

112

ðe

þ e

eff

 c

þ c

112

ðe

þ e

Þþc

123

eff

 c

þ c

112

ðe

þ e

Þþc

123

eff

 c

þ c

112

ðe

þ e

Þþc

123

eff

 c

þ c

144

þ c

155

ðe

þ e

eff

 c

þ c

144

þ c

155

ðe

þ e

eff

 c

þ c

144

þ c

155

ðe

þ e

where the constants c

, c

are the VTI elastic constants at the

unstressed reference state, with c

¼ c

 2c

. The quantities e

, e

, and e

are

the principal strains, computed from the applied stress using the conventional

Hooke’s law, e

¼ s

ijkl



. For these expressions, it is assumed that the direction of

52 Elasticity and Hooke’s law

the applied principal stress is aligned with the VTI symmetry (x

-) axis. Furthermore,

for these expressions it is assumed that the stress-sensitive third-order tensor is

isotropic, defined by the three independent constants, c

111

, c

112

, and c

123

with

144

¼ðc

112

 c

123

Þ=2 and c

155

¼ðc

111

 c

112

Þ=4.

In practice, the elastic constants (five for the unstressed VTI rock and three for the

third-order elasticity) can be estimated from laboratory measurements, as illustrated

by Sarkar et al. (2003) and Prioul et al. (2004). For an intrinsically VTI rock,

hydrostatic loading experiments provide sufficient information to invert for all three

of the third-order constants, provided that the anisotropy is not too weak. However,

for an intrinsically isotropic rock, nonhydrostatic loading is required in order to

provide enough independent information to determine the constants. Once the con-

stants are determined, the stress-induced elastic constants corresponding to any

(aligned) stress field can be determined. The full expressions for stress-induced

anisotropy of an originally VTI rock are given by Sarkar et al. (2003) and Prioul

et al. (2004).

Sarkar et al. (2003) give expressions for stress-induced changes in Thomsen

parameters of an originally VTI rock, provided that both the original and stress-

induced anisotropies are weak:

ð1Þ

¼ e

155

ð

 

Þ; e

ð2Þ

¼ e

155

ð

 

ð1Þ

¼ d

155

ð

 

Þ; d

ð2Þ

¼ d

155

ð

 

ð1Þ

¼ g

456

ð

 

Þ; g

ð2Þ

¼ g

456

ð

 

ð3Þ

155

ð

 

155

ðc

111

 c

112

Þ; c

456

ðc

111

 3c

112

þ 2c

123

The results are shown in terms of Tsvankin’s extended Thomsen parameters

(Section 2.4). Orthorhombic symmetry occurs when 

6¼ 

. (Strictly speaking,

three different principal stresses applied to a VTI rock do not result in perfect

orthorhombic symmetry. However, orthorhombic parameters are adequate in the case

of weak anisotropy.)

Uses

Understanding or, at least, empirically describing the stress dependence of velocities

is useful for quantifying the change of velocities in seismic time-lapse data due to

changes in reservoir pressure, as well as in certain types of naturally occurring

overpressure. Since the state of stress in situ is seldom hydrostatic, quantifying the

impact of stress on anisotropy can often improve on the usual isotropic analysis.

53 2.7 Stress-induced anisotropy in rocks

Assumptions and limitations



Most models for predicting or describing stress-induced anisotropy that are based on

cracks and crack-like flaws assume an isotropic, linear, elastic solid mineral material.



Methods based on ellipsoidal cracks or spherical contacts are limited to idealized

geometries and to low crack densities.



The method of Mavko et al. (1995) has been shown to sometimes under predict

stress-induced anisotropy when the maximum stress difference is comparable to

the mean stress magnitude. More generally, there is evidence (Johnson and

Rasolofosaon, 1996) that classical elastic formulations (nonlinear elasticity) can

fail to describe the behavior of rocks at low stresses.



The methods presented here assume that the strains are infinitesimal. When strains

become finite, an additional source of nonlinearity, called geometrical or kinetic non-

linearity, appears, related to the difference between Lagrangian and Eulerian descrip-

tions of motion (Zarembo and Krasil’nikov, 1971; Johnson and Rasolofosaon, 1996).

2.8 Strain components and equations of motion in cylindrical

and spherical coordinate systems

Synopsis

The equations of motion and the expressions for small-strain components in cylin-

drical and spherical coordinate systems differ from those in a rectangular coordinate

system. Figure 2.8.1 shows the variables used in the equations that follow.

In the cylindrical coordinate system (r, f, z), the coordinates are related to those in

the rectangular coordinate system (x, y, z)as

r ¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

þ y

; tanðÞ¼

x ¼ r cosðÞ; y ¼ r sinðÞ; z ¼ z

The small-strain components can be expressed through the displacements u

, and

(which are in the directions r, f, and z, respectively) as

; e





@

; e

r

@









z



@



; e



The equations of motion are

@

r

@

@



 



¼ 

54 Elasticity and Hooke’s law

@

r

@



@

@

z

2

r

¼ 



@

z

@

@



¼ 

where r denotes density and t time.

In the spherical coordinate system (r, f, y) the coordinates are related to those in

the rectangular coordinate system (x, y, z)as

r ¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

þ y

þ z

; tanðÞ¼

; cosðyÞ¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

þ y

þ z

x ¼ r sinðyÞcosðÞ; y ¼ r sinðyÞsinðÞ; z ¼ r cosðyÞ

The small-strain components can be expressed through the displacements u

, and

(which are in the directions r, f, and y, respectively) as

; e



r sinðyÞ



@

r tanðyÞ

; e

r

r sinðyÞ

@









y



@





r tanðyÞ

r sinðyÞ

@







The equations of motion are

@

r sinðyÞ

@

r

@

@

2

þ 

cotðyÞ



 

¼ 

@

r

r sinðyÞ

@



@

@

y

3

r

þ 

y

cotðyÞ

¼ 



@

r sinðyÞ

@



@

@

y

3

þð

 



ÞcotðyÞ

¼ 

Cylindrical

coordinates

Spherical

coordinates

Figure 2.8.1 The variables used for converting between Cartesian, spherical,

and cylindrical coordinates.

55 2.8 Strain components and equations of motion

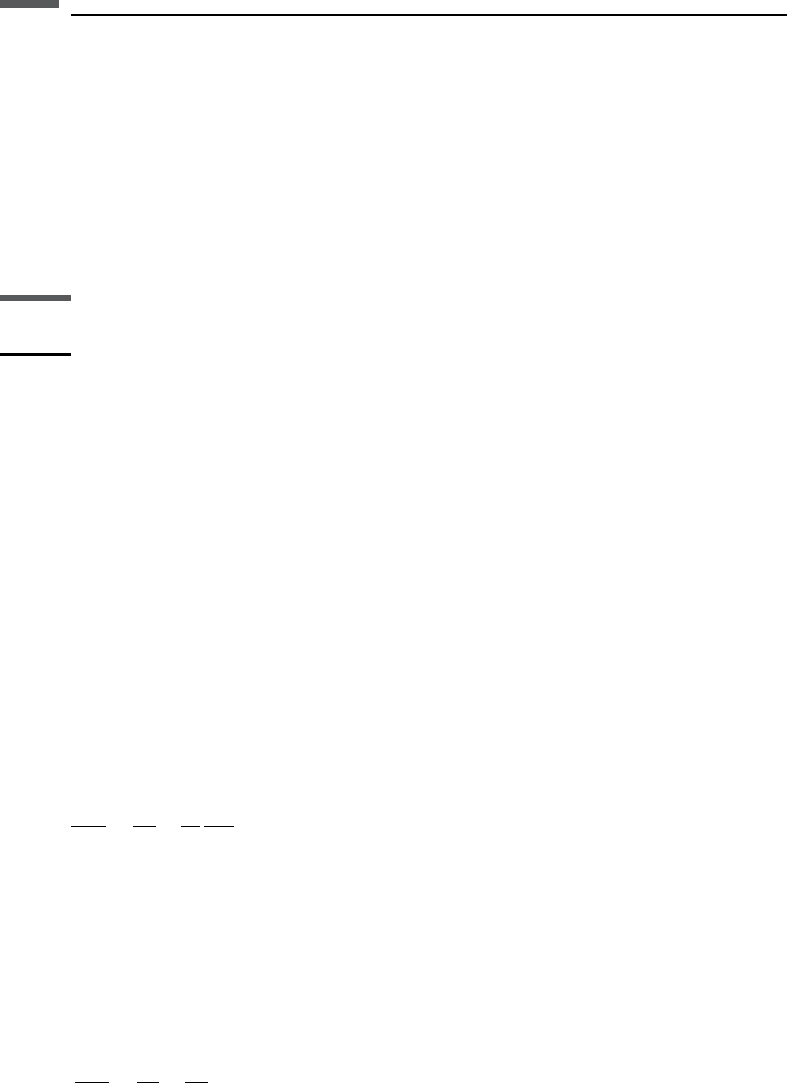
Uses

The foregoing equations are used to solve elasticity problems where cylindrical or

spherical geometries are most natural.

Assumptions and limitations

The equations presented assume that the strains are small.

2.9 Deformation of inclusions and cavities in elastic solids

Synopsis

Many problems in effective-medium theory and poroelasticity can be solved or

estimated in terms of the elastic behavior of cavities and inclusions. Some static

and quasistatic results for cavities are presented here. It should be remembered that

often these are also valid for certain limiting cases of dynamic problems. Excellent

treatments of cavity deformation and pore compressibility are given by Jaeger and

Cook (1969) and by Zimmerman (1991a).

General pore deformation

Effective dry compressibility

Consider a homogeneous linear elastic solid that has an arbitrarily shaped pore space –

either a single cavity or a collection of pores. The effective dry compressibility (i.e.,

the reciprocal of the dry bulk modulus) of the porous solid can be written as

dry





@

@



dry

where K

dry

is the effective bulk modulus of the dry porous solid, K

is the bulk

modulus of the solid mineral material,  is the porosity, 

is the pore volume,

@

=@j

dry

is the derivative of the pore volume with respect to the externally applied

hydrostatic stress. We also assume that no inelastic effects such as friction or

viscosity are present. This is strictly true, regardless of the pore geometry and the

pore concentration. The preceding equation can be rewritten slightly as

dry



where K



¼ 

=ð@

=@Þj

dry

is defined as the dry pore-space stiffness. These equa-

tions state simply that the porous rock compressibility is equal to the intrinsic mineral

compressibility plus an additional compressibility caused by the pore space.

56 Elasticity and Hooke’s law