Mavko G., Mukerji T., Dvorkin J. The Rock Physics Handbook

Подождите немного. Документ загружается.

missing. Drawing with replacement from the data is equivalent to Monte Carlo

realizations from the empirical CDF. The statistic of interest is computed on all of

the replicate bootstrap data sets. The distribution of the bootstrap replicates of the

statistic is a measure of uncertainty of the statistic.

Drawing bootstrap replicates from the empirical CDF in this way is sometimes

termed nonparametric bootstrap.Inparametric bootstrap the data are first mod-

eled by a parametric CDF (e.g., a multivariate Gaussian), and then bootstrap data

replicates are drawn from the modeled CDF. Both simple bootstrap techniques

described above assume the data are independent and identically distributed. More

sophisticated bootstrap techniques exist that can account for data dependence.

Statistical classification

The goal in statistical classification problems is to predict the class of an unknown

sample based on observed attributes or features of the sample. For example, the

observed attributes could be P and S impedances, and the classes could be lithofacies,

such as sand and shale. The classes are sometimes also called states, outcomes, or

responses, while the observed features are called the predictors. Discussions concerning

many modern classification methods may be found in Fukunaga (1990), Duda et al.

(2000), Hastie et al. (2001), and Bishop (2006).

There are two general types of statistical classification: supervised classification,

which uses a training data set of samples for which both the attributes and classes

have been observed; and unsupervised learning, for which only the observed

attributes are included in the data. Supervised classification uses the training data

to devise a classification rule, which is then used to predict the classes for new data,

where the attributes are observed but the outcomes are unknown. Unsupervised

learning tries to cluster the data into groups that are statistically different from each

other based on the observed attributes.

A fundamental approach to the supervised classification problem is provided by

Bayesian decision theory. Let x denote the univariate or multivariate input attributes,

and let c

, j ¼1,..., N denote the N different states or classes. The Bayes formula

expresses the probability of a particular class given an observed x as

Pðc

jxÞ¼

Pðx; c

PðxÞ

Pðx jc

ÞPðc

PðxÞ

where P(x, c

) denotes the joint probability of x and c

; P(x jc

) denotes the conditional

probability of x given c

; and P(c

) is the prior probability of a particular class. Finally,

P(x) is the marginal or unconditional pdf of the attribute values across all N states.

It can be written as

PðXÞ¼

j¼1

PðX jc

ÞPðc

17 1.3 Statistics and probability

and serves as a normalization constant. The class-conditional pdf, P(x jc

), is estimated

from the training data or from a combination of training data and forward models.

The Bayes classification rule says:

classify as class c

if Pðc

jxÞ > Pðc

jxÞ for all j 6¼ k:

This is equivalent to choosing c

when P(x jc

)P(c

) > P(x jc

)P(c

) for all j 6¼ k.

The Bayes classification rule is the optimal one that minimizes the misclassifica-

tion error and maximizes the posterior probability. Bayes classification requires

estimating the complete set of class-conditional pdfs P(x jc

). With a large number

of attributes, getting a good estimate of the highly multivariate pdf becomes difficult.

Classification based on traditional discriminant analysis uses only the means and

covariances of the training data, which are easier to estimate than the complete pdfs.

When the input features follow a multivariate Gaussian distribution, discriminant

classification is equivalent to Bayes classification, but with other data distribution

patterns, the discriminant classification is not guaranteed to maximize the posterior

probability. Discriminant analysis classifies new samples according to the minimum

Mahalanobis distance to each class cluster in the training data. The Mahalanobis

distance is defined as follows:

¼ x  m





1

x  m



where x is the sample feature vector (measured attribute), m

are the vectors of the

attribute means for the different categories or classes, and S is the training data

covariance matrix. The Mahalanobis distance can be interpreted as the usual Euclidean

distance scaled by the covariance, which decorrelates and normalizes the components

of the feature vector. When the covariance matrices for all the classes are taken to be

identical, the classification gives rise to linear discriminant surfaces in the feature

space. More generally, with different covariance matrices for each category, the

discriminant surfaces are quadratic. If the classes have unequal prior probabilities, the

term ln[P(class)

] is added to the right-hand side of the equation for the Mahalanobis

distance, where P(class)

is the prior probability for the jth class. Linear and quadratic

discriminant classifiers are simple, robust classifiers and often produce good results,

performing among the top few classifier algorithms.

1.4 Coordinate transformations

Synopsis

It is often necessary to transform vector and tensor quantities in one coordinate

system to another more suited to a particular problem. Consider two right-hand

rectangular Cartesian coordinates (x, y, z) and (x

) with the same origin, but

18 Basic tools

with their axes rotated arbitrarily with respect to each other. The relative orientation

of the two sets of axes is given by the direction cosines b

, where each element is

defined as the cosine of the angle between the new i

-axis and the original j-axis. The

variables b

constitute the elements of a 3 3 rotation matrix [b]. Thus, b

is the

cosine of the angle between the 2-axis of the primed coordinate system and the 3-axis

of the unprimed coordinate system.

The general transformation law for tensors is

ABCD...

¼ b

...M

abcd...

where summation over repeated indices is implied. The left-hand subscripts (A, B,

C, D,...)on thebs match the subscripts of the transformed tensor M

on the left, and

the right-hand subscripts (a, b, c, d,...)match the subscripts of M on the right. Thus

vectors, which are first-rank tensors, transform as

¼ b

or, in matrix notation, as

whereas second-rank tensors, such as stresses and strains, obey



¼ b



½

¼½b½½b

in matrix notation. Elastic stiffnesses and compliances are, in general, fourth-order

tensors and hence transform according to

ijkl

¼ b

pqrs

Often c

ijkl

and s

ijkl

are expressed as the 6 6 matrices C

and S

, using the

abbreviated 2-index notation, as defined in Section 2.2 on anisotropic elasticity. In this

case, the usual tensor transformation law is no longer valid, and the change of coordin-

ates is more efficiently performed with the 6 6 Bond transformation matrices

M and N, as explained below (Auld, 1990):

½C

¼½M½C½M

½S

¼½N½S½N

19 1.4 Coordinate transformations

The elements of the 6 6 M and N matrices are given in terms of the direction

cosines as follows:

M ¼

þ b

and

N ¼

þ b

The advantage of the Bond method for transforming stiffnesses and compliances is

that it can be applied directly to the elastic constants given in 2-index notation, as

they almost always are in handbooks and tables.

Assumptions and limitations

Coordinate transformations presuppose right-handed rectangular coordinate systems.

20 Basic tools

Elasticity and Hooke’s law

2.1 Elastic moduli: isotropic form of Hooke’s law

Synopsis

In an isotropic, linear elastic material, the stress and strain are related by Hooke’s law

as follows (e.g., Timoshenko and Goodier, 1934):



¼ ld

þ 2me

½ð1 þ nÞ

 nd





where

¼ elements of the strain tensor



¼ elements of the stress tensor

¼ volumetric strain (sum over repeated index)



¼ mean stress times 3 (sum over repeated index)

¼ 0ifi 6¼ j and d

¼ 1ifi ¼ j

In an isotropic, linear elastic medium, only two constants are needed to specify the

stress–strain relation completely (for example, [l, m] in the first equation or [E, v],

which can be derived from [l, m], in the second equation). Other useful and conveni-

ent moduli can be defined, but they are always relatable to just two constants. The

three moduli that follow are examples.

The Bulk modulus, K, is defined as the ratio of the hydrostatic stress, s

, to the

volumetric strain:



¼ Ke

The bulk modulus is the reciprocal of the compressibility, b, which is widely used to

describe the volumetric compliance of a liquid, solid, or gas:

b ¼

Caution

Occasionally in the literature authors have used the term incompressibility as an

alternate name for Lame

’s constant, l, even though l is not the reciprocal of the

compressibility.

The shear modulus, m, is defined as the ratio of the shear stress to the shear strain:



¼ 2me

; i 6¼ j

Young’s modulus, E, is defined as the ratio of the extensional stress to the exten-

sional strain in a uniaxial stress state:



¼ Ee

;

¼ 

¼ 0

Poisson’s ratio, which is defined as minus the ratio of the lateral strain to the axial

strain in a uniaxial stress state:

v ¼

;

¼ 

¼ 0

P-wave modulus, M ¼ V

, defined as the ratio of the axial stress to the axial strain

in a uniaxial strain state:



¼ Me

; e

¼ e

¼ 0

Note that the moduli (l, m, K, E, M) all have the same units as stress (force/area),

whereas Poisson’s ratio is dimensionless.

Energy considerations require that the following relations always hold. If they do

not, one should suspect experimental errors or that the material is not isotropic:

K ¼ l þ

 0; m  0

1 < n 

; E  0

In rocks, we seldom, if ever, observe a Poisson’s ratio of less than 0. Although

permitted by this equation, a negative measured value is usually treated with suspi-

cion. A Poisson’s ratio of 0.5 can mean an infinitely incompressible rock (not

possible) or a liquid. A suspension of particles in fluid, or extremely soft, water-

saturated sediments under essentially zero effective stress, such as pelagic ooze, can

have a Poisson’s ratio approaching 0.5.

Although any one of the isotropic constants (l, m, K, M, E, and n) can be derived in

terms of the others, m and K have a special significance as eigenelastic constants

(Mehrabadi and Cowin, 1989)orprincipal elasticities of the material (Kelvin, 1856).

The stress and strain eigentensors associated with m and K are orthogonal, as discussed

in Section 2.2. Such an orthogonal significance does not hold for the pair l and m.

22 Elasticity and Hooke’s law

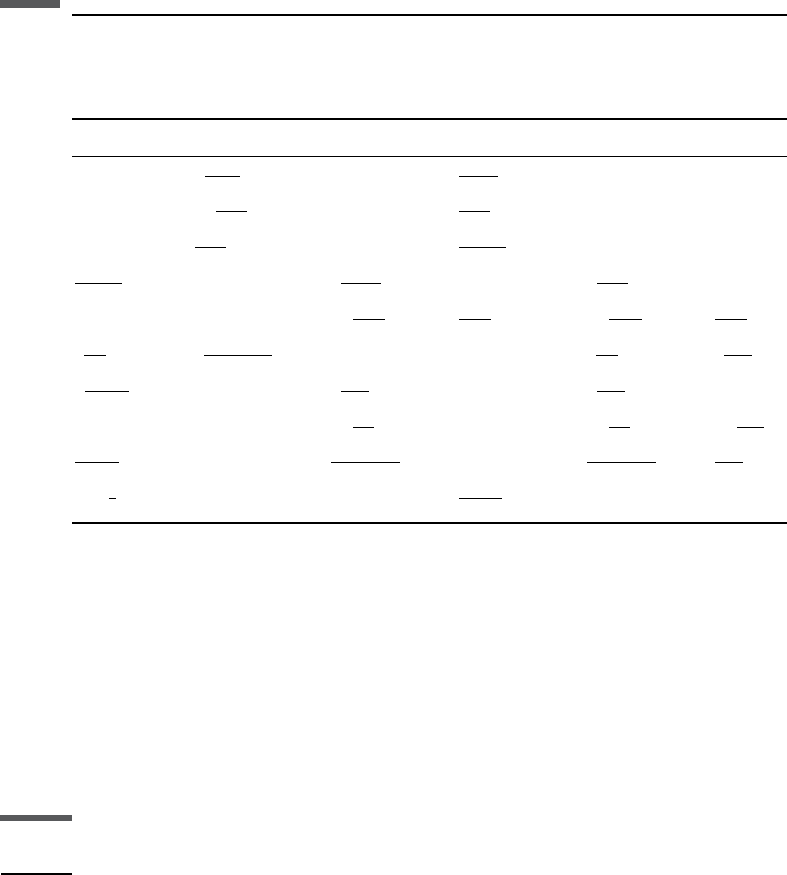
Table 2.1.1 summarizes useful relations among the constants of linear isotropic

elastic media.

Assumptions and limitations

The preceding equations assume isotropic, linear elastic media.

2.2 Anisotropic form of Hooke’s law

Synopsis

Hooke’s law for a general anisotropic, linear, elastic solid states that the stress s

linearly proportional to the strain e

, as expressed by



¼ c

ijkl

in which summation (over 1, 2, 3) is implied over the repeated subscripts k and l. The

elastic stiffness tensor, with elements c

ijkl

, is a fourth-rank tensor obeying the laws of

tensor transformation and has a total of 81 components. However, not all 81 com-

ponents are independent. The symmetry of stresses and strains implies that

ijkl

¼ c

jikl

¼ c

ijlk

¼ c

jilk

Table 2.1.1 Relationships among elastic constants in an isotropic material

(after Birch, 1961).

KE l vMm

l þ 2m/3 m

3lþ2m

lþm

—

2ðlþmÞ

l þ 2m —

—9K

Kl

3Kl

—

3Kl

3K–2l 3(K – l)/2

—

9Km

3Kþm

K–2m/3

3K2m

2ð3KþmÞ

K þ 4m/3 —

3ð3mEÞ

— m

E2m

ð3mEÞ

E/(2m)–1 m

4mE

3mE

—

—— 3K

3KE

9KE

3KE

3KþE

9KE

3KE

9KE

1þn

ð1þnÞð12nÞ

——l

1n

12n

2ð1þnÞ

3ð12nÞ

2m(1 þ v) m

12n

— m

22n

12n

—

—3K(1 – 2v)3K

1þn

—3K

1n

1þn

12n

2þ2n

3ð12nÞ

—

ð1þnÞð12nÞ

—

Eð1nÞ

ð1þnÞð12nÞ

2þ2n

M 

m — M  2m

M2m

2ðMmÞ

——

23 2.2 Anisotropic form of Hooke’s law

reducing the number of independent constants to 36. In addition, the existence of a

unique strain energy potential requires that

ijkl

¼ c

klij

further reducing the number of independent constants to 21. This is the maximum

number of independent elastic constants that any homogeneous linear elastic medium

can have. Additional restrictions imposed by symmetry considerations reduce the

number much further. Isotropic, linear elastic materials, which have maximum

symmetry, are completely characterized by two independent constants, whereas

materials with triclinic symmetry (the minimum symmetry) require all 21 constants.

Alternatively, the strains may be expressed as a linear combination of the stresses

by the following expression:

¼ s

ijkl



In this case s

ijkl

are elements of the elastic compliance tensor which has the same

symmetry as the corresponding stiffness tensor. The compliance and stiffness are

tensor inverses, denoted by

ijkl

klmn

¼ I

ijmn

ðd

þ d

The stiffness and compliance tensors must always be positive definite. One way to

express this requirement is that all of the eigenvalues of the elasticity tensor

(described below) must be positive.

Voigt notation

It is a standard practice in elasticity to use an abbreviated Voigt notation for the

stresses, strains, and stiffness and compliance tensors, for doing so simplifies some of

the key equations (Auld, 1990). In this abbreviated notation, the stresses and strains

are written as six-element column vectors rather than as nine-element square

matrices:

T ¼



¼ 



¼ 



¼ 



¼ 



¼ 



¼ 

E ¼

¼ e

¼ 2e

Note the factor of 2 in the definitions of strains, but not in the definition of stresses.

With the Voigt notation, four subscripts of the stiffness and compliance tensors are

reduced to two. Each pair of indices ij(kl) is replaced by one index I(J) using the

following convention:

24 Elasticity and Hooke’s law

ijðklÞ IðJÞ

11 1

22 2

33 3

23; 32 4

13; 31 5

12; 21 6

The relation, therefore, is c

¼ c

ijkl

and s

¼ s

ijkl

N, where

N ¼

1 for I and J ¼ 1; 2; 3

2 for I or J ¼ 4; 5; 6

4 for I and J ¼ 4; 5; 6

Note how the definition of s

differs from that of c

. This results from the factors

of 2 introduced in the definition of strains in the abbreviated notation. Hence the

Voigt matrix representation of the elastic stiffness is

and similarly, the Voigt matrix representation of the elastic compliance is

The Voigt stiffness and compliance matrices are symmetric. The upper triangle

contains 21 constants, enough to contain the maximum number of independent

constants that would be required for the least symmetric linear elastic material.

Using the Voigt notation, we can write Hooke’s law as



25 2.2 Anisotropic form of Hooke’s law

It is very important to note that the stress (strain) vector and stiffness (compliance)

matrix in Voigt notation are not tensors.

Caution

Some forms of the abbreviated notation adopt different definitions of strains, mov-

ing the factors of 2 and 4 from the compliances to the stiffnesses. However,

the form given above is the more common convention. In the two-index notation,

and s

can conveniently be represented as 6 6 matrices. However, these

matrices no longer follow the laws of tensor transformation. Care must be taken

when transforming from one coordinate system to another. One way is to go back

to the four-index notation and then use the ordinary laws of coordinate transform-

ation. A more efficient method is to use the Bond transformation matrices,

which are explained in Section 1.4 on coordinate transformations.

Voigt stiffness matrix structure for common anisotropy classes

The nonzero components of the more symmetric anisotropy classes commonly used

in modeling rock properties are given below in Voigt notation.

Isotropic: two independent constants

The structure of the Voigt elastic stiffness matrix for an isotropic linear elastic

material has the following form:

000

000c

0000c

00000c

; c

¼ c

 2c

The relations between the elements c and Lame

’s parameters l and m of isotropic

linear elasticity are

¼ l þ 2m; c

¼ l; c

¼ m

The corresponding nonzero isotropic compliance tensor elements can be written in

terms of the stiffnesses:

þ c

 c

ðÞc

þ 2c

ðÞ

; s

Energy considerations require that for an isotropic linear elastic material the

following conditions must hold:

K ¼ c



> 0; m ¼ c

> 0

26 Elasticity and Hooke’s law