Mavko G., Mukerji T., Dvorkin J. The Rock Physics Handbook
Подождите немного. Документ загружается.


Deformation of spherical shells
The radial displacement u
r
of a spherical elastic shell (Figure 2.9.3) with inner pore
radius R
p
and outer radius R
c
under applied confining pressure P
c
and pore pressure
P
p
is given by (Ciz et al., 2008)
u
r
¼
r
3Kð1 Þ
ðP
p
P
c
Þþ
R
3
p
4r
2
mð1 Þ
ðP
p
P
c
Þ
where r is the radial distance from the center of the sphere, K is the bulk modulus of
the solid elastic material, m is the shear modulus of the solid elastic material, and f is
the porosity. The associated volume change of the inner spherical pore is
dV
¼
3V
1
3K
þ
1
4m
dP
p
1
3K
þ
1
4m
dP
c
:
The volume change of the total sphere (shell plus pore) is
dV ¼
3V
1
1
3K
þ
1
4m
dP
p
1
3K
þ
4m
dP
c
:
Similarly, the radial displacement of a double-layer sphere (Figure 2.9.3) is given
by (Ciz et al., 2008)
u
r
¼
A
n
r
3
þ
B
n
r
2
where R
p
is the pore radius, R
c
is the outer sphere radius, and R
i
is the radius at the
boundary between the inner and outer elastic shells. The elastic moduli of the inner
solid shell are K
1
and m
1
, and the moduli of the outer shell are K
2
and m
2
:
A
1
¼
1
ð4m
1
m
2
þ 3K
2
m
2
ÞR
3
i
þð3K
2
m
1
3K
2
m
2
ÞR
3
c
R
3
p
P
p
n
ð3K
2
m
1
þ 4m
1
m
2
ÞR
3
c
R
3
i
P
c
o
R
p
R
c
R
i
R
p
R
c
Figure 2.9.3 Deformation of a single- and double-layer spherical shell.
67 2.9 Deformation of inclusions and cavities

B
1
¼
1
h
3
4
K
1
K
2
þ K
2
m
2
R
3
c
þðK
1
m
2
þ K
2
m
2
ÞR
3
i
i
R
3
p
R
3
i
P
p
n
3
4
K
1
K
2
þ K
1
m
2
R
3
c
R
3
i
R
3
p
P
c
o
A
2
¼
1
ð3K
1
m
1
3K
1
m
2
ÞR
3
p
ð3K
1
m
2
þ 4m
1
m
2
ÞR
3
i
hi
R
3
c
P
c
n
þð3K
1
m
2
4m
1
m
2
ÞR
3
i
R
3
p
P
p
o
B
2
¼
1
ðK
1
m
1
K
2
m
1
ÞR
3
1
3
4
K
1
K
2
þ K
2
m
1
R
3
p
hi
R
3
c
R
3
i
P
c
n
þ
3
4
K
1
K
2
þ K
1
m
1
R
3
c
R
3
i
R
3
p
P
p
o
¼ K
2
m
1
ð3K
1
þ 4m
2
ÞR
3
c
R
3
i
K
1
m
2
ð3K
2
þ 4m
1
ÞR
3
i
R
3
p
þ 4m
1
m
2
ðK
1
K
2
ÞR
6
i
þ 3K
1
K
2
ðm
2
m
1
ÞR
3
c
R
3
p
Uses
The equations presented in this section are useful for computing deformation of
cavities in elastic solids and estimating effective moduli of porous solids.
Assumptions and limitations
The equations presented in this section are based on the following assumptions.
Solid material must be homogeneous, isotropic, linear, and elastic.
Results for specific geometries, such as spheres and ellipsoids, are derived for
single isolated cavities. Therefore, estimates of effective moduli based on these
are limited to relatively low pore concentrations where pore elastic interaction is
small.
Pore-pressure computations assume that the induced pore pressure is uniform
throughout the pore space, which will be the case if (1) there is only one pore,
(2) all pores are well connected and the frequency and viscosity are low enough for
any pressure differences to equilibrate, or (3) all pores have the same dry pore
stiffness.
2.10 Deformation of a circular hole: borehole stresses
Synopsis
Presented here are some solutions related to a circular hole in a stressed, linear,
elastic, and poroelastic isotropic medium.
68 Elasticity and Hooke’s law
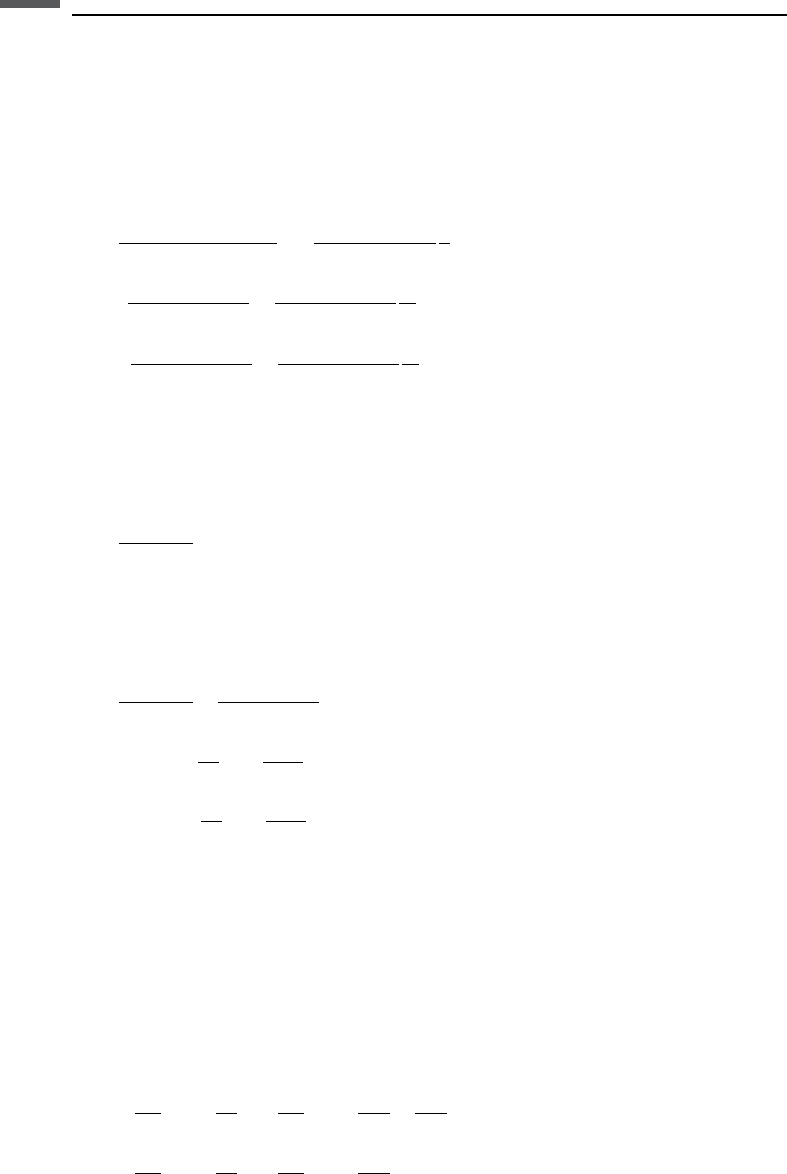
Hollow cylinder with internal and external pressures
The cylinder’s internal radius is R
1
and the external radius is R
2
. Hydrostatic stress p
1
is applied at the interior surface at R
1
and hydrostatic stress p
2
is applied at the
exterior surface at R
2
. The resulting (plane-strain) outward displacement U and radial
and tangential stresses are
U ¼
ðp
2
R
2
2
p
1
R
2
1
Þ
2ðl þ mÞðR
2
2
R
2
1
Þ
r þ
ðp
2
p
1
ÞR
2
1
R
2
2
2mðR
2
2
R
2
1
Þ
1
r
rr
¼
ðp
2
R
2
2
p
1
R
2
1
Þ
ðR
2
2
R
2
1
Þ
ðp
2
p
1
ÞR
2
1
R
2
2
ðR
2
2
R
2
1
Þ
1
r
2
yy
¼
ðp
2
R
2
2
p
1
R
2
1
Þ
ðR
2
2
R
2
1
Þ
þ
ðp
2
p
1
ÞR
2
1
R
2
2
ðR
2
2
R
2
1
Þ
1
r
2
where l and m are the Lame
´
coefficient and shear modulus, respectively.
If R
1
¼ 0, we have the case of a solid cylinder under external pressure, with
displacement and stress denoted by the following:
U ¼
p
2
r
2ðl þ mÞ
rr
¼
yy
¼ p
2
If, instead, R
2
!1, then
U ¼
p
2
r
2ðl þ mÞ
þ
ðp
2
p
1
ÞR
2
1
2mr
rr
¼ p
2
1
R
2
1
r
2
þ
p
1
R
2
1
r
2
yy
¼ p
2
1 þ
R
2
1
r
2
p
1
R
2
1
r
2
These results for plane strain can be converted to plane stress by replacing v by
v/(1 þ v), where v is the Poisson ratio.
Circular hole with principal stresses at infinity
The circular hole with radius R lies along the z-axis. A principal stress, s
xx
, is applied
at infinity. The stress solution is then
rr
¼
xx
2
1
R
2
r
2
þ
xx
2
1
4R
2
r
2
þ
3R
4
r
4
cos 2y
yy
¼
xx
2
1 þ
R
2
r
2
xx
2
1 þ
3R
4
r
4
cos 2y
69 2.10 Deformation of a circular hole: borehole stresses

ry
¼
xx
2
1 þ
2R
2
r
2
3R
4
r
4
sin 2y
8mU
r
R
xx
¼ð 1 þ 2 cos 2yÞ
r
R
þ
2R
r
1 þ þ 1
R
2
r
2
cos 2y
8mU
y
R
xx
¼
2r
R
þ
2R
r
1
R
2
r
2
sin 2y
where y is measured from the x-axis, and
¼ 3 4v; for plane strain
¼
3 v
1 þ v
; for plane stress
At the cavity surface, r ¼ R,
rr
¼
ry
¼ 0
yy
¼
xx
ð1 2 cos 2yÞ
Thus, we see the well-known result that the borehole creates a stress concentration of
s
yy
¼ 3s
xx
at y ¼ 90
.
Stress concentration around an elliptical hole
If, instead, the borehole is elliptical in cross-section with a shape denoted by
(Lawn and Wilshaw, 1975)
x
2
b
2
þ
y
2
c
2
¼ 1
where b is the semiminor axis and c is the semimajor axis, and the principal stress
s
xx
is applied at infinity, then the largest stress concentration occurs at the tip of the
long axis (y ¼ c; x ¼ 0). This is the same location at y ¼ 90
as for the circular hole.
The stress concentration is
yy
¼
xx
½1 þ 2ðc=Þ
1=2
where r is the radius of curvature at the tip given by
¼
b
2
c
When b c, the stress concentration is approximately
yy
xx
2c
b
¼ 2
ffiffiffi
c
r
70 Elasticity and Hooke’s law
Stress around an inclined cylindrical hole
We now consider the case of a cylindrical borehole of radius R inclined at an angle i
to the vertical axis, in a linear, isotropic elastic medium with Poisson ratio n in a
nonhydrostatic remote stress field (Jaeger and Cook, 1969; Bradley, 1979; Fjaer
et al., 2008). The borehole coordinate system is denoted by (x, y, z) with the z-axis
along the axis of the borehole. The remote principal stresses are denoted by
n
; the vertical stress;
H
; the maximum horizontal stress; and
h
; the minimum horizontal stress
The coordinate system for the remote stress field (shown in Figure 2.10.1) is denoted
by (x
0
, y
0
, z
0
) with x
0
along the direction of the maximum horizontal stress, and z
0
along
the vertical. The angle a represents the azimuth of the borehole x-axis with respect
to the x
0
-axis, while y is the azimuthal angle around the borehole measured from the
x-axis. Assuming plane-strain conditions with no displacements along the z-axis,
the stresses as a function of radial distance r and azimuthal angle y are given by
(Fjaer et al., 2008):
rr
¼
0
xx
þ
0
yy
2
!
1
R
2
r
2
þ
0
xx
0
yy
2
!
1 þ 3
R
4
r
4
4
R
2
r
2
cos 2y
þ
0
xy
1 þ 3
R
4
r
4
4
R
2
r
2
sin 2 y þ p
w
R
2
r
2
yy
¼
0
xx
þ
0
yy
2
!
1 þ
R
2
r
2
0
xx
0
yy
2
!
1 þ 3
R
4
r
4
cos 2y
0
xy
1 þ 3
R
4
r
4
sin 2y p
w
R
2
r
2
a
s
H
s
h
θ
s
v
x ⬘ x
y ⬘
y
z
z ⬘
i
Figure 2.10.1 The coordinate system for the remote stress field around an inclined, cylindrical
borehole.
71 2.10 Deformation of a circular hole: borehole stresses

zz
¼
0
zz
v 2
0
xx
0
yy
R
2
r
2
cos 2y þ 4
0
xy
R
2
r
2
sin 2y
ry
¼
0
yy
0
xx
2
!
1 3
R
4
r
4
þ 2
R
2
r
2
sin 2y þ
0
xy
1 3
R
4
r
4
þ 2
R
2
r
2
cos 2y
yz
¼
0
xz
sin y þ
0
yz
cos y
1 þ
R
2
r
2
rz
¼
0
xz
cos y þ
0
yz
sin y
1
R
2
r
2
In the above equations p
w
represents the well-bore pressure and
0
ij
is the remote
stress tensor expressed in the borehole coordinate system through the usual coordin-
ate transformation (see Section 1.4 on coordinate transformations) involving the
direction cosines of the angles between the (x
0
, y
0
, z
0
) axes and the (x, y, z) axes as
follows:
0
xx
¼ b
2
xx
0
H
þ b
2
xy
0
h
þ b
2
xz
0
n
0
yy
¼ b
2
yx
0
H
þ b
2
yy
0
h
þ b
2
yz
0
n
0
zz
¼ b
2
zx
0
H
þ b
2
zy
0
h
þ b
2
zz
0
n
0
xy
¼ b
xx
0
b
yx
0
H
þ b
xy
0
b
yy
0
h
þ b
xz
0
b
yz
0
n
0
yz
¼ b
yx
0
b
zx
0
H
þ b
yy
0
b
zy
0
h
þ b
yz
0
b
zz
0
n
0
zx
¼ b
zx
0
b
xx
0
H
þ b
zy
0
b
xy
0
h
þ b
zz
0
b
xz
0
n
and
b
xx
0
¼ cos a cos i;
b
yx
0
¼sin a;
b
zx
0
¼ cos a sin i;
b
xy
0
¼ sin a cos i ;
b
yy
0
¼ cos a;
b
zy
0
¼ sin a sin i;
b
xz
0
¼sin i
b
yz
0
¼ 0
b
zz
0
¼ cos i
Stress around a vertical cylindrical hole in a poroelastic medium
The circular hole with radius R
i
lies along the z-axis. Pore pressure, p
f
, at the
permeable borehole wall equals the pressure in the well bore, p
w
. At a remote
boundary R
0
R
i
the stresses and pore pressure are
zz
ðR
0
Þ¼
n
rr
ðR
0
Þ¼
yy
ðR
0
Þ¼
h
p
f
ðR
0
Þ¼p
f0
72 Elasticity and Hooke’s law
The stresses as a function of radial distance r from the hole are given by (Risnes et al.,
1982; Bratli et al., 1983; Fjaer et al., 2008)
rr
¼
h
þð
h
p
w
Þ
R
2
i
R
2
0
R
2
i
1
R
0
r
2
"#
ðp
f0
p
w
Þ
1 2n
2ð1 nÞ
a
R
2
i
R
2
0
R
2
i
1
R
0
r
2
"#
þ
lnðR
0
=rÞ
lnðR
0
=R
i
Þ
()
yy
¼
h
þð
h
p
w
Þ
R
2
i
R
2
0
R
2
i
1 þ
R
0
r
2
"#
ðp
f0
p
w
Þ
1 2n
2ð1 nÞ
a
R
2
i
R
2
0
R
2
i
1 þ
R
0
r
2
"#
þ
lnðR
0
=rÞ1
lnðR
0
=R
i
Þ
()
zz
¼
n
þ 2nð
h
p
w
Þ
R
2
i
R
2
0
R
2
i
ðp
f0
p
w
Þ
1 2n
2ð1 nÞ
an
2R
2
i
R
2
0
R
2
i
þ
2lnðR
0
=rÞn
lnðR
0
=R
i
Þ
where n is the dry (drained) Poisson ratio of the poroelastic medium, a ¼ 1 K
dry
=K
0
is the Biot coefficient, K
dry
is effective bulk modulus of dry porous solid, and K
0
is
the bulk modulus of solid mineral material. In the limit R
0
=R
i
!1the expressions
simplify to (Fjaer et al., 2008)
rr
¼
h
ð
h
p
w
Þ
R
i
r
2
þðp
f0
p
w
Þ
1 2n
2ð1 nÞ
a
R
i
r
2
lnðR
0
=rÞ
lnðR
0
=R
i
Þ
"#
yy
¼
h
þð
h
p
w
Þ
R
i
r
2
ðp
f0
p
w
Þ
1 2n
2ð1 n Þ
a
R
i
r
2
þ
lnðR
0
=rÞ
lnðR
0
=R
i
Þ
"#
zz
¼
n
ðp
f0
p
w
Þ
1 2n
2ð1 nÞ
a
2lnðR
0
=rÞn
lnðR
0
=R
i
Þ
Uses
The equations presented in this section can be used for the following:
estimating the stresses around a borehole resulting from tectonic stresses;
estimating the stresses and deformation of a borehole caused by changes in
borehole fluid pressure.
Assumptions and limitations
The equations presented in this section are based on the following assumptions:
the material is linear, isotropic, and elastic or poroelastic.
73 2.10 Deformation of a circular hole: borehole stresses

Extensions
More complicated remote stress fields can be constructed by superimposing the
solutions for the corresponding principal stresses.
2.11 Mohr’s circles
Synopsis
Mohr’s circles provide a graphical representation of how the tractions on a plane
depend on the angular orientation of the plane within a given stress field. Consider a
stress state with principal stresses s
1
s
2
s
3
and coordinate axes defined
along the corresponding principal directions x
1
, x
2
, x
3
. The traction vector, T, acting
on a plane with outward unit normal vector, n ¼ (n
1
, n
2
, n
3
), is given by Cauchy’s
formula as
T ¼ sn
where s is the stress tensor. The components of n are the direction cosines of
n relative to the coordinate axes and are denoted by
n
1
¼ cos ; n
2
¼ cos g; n
3
¼ cos y
and
n
2
1
þ n
2
2
þ n
2
3
¼ 1
where f, g, and y are the angles between n and the axes x
1
, x
2
, x
3
(Figure 2.11.1).
x
3
x
1
x
2
n
T
q
f
g
Figure 2.11.1 Angle and vector conventions for Mohr’s circles.
74 Elasticity and Hooke’s law

The normal component of traction, s, and the magnitude of the shear component,
t, acting on the plane are given by
¼ n
2
1
1
þ n
2
2
2
þ n
2
3
3
t
2
¼ n
2
1
2
1
þ n
2
2
2
2
þ n
2
3
2
3
2
Three-dimensional Mohr’s circle
The numerical values of s and t can be read graphically from the three-dimensional
Mohr’s circle shown in Figure 2.11.2. All permissible values of s and t must lie in the
shaded area.
To determine s and t from the orientation of the plane (f, g, and y), perform the
following procedure.
(1) Plot s
1
s
2
s
3
on the horizontal axis and construct the three circles, as shown.
The outer circle is centered at (s
1
þ s
3
)/2 and has radius (s
1
– s
3
)/2. The
left-hand inner circle is centered at (s
2
þ s
3
)/2 and has radius (s
2
– s
3
)/2. The
right-hand inner circle is centered at (s
1
þ s
2
)/2 and has radius (s
1
– s
2
)/2.
(2) Mark angles 2y and 2f on the small circles centered at A and B. For example,
f ¼ 60
plots at 2f ¼ 120
from the horizontal, and y ¼ 75
plots at 2y ¼ 150
from the horizontal, as shown. Be certain to include the factor of 2, and note the
different directions defined for the positive angles.
(3) Draw a circle centered at point A that intersects the right-hand small circle at the
mark for f.
(4) Draw another circle centered at point B that intersects the left-hand small circle
at the point for y.
(5) The intersection of the two constructed circles at point P gives the values of
s and t.
Reverse the procedure to determine the orientation of the plane having particular
values of s and t.
15⬚
30⬚
30⬚
45⬚
45⬚
60⬚
60⬚
75⬚
75⬚
A
B
P
Figure 2.11.2 Three-dimensional Mohr’s circle.
75 2.11 Mohr’s circles
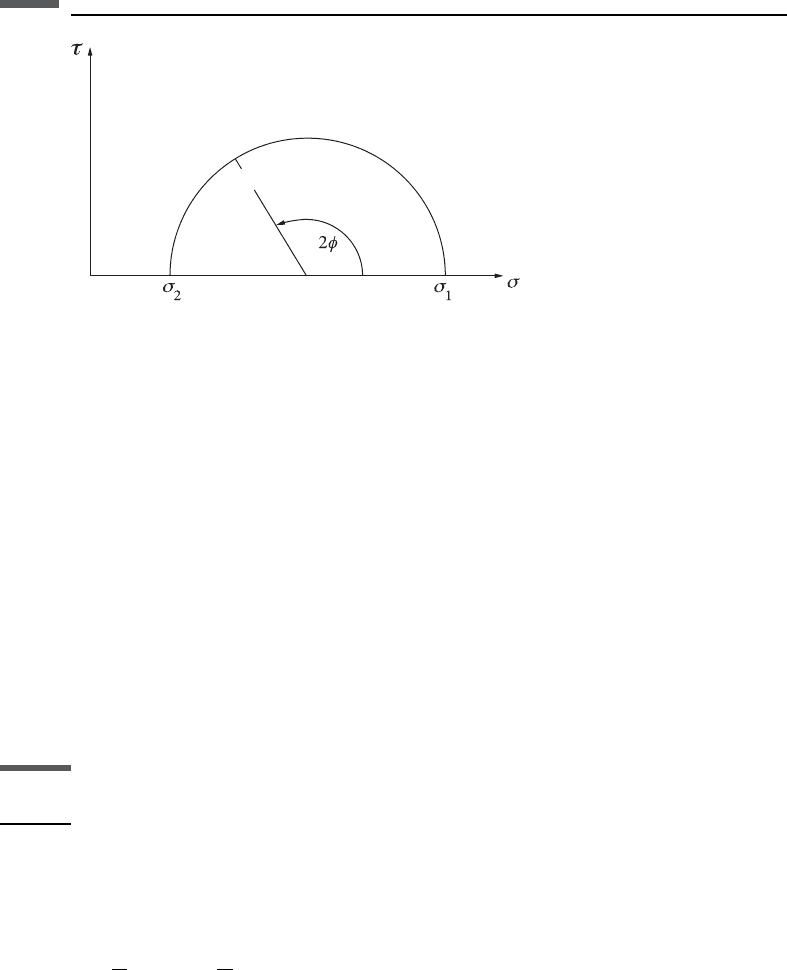
Two-dimensional Mohr’s circle
When the plane of interest contains one of the principal axes, the tractions on the
plane depend only on the two remaining principal stresses, and using Mohr’s circle is
therefore simplified. For example, when y ¼ 90
(i.e., the x
3
-axis lies in the plane of
interest), all stress states lie on the circle centered at B in Figure 2.11.2. The stresses
then depend only on s
1
and s
2
and on the angle f, and we need only draw the single
circle, as shown in Figure 2.11.3.
Uses
Mohr’s circle is used for graphical determination of normal and shear tractions acting
on a plane of arbitrary orientation relative to the principal stresses.
2.12 Static and dynamic moduli
In a uniaxial stress experiment (Figure 2.12.1), Young’s modulus E is defined as
the ratio of the axial stress s to the axial strain e
a
, while Poisson’s ratio n is defined
as the (negative) ratio of the radial strain e
r
to the axial strain:
E ¼
e
a
; n ¼
e
r
e
a
It follows from these definitions that Poisson’s ratio is zero if the sample does not
expand radially during axial loading and Poisson’s ratio is 0.5 if the radial strain is
half the axial strain, which is the case for fluids and incompressible solids. Poisson’s
ratio must lie within the range 1 < n 0:5.
The speeds of elastic waves in the solid are linked to the elastic moduli and the
bulk density r by the wave equation. The corresponding expressions for Poisson’s
ratio and Young’s modulus are:
P
30⬚
f =158
45⬚
60⬚
75⬚
Figure 2.11.3 Two-dimensional Mohr’s circle.
76 Elasticity and Hooke’s law
