Mavko G., Mukerji T., Dvorkin J. The Rock Physics Handbook
Подождите немного. Документ загружается.

I
P
¼ V
P
I
S
¼ V
S
where I
P
, I
S
are P- and S-wave impedances, V
P
, V
S
are P- and S-wave velocities, and
r is density.
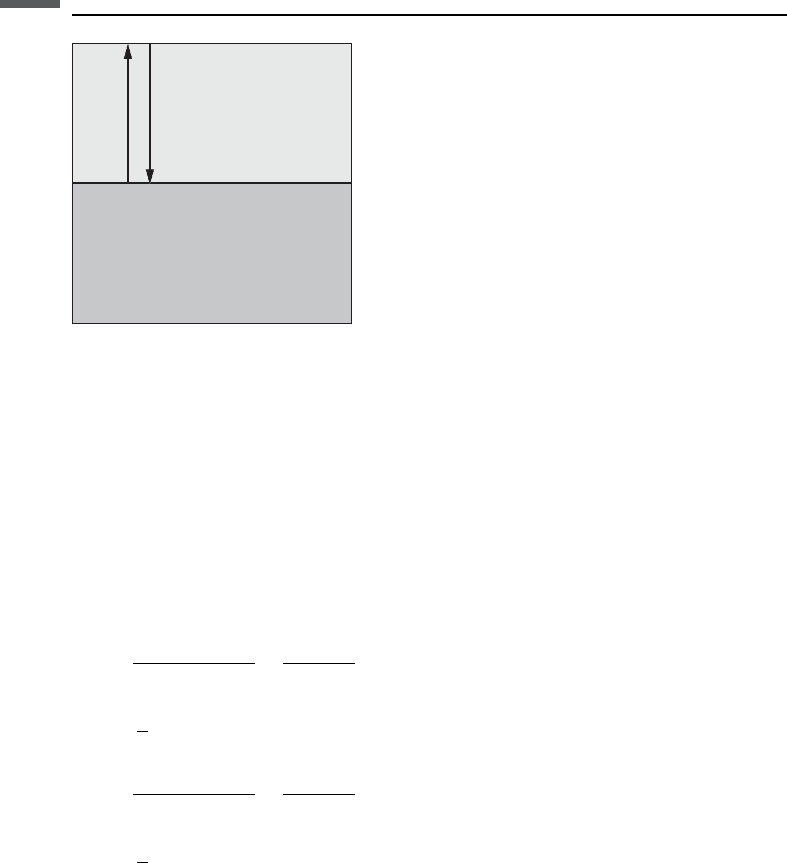
At an interface between two thick homogeneous, isotropic, elastic layers, the
normal incidence reflectivity, defined as the ratio of the reflected wave amplitude
to the incident wave amplitude, is
R
PP
¼
2
V
P2
1
V
P1
2
V
P2
þ
1
V
P1
¼
I
P2
I
P1
I
P2
þ I
P1
1
2
lnðI
P2
=I
P1
Þ
R
SS
¼
2
V
S2
1
V
S1
2
V
S2
þ
1
V
S1
¼
I
S2
I
S1
I
S2
þ I
S1
1
2
lnðI
S2
=I
S1
Þ
where R
PP
is the normal incidence P-to-P reflectivity, R
SS
is the S-to-S reflectivity,
and the subscripts 1 and 2 refer to the first and second media, respectively
(Figure 3.5.1). The logarithmic approximation is reasonable for |R| < 0.5 (Castagna,
1993). A normally incident P-wave generates only reflected and transmitted P-waves.
A normally incident S-wave generates only reflected and transmitted S-waves. There
is no mode conversion.
AVO: amplitude variations with offset
For non-normal incidence, the situation is more complicated. An incident P-wave
generates reflected P- and S-waves and transmitted P- and S-waves. The reflection
r
1
⬘
V
1
r
2
⬘
V
2
Figure 3.5.1 Reflection of a normal-incidence wave at an interface between two thick
homogeneous, isotropic, elastic layers.
97 3.5 Reflectivity and AVO in isotropic media

and transmission coefficients depend on the angle of incidence as well as on the
material properties of the two layers. An excellent review is given by Castagna
(1993).
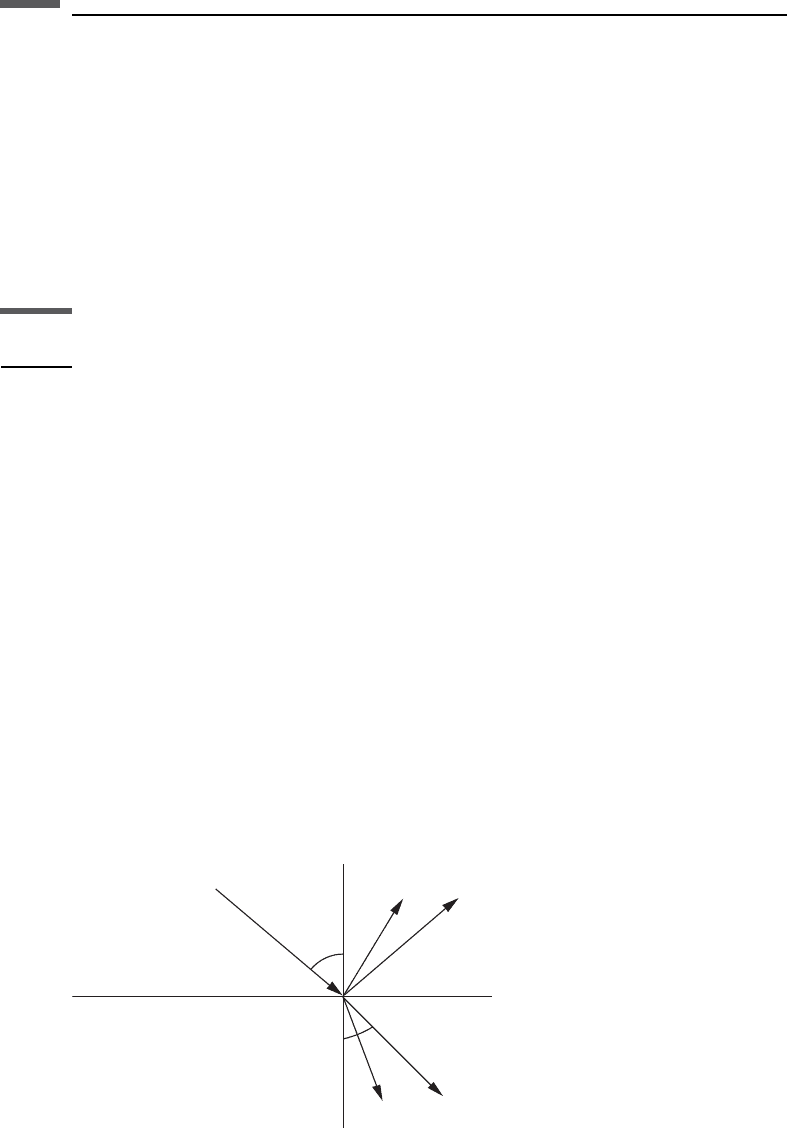
The angles of the incident, reflected, and transmitted rays (Figure 3.5.2) are related
by Snell’s law as follows:
p ¼
sin
1
V
P1
¼
sin
2
V
P2
¼
sin
S1
V
S1
¼
sin
S2
V
S2
where p is the ray parameter. y and y
S
are the angles of P- and S-wave propagation,
respectively, relative to the reflector normal. Subscripts 1 and 2 indicate angles or
material properties of layers 1 and 2, respectively.
The complete solution for the amplitudes of transmitted and reflected P- and
S-waves for both incident P- and S-waves is given by the Knott–Zoeppritz equations
(Knott, 1899; Zoeppritz, 1919; Aki and Richards, 1980; Castagna, 1993).
Aki and Richards ( 1980) give the results in the following convenient matrix form:
PP
#"
SP
#"
PP
""
SP
""
PS
#"
SS
#"
PS
""
SS
""
PP
##
SP
##
PP
"#
SP
"#
PS
##
SS
##
PS
"#
SS
"#
0
B
B
B
B
B
B
B
@
1
C
C
C
C
C
C
C
A
¼ M
1
N
where each matrix element is a reflection or transmission coefficient for displacement
amplitudes. The first letter designates the type of incident wave, and the second letter
designates the type of reflected or transmitted wave. The arrows indicate downward #
and upward ↑ propagation, so that a combination #" indicates a reflection coefficient,
while a combination ## indicates a transmission coefficient. The matrices M and N
are given by
V
P1
, V
S1
, r
1
V
P2
, V
S2
, r
2
q
2
q
S2
Reflected
P-wave
Incident
P-wave
Reflected
S-wave
Transmitted
P-wave
q
S1
q
1
Transmitted
S-wave
Figure 3.5.2 The angles of the incident, reflected, and transmitted rays of a P-wave
with non-normal incidence.
98 Seismic wave propagation
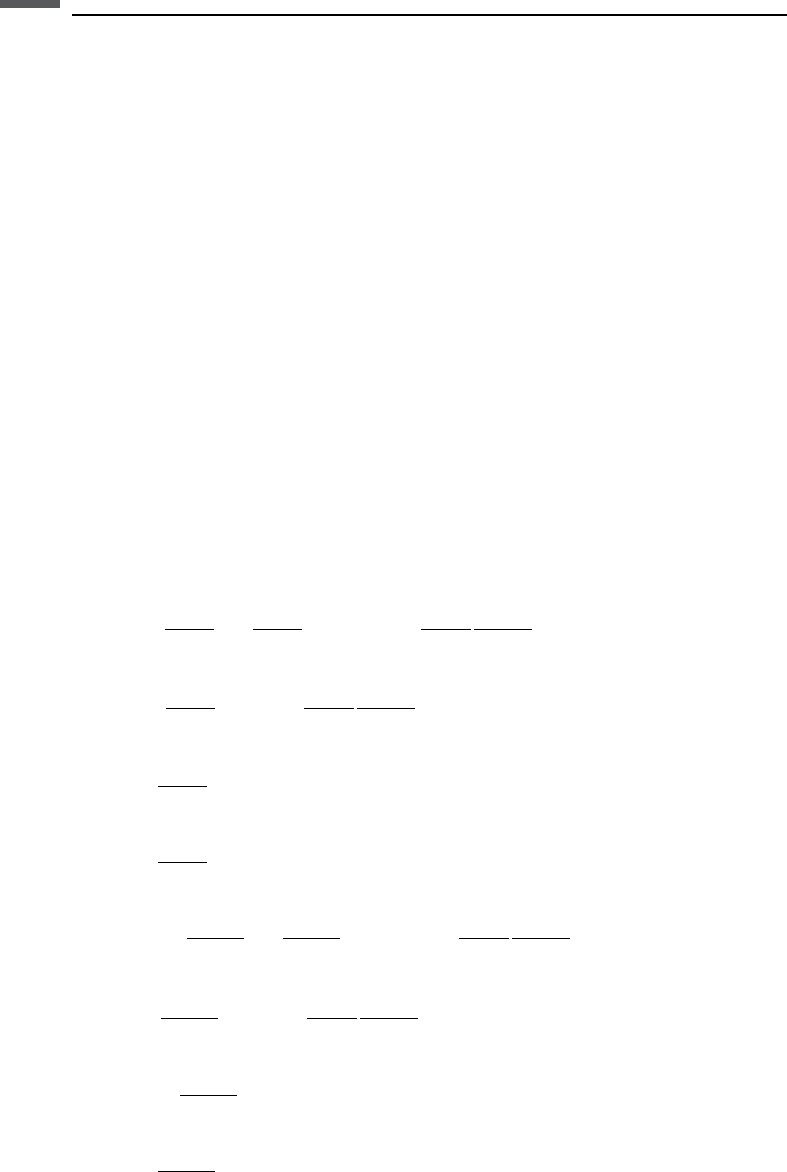
M ¼
sin
1
cos
S1
sin
2
cos
S2
cos
1
sin
S1
cos
2
sin
S2
2
1
V
S1
sin
S1
cos
1
1
V
S1
1 2 sin
2
S1
2
2
V
S2
sin
S2
cos
2
2
V
S2
1 2 sin
2
S2
1
V
P1
1 2 sin
2
S1
1
V
S1
sin 2
S1
2
V
P2
1 2 sin
2
S2
2
V
S2
sin 2
S2
0
B
B
B
B
B
B
B
B
@
1
C
C
C
C
C
C
C
C
A
N ¼
sin
1
cos
S1
sin
2
cos
S2
cos
1
sin
S1
cos
2
sin
S2
2
1
V
S1
sin
S1
cos
1
1
V
S1
1 2 sin
2
S1
2
2
V
S2
sin
S2
cos
2
2
V
S2
1 2 sin
2
S2
1
V
P1
1 2 sin
2
S1
1
V
S1
sin 2
S1
2
V
P2
1 2 sin
2
S2
2
V
S2
sin 2
S2
0
B
B
B
B
B
B
B
B
@
1
C
C
C
C
C
C
C
C
A
Results for incident P and incident S, given explicitly by Aki and Richards (1980),
are as follows, where R
PP
¼ PP
#"
; R
PS
¼ PS
#"
; T
PP
¼ PP
##
; T
PS
¼ PS
##
; R
SS
¼ SS
#"
; R
SP
¼ SP
#"
;
T
SP
¼ SP
##
; T
SS
¼ SS
##
:
R
PP
¼ b
cos
1
V
P1
c
cos
2
V
P2
F a þ d
cos
1
V
P1
cos
S2
V
S2
Hp
2
.
D
R
PS
¼2
cos
1
V
P1
ab þ cd
cos
2
V
P2
cos
S2
V
S2
pV
P1
.
V
S1
DðÞ
T
PP
¼2
1
cos
1
V
P1
FV
P1
= V
P2
DðÞ
T
PS
¼2
1
cos
1
V
P1
HpV
P1
= V
S2
D
ðÞ
R
SS
¼ b
cos
S1
V
S1
c
cos
S2
V
S2
E a þ d
cos
2
V
P2
cos
S1
V
S1
Gp
2
.
D
R
SP
¼2
cos
S1
V
S1
ab þ cd
cos
2
V
P2
cos
S2
V
S2
pV
S1
= V
P1
DðÞ
T
SP
¼2
1
cos
S1
V
S1
GpV
S1
= V
P2
DðÞ
T
SS
¼2
1
cos
S1
V
S1
EV
S1
= V
S2
DðÞ
99 3.5 Reflectivity and AVO in isotropic media

where
a ¼
2
1 2 sin
2
S2
1
1 2 sin
2
S1
b ¼
2
1 2 sin
2
S2
þ 2
1
sin
2
S1
c ¼
1
1 2 sin
2
S1
þ 2
2
sin
2
S2
d ¼ 2
2
V
2
S2
1
V
2
S1
D ¼ EF þ GHp
2
¼ det MðÞ= V
P1
V
P2
V
S1
V
S2
ðÞ
E ¼ b
cos
1
V
P1
þ c
cos
2
V
P2
F ¼ b
cos
S1
V
S1
þ c
cos
S2
V
S2
G ¼ a d
cos
1
V
P1
cos
S2
V
S2
H ¼ a d
cos
2
V
P2
cos
S1
V
S1
and p is the ray parameter.
Approximate forms
Although the complete Zoeppritz equations can be evaluated numerically, it is often
useful and more insightful to use one of the simpler approximations.
Bortfeld (1961) linearized the Zoeppritz equations by assuming small contrasts
between layer properties as follows:
R
PP
ð
1
Þ
1
2
ln
V
P2
2
cos
1
V
P1
1
cos
2
þ
sin
1
V
P1
2
ðV
2
S1
V
2
S2
Þ 2 þ
lnð
2
=
1
Þ
lnðV
S2
=V
S1
Þ
Aki and Richards (1980) also derived a simplified form by assuming small layer
contrasts. The results are conveniently expressed in terms of contrasts in V
P
, V
S
, and
r as follows:
R
PP
ðÞ
1
2
1 4p
2
V
2
S
þ
1
2 cos
2
V
P
V
P
4p
2
V
2
S
V
S
V
S
R
PS
ðÞ
p
V
P
2 cos
S
1 2
V
2
S
p
2
þ 2
V
2
S
cos
V
P
cos
S
V
S
4p
2
V
2
S
4
V
2
S
cos
V
P
cos
S
V
S
V
S
V
S
T
PP
ðÞ1
1
2
þ
1
2 cos
2
1
V
P
V
P
100 Seismic wave propagation
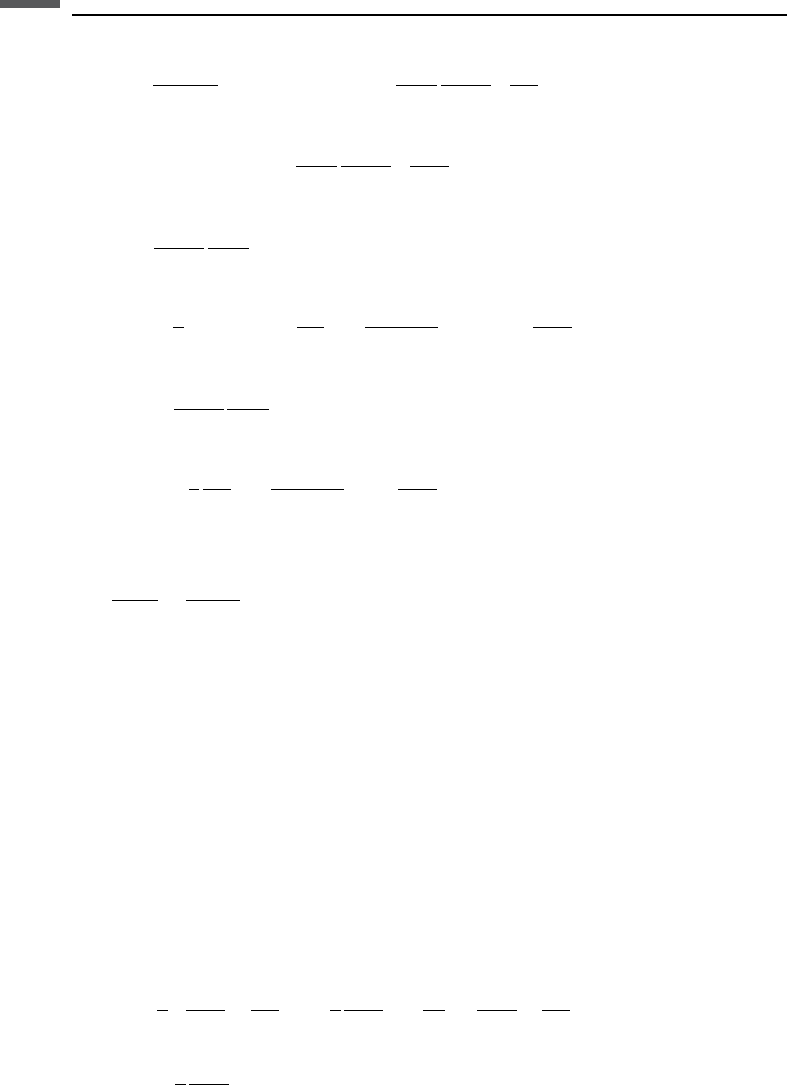
T
PS
ðÞ
p
V
P
2 cos
S
1 2
V
2
S
p
2
2
V
2
S
cos
V
P
cos
S
V
S
4p
2
V
2
S
þ 4
V
2
S
cos
V
P
cos
S
V
S
V
S
V
S
R
SP
ðÞ
cos
S
V
P
V
S
cos
R
PS
ðÞ
R
SS
ðÞ
1
2
1 4p
2
V
2
S
1
2 cos
2
S
4p
2
V
2
S
V
S
V
S
T
SP
ðÞ
cos
S
V
P
V
S
cos
T
PS
T
SS
ðÞ1
1
2
þ
1
2 cos
2
S
1
V
S
V
S
where
p ¼
sin
1
V
P1
¼
sin
S1
V
S1
¼
2
1
V
P
¼ V
P2
V
P1
V
S
¼ V
S2
V
S1
¼
2
þ
1
ðÞ=2
S
¼
S2
þ
S1
ðÞ=2
¼
2
þ
1
ðÞ=2
V
P
¼ V
P2
þ V
P1
ðÞ=2
V
S
¼ V
S2
þ V
S1
ðÞ=2
Often, the mean P-wave angle y is approximated as y
1
, the P-wave angle of
incidence.
The result for P-wave reflectivity can be rewritten in the familiar form:
R
PP
ðÞR
P0
þ B sin
2
þ Cðtan
2
sin
2
Þ
or
R
PP
ðÞ
1
2
V
P
V
P
þ
þ
1
2
V
P
V
P
2
V
2
S
V
2
P
2
V
S
V
S
þ
sin
2
þ
1
2
V
P
V
P
tan
2
sin
2
This form can be interpreted in terms of different angular ranges (Castagna, 1993).
In the above equations R
P0
is the normal incidence reflection coefficient as
expressed by
101 3.5 Reflectivity and AVO in isotropic media
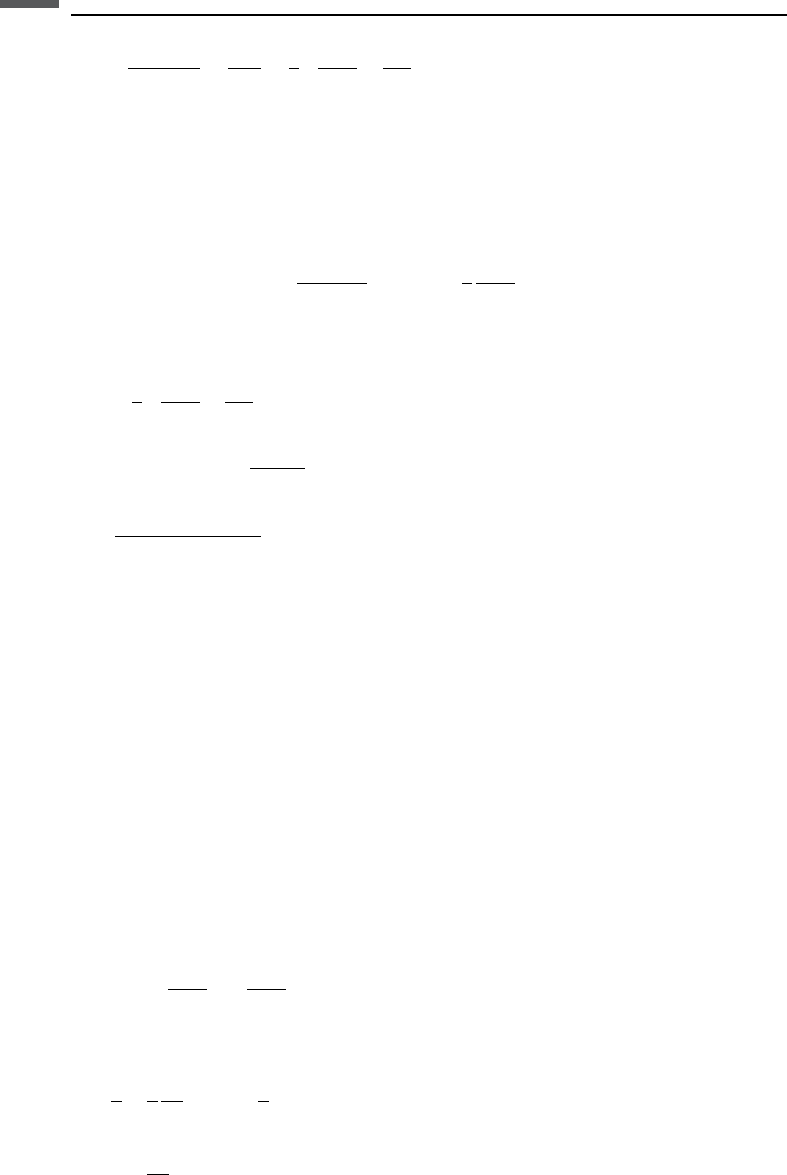
R
P0
¼
I
P2
I
P1
I
P2
þ I
P1
I
P
2I
P
1
2
V
P
V
P
þ
The parameter B describes the variation at intermediate offsets and is often called the
AVO gradient, and C dominates at far offsets near the critical angle.
Shuey (1985) presented a similar approximation where the AVO gradient is
expressed in terms of the Poisson ratio n as follows:
R
PP
1
ðÞR
P0
þ ER
P0
þ
n
1
nðÞ
2
"#
sin
2
1
þ
1
2
V
P
V
P
tan
2
1
sin
2
1
where
R
P0
1
2
V
P
V
P
þ
E ¼ F 21þ FðÞ
1 2
n
1
n
F ¼
V
P
=
V
P
V
P
=
V
P
þ =
and
n ¼ n
2
n
1
n ¼ n
2
þ n
1
ðÞ=2
The coefficients E and F used here in Shuey’s equation are not the same as those
defined earlier in the solutions to the Zoeppritz equations.
Smith and Gidlow (1987) offered a further simplification to the Aki–Richards
equation by removing the dependence on density using Gardner’s equation (see
Section 7.10) as follows:
/ V
1=4
giving
R
PP
ðÞc
V
P
V
P
þ d
V
S
V
S
where
c ¼
5
8
1
2
V
2
S
V
2
P
sin
2
þ
1
2
tan
2
d ¼4
V
2
S
V
2
P
sin
2
102 Seismic wave propagation

Wiggins et al. (1983) showed that when V
P
2V
S
, the AVO gradient is approxi-
mately (Spratt et al., 1993)
B R
P0
2R
S0
given that the P and S normal incident reflection coefficients are
R
P0
1
2
V
P
V
P
þ
R
S0
1
2
V
S
V
S
þ
Hilterman (1989) suggested the following slightly modified form:
R
PP
ðÞR
P0
cos
2
þ PR sin
2
where R
P0
is the normal incidence reflection coefficient and
PR ¼
n
2
n
1
1
nðÞ
2
This modified form has the interpretation that the near-offset traces reveal the P-wave
impedance, and the intermediate-offset traces image contrasts in Poisson ratio
(Castagna, 1993).
Gray et al. (1999) derived linearized expressions for P–P reflectivity in terms of the
angle of incidence, y, and the contrast in bulk modulus, K, shear modulus, m, and bulk
density, r:
R ðÞ¼
1
4
1
3
V
2
S
V
2
P
sec
2
K
K
þ
V
2
S
V
2
P
1
3
sec
2
2 sin
2
þ
1
2
1
4
sec
2
Similarly, their expression in terms of Lame
´
’s coefficient, l, shear modulus, and bulk
density is
R ðÞ¼
1
4
1
2
V
2
S
V
2
P
sec
2
l
l
þ
V
2
S
V
2
P
1
2
sec
2
2 sin
2
þ
1
2
1
4
sec
2
In the same assumptions of small layer contrast and limited angle of incidence, we
can write the linearized SV-to-SV reflection (Ru
¨
ger, 2001):
R
SV-iso
S
ðÞ
1
2
I
S
I
S
þ
7
2
V
S
V
S
þ 2
sin
2
S
1
2
V
S
V
S
sin
2
S
tan
2
S
103 3.5 Reflectivity and AVO in isotropic media

where y
S
is the SV-wave phase angle of incidence and I
S
¼ V
S
is the shear
impedance.
Similarly, for SH-to-SH reflection (Ru
¨
ger, 2001):
R
SH
S
ðÞ¼
1
2
I
S
I
S
þ
1
2
V
S
V
S
tan
2
S
where y
S
is the SH-wave phase angle of incidence.
For P-to-SV converted shear-wave reflection (Aki and Richards, 1980):
R
PS
S
ðÞ
tan
S
2
V
S
=
V
P
1 2 sin
2
S
þ 2 cos
S
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
V
S
V
P
2
sin
2
S
s
0
@
1
A
þ
tan
S
2
V
S
=
V
P
4 sin
2
S
4 cos
S
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
V
S
V
P
2
sin
2
S
s
0
@
1
A
V
S
V
S
where y
S
is the S-wave phase angle of reflection. This can be rewritten as (Gonza
´
lez,
2006)
R
PS
ðÞ
sin
ð
V
P
=
V
S
Þ
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
V
P
=
V
S
ðÞ
2
sin
2
q
1
2
V
P
V
S
2
sin
2
þ cos
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
V
P
V
S
2
sin
2
s
2
4
3
5
8
<
:
2 sin
2
2 cos
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
V
P
V
S
2
sin
2
s
2
4
3
5
V
S
V
S
9
=
;
where y is the P-wave phase angle of incidence.
For small angles, Duffaut et al. (2000) give the following expression for R
PS
(y):
R
PS
ðÞ
1
2
1 þ 2
V
S
V
P
2
V
S
V
P
V
S
V
S
sin
þ
V
S
V
P
V
S
V
P
þ
1
2
þ
2V
S
V
S
1
4
V
S
V
P
sin
3
which can be simplified further (Jı
´
lek, 2002b)to
R
PS
ðÞ
1
2
1 þ 2
V
S
V
P
2
V
S
V
P
V
S
V
S
sin
104 Seismic wave propagation
Assumptions and limitations
The equations presented in this section apply in the following cases:
the rock is linear, isotropic, and elastic;
plane-wave propagation is assumed; and
most of the simplified forms assume small contrasts in material properties across the
boundary and angles of incidence of less than about 30
. The simplified form for
P-to-S reflection given by Gonza
´
lez (2006) is valid for large angles of incidence.
3.6 Plane-wave reflectivity in anisotropic media
Synopsis
An incident wave at a boundary between two anisotropic media (Figure 3.6.1) can
generate reflected quasi-P-waves and quasi-S-waves as well as transmitted quasi-
P-waves and quasi-S-waves (Auld, 1990). In general, the reflection and transmission
coefficients vary with offset and azimuth. The AVOA (amplitude variation with
offset and azimuth) can be detected by three-dimensional seismic surveys and is a
useful seismic attribute for reservoir characterization.
Brute-force modeling of AVOA by solving the Zoeppritz (1919) equations can be
complicated and unintuitive for several reasons: for anisotropic media in general, the
two shear waves are separate (shear-wave birefringence); the slowness surfaces are
nonspherical and are not necessarily convex; and the polarization vectors are neither
parallel nor perpendicular to the propagation vectors.
Schoenberg and Prota
´
zio (1992) give explicit solutions for the plane-wave reflec-
tion and transmission problem in terms of submatrices of the coefficient matrix of the
Zoeppritz equations. The most general case of the explicit solutions is applicable to
Incident qP-wave
Reflected
qP-wave
Reflected
qS-wave
Transmitted
qP-wave
Transmitted
qS-wave
q
1
q
2
r
1
, a
1
, b
1
, e
1
, d
1
, g
1
r
2
, a
2
, b
2
, e
2
, d
2
, g
2
Figure 3.6.1 Reflected and transmitted rays caused by a P-wave incident at a boundary between two
anisotropic media.
105 3.6 Plane-wave reflectivity in anisotropic media

monoclinic media with a mirror plane of symmetry parallel to the reflecting plane.
Let R and T represent the reflection and transmission matrices, respectively,
R ¼
R
PP
R
SP
R
TP
R
PS
R
SS
R
TS
R
PT
R
ST
R
TT
2
6
4
3
7
5
T ¼
T
PP
T
SP
T
TP
T
PS
T
SS
T
TS
T
PT
T
ST
T
TT
2
4
3
5
where the first subscript denotes the type of incident wave and the second subscript
denotes the type of reflected or transmitted wave. For “weakly” anisotropic media, the
subscript P denotes the P-wave, S denotes one quasi-S-wave, and T denotes the other
quasi-S-wave (i.e., the tertiary or third wave). As a convention for real s
2
3P
, s
2
3S
, and s
2
3T
,
s
2
3P
< s
2
3S
< s
2
3T
where s
3i
is the vertical component of the phase slowness of the ith wave type when
the reflecting plane is horizontal. An imaginary value for any of the vertical slow-
nesses implies that the corresponding wave is inhomogeneous or evanescent. The
impedance matrices are defined as
X ¼
e
P1
e
S1
e
T1
e
P2
e
S2
e
T2
fðC
13
e
P1
þ C
36
e
P2
Þs
1
ðC
23
e
P2
þ C
36
e
P1
Þs
2
C
33
e
P3
s
3P
g
fðC
13
e
S1
þ C
36
e
S2
Þs
1
ðC
23
e
S2
þ C
36
e
S1
Þs
2
C
33
e
S3
s
3S
g
fðC
13
e
T1
þ C
36
e
T2
Þs
1
ðC
23
e
T2
þ C
36
e
T1
Þs
2
C
33
e
T3
s
3T
g
2
6
6
6
6
6
4
3
7
7
7
7
7
5
Y ¼
fðC
55
s
1
þ C
45
s
2
Þe
P3
ðC
55
e
P1
þ C
45
e
P2
Þs
3P
g
fðC
55
s
1
þ C
45
s
2
Þe
S3
ðC
55
e
S1
þ C
45
e
S2
Þs
3S
g
fðC
55
s
1
þ C
45
s
2
Þe
T3
ðC
55
e
T1
þ C
45
e
T2
Þs
3T
g
fðC
45
s
1
þ C
44
s
2
Þe
P3
ðC
45
e
P1
þ C
44
e
P2
Þs
3P
g
fðC
45
s
1
þ C
44
s
2
Þe
S3
ðC
45
e
S1
þ C
44
e
S2
Þs
3S
g
fðC
45
s
1
þ C
44
s
2
Þe
T3
ðC
45
e
T1
þ C
44
e
T2
Þs
3T
g
e
P3
e
S3
e
T3
2
6
6
6
6
6
6
6
4
3
7
7
7
7
7
7
7
5
where s
1
and s
2
are the horizontal components of the phase slowness vector; e
P
, e
S
,
and e
T
are the associated eigenvectors evaluated from the Christoffel equations (see
Section 3.2), and C
IJ
denotes elements of the stiffness matrix of the incident medium.
X
0
and Y
0
are the same as above except that primed parameters (transmission
medium) replace unprimed parameters (incidence medium). When neither X nor Y
is singular and (X
–1
X
0
þ Y
–1
Y
0
) is invertible, the reflection and transmission coeffi-
cients can be written as
106 Seismic wave propagation
