Mavko G., Mukerji T., Dvorkin J. The Rock Physics Handbook
Подождите немного. Документ загружается.


T ¼2ðX
1
X
0
þ Y
1
Y
0
Þ
1
R ¼ðX
1
X
0
Y
1
Y
0
ÞðX
1
X
0
þ Y
1
Y
0
Þ
1
Schoenberg and Prota
´
zio (1992) point out that a singularity occurs at a horizontal
slowness for which an interface wave (e.g., a Stoneley wave) exists. When Y is
singular, straightforward matrix manipulations yield
T ¼2Y
01
YðX
1
X
0
Y
01
Y þ IÞ
1
R ¼ðX
1
X
0
Y
01
Y þ IÞ
1
ðX
1
X
0
Y
01
Y IÞ
Similarly, T and R can also be written without X
–1
when X is singular as
T ¼2X
01
XðI þ Y
1
Y
0
X
01
XÞ
1
R ¼ðI þ Y
1
Y
0
X
01
XÞ
1
ðI Y
1
Y
0
X
01
XÞ
Alternative solutions can be found by assuming that X
0
and Y
0
are invertible
R ¼ðY
01
Y þ X
01
XÞ
1
ðY
01
Y X
01
XÞ
T ¼2X
01
XðY
01
Y þ X
01
XÞ
1
Y
01
Y
¼2Y
01
YðY
01
Y þ X
01
XÞ
1
X
01
X
These formulas allow more straightforward calculations when the media have at
least monoclinic symmetry with a horizontal symmetry plane.
For a wave traveling in anisotropic media, there will generally be out-of-plane
motion unless the wave path is in a symmetry plane. These symmetry planes include
all vertical planes in VTI (transversely isotropic with vertical symmetry axis) media
and the symmetry planes in HTI (transversely isotropic with horizontal symmetry
axis) and orthorhombic media. In this case, the quasi-P- and the quasi-S-waves in the
symmetry plane uncouple from the quasi-S-wave polarized transversely to the
symmetry plane. For weakly anisotropic media, we can use simple analytical formulas
(Banik, 1987; Thomsen, 1993;Chen,1995;Ru
¨
ger, 1995, 1996)tocomputeAVOA
(amplitude variation with offset and azimuth) responses at the interface of anisotropic
media that can be either VTI, HTI, or orthorhombic. The analytical formulas give
more insight into the dependence of AVOA on anisotropy. Vavryc
ˇ
uk and Ps
ˇ
enc
ˇ
ı
´
k
(1998) and Ps
ˇ
enc
ˇ
ı
´
k and Martins (2001) provide formulas for arbitrary weak
anisotropy.
107 3.6 Plane-wave reflectivity in anisotropic media

Transversely isotropic media: VTI
Thomsen (1986) introduced the following notation for weakly anisotropic VTI media
with density r:
¼
ffiffiffiffiffiffiffi
C
33
s
; " ¼
C
11
C
33
2C
33
¼
ffiffiffiffiffiffiffi
C
44
s
; ¼
C
66
C
44
2C
44
¼
ðC
13
þ C
44
Þ
2
ðC
33
C
44
Þ
2
2C
33
ðC
33
C
44
Þ
In this chapter we use ¼
ffiffiffiffiffiffiffiffiffiffiffiffi
C
33
=
p
to refer to the P-wave velocity along the x
3
-
(vertical) axis in anisotropic media. We use b to refer to the S-wave velocity along the
x
3
-axis. The P-wave reflection coefficient for weakly anisotropic VTI media in the
limit of small impedance contrast was derived by Thomsen (1993) and corrected by
Ru
¨
ger (1997):
R
PP
ðÞ¼R
PP-iso
ðÞþR
PP-aniso
ðÞ
R
PP-iso
ðÞ
1
2
Z
Z
þ
1
2
2
2
"#
sin
2
þ
1
2
sin
2
tan
2
R
PP-aniso
ðÞ
2
sin
2
þ
"
2
sin
2
tan
2
where
¼
1
þ
2
ðÞ=2
¼
1
þ
2
ðÞ=2
¼
1
þ
2
ðÞ=2
¼
1
þ
2
ðÞ=2
Z ¼ Z
1
þ Z
2
ðÞ=2
Z
S
¼ Z
S1
þ Z
S2
ðÞ=2
¼
1
þ
2
ðÞ=2
" ¼ "
2
"
1
¼
2
1
¼
2
1
¼
2
1
Z ¼ Z
2
Z
1
Z
S
¼ Z
S2
Z
S1
¼
2
1
¼
2
1
¼
2
1
¼
2
Z ¼
Z
S
¼
In the preceding and following equations, D indicates a difference in properties
between layer 1 (above) and layer 2 (below) and an overbar indicates an average of
108 Seismic wave propagation
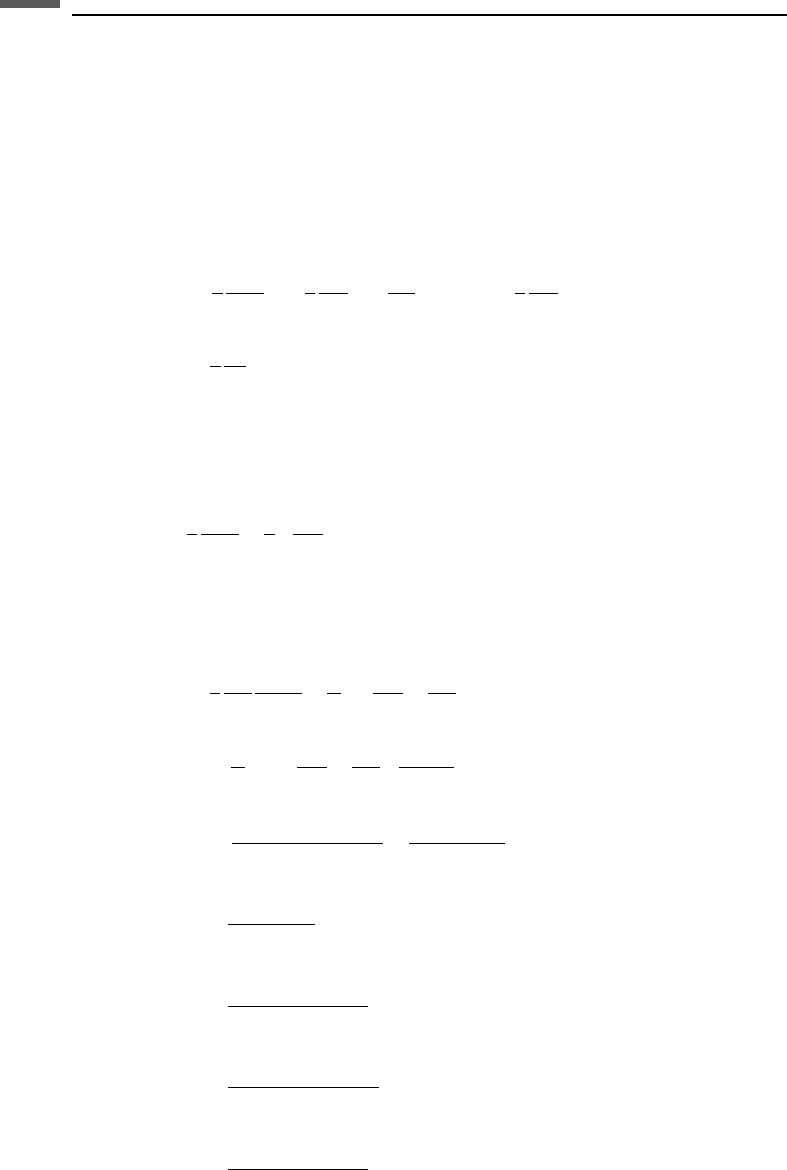
the corresponding quantities in the two layers. y is the P-wave phase angle of
incidence, Z ¼ is the vertical P-wave impedance, Z
S
¼ is the vertical S-wave
impedance, and ¼
2
is the vertical shear modulus. Note that the VTI anisotropy
causes perturbations of both the AVO gradient and far-offset terms.
Ru
¨
ger (2001) derived the corresponding SV-to-SV reflectivity in VTI media, again
under the assumption of weak anisotropy and small-layer contrast:
R
SV
S
ðÞ¼R
SV-iso
S
ðÞþR
SV-aniso
S
ðÞ
R
SV-iso
S
ðÞ
1
2
Z
S
Z
S
þ
7
2
þ 2
sin
2
S
1
2
tan
2
S
sin
2
S
R
SV-aniso
S
ðÞ¼
1
2
2
2
" ðÞsin
2
S
In the S-wave reflectivity equations, note that y
S
is the S-wave angle of incidence and
Z
S
¼ is the shear impedance. The weak anisotropy, weak contrast SH-to-SH
reflectivity is (Ru
¨
ger, 2001)
R
SH
S
ðÞ¼
1
2
Z
S
Z
S
þ
1
2
þ
tan
2
S
The P–S converted wave reflectivity in VTI media is given by (Ru
¨
ger, 2001)
R
PS
S
ðÞ¼R
PS-iso
S
ðÞþR
PS-aniso
S
ðÞ
R
PS-iso
S
ðÞ
1
2
sin
P
sin
S
2
þ
sin
P
cos
P
þ
2
2
þ
sin
3
P
cos
S
R
PS-aniso
S
ðÞ¼
2
2
2
2
cos
S
cos
P
2
2
2
!
2
1
ðÞ
"#
sin
P
þ
cos
P
2
2
2
1
þ "
1
"
2
ðÞ
"#
sin
3
P
2
2
2
cos
S
2
1
þ "
1
"
2
ðÞ
"#
sin
3
P
þ
2
2
2
2
cos
S
1
2
ðÞ
"#
sin
3
P
þ
2
2
2
cos
S
2
1
þ "
1
"
2
ðÞ
"#
sin
5
P
109 3.6 Plane-wave reflectivity in anisotropic media
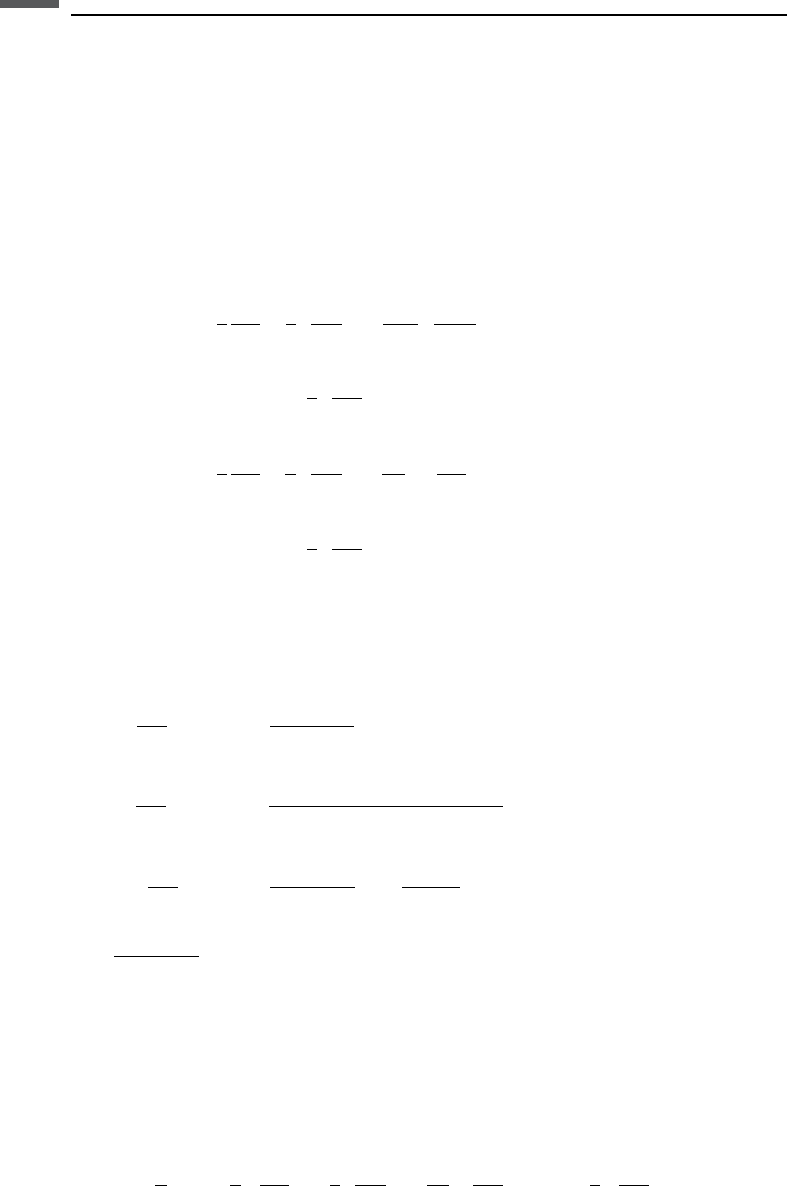
Transversely isotropic media: HTI
In HTI (transversely isotropic with horizontal symmetry axis) media, reflectivity will
vary with azimuth, z, as well as offset or incident angle y. Ru
¨
ger (1995, 1996) and
Chen (1995) derived the P-wave reflection coefficient in the symmetry planes for
reflections at the boundary of two HTI media sharing the same symmetry axis. At a
horizontal interface between two HTI media with horizontal symmetry axis x
1
and
vertical axis x
3
, the P-wave reflectivity for propagation in the vertical symmetry axis
plane (x
1
–x
3
plane) parallel to the x
1
symmetry axis can be written as
R
PP
¼ 0;ðÞ
1
2
Z
Z
þ
1
2
2
?
2
?
?
þ
VðÞ
"#
sin
2
þ
1
2
þ "
VðÞ
sin
2
tan
2
1
2
Z
Z
þ
1
2
2
2
2
þ
VðÞ
"#
sin
2
þ
1
2
þ "
VðÞ
sin
2
tan
2
where the azimuth angle z is measured from the x
1
-axis and the incident angle y is
defined with respect to x
3
. The isotropic part R
PP-iso
(y) is the same as before. In the
preceding expression
¼
ffiffiffiffiffiffiffi
C
33
s
; "
VðÞ
¼
C
11
C
33
2C
33
¼
ffiffiffiffiffiffiffi
C
44
s
;
VðÞ
¼
C
13
þ C
55
ðÞ
2
C
33
C
55
ðÞ
2
2C
33
C
33
C
55
ðÞ
?
¼
ffiffiffiffiffiffiffi
C
55
s
;
VðÞ
¼
C
66
C
44
2C
44
¼
1 þ 2
¼
C
44
C
66
2C
66
where b is the velocity of a vertically propagating shear wave polarized in the
x
2
direction and
?
is the velocity of a vertically propagating shear wave polarized
in the x
1
direction. ¼ c
44
and
?
¼ c
55
are the shear moduli corresponding to the
shear velocities b and
?
. In the vertical symmetry plane (x
2
–x
3
plane), perpendicular
to the symmetry axis, the P-wave reflectivity resembles the isotropic solution:
R
PP
¼
2
;
1
2
Z
Z
þ
1
2
2
2
"#
sin
2
þ
1
2
sin
2
tan
2
110 Seismic wave propagation

In nonsymmetry planes, Ru
¨
ger (1996) derived the P-wave reflectivity R
PP
;
ðÞ
using
a perturbation technique as follows:
R
PP
;
ðÞ
1
2
Z
Z
þ
1
2
2
2
þ
VðÞ
þ 2
2
2
!
cos
2
"#
sin
2
þ
1
2
þ "
VðÞ
cos
4
þ
VðÞ
sin
2
cos
2
sin
2
tan
2
where z is the azimuth relative to the x
1
-axis.
The reflectivity for SV- and SH-waves in the symmetry axis plane (x
1
–x
3
plane) of
the HTI medium is given by (Ru
¨
ger, 2001)
R
SV
S
ðÞR
SV-iso
S
ðÞþ
1
2
?
2
"
VðÞ
VðÞ
sin
2
S
R
SH
S
ðÞR
SH-iso
S
ðÞþ
1
2
VðÞ
tan
2
S
where
R
SV-iso
S
ðÞ
1
2
Z
?
S
Z
?
S
þ
7
2
?
?
þ 2
sin
2
S
1
2
?
?
tan
2
S
sin
2
S
R
SH-iso
S
ðÞ¼
1
2
Z
S
Z
S
þ
1
2
tan
2
S
For waves propagating in the (x
2
–x
3
) plane
R
SV
S
ðÞ
1
2
Z
S
Z
S
þ
7
2
þ 2
sin
2
S
1
2
tan
2
S
sin
2
S
R
SH
S
ðÞ¼
1
2
Z
?
S
Z
?
S
þ
1
2
?
?
tan
2
S
Orthorhombic media
The anisotropic parameters in orthorhombic media are given by Chen (1995) and
Tsvankin (1997) as follows:
¼
ffiffiffiffiffiffiffi
C
33
s
; ¼
ffiffiffiffiffiffiffi
C
44
s
;
?
¼
ffiffiffiffiffiffiffi
C
55
s
"
1ðÞ
¼
C
22
C
33
2C
33
; "
2ðÞ
¼
C
11
C
33
2C
33
1ðÞ
¼
C
23
þ C
44
ðÞ
2
C
33
C
44
ðÞ
2
2C
33
C
33
C
44
ðÞ
111 3.6 Plane-wave reflectivity in anisotropic media
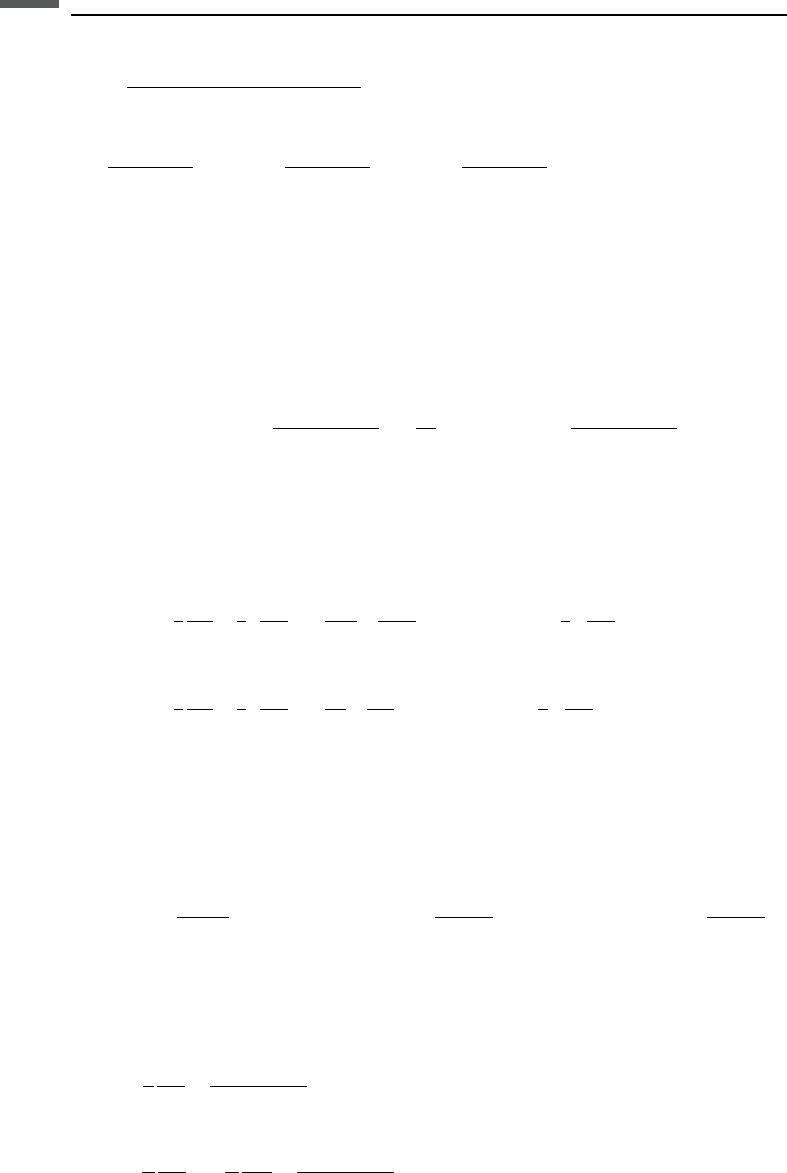
2ðÞ
¼
C
13
þ C
55
ðÞ
2
C
33
C
55
ðÞ
2
2C
33
C
33
C
55
ðÞ
¼
C
44
C
55
2C
55
;
1ðÞ
¼
C
66
C
55
2C
55
;
2ðÞ
¼
C
66
C
44
2C
44
The parameters e
(1)
and d
(1)
are Thomsen’s parameters for the equivalent TIV media in
the x
2
–x
3
plane. Similarly, e
(2)
and d
(2)
are Thomsen’s parameters for the equivalent
TIV media in the x
1
–x
3
plane; g
2
represents the velocity anisotropy between two shear-
wave modes traveling along the z-axis. The difference in the approximate P-wave
reflection coefficient in the two vertical symmetry planes (with x
3
as the vertical axis)
of orthorhombic media is given by Ru
¨
ger (1995, 1996) in the following form:
R
x
1
;x
3
ðÞ
PP
ðÞR
x
2
;x
3
ðÞ
PP
ðÞ
2ðÞ
1ðÞ
2
þ
2
2
"#
sin
2
þ
"
2ðÞ
"
1ðÞ
2
sin
2
tan
2
The equations are good approximations for angles of incidence of up to 30
–40
.
Ru
¨
ger (2001) gives the following expressions for P-wave reflectivity in the ortho-
rhombic symmetry planes:
R
x
1
;x
3
ðÞ
PP
ðÞ
1
2
Z
Z
þ
1
2
2
?
2
?
?
þ
ð2Þ
"#
sin
2
þ
1
2
þ "
ð2Þ
sin
2
tan
2
R
x
2
;x
3
ðÞ
PP
ðÞ
1
2
Z
Z
þ
1
2
2
2
þ
ð1Þ
"#
sin
2
þ
1
2
þ "
ð1Þ
sin
2
tan
2
Jı
´
lek (2002a, b) derived expressions for P-to-SV reflectivity for arbitrary weak
anisotropy and weak layer contrasts. In the case of orthorhombic and higher symmet-
ries with aligned vertical symmetry planes, the expressions for P–SV in the vertical
symmetry planes simplify to
R
PSV
¼B
1
sin
P
cos
S
þ B
2
cos
P
sin
P
þ B
3
sin
3
P
cos
S
þ B
4
cos
P
sin
3
P
þ B
5
sin
5
P
cos
S
where
P
is the P-wave incident phase angle and
S
is the converted S-wave
reflection phase angle.
In the x–z symmetry plane (the z-axis is vertical), the coefficients B
i
are
B
1
¼
1
2
þ
2
2
2
2
~
2ðÞ
2
~
2ðÞ
1
B
2
¼
2
2
2
2
~
2ðÞ
2
~
2ðÞ
1
112 Seismic wave propagation

B
3
¼
2
2
þ 2
2
2
þ
2
2
2
2
~
2ðÞ
1
~
2ðÞ
2
þ
2
2
2
"
2ðÞ
2
"
2ðÞ
1
þ
~
2ðÞ
1
~
2ðÞ
2
hi
B
4
¼
2
2
"
2ðÞ
2
"
2ðÞ
1
þ
~
2ðÞ
1
~
2ðÞ
2
hi
B
5
¼
2
2
2
"
2ðÞ
2
"
2ðÞ
1
þ
~
2ðÞ
1
~
2ðÞ
2
hi
and in the y–z symmetry plane, the coefficients are
B
1
¼
1
2
þ
2
2
2
2
~
1ðÞ
2
~
1ðÞ
1
B
2
¼
2
2
2
2
~
1ðÞ
2
~
1ðÞ
1
2
SðÞ
2
SðÞ
1
B
3
¼
2
2
þ 2
2
2
þ
2
2
2
2
~
1ðÞ
1
~
1ðÞ
2
þ
2
2
2
"
1ðÞ
2
"
1ðÞ
1
þ
~
1ðÞ
1
~
1ðÞ
2
þ 2
2
2
SðÞ
2
SðÞ
1
B
4
¼
2
2
"
1ðÞ
2
"
1ðÞ
1
þ
~
1ðÞ
1
~
1ðÞ
2
B
5
¼
2
2
2
"
1ðÞ
2
"
1ðÞ
1
þ
~
1ðÞ
1
~
1ðÞ
2
In these expressions, a subscript 1 on "
mðÞ
1
,
~
mðÞ
1
, and
SðÞ
1
refers to properties of the
incident layer and a subscript 2 on "
mðÞ
2
,
~
mðÞ
2
, and
SðÞ
2
refers to properties of the
reflecting layer. “Background” isotropic P- and S-wave velocities are defined within
each layer (I = 1, 2 refer to the incident and reflecting layers, respectively) and can be
taken to be equal to the actual vertical velocities within those layers:
I
¼
ffiffiffiffiffiffiffiffi
A
IðÞ
33
q
;
I
¼
ffiffiffiffiffiffiffiffi
A
IðÞ
55
q
In addition, the overall isotropic “background” P-wave velocity, S-wave velocity, and
density are defined as averages over the two layers:
¼
1
2
1
þ
2
ðÞ;
¼
1
2
1
þ
2
ðÞ;
¼
1
2
1
þ
2
ðÞ
113 3.6 Plane-wave reflectivity in anisotropic media

and contrasts across the boundary are defined as
¼
2
1
; ¼
2
1
; ¼
2
1
The anisotropic parameters of each layer are defined as
"
1ðÞ
I
¼
A
IðÞ
22
A
IðÞ
33
2A
IðÞ
33
;
"
2ðÞ
I
¼
A
IðÞ
11
A
IðÞ
33
2A
IðÞ
33
;
SðÞ
I
¼
A
IðÞ
44
A
IðÞ
55
2A
IðÞ
55
;
~
1ðÞ
I
¼
A
IðÞ
23
þ 2A
IðÞ
44
A
IðÞ
33
A
IðÞ
33
~
2ðÞ
I
¼
A
IðÞ
13
þ 2A
IðÞ
55
A
IðÞ
33
A
I
ðÞ
33
~
3ðÞ
I
¼
A
IðÞ
12
þ 2A
IðÞ
66
A
IðÞ
11
A
IðÞ
11
where A
IðÞ
jk
are the density-normalized Voigt-notation elastic constants of each layer.
In the approximation of weak anisotropy and weak layer contrasts,
S
can be
related approximately to
P
using the linearized isotropic Snell’s law:
1
cos
S
1
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 ð
2
=
2
Þsin
2
P
q
1 þ
1
2
2
2
sin
2
P
Arbitrary anisotropy
Vavryc
ˇ
uk and Ps
ˇ
enc
ˇ
ik (1998) derived P-wave reflectivity for arbitrary weak aniso-
tropy and weak layer contrast:
R
PP
;
P
ðÞ¼
1
2
Z
Z
þ
1
2
4
2
"#
sin
2
P
þ
1
2
tan
2
P
sin
2
P
þ
1
2
A
13
þ 2A
55
A
33
A
33
cos
2
þ
A
23
þ 2A
44
A
33
A
33
8
A
44
A
55
2A
33
sin
2
þ 2
A
36
þ 2A
45
A
33
4
A
45
A
33
cos sin
sin
2
P
þ
1
2
A
11
A
33
2A
33
cos
4
þ
A
22
A
33
2A
33
sin
4
þ
A
12
þ 2A
66
A
33
A
33
cos
2
sin
2
þ 2
A
16
A
33
cos
3
sin
þ2
A
26
A
33
cos sin
3
sin
2
P
tan
2
P
114 Seismic wave propagation

where A
ij
¼ c
ij
= is the Voigt-notation elastic constant divided by density.
P
is the
P-wave angle of incidence and z is the azimuth relative to the x
1
-axis. D signifies
the contrast of any parameter across the reflector, e.g., ¼
2
1
.
,
, and r are
the background average isotropic P-wave velocity, S-wave velocity, and density,
respectively. The accuracy of the result varies slightly with the choice of the
background values, but a reasonable choice is the average of the vertical P-wave
velocities across the two layers for
, the average of the vertical S-wave velocities
across the reflector for
, and the average of the densities across the two layers for r.
The corresponding expression for the P-wave transmission coefficient for arbitrary
anisotropy is given by Ps
ˇ
enc
ˇ
ik and Vavryc
ˇ
uk (1998).
Jı
´
lek (2002a, b) derived expressions for P-to-SV reflectivities for arbitrary weak
anisotropy and weak layer contrasts.
Assumptions and limitations
The equations presented in this section apply under the following conditions:
the rock is linear elastic;
approximate forms apply to the P–P reflection at near offset for slightly contrasting,
weakly anisotropic media.
3.7 Elastic impedance
The elastic impedance is a pseudo-impedance attribute (Connolly, 1998; Mukerji
et al., 1998) and is a far-offset equivalent of the more conventional zero-offset
acoustic impedance. This far-offset impedance has been called the “elastic imped-
ance” (EI), as it contains information about the V
P
=V
S
ratio. One can obtain the elastic
impedance cube from a far-offset stack using the same trace-based one-dimensional
inversion algorithm used to invert the near-offset stack. Though only approximate,
the inversion for elastic impedance is economical and simple compared to full prestack
inversion. As with any impedance inversion, the key to effectively using this extracted
attribute for quantitative reservoir characterization is calibration with log data.
The acoustic impedance, I
a
¼ V
P
, can be expressed as
I
a
¼ exp 2
Z
R
PP
ð0Þdt
where R
PP
0ðÞis the time sequence of normal-incidence P-to-P reflection coefficients.
Similarly, the elastic impedance may be defined in terms of the sequence of non-
normal P–P reflection coefficients, R
PP
ðÞ, at incidence angle y as
I
e
ðÞ¼exp 2
Z
R
PP
ðyÞdt
115 3.7 Elastic impedance

Substituting into this equation one of the well-known approximations for R
PP
ðÞ
(e.g.,
Aki and Richards, 1980),
R
PP
ðÞR
PP
ð0ÞþM sin
2
þ N tan
2
R
PP
ð0Þ¼
1
2
V
P
V
P
þ
M ¼2
V
S
V
P
2
2V
S
V
S
þ
N ¼
1
2
V
P
V
P
leads to the following expression for I
e
:
I
e
ðÞ¼V
P
exp
tan
2
Z
dðln V
P
Þ
exp
4 sin
2
V
S
=
V
P
ðÞ
2
Z
2dðln V
S
Þ
exp 4 sin
2
V
S
=
V
P
ðÞ
2
Z
dðln Þ
or
I
e
ðÞ¼V
ð1þtan
2
Þ
P
ð14K sin
2
Þ
V
ð8K sin
2
Þ
S
where K ¼
V
S
=
V
P
ðÞ
2
is taken to be a constant. The elastic impedance reduces to
the usual acoustic impedance, I
a
¼ V
P
,wheny ¼ 0. Unlike the acoustic imped-
ance, the elastic impedance is not a function of the rock properties alone but also
depends on the angle of incidence. Using only the first two terms i n the approxi-
mation for R ðÞgives a similar expression for I
e
with the tan
2
terms being
replaced by sin
2
;
I
e
ðÞ¼V
ð1þsin
2
Þ
P
ð14K sin
2
Þ
V
ð8K sin
2
Þ
S
This last expression has been referred to as the first-order elastic impedance
(Connolly, 1999), and it goes to V
P
=V
S
ðÞ
2
at ¼ 90
, assuming K ¼
1
4
. Expressions
for P-to-S converted-wave elastic impedance have been given by Duffaut et al.
(2000) and Gonza
´
lez (2006). The elastic impedance has strange units and dimensions
116 Seismic wave propagation
