Mavko G., Mukerji T., Dvorkin J. The Rock Physics Handbook
Подождите немного. Документ загружается.


that change with angle. Whitcombe (2002) defines a useful normalization for the
elastic impedance:
I
e
ðÞ¼½V
P0
0
V
P
V
P0
ð1þtan
2
Þ
0
ð14K sin
2
Þ
V
S
V
S0
ð8K sin
2
Þ
where the normalizing constants V
P0
, V
S0
,andr
0
may be taken to be either the
average values of velocities and densities over the zone of interest, or the values at
the top of the target zone. With this normalization, the elastic impedance has the
same dimensionality as the acoustic impedance. The extended elastic impedance
(EEI) (Whitcombe et al., 2002) is defined over an a ngle w, ranging from –90
to
þ90
. The angle w should not be interpreted as the actual reflection angle, but
rather as the independent input variable in the definition of EEI. The EEI is
expressed as
I
e
ðÞ¼½V
P0
0
V
P
V
P0
ðcos þsin Þ
0
ðcos 4K sin Þ
V
S
V
S0
ð8K sin Þ
Under certain approximations, the EEI for specific values of w becomes
proportional to rock elastic parameters such as the bulk modulus and the shear
modulus.
In applications to reservoir characterization, care must be taken to filter the logs to
match the seismic frequencies, as well as to account for the differences in frequency
content in near- and far-offset data. Separate wavelets should be extracted for the
near- and far-offset angle stacks. The inverted acoustic and elastic impedances
co-located at the wells must be calibrated with the known facies and fluid types in
the well, before classifying the seismic cube in the interwell region.
Major limitations in using partial-stack elastic-impedance inversion arise from the
assumptions of the one-dimensional convolutional model for far offsets, the assump-
tion of a constant value for K, and errors in estimates of the incidence angle. The
convolutional model does not properly handle all the reflections at far offsets,
because the primary reflections get mixed with other events. The approximations
used to derive the expressions for elastic impedance become less accurate at larger
angles. The first-order, two-term elastic impedance has been found to give stabler
results than the three-term elastic impedance (Mallick, 2001). Mallick compares
prestack inversion versus partial-stack elastic impedance inversions and recommends
a hybrid approach. In this approach, full prestack inversion is done at a few control
points to get reliable estimates of P and S impedance. These prestack inversions are
used as anchors for cheaper, one-dimensional, trace-based inversions over large data
volumes. Based on these results, small zones may be selected for detailed analysis by
prestack inversions.
117 3.7 Elastic impedance

Elastic impedance expressions: isotropic
Table 3.7.1 Exponents in expressions for elastic impedance of an isotropic, flat-layered
Earth, EI V
A
P
V
B
S
C
. In all expressions, y is the P-wave angle of incidence and y
S
is
the shear-wave angle of incidence. Expressions are given for P–P reflection,
converted wave reflections P–S and S–P, and shear-wave reflections SV–SV and SH–SH.
V
2
S
=
V
2
P
and
V
S
=
V
P
hi
are assumed to be constant, often taken as the average of the
corresponding quantities.
P–P A 1 þ tan
2
B 8
V
2
S
V
2
P
sin
2
C1 4
V
2
S
V
2
P
sin
2
P–SV A 0
B
sin
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
V
2
S
=
V
2
P
sin
2
q
4 sin
2
V
2
S
V
2
P
4
V
S
V
P
cos
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
V
2
S
V
2
P
sin
2
s
!
C
sin
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
V
2
S
=
V
2
P
sin
2
q
1 2
V
2
S
V
2
P
sin
2
þ 2
V
S
V
P
cos
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
V
2
S
V
2
P
sin
2
s
!
SV–P A 0
B
sin
S
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
V
2
S
=
V
2
P
1
sin
2
S
q
4 sin
2
S
4
V
S
V
P
cos
S
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
V
2
S
V
2
P
1
sin
2
S
s
0
@
1
A
C
sin
S
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
V
2
S
=
V
2
P
1
sin
2
S
q
1 2 sin
2
S
þ 2
V
S
V
P
cos
S
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
V
2
S
V
2
P
1
sin
2
S
s
0
@
1
A
SV–SV A 0
B
1
cos
2
S
þ 8 sin
2
S
C 1 þ 4 sin
2
S
SH–SH A 0
B 1 þ tan
2
S
C 1
118 Seismic wave propagation

Elastic impedance expressions: VTI anisotropic
Table 3.7.2 Exponents in expressions for elastic impedance of a VTI, flat-layered
Earth, EI V
A
P
V
B
S
C
exp D" þ E þ F
ðVÞ
. y is the P-wave angle of incidence,
and y
S
is the shear-wave angle of incidence. Expressions are given for P–P
reflection, and shear-wave reflections SV–SV and SH–SH.
V
2
S
=
V
2
P
is assumed to
be constant, often taken as the average of the squared velocity ratio.
P–P A
1 þ tan
2
B
8
V
2
S
V
2
P
sin
2
C
1 4
V
2
S
V
2
P
sin
2
D
sin
2
tan
2
E
sin
2
F0
SV–SV A 0
B
1
cos
2
S
þ 8 sin
2
S
C
1 þ4 sin
2
S
D
sin
2
S
=
V
2
S
V
2
P
E
sin
2
S
=
V
2
S
V
2
P
F0
SH–SH A 0
B
1 þtan
2
S
C
1
D0
E0
F
tan
2
S
119 3.7 Elastic impedance

V
P
¼ ¼
ffiffiffiffiffiffiffiffiffiffiffi
c
33
=
p
; V
S
¼ ¼
ffiffiffiffiffiffiffiffiffiffiffi
c
44
=
p
" ¼
c
11
c
33
2c
33
;
ðVÞ
¼
c
66
c
44
2c
44
; ¼
c
13
þ c
44
ðÞ
2
c
33
c
44
ðÞ
2
2c
33
c
33
c
44
ðÞ
Elastic impedance expressions: orthorhombic x
1
–x
3
symmetry plane
Elastic impedance expressions: orthorhombic x
2
–x
3
symmetry plane
Table 3.7.3 Exponents in expressions for P–P elastic impedance of an
orthorhombic, flat-layered Earth, EI V
A
P
V
?B
S
C
exp D"
2ðÞ
þ E
2ðÞ
. y is the
P-wave angle of incidence.
V
2
S
=
V
2
P
is assumed to be constant, often taken as
the average of the squared velocity ratio. V
P
¼
ffiffiffiffiffiffiffiffiffiffiffi
c
33
=
p
; V
?
S
¼
?
¼
ffiffiffiffiffiffiffiffiffiffiffi
c
55
=
p
P–P A
1 þ tan
2
B
8
V
?2
S
V
2
P
sin
2
C
1 4
V
?2
S
V
2
P
sin
2
D
sin
2
tan
2
E
sin
2
Table 3.7.4 Exponents in expressions for P–P elastic impedance of an
orthorhombic, flat-layered Earth, EI V
A
P
V
B
S
C
exp D"
1ðÞ
þ E
1ðÞ
. y is the
P-wave angle of incidence.
V
?2
S
=
V
2
P
is assumed to be constant, often taken as
the average of the squared velocity ratio. V
P
¼
ffiffiffiffiffiffiffiffiffiffiffi
c
33
=
p
; V
S
¼ ¼
ffiffiffiffiffiffiffiffiffiffiffi
c
44
=
p
P–P A
1 þ tan
2
B
8
V
2
S
V
2
P
sin
2
C
1 4
V
2
S
V
2
P
sin
2
D
sin
2
tan
2
E
sin
2
120 Seismic wave propagation

"
2ðÞ
¼
c
11
c
33
2c
33
;
2ðÞ
¼
c
13
þ c
55
ðÞ
2
c
33
c
55
ðÞ
2
2c
33
c
33
c
55
ðÞ
;
2ðÞ
¼
c
66
c
44
2c
44
;
"
1ðÞ
¼
c
22
c
33
2c
33
1ðÞ
¼
c
23
þ c
44
ðÞ
2
c
33
c
44
ðÞ
2
2c
33
c
33
c
44
ðÞ
1ðÞ
¼
c
66
c
55
2c
55
3ðÞ
¼
c
12
þ c
66
ðÞ
2
c
11
c
66
ðÞ
2
2c
11
c
11
c
66
ðÞ
Uses
The elastic impedance provides an alternative for interpreting far-offset data. As with
any inversion, the elastic impedance removes some wavelet effects and attempts to
determine interval properties from the band-limited reflectivity (seismic traces).
Assumptions and limitations
Limitations of using partial-stack elastic impedance inversion arise from the
assumptions of the one-dimensional convolutional model for far offsets, the
assumption of a c onstant value for K ¼ðV
S
=V
P
Þ
2
, and erro rs in estimates of
the incidence angle. The convolutional model does not properly handle all the
reflections at far offsets because the primary r eflections get mixed with other
events. Furthermore, approximations used to derive the expressions for elastic
impedance get worse at larger angles. The first-order two-term elastic impedance
has been found to give more stable results than the three-term elastic impedance
(Mallick, 2001).
3.8 Viscoelasticity and Q
Synopsis
Materials are linear elastic when the stress is proportional to the strain:
11
þ
22
þ
33
3
¼Kð"
11
þ "
22
þ "
33
Þ volumetric
ij
¼2"
ij
; i 6¼ j shear
ij
¼l
ij
"
kk
þ 2"
ij
general isotropic
where s
ij
and e
ij
are the stress and strain, K is the bulk modulus, m is the shear
modulus, and l is Lame
´
’s coefficient.
121 3.8 Viscoelasticity and Q
In contrast, linear, viscoelastic materials also depend on rate or history, which can
be incorporated by using time derivatives. For example, shear stress and shear strain
may be related by using one of the following simple models:
_
"
ij
¼
_
ij
2
þ
ij
2
Maxwell solid ð3:8:1Þ
ij
¼ 2
_
"
ij
þ 2"
ij
Voigt solid ð3:8:2Þ
_
ij
þðE
1
þ E
2
Þ
ij
¼ E
2
ð
_
"
ij
þ E
1
"
ij
Þ standardlinearsolid ð3:8:3Þ
where E
1
and E
2
are additional elastic moduli and is a material constant resembling
viscosity.
More generally, one can incorporate higher-order derivatives, as follows:
X
N
i¼0
a
i
@
i
"
@t
i
¼
X
M
j¼0
b
j
@
j
@t
j
Similar equations would be necessary to describe the generalizations of other elastic
constants such as K.
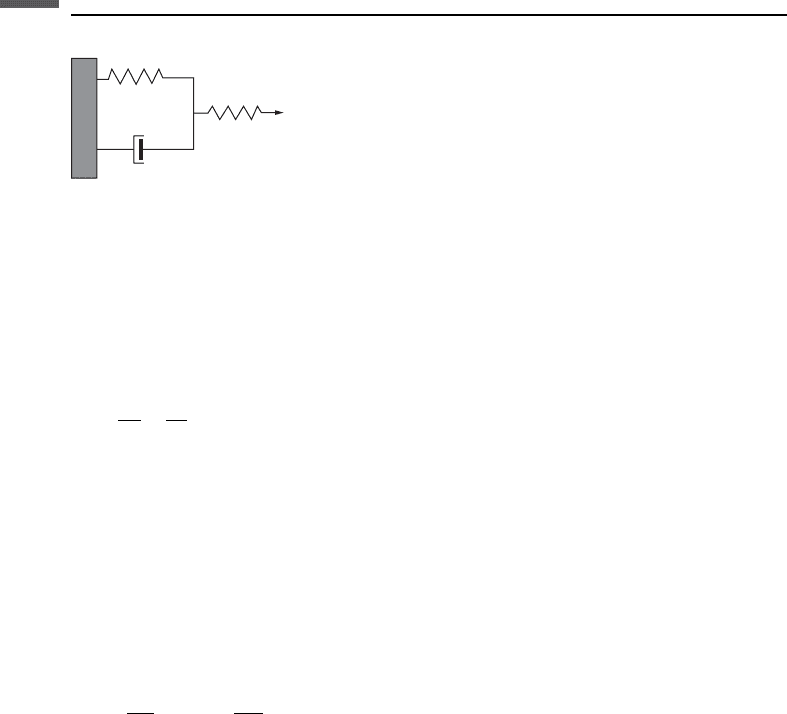
It is customary to represent these equations with mechanical spring and dashpot
models such as that for the standard linear solid shown in Figure 3.8.1.
Consider a wave propagating in a viscoelastic solid so that the displacement, for
example, is given by
uðx; tÞ¼u
0
exp½ðoÞxexp½iðot kxÞ ð3:8:4Þ
Then at any point in the solid the stress and strain are out of phase
¼
0
exp½iðot kxÞ ð3:8:5Þ
" ¼ "
0
exp½iðot kx ’Þ ð3:8:6Þ
The ratio of stress to strain at the point is the complex modulus, M(o).
h
E
1
E
2
Figure 3.8.1 Schematic of a spring and dashpot system for which the force – displacement
relation is described by the same equation as the standard linear solid.
122 Seismic wave propagation

The quality factor, Q, is a measure of how dissipative the material is. The lower Q,
the larger the dissipation is. There are several ways to express Q. One precise way is
as the ratio of the imaginary and real parts of the complex modulus:
1
Q
¼
M
I
M
R
In terms of energies, Q can be expressed as
1
Q
¼
W
2W
where DW is the energy dissipated per cycle of oscillation and W is the peak strain
energy during the cycle. In terms of the spatial attenuation factor, a,inequation (3.8.4),
1
Q
V
f
where V is the velocity and f is the frequency. In terms of the wave amplitudes of an
oscillatory signal with period t,
1
Q
1
ln
uðtÞ
uðt þ tÞ
which measures the amplitude loss per cycle. This is sometimes called the logarith-
mic decrement. Finally, in terms of the phase delay ’ between the stress and strain,
as in equations (3.8.5) and (3.8.6)
1
Q
tanð’Þ
Winkler and Nur (1979) showed that if we define Q
E
¼ E
R
/E
I
, Q
K
¼ K
R
/K
I
, and
Q
m
¼ m
R
/m
I
, where the subscripts R and I denote real and imaginary parts of the
Young, bulk, and shear moduli, respectively, and if the attenuation is small, then the
various Q factors can be related through the following equations:
ð1 vÞð1 2vÞ
Q
P
¼
ð1 þ vÞ
Q
E
2vð2 vÞ
Q
S
;
Q
P
Q
S
¼
I
K
I
þ
4
3
I
V
2
P
V
2
S
ð1 þ vÞ
Q
K
¼
3ð1 vÞ
Q
P
2ð1 2vÞ
Q
S
;
3
Q
E
¼
ð1 2vÞ
Q
K
þ
2ð1 þ vÞ
Q
S
One of the following relations always occurs (Bourbie
´
et al., 1987):
Q
K
> Q
P
> Q
E
> Q
S
for high V
P
=V
S
ratios
Q
K
< Q
P
< Q
E
< Q
S
for low V
P
=V
S
ratios
Q
K
¼ Q
P
¼ Q
E
¼ Q
S
123 3.8 Viscoelasticity and Q

The spectral ratio method is a popular way to estimate Q in both the laboratory
and the field. Because 1/Q is a measure of the fractional loss of energy per cycle of
oscillation, after a fixed distance of propagation there is a tendency for shorter
wavelengths to be attenuated more than longer wavelengths. If the amplitude of the
propagating wave is
uðx; tÞ¼u
0
exp½ðoÞx¼u
0
exp
f
VQ
x
we can compare the spectral amplitudes at two different distances and determine Q
from the slope of the logarithmic decrement (Figure 3.8.2):
ln
Sðf ; x
2
Þ
Sðf ; x
1
Þ
¼
f
QV
ðx
2
x
1
Þ
A useful illustrative example is the standard linear solid (Zener, 1948)inequa-
tion (3.8.3). If we assume sinusoidal motion
" ¼ "
0
e
iot
¼
0
e
iot
and substitute into equation (3.8.3), we can write
0
¼ MðoÞ"
0
with the complex frequency-dependent modulus
MðoÞ¼
E
2
ðE
1
þ ioÞ
E
1
þ E
2
þ io
In the limits of low frequency and high frequency, we obtain the limiting moduli
M
0
¼
E
2
E
1
E
1
þ E
2
; o ! 0
M
1
¼ E
2
; o !1
Spectra (dB)
Frequency
ln S(x
1
)/S(x
2
)
S(x
2
)
S(x
1
)
Figure 3.8.2 The slope of the log of the spectral ratio (difference of the spectra in dB)
can be interpreted in terms of Q .
124 Seismic wave propagation

Note that at very low frequencies and very high frequencies the moduli are real and
independent of frequency, and thus in these limits the material behaves elastically. It is
useful to rewrite the frequency-dependent complex modulus in terms of these limits:
MðoÞ¼
M
1
h
M
0
þ i
o
o
r
ðM
1
M
0
Þ
1=2
i
M
1
þ i
o
o
r
ðM
1
M
0
Þ
1=2
and
Re½MðoÞ ¼
M
0
M
1
1 þ o=o
r
ðÞ
2
hi
M
1
þ o=o
r
ðÞ
2
M
0
Im½Mðo Þ ¼
ðo=o
r
Þ
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
M
0
M
1
p
ðM
1
M
0
Þ
M
1
þ o=o
r
ðÞ
2
M
0
where
o
r
¼
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
E
1
ðE
1
þ E
2
Þ
p
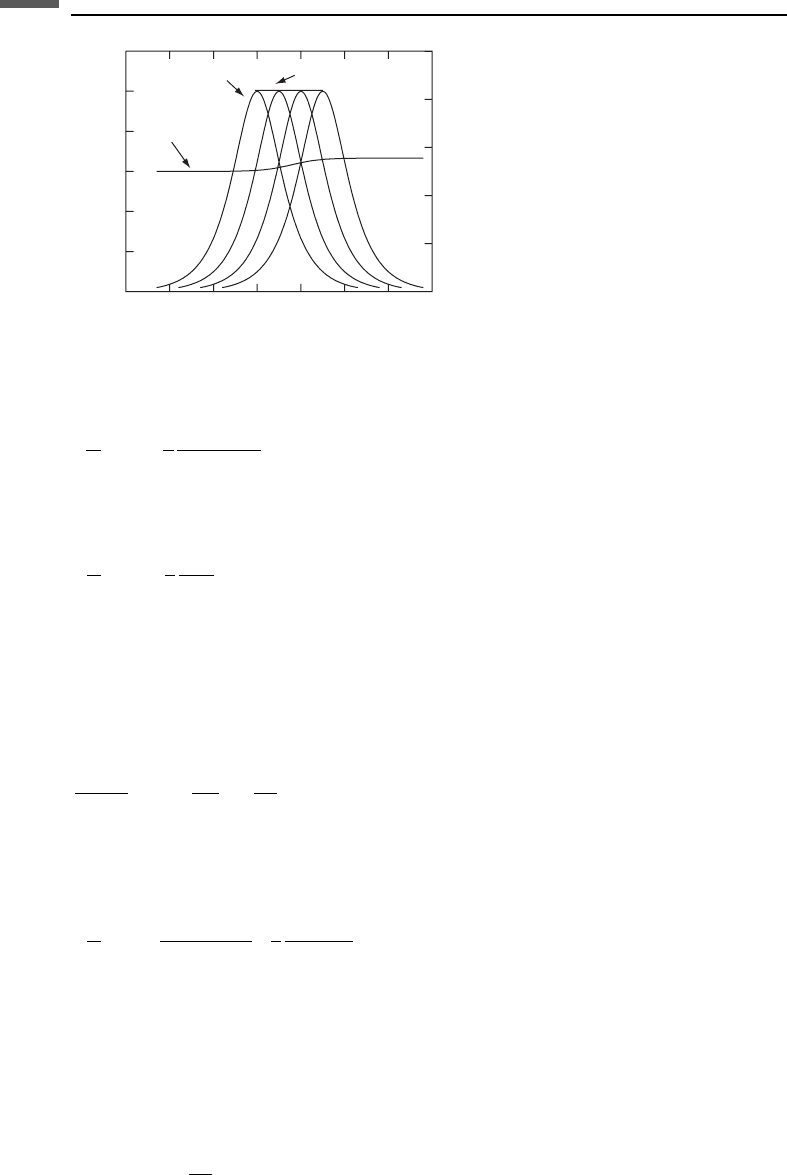
Similarly we can write Q as a function of frequency (Figure 3.8.3):
1
Q
¼
M
I
ðoÞ
M
R
ðoÞ
1
Q
¼
E
2
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
E
1
ðE
1
þ E
2
Þ
p
o=o
r
ðÞ
1 þ o=o
r
ðÞ
2
The maximum attenuation
1
Q
max
¼
1
2
E
2
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
E
1
ðE
1
þ E
2
Þ
p
0
0.1
0.2
0.3
0.4
0.5
0.6
0
0.4
0.8
1.2
1.6
2
−5
05
1/Q (∆M/M )
Modulus
log(w/w
r
)
1/Q
M
∆M
Figure 3.8.3 Schematic of the standard linear solid in the frequency domain.
125 3.8 Viscoelasticity and Q
1
Q
max
¼
1
2
M
1
M
0
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
M
1
M
0
p
occurs at o = o
r
. This is sometimes written as
1
Q
max
¼
1
2
M
M
ð3:8:7Þ
where M=
M ¼ðM
1
M
0
Þ=
M is the modulus defect and
M ¼
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
M
1
M
0
p
:
Liu et al. (1976) considered the nearly constant Q model in which simple
attenuation mechanisms are combined so that the attenuation is nearly a constant
over a finite range of frequencies (Figure 3.8.4). One can then write
VðoÞ
Vðo
0
Þ
¼ 1 þ
1
Q
ln
o
o
0
which relates the velocity dispersion within the band of constant Q to the value of Q
and the frequency. For large Q, this can be approximated as
1
Q
max
log o=o
0
ðÞ
1
2
M M
0
M
0
ð3:8:8Þ
where M and M
0
are the moduli at two different frequencies o and o
0
within the band
where Q is nearly constant. Note the resemblance of this expression to equation
(3.8.7) for the standard linear solid.
Kjartansson (1979) considered the constant Q model in which Q is strictly
constant (Figure 3.8.5). In this case the complex modulus and Q are related by
MðoÞ¼M
0
io
o
0
2
0
0.1
0.2
0.3
0.4
0.5
0.6
0
0.4
0.8
1.2
1.6
2
−6 −4 −2
02468
1/Q (∆M/M)
Modulus
log(w)
1/Q
M
nearly constant
Figure 3.8.4 Schematic of the nearly constant Q model in the frequency domain.
126 Seismic wave propagation
