Маслов А.В., Григорьева А.А. Математическое моделирование в экономике и управлении: Учебное пособие. Гриф УМО
Подождите немного. Документ загружается.

Анализ сетевого графика по критерию времени. Критический путь,
время, критические работы.
Алгоритм расчёта ранних сроков начал и окончаний работ
(алгоритм Форда).
Алгоритм построения критического пути.
Расчёт временных параметров сетевого графика.
Управление ходом работ с помощью рассчитанных параметров
сетевого графика.
Алгоритм расчёта параметров сетевого графика с вероятностным
временем выполнения операций.
Два способа отыскания оптимальных вариантов сетевого графика
по имеющейся информации прироста затрат на один день ускорения
работ.
Возможность и эффективность применения сетевых методов для
управления сложными системами в сфере экономики.
171

Тема 11 Задачи упорядочения. Задачи управления запасами.
Задачи замены оборудования
Задачи упорядочения – это задачи определения оптимальной
последовательности обработки изделий, массивов информации,
определения наилучших маршрутов движения и т д.
Классификация задач упорядочения
По наличию того или иного признака задачи упорядочения можно
подразделить следующим образом:
1. По характеру обслуживания требований – на
детерминированные и вероятностные (стохастические). Если
продолжительность операций предполагается точно известной, то
имеем детерминированную задачу упорядочения, в противном случае –
вероятностную (стохастическую).
2. По характеру учёта времени – на динамические и статические.
Если процесс упорядочения с течением времени меняет свой характер,
то имеем динамическую задачу упорядочения, в противном случае –
статическую.
Детерминированная задача упорядочения
Постановка задачи и выбор критерия оптимизации
Пусть имеется несколько изделий, каждое из которых должно быть
обработано на двух машинах. Допустим, что известны время обработки
и последовательность обработки каждого изделия на каждой машине
(табл. 11.1).
Таблица 11.1
Исходные данные и решение задачи упорядочения
Номер изделия
j
1 2 3 4 5 6
Время обработки на 1-й машине
j
t
1
6 4 6 5 7 4
Время обработки на 2-й машине
j
t
2
5
2
3
6 6 7
Номер цикла 4 1 2 4 5 3
Требуется выбрать такой порядок обработки изделий, при котором
суммарное время обработки изделий будет минимальным (или
суммарное время ожидания обработки изделий на 2-й машине).
172
Выявление основных особенностей, взаимосвязей и
количественных закономерностей
Перечислим основные ограничения задачи:
время перехода изделия от одной машины к другой незначительно
и им можно пренебречь;
каждое изделие обрабатывается в определённом технологическом
порядке;
каждое обслуживание должно быть завершено прежде, чем
начнётся следующее.
Обозначим:
j
t
1
– время обработки j-го изделия на первой машине;
j
t
2
– время обработки j-го изделия на второй машине.
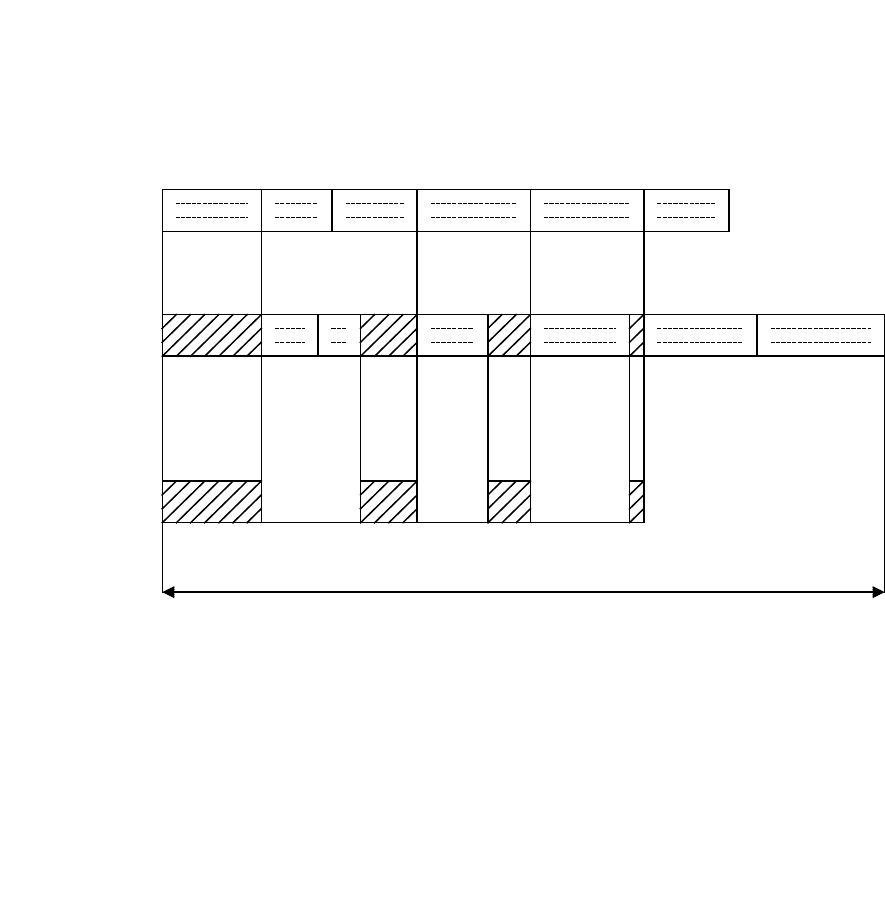
Изобразим процесс обработки изделий на двух машинах
графически:
Время обра-
ботки
на машине 1
Время обра-
ботки
на машине 2
Время
простоя
машины 2
Рис. 11.1. Процесс обработки изделий на двух машинах
(Гантт – карта)
На рис.11.1
Т
– полное время, которое пройдёт от начала
обработки первого изделия на первой машине до конца обработки
последнего изделия на второй машине.
Построение математической модели
Пусть
nj
t
время простоя второй машины между концом
выполнения работы по обработке (j-1)-го изделия на второй машине и
началом обработки j-го изделия на той же самой машине.
Тогда суммарное время обработки изделий составит:
173
6 5 7
4
6
11
t
4
12
t
13
t
14
t
15
t
16
t
2
3 6 6 7
2221
t5t
23
t
24
t
25
t
26
t
6 3
2 1
1n
t
2n
t
3п
t
4п
t
T

411229
1 1
2
m
j
m
j
njj
ttT
, а т.к. сумма
m
j
j
t
1
2
постоянна, то
подлежит минимизации
m
j
nj
t
1
(в нашем случае
12
6
1
j
nj
t
).
Исследование математической модели
Известен весьма простой алгоритм для нахождения оптимальной
последовательности порядка обслуживания m требований на двух
пунктах обслуживания (алгоритм Джонсона).
При этом каждое из требований должно пройти сначала
обслуживание на первом пункте, а затем на втором. Продолжительности
обслуживания требований различные. Если использовать метод прямого
перебора, то при наличии m требований (изделий) и двух пунктов
обслуживания (машин) и при условии, что все виды требований
обрабатываются в одинаковом порядке, существует m! возможных
вариантов (последовательностей). Для нашего примера имеется 720
вариантов.
Алгоритм Джонсона включает следующие основные этапы:
поиск наименьшего элемента. Ищем в таблице наименьший
элемент (равен 2, относится ко второй машине) и отмечаем точкой;
перестановка изделий. Определяется местонахождение элемента.
Если этот элемент относится к первой машине, то столбец с точкой
поставить на первое место, если ко второй, то поставить на последнее
место календарного плана. При наличии равных минимальных
элементов в обеих строках изделие с минимальным временем обработки
на первой машине ставится на первое место, а на второй машине – на
последнее место. Если же одинаковые минимальные элементы
оказываются в первой (второй) строке, то на первое (последнее) место
ставится изделие, которому соответствует меньший элемент второй
(первой) строки.
вычёркивание из таблицы столбца, отмеченного точкой, и
возвращение к пункту 1 и т. д., пока не будет исчерпан список всех изделий.
В результате получим оптимальную последовательность обработки
изделий на двух машинах. Последняя графа таблицы 11.1 (номер цикла)
показывает последовательность вычёркивания столбцов для данного
примера.
В некоторых частных случаях алгоритм Джонсона применяется и
для решения задач упорядочения, требующих трехэтапного
обслуживания. Это можно сделать, когда соблюдается одна из
следующих систем неравенств:
174
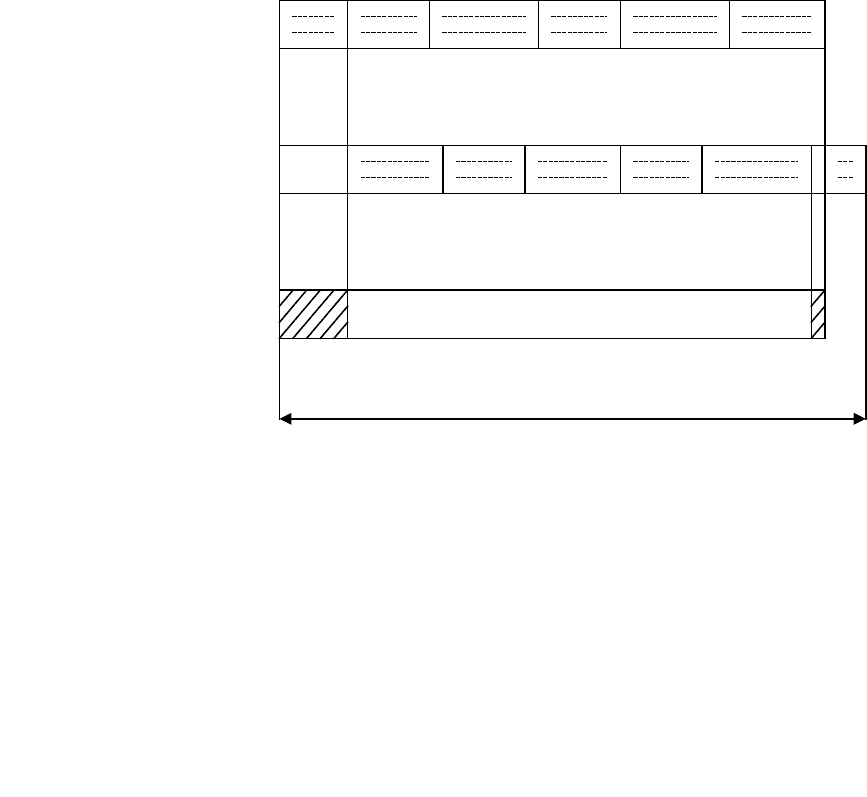
Время обработки
на машине 1
Время обработки
на машине 2
Время простоя
машины 2
Рис. 11.2. Процесс оптимальной обработки изделий на двух машинах
минимальное время обработки изделия на первой машине больше
или равно максимальному времени обработки изделия на второй машине:
j
mj
j
mj
tt
2
,...,1
1
,...,1
max
min
;
минимальное время обработки изделий на третьей машине больше
или равно максимальному времени обработки на второй машине:
j
mj
j
mj
tt
2
,...,1
3
,...,1
max
min
.
После этого составляется новая таблица для суммы
jj
tt
21
вместо
j
t
1
или
jj
tt
32
вместо
j
t
2
, и к ней применяется алгоритм Джонсона.
Класс задач, к которым применим алгоритм Джонсона, ограничен.
Решение же методом прямого перебора всех возможных вариантов уже
при десяти изделиях требует более 3 млн. переборов. В некоторых
задачах упорядочения для решения можно использовать методы
линейного и динамического программирования.
Задачи управления запасами
Можно выделить четыре основные причины, приводящие к
необходимости образования запасов:
необходимость гарантирования бесперебойности
производственного процесса;
периодичность производства отдельных сорторазмеров
материальных ресурсов у поставщиков;
175
4
16
t
14
t
15
t
11
t
13
t
12
t
7
26
t
25
t
21
t
22
t
5 7 6 6
4
1п
t
6
6
5 3
2
1
2
п
t
341429
min
T
особенности транспортировки от поставщика до потребителя
(несоответствие грузоподъёмности транспортных средств и размеров
потребления);
несовпадение ритма производства и поставок производимых
ресурсов с ритмом их потребления.
Задача управления запасами в общем случае формулируется так.
Имеются некоторые запасы, затраты на хранение которых являются
функцией (линейной или нелинейной) их величины. Известны также
затраты на доставку ресурсов. Необходимо определить оптимальный
размер поставки, частоту или сроки поступления ресурсов с тем, чтобы
суммарные издержки были минимальны. Критерием оптимизации
является минимизация суммы издержек на хранение и поставку
ресурсов.
В общем случае задачи управления запасами сводятся к задачам
нелинейного программирования, общих методов решения которых нет.
Классификация задач управления запасами
Задачи управления запасами по наличию того или иного признака
можно разделить:
1. По количеству управляемых периодов (пополнения запасов) – на
однопериодные и многопериодные. Если пополнение запасов
производится в системе один раз, такая задача управления запасами
называется однопериодной, в противном случае – многопериодной. Так,
например, автомашина может один раз заправиться и сделать ещё
дополнительный запас горючего или у неё есть возможность
подзаправляться во время перевозок.
2. По характеру пополнения запасов – с непрерывной системой
пополнения запасов (мгновенной) и периодической (с задержкой). Если
при уменьшении запаса до определённого уровня происходит его
пополнение, то мы имеем задачу с непрерывном пополнением запасов.
При этом необходим постоянный контроль за уровнем запаса.
Разновидностью такой системы является система "двух бензобаков"
("двух бункеров", "двух складов"). Один из бензобаков (бункеров,
складов) выдает запас (горючее) только в том случае, если кончается
запас в другом, одновременно подаётся сигнал о необходимости
пополнения бензобаков (бункеров, складов).
3. По учёту характера спроса – на детерминированные и
вероятностные (стохастические). Если невозможно точно предсказать
спрос с момента поступления запаса до момента его пополнения, то
имеем вероятностную задачу управления запасами, в противном случае
– детерминированную. Так, если неизвестен маршрут движения
176

автомашины (состояние дороги, уклоны, подъёмы и т. д.), то
практически невозможно точно предсказать расход горючего.
4. По количеству типов ресурсов – на однопродуктовые и
многопродуктовые. Если запас включает несколько видов продукции, то
имеем многопродуктовую задачу управления запасами, в противном
случае – однопродуктовую. Так, если для автомашины кроме бензина
будем учитывать расход масла, то это уже будет многопродуктовая
задача управления запасами.
5. По виду целевой функции – на задачи с пропорциональными и
непропорциональными затратами. Если издержки производства на
единицу продукции постоянны, и весь объём спроса в конечном счете
удовлетворяется, то мы имеем дело с пропорциональными затратами, в
противном случае – с непропорциональными. Так, затраты на 1 км
пробега автомашины могут быть постоянными, а могут быть
переменными (например, зависят от дальности ездки).
Однопродуктовая детерминированная задача управления запасами
Постановка задачи и выбор критерия оптимизации
Пусть месячная потребность предприятия в каком-либо материале
(песок, щебень, цемент и т.д.) составляет Q условных единиц. Расход
этого материала во времени происходит равномерно. Необходимо
определить, каков должен быть размер поставки материала, чтобы
суммарные затраты на создание и хранение запаса были минимальны.
Выявление основных особенностей, взаимосвязей и
количественных закономерностей
Обозначим
х
С
затраты на хранение единицы запаса в единицу
времени, а
д
С
затраты на доставку партии материалов. Пусть затраты
д
С
не зависят от количества материалов в поставленной партии.
Предполагается, что все партии состоят из одинакового числа единиц
материала,
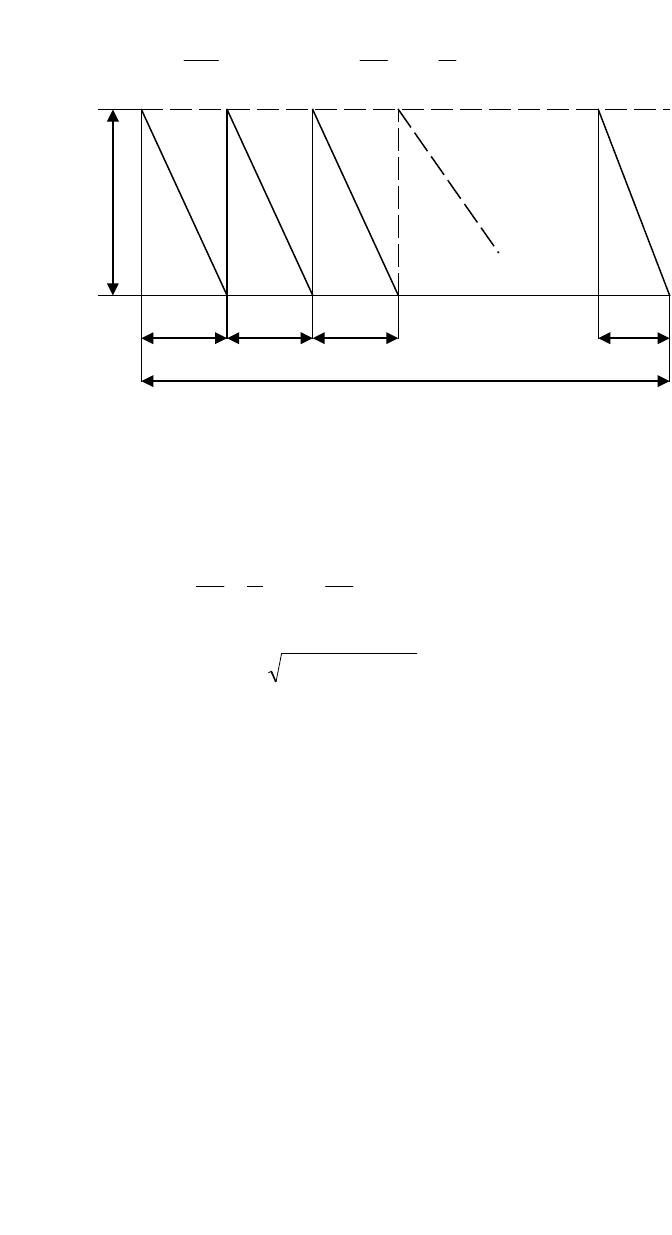
S
величина поставок. Изобразим графически движение
запасов в течение времени (месяца)
Т
. Обозначим
t
промежуток
времени (период) от момента поставок партии материала до момента её
израсходования. Количество необходимых поставок для
удовлетворения месячной потребности в материале:
tTSQn //
.
177
Построение математической модели
Суммарные месячные расходы на хранение материала и доставку
за период
Т
:
дxдx
C
S
Q
C
ST
nCC
tS
Y
22
.
Рис. 11.3. Движение запасов с мгновенным временем их пополнения
Исследование математической модели
Продифференцировав целевую функцию относительно S и
приравняв производную
dSdY /
к нулю, получим
0
2
2
дx
C
S
Q
C
T
dS
dY
,
откуда
xдonm
CTQCS /2
.
Это выражение носит название формулы Кампа, из которой можно
установить оптимальный размер поставок. С помощью этой формулы
можно определить и оптимальные моменты времени пополнения запасов.
Теперь усложним задачу, будем учитывать убытки, если спрос не
удовлетворён.
Задача управления запасами с учётом убытков
из-за неудовлетворённого спроса
Постановка задачи
Пусть на предприятии вследствие неудовлетворённого спроса
возникают убытки, характеризующиеся величиной
y
С
на единицу
ресурса в единицу времени. В течение времени
1
t
каждого периода
t
уровень запаса достаточен для удовлетворения спроса, а затем в течение
интервала
2
t
запас отсутствует, причём неудовлетворённый спрос
покрывается из следующей партии с момента поступления на склад.
Пусть потребность в материале составляет
Q
единиц в период
T
.
178
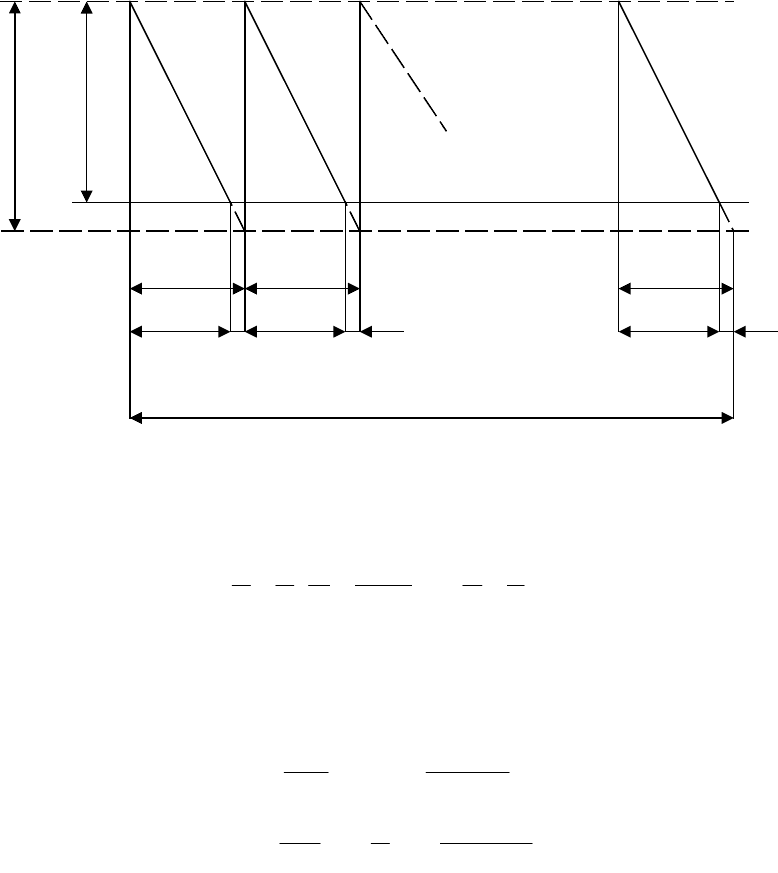
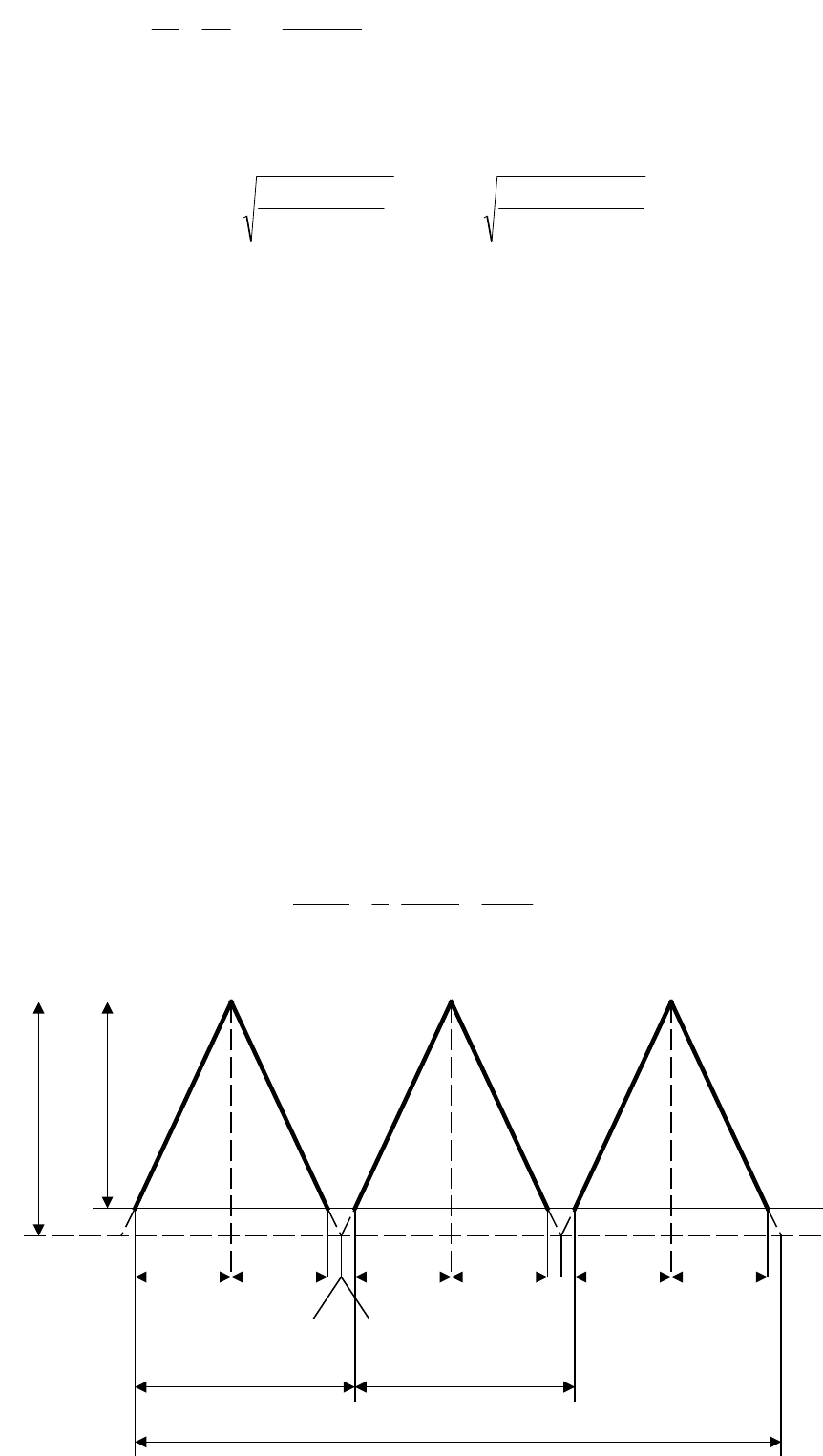
S
t t t t
T
Определить, какими должны быть поставляемая S и потребная V
партии, чтобы затраты на доставку и хранение с учётом
неудовлетворённого спроса были минимальными.
Выявление основных особенностей, взаимосвязей и
количественных закономерностей
Обозначения те же, что и ранее. Графически движение запасов при
неполном удовлетворении спроса представлено на рис. 11.4.
Рис.11.4. Движение запасов с учётом убытков
из-за неудовлетворённого спроса
По графику легко составить следующие закономерности:
. ; ;
21
t
T
V
Q
n
V
SV
t
t
V
S
t
t
.
Построение математической модели
Суммарные затраты на хранение, доставку и потери из-за
неудовлетворённого спроса за период T:
.
22
22
1
2
2
2
yдx
yдx
C
V
TSV
C
V
Q
C
V
TS
nC
tSV
CC
S
Y
Исследование математической модели
Чтобы определить минимум функции, находим частные
производные от Y по S и V и приравняем их к нулю:
179
S
V
t t t
1
t
1
t
1
t
2
t
2
t
T
.0
2
2
2
;0
2
2
22
2
yд
x
yx
С
V
TSVTVSV
C
V
Q
V
TCS
V
Y
C
V
TSV
C
V
ST
S
Y
Решив систему уравнений, получим:
;
2
yxx
yд
опт
CCTC
CQC
S
yx
yxд
опт
CTC
CCQC
V
2
.
Общая детерминированная многопериодная
задача управления запасами
Постановка задачи и выбор критерия оптимизации
Пусть месячная потребность предприятия, в каком-либо материале
составляет Q условных единиц. Расходуется материал равномерно. При
неудовлетворении спроса на предприятии возникают убытки,
измеряемые величиной
у
С
на единицу материала в единицу времени.
Затраты на хранение единицы материала в единицу времени составляют
х
С
. Затраты на поставку партии материала –
д
С
. В течение периодов
41
,tt
происходит поставка материала предприятию. Определить
оптимальные размеры поставляемой и потребной партии материала,
минимизирующие затраты на доставку и хранение.
Выявление основных особенностей, взаимосвязей и
количественных закономерностей
Представим графически движение запасов при неполном
удовлетворении спроса и с задержкой пополнения запасов (рис. 11.5).
Из графика можно установить следующие соотношения:
. ;
43
21
V
SV
t
tt
V
S
t
tt
Построение математической модели
Суммарные затраты на хранение, доставку и потери из-за
неудовлетворённого спроса за период T:
180
V
S
T
t t
1
t
2
t
3
t
1
t
2
t
1
t
2
t
