Маслов А.В., Григорьева А.А. Математическое моделирование в экономике и управлении: Учебное пособие. Гриф УМО
Подождите немного. Документ загружается.

объединяемых в смешанную. Если смешанные стратегии входят в число
оптимальных, то вероятности использования входящих в них чистых
стратегий равны между собой.
Рассмотрим матрицу С, разбитую на четыре подматрицы, для
которых выполняется условие равенства сумм элементов по строкам и
столбцам:
C=
3511
5311
1111
4220
2402
.
Объединяя стратегии А
1
, А
2
, и А
3
, А
4
и А
5
, В
1
и В
2
, В
3
и В
4
, приводим
матрицу к виду:
4 1
0
1
40
11
С
Полученная матрица содержит седловую точку. Поэтому решение
первоначальной игры, заданной матрицей С, таково: Р*=(1/3; 1/3; 1/3; 0;
0), Q*=(1/2; 1/2; 0; 0). Цена игры равна единице. В результате
упрощения игры решение её стало очевидным: оптимальной для игрока
А является комбинация стратегий А
1
, А
2
и А
3
, а для игрока В комбинация
стратегий В
1
и В
2
. Вероятности применения стратегий А
1
, А
2
и А
3
равны
между собой, сумма их равна 1, поэтому Р*=(1/3; 1/3; 1/3; 0; 0).
Аналогично, оптимальная стратегия игрока В имеет вид Q*=(1/2; 1/2; 0; 0).
Таким образом, при решении игры mxn следует:
а) проверить, содержит ли матрица седловую точку;
б) если седловой точки нет, то сравнить между собой элементы
строк и столбцов для исключения дублирующих и доминирующих стратегий;
в) рассмотреть возможность разбиения матрицы на подматрицы
для замены некоторых групп чистых стратегий смешанными.
Как уже упоминалось, в условиях полной неопределённости
действует уже так называемая теория стратегических решений. В
рассмотренных выше задачах теории игр предполагалось, что в них
принимают участие два участника, интересы которых противоположны.
Поэтому действия каждого игрока направлены на увеличение выигрыша
(уменьшение проигрыша). Однако во многих задачах, приводящихся к
игровым, неопределённость вызвана отсутствием информации об
условиях, в которых осуществляются действия.
Эти условия зависят не от сознательных действий другого игрока, а
от объективной действительности, которую принято называть
природой. Такие игры называются играми с природой. Решения в этих
141
1
2
3
5
4
6

играх получают с помощью теории стратегических решений. Человек А
в играх с природой старается действовать осмотрительно, используя
например, минимаксную стратегию, позволяющую получить
наименьший проигрыш. Второй игрок В (природа) действует
совершенно случайно, возможные стратегии определяются как её
состояния (например, условия погоды в данном районе, спрос на
определённую продукцию, объём перевозок, некоторое сочетание
производственных факторов и т.д.). В некоторых задачах для состояний
природы может быть задано распределение вероятностей, в других – и
оно неизвестно.
Условия игры, как и в рассмотренных выше задачах теории игр,
задаются в виде матрицы:
C=
mnmm
n
n
ccc
ccc
сcc
...
............
...
...
21
22221
11211
.
Элемент с
ij
равен выигрышу игрока А, если он использует
стратегию А
i
, а состояние природы – В
j
.
В ряде случаев при решении игр рассматривают матрицу рисков R.
Элемент матрицы r
ij
представляет собой разность между выигрышем,
который получил бы игрок А, если бы он знал состояние природы B
j
, и
выигрышем, который он получит в тех же условиях, применяя
стратегию A
i
, т.е. r
ij
=
j
- с
ij
, где
ijj
c
i
max
.
Рассмотрим ряд критериев, используемых при решении игр с
природой. Все они основаны на принципе, на основании которого
неопределённые ситуации преобразуются в детерминированные и
которые решаются ранее рассмотренными методами (одним из них
является принцип минимакса). Однако здесь принцип минимакса
(осторожности) будет чрезмерно пессимистическим – это стратегия
перестраховщиков. При использовании принципа минимакса не
учитывается априорная информация о состоянии природы и тем самым
ограничивается тот выигрыш, который эта информация может дать.
Два следующих критерия используются, когда вопрос
распределения вероятностей состояний природы не решён.
Максиминный критерий Вальда – это критерий, который совпадает
с критерием выбора стратегии, позволяющим получить цену игры для
двух лиц с нулевой суммой. Согласно этому критерию выбирается
стратегия, гарантирующая при любых условиях выигрыш не меньший,
чем
ij
c
j
i
min
max
.
142
1
2
3
5
4
6
Критерий минимального риска Сэвиджа – это критерий,
рекомендующий выбирать стратегию, при которой величина риска
принимает наименьшее значение в самой неблагоприятной ситуации,
т.е.
ij
r
i
j
max
min
. Принцип Сэвиджа состоит в том, чтобы не допустить
чрезмерно высоких потерь, к которым могут привести ошибочные
решения. Его применяют особенно часто при принятии менеджерами
управленческих решений в каких-то ответственных случаях.
Представляется логичным при выборе стратегии вместо двух
крайних взглядов выбрать промежуточный.
Как критерий Вальда, так и критерий Сэвиджа основаны на самой
пессимистической оценке обстановки. В отличие от них критерий
Гурвица учитывает как пессимистический, так и оптимистический
подход к ситуации. Такого рода компромиссное правило, определяющее
выбор решения в условиях полной неопределённости, когда
распределение вероятностей состояний природы неизвестно,
заключается в том, что неразумно, приняв во внимание самый
маленький выигрыш, не учитывать самый большой, для чего
субъективным образом вводится некоторый коэффициент оптимизма
(он выполняет роль вероятности). Этот принцип часто называется
обобщённым максимином. Принимается решение о выборе стратегии,
при которой имеет место
ij
c
j
ij
c
ji
min
)1(
maxmax
, где 0
1.
Значение
выбирают на основании субъективных соображений.
Чем больше желание подстраховаться в данной ситуации, тем ближе
к нулю следует брать значение
. Применим принцип Гурвица к
решению примера:
Таблица 9.4
Применение принципа Гурвица к игре из примера 9.1
A
i
B
j
min
выигр
ыш
max
выигрыш
Расчётный выигрыш
при
B
1
B
2
B
3
B
4
А А
=0,4
=0,2
1
A
35 35 3 10 3 35 15,8 9,4
2
A
24 1 6 90 10 90 36,6 18,2
3
A
40 60 10 15 1 60 42 20
По принципу обобщённого максимина необходимо стороне А
использовать стратегию А
3
.
143
1
2
3
5
4
6
Кроме перечисленных принципов (минимакса, обобщённого
максимина и минимальных потерь), используют принцип Байеса-
Лапласа, который отступает от условий полной неопределённости. При
этом предполагается, что возможным состояниям природы В
1
, В
2
, …, B
n
можно приписать определённую вероятность, соответственно равную
q
1
, q
2
,…, q
n
. Этот принцип используется, если есть возможность
определить вероятность возникновения отдельных состояний природы
(например, статистическая обработка метеосводок), если нет –
применяют принцип равновероятности (принцип недостаточного
основания Лапласа). Он заключается в том, что всем возможным
состояниям природы приписывается одинаковая вероятность, и
решение игры ищется при таких условиях. Однако во всех случаях
нельзя утверждать, что принятое решение оптимальное, оптимальным
оно является только относительно принятого распределения
вероятностей состояний природы.
В заключение можно отметить, что если мы имеем дело с
многократно повторяющимися состояниями и многократно
повторяющимися решениями, то наиболее целесообразно применять
принцип Байеса- Лапласа или Гурвица. В случае разового решения
применяют обычный принцип минимакса или минимальных потерь
(Сэвиджа).
Принципиальным достоинством теории игр считают то, что она
расширяет общепринятое понятие оптимальности, включая в него такие
важные элементы, как, например, компромиссное решение,
устраивающее разные стороны в подобном споре (игре).
На практике же игровые подходы используются экономистами при
разработке макроэкономических моделей, в которых учитываются
интересы различных звеньев (например, отраслей и экономических
районов). Кроме того, математические приёмы теории игр могут
применяться для решения многочисленных практических
экономических задач на промышленных предприятиях. Например, для
выбора оптимальных решений в области повышения качества
продукции или определения запасов. Противоборство здесь происходит
в первом случае между стремлением выпустить больше продукции
(затратить на неё меньше труда) и сделать её лучше, т.е. затратить
больше труда, во втором случае – между желанием запасти ресурсов
побольше, чтобы быть застрахованным от случайностей, и запасти
поменьше, чтобы не замораживать средства. Желающим подробнее
разобраться отсылаем к литературе.
Вопросы для самопроверки
144
1
2
3
5
4
6
Предмет изучения теории игр.
Виды причин неопределённости результата игры.
Основные понятия теории игр: игра, правила, ход, стратегия,
оптимальная стратегия.
Виды игр.
Общая постановка игры двух лиц с нулевой суммой.
Понятия нижней и верхней цены игры, соответствующих
стратегий, седловой точки платёжной матрицы, смешанной
стратегии, оптимальной смешанной стратегии.
Общая постановка задачи теории игр, её математическая модель,
формулы для получения оптимальных вероятностей
использования стратегий.
Основная теорема теории игр.
Геометрический способ решения задач теории игр.
Метод Брауна приближённого решения задач теории игр.
Сведение игры к задаче линейного программирования.
Способы упрощения платёжной матрицы игры.
Понятие игр с природой.
Виды критериев, используемых при решении игр с природой.
Применение теории игр в экономических исследованиях.
Ваши предложения по усовершенствованию сценариев деловых
игр, алгоритмов научных экономических исследований и т. д..
Тема 10 Основы сетевого планирования и управления
Сетевое планирование применяют для организации и составления
календарных планов реализации больших комплексов работ. Это,
например, научно – исследовательские работы с участием нескольких
институтов, разработка автоматизированной системы бухгалтерского
учёта, строительство большого объекта, освоение производства новой
машины, планирование и осуществление космических исследований и т
д. Во всех указанных случаях выполняется огромное количество
взаимозаменяемых операций, в работу вовлекается множество людей,
предприятий, организаций; управление осложняется новизной
145
1
2
3
5
4
6
разработки, трудностью точного определения сроков и предстоящих
затрат. В управлении сложными разработками высокоэффективными
оказались сетевые методы, получившие широкое распространение.
Использование этих методов позволяет сравнительно просто выяснить,
когда необходимо начинать и заканчивать выполнение отдельных
операций, как задержка хода выполнения некоторой операции влияет на
время завершения всего проекта.
Для использования сетевых методов нужно, прежде всего, разбить
крупный проект на отдельные операции (работы) и составить перечень
операций. Некоторые из них могут выполняться одновременно, другие
– только в определённом порядке. Например, при строительстве дома
нельзя возводить стены раньше, чем сделан фундамент. Необходимо
выяснить очерёдность выполнения всех операций списка.
Для этого составляем список операций, непосредственно
предшествующих каждой операции. После этого нужно запланировать
время, необходимое для выполнения каждой операции. Полученные
данные обычно помещаются в таблицу.
Пример 10.1.
Таблица 10.1
Исходные данные гипотетического проекта
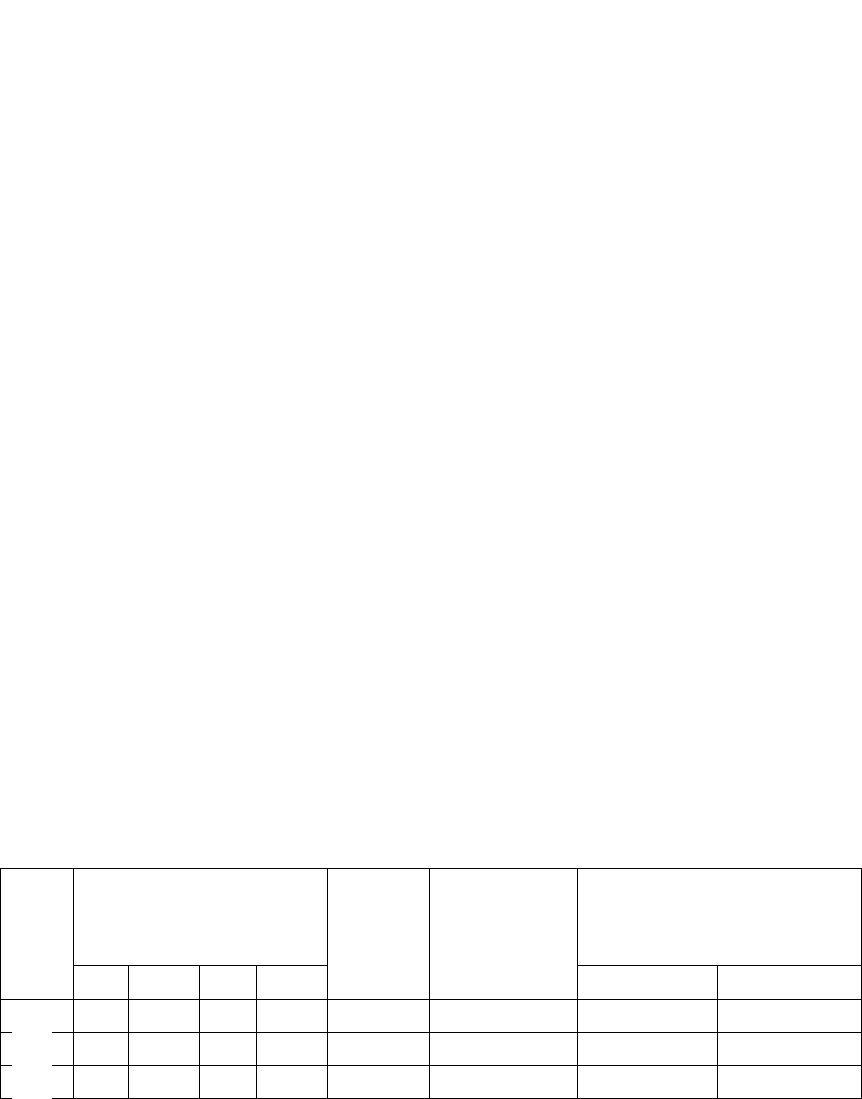
Операция Предшествующие операции Время
1
– 10
2
– 5
3
– 15
4
21
,
18
5
32
,
19
6
54
,
18
В таблице приведены данные для проекта, состоящего из шести
работ. Для каждой из них задана продолжительность и указаны
непосредственно предшествующие ей операции. Можно построить по
этим данным сетевой график, или граф. Но сначала несколько
терминов из теории графов. Граф – это совокупность двух конечных
множеств: множества точек, которые называются вершинами, и
множества пар вершин, которые называются рёбрами.
146
1
2
3
5
4
6
4
P
3
P
2
P
1
P
5
P
1
3
4
5
6
2
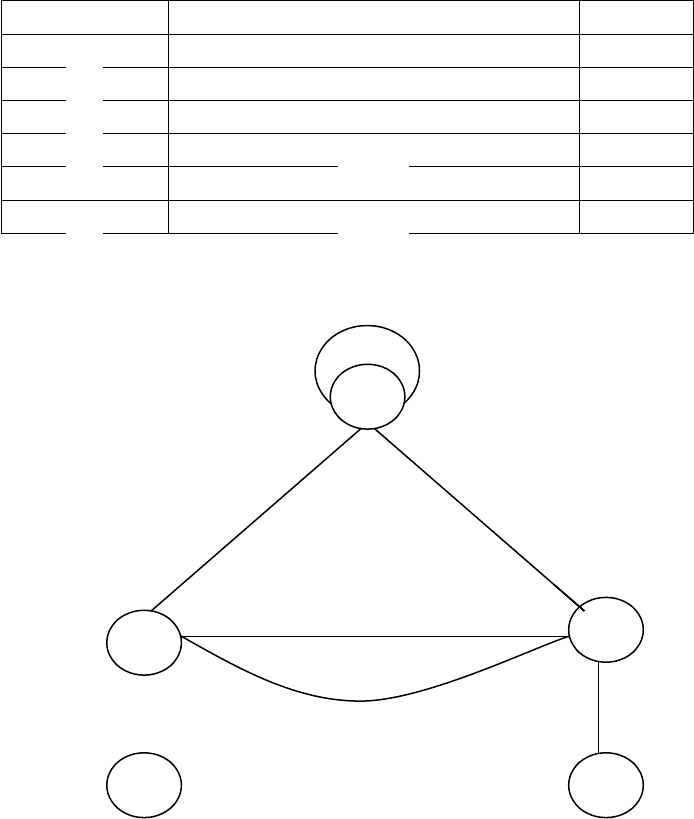
Рис. 10.1. Пример графа
Это пример графа, имеющего пять вершин и шесть ребёр. Если
рассматривать множество упорядоченных пар точек, т.е. на каждом
ребре задано направление, то граф называется ориентированным. В
противном случае – неориентированном графом.
Рёбра, имеющие одинаковые концевые вершины, называются
параллельными. Ребро, концевые вершины которого совпадают,
называется петлёй. На рис. 10.1
4
и
5
- параллельные ребра,
2
- петля.
Граф называется полным, если любые две его различные вершины
соединены ребром, и он не содержит параллельных рёбер.
Путём в графе называется такая последовательность рёбер,
ведущая от некоторой начальной вершины P
1
в конечную вершину P
n
, в
которой каждые два соседних ребра имеют общую вершину, и никакое
ребро не встречается более одного раза. Например, в графе-примере
последовательность рёбер (
1
,
2
,
3
,
4
,
5
,
6
) образует путь, ведущий
от вершины P
1
к вершине P
4
.
Циклом называется путь, начальная и конечная вершины которого
совпадают. На рис. 10.1 образуют цикл рёбра (
1
,
3
,
4
).
Длиной пути или цикла называется число рёбер этого пути или
цикла.
В ориентированных графах на рёбрах задано направление, т.е. у
каждого ребра фиксируется начало и конец. Такие направленные рёбра
называются дугами.
Сетью называется граф, каждой дуге которого поставлено в
соответствие некоторое число (или несколько чисел), обычно это время.
Таким образом, при построении графа каждую операцию
изображают в виде ориентированной дуги. Связи между операциями
также представляют в виде дуги. Дугу-связь проводят из конца дуги,
147
1
2
3
5
4
6
соответствующей предшествующей операции, в начало следующей
операции.
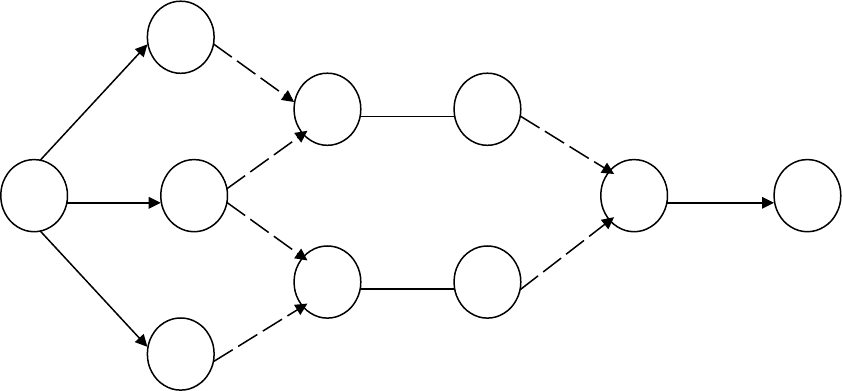
Рис.10.2. Сетевой график комплекса работ
Чтобы отличить операции от связей, операции изображают
сплошными линиями, а связи – пунктирами. Вершины графа называют
событиями. Временем наступления события считают время, когда
завершено выполнение всех операций, входящих в соответствующую
вершину.
Таким образом, граф, представляющий взаимосвязь отдельных
работ проекта, называется сетевым графиком. На рис. 10.2 построен
сетевой график для комплекса операций, заданных таблицей из
предыдущего примера.
Главными элементами сетевого графика являются события и
работы. Событие – это состояние, момент достижения промежуточной
или конечной цели разработки (начальное событие – отправной момент
разработки). Событие не имеет протяжённости во времени. Работа –
это протяжённый во времени процесс, необходимый для свершения
события. Любая работа имеет предшествующее событие и
определённым событием заканчивается.
После первоначального составления сетевого графика необходимо
проверить его соответствие некоторым обязательным требованиям:
Только начальные события не имеют входящих стрелок, только
конечные события – выходящих. Если событие по своему характеру
является промежуточным, оно должно иметь как входящие, так и
выходящие стрелки.
Каждая работа должна иметь предшествующее и завершающее события.
148
1
2
3
5
4
6
1
a
2
a
3
a
4
a
5
a
6
a
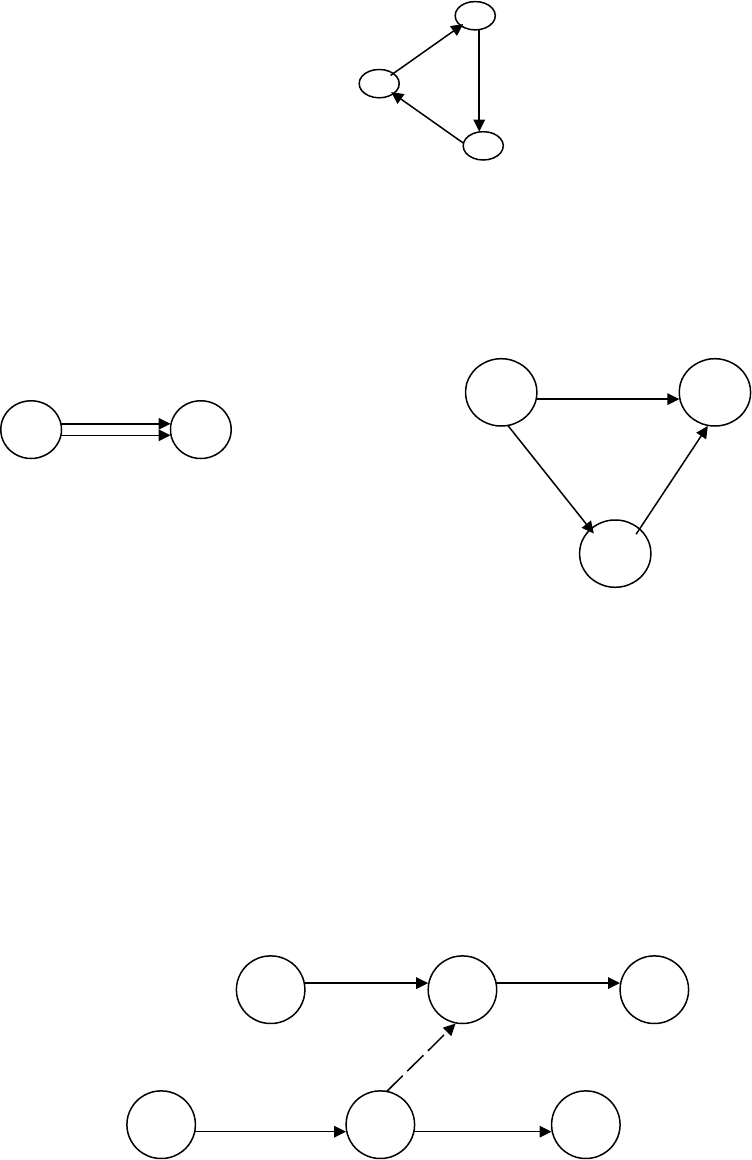
На графике не должно быть изолированных участков, не связанных
работами с остальной частью графика.
На графике не должно быть контуров (циклов) и петель, т.к. они,
по существу, означают, что условием начала некоторой работы является
её же окончание.
Рис. 10.3. Пример контура
При возникновении контура (а в сложных сетях это случается
достаточно часто) необходимо вернутся к исходным данным и путём
пересмотра состава работ добиться его устранения.
Рис. 10.4. Пример введения фиктивного события для устранения
параллельности работ
Любые два события должны быть непосредственно связаны не
более чем одной работой. При обнаружении на графике параллельных
работ вводится необходимое число фиктивных событий (в нашем
примере одно – 2') и соответствующее число фиктивных работ
(рис.10.4), и одна из параллельных работ замыкается на это фиктивное
событие.
149
1
2
3
5
4
6
1 2
1 2
2'
a
b
c

Рис. 10.5. Пример введения фиктивной работы
Таблица 10.2
Перечень событий и работ для составления сетевого графика
примера 10.2
Работы
Событие
предшествующее Завершающее
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
1
1
1
2
3
3
4
4
4
5
6
6
7
7
7
8
9
2
3
4
5
4
6
5
6
7
8
7
9
8
9
10
10
10
Это один из случаев, когда требуется введение фиктивных работ и
событий.
Второй случай – отражение зависимости событий, не связанных
реальными работами. Предположим, например, что работы a и b (см.
рис. 10.5) могут выполняться независимо друг от друга, но требуют
одного и того же оборудования, так что работа b не может начаться,
пока не освободится оборудование с окончанием работы a. Это
обстоятельство требует введения фиктивной работы c (рис.10.5).
Третий случай – неполная зависимость работ. Например, работа c
требует для своего начала завершения работ a и b, но работа d связана
только с работой b, а от работы a не зависит.
Тогда требуется введение фиктивной работы m и фиктивного
события
'3
, как показано на рис. 10.6.
150
1
2
3
5
4
6
