Машимов М.М. Геодезия.Теоретическая геодезия

Подождите немного. Документ загружается.

М.М.МАШИМОВ

ТЕОРЕТИЧЕСКАЯ

ГЕОДЕЗИЯ

М. М.

МАШИМОВ

ГЕОДЕЗИЯ

ТЕОРЕТИЧЕСКАЯ

ГЕОДЕЗИЯ

СПРАВОЧНОЕ ПОСОБИЕ

Под редакцией

В.П. САВИНЫХ и В.Р. ЯЩЕНКО

823245

Чершг'гаськз держмш

обмена у;-»оь»*»льи«

К-'У

"га

|м."в. Г. Королева

МОСКВА "НЕДРА" 1991

1И5К 26.1

М38

УДК 528.2/.3 (031)

„ 1802020000-035 _

043(01) -91— КВ-И-34-91 © М. М. Машимов, 1991

18ВЫ 5-247-01331-X

ПРЕДИСЛОВИЕ

В науках о Земле все более актуальными и содержательными

становятся теории решения планетарных задач. Целью настоящей кни-

ги является изложение наиболее общих и строгих теорий геодезии, знание

которых необходимо специалистам, занимающимся науками о Земле.

Разработка методов решения астрономо-геодезических задач на

базе общей теории в эру геоинформационных технологий приобрета-

ет первостепенное значение. Общая теория позволяет по одной и той

же методике обосновывать математическую модель каждой частной

задачи. Математически строго и полно решая задачу, можно выявлять

слабые и сильные элементы технологии. Совершенствование технологии,

в свою очередь, стимулирует построение математической модели более

высокого уровня и новые обобщения в теории. Ныне, как никогда,

общая теория не только дает возможность использовать дедуктивный

метод изложения, сокращающий затраты труда и времени на изучение

каждой частной проблемы, но и вооружает сильным инструментом спе-

циалиста, обосновывающего постановку и решение новой проблемы или

разрабатывающего строгое решение известной ранее задачи для удов-

летворения возрастающих запросов практики. Исходя из этой концеп-

ции, автор применил дедуктивный метод изложения общих теорий и

строгих методов решения задач геодезии.

Вторая концепция, которая определила содержание и принципы

рассмотрения теоретических задач, состоит в том, что современная

геодезия является планетарной и физической; твердая, водная и воз-

душная оболочки Земли и космос представляют единую динамическую

систему, параметры которой непрерывно изменяются во времени. Син-

тез данных астрометрии, геодезии, гравиметрии, геофизики и геодина-

мики является необходимым условием строгого решения традиционных

и новых задач планетарной геодезии.

В первых двух главах книги изложены теории систем координат,

моментов инерции Земли, методы представления геогравитационного

потенциала и изучения внутреннего строения Земли в геодезических

целях. Вопросы редукции измерений в единую систему отсчета ко-

ординат рассмотрены с применением методов координатных преобра-

зований и матричной алгебры.

Третья глава посвящена теории вращения Земли и методам изу-

чения ее динамической фигуры. Теории систем координат и гравита-

ционного потенциала, моментов инерции и динамической фигуры Земли,

механизм построения моделей гравитационного потенциала и внутрен-

него строения планетарного тела рассмотрены в общей постановке

таким образом, что они могут применяться при изучении не только

Земли, но и других планет земной группы.

В четвертой главе рассмотрена единая теория вывода строгих

уравнений наземных и спутниковых астрономо-геодезических и грави-

метрических измерений. Приложения общей теории проиллюстрированы

на примерах математического анализа всех видов измерений, включая

радиоинтерферометрические, вариометрические и гравиинерциальные

измерения.

Пятая глава освещает планетарные, региональные и геодинамиче-

ские задачи геодезии и ее связь с другими науками о Земле, вопросы

согласования геодезических и геофизических постоянных для редукции

измерений в единую систему отсчета координат и гравитации на задан-

ную эпоху. В заключение главы рассматриваются математические

принципы компьютерной обработки астрономо-геодезических и грави-

метрических измерений.

Целевую постановку задач и их описание можно легко отделить

от математических выводов, которые при чтении книги могут быть

опущены без ущерба для понимания идеи и способа решения конкрет-

ной задачи и проблемы.

Предельно ясна и бесспорна роль теории в новых геоинформаци-

онных технологиях, которые основаны на математическом анализе и

компьютерной обработке измерений. С этой точки зрения теории мето-

дов синтеза разнородных и разновременных астрономо-геодезических

и гравиметрических измерений и их совместной обработки с учетом ди-

намики макросистемы Земля — космос, подробно рассмотренные в кни-

ге, представляют интерес для широкого круга читателей, разрабатыва-

ющих и изучающих новые геоинформационные технологии на базе при-

менения ЭВМ и новых достижений наук о Земле.

I. СИСТЕМЫ ОТСЧЕТА КООРДИНАТ И ГРАВИТАЦИИ.

ОСНОВНЫЕ УРАВНЕНИЯ И РЕДУКЦИОННЫЕ ФОРМУЛЫ

1.1. ОПРЕДЕЛЕНИЯ ОСНОВНЫХ СИСТЕМ ОТСЧЕТА КООРДИНАТ

Системы координат, применяемые в современной геодезии, можно

разделить на две группы: прямолинейные прямоугольные (двухмер-

ные— на плоскости, трехмерные — в пространстве); полярные (двух-

мерные — на плоскости, на поверхности сферы или эллипсоида, трех-

мерные— в пространстве).

Система координат, начало которой находится в центре масс плане-

тарного тела или вблизи него, называется планетоцентрической или

квазипланетоцентрической. Координаты, связанные с общим земным

эллипсоидом, будут планетарными (общеземными) и геоцентрическими,

а координаты, связанные с референц-эллипсоидом,— референцными и

квазигеоцентрическими.

В планетарной геодезии применяются также гелиоцентрическая

(начало в центре масс Солнца), луноцентрическая (начало в центре

масс Луны, марсоцентрическая (начало в центре масс Марса) и

другие планетоцентрические системы координат. В отличие от плане-

тографических координат, в которых основной координатной плос-

костью является плоскость экватора соответствующего планетарного

тела (Солнца, Венеры, Марса, Луны и др.), в планетоцентрической

системе за основную координатную плоскость обычно принимается

плоскость земного экватора или другие плоскости, связанные с Землей.

В наименовании планетографических координат латинское название

небесного тела заменяется соответствующим греческим названием

(например, ареографические координаты — на Марсе, зенографиче-

ские координаты — на Юпитере).

Планетографические координаты обычно применяют для изучения

фигур небесных тел и определения положения точек на их поверхности.

Планетоцентрические координаты используют в задачах определения

фигуры Земли и положения точек земной поверхности и околоземного

пространства. В зависимости от выбранной основной координатной

плоскости различают экваториальную (экватор или плоскость, парал-

лельная экватору), эклиптическую (плоскость эклиптики), горизонтную

(плоскость местного горизонта) и орбитальную (плоскость орбиты не-

бесного объекта) системы координат.

В зависимости от выбранного направления осей координат относи-

тельно точек пространства системы координат делятся на: звездные, ес-

ли они ориентированы по далеким звездам; квазарные, если они ори-

ентированы по далеким естественным радиоисточникам (квазарам);

земные, если они ориентированы по неподвижным точкам на земной

поверхности.

Из-за прецессии и нутации оси вращения Земли, колебательных

Рис. 1. Геоцентрические экваториаль-

ные и объектоцентрические горизонт-

ные координаты

Рис. 2. Эллипсоидальные координаты

В, 1, Н относительно земного эллип-

соида с полуосями а и Ь

движений Земли относительно оси вращения и движения Земли в ми-

ровом пространстве начало отсчета, основные плоскости и оси координат

с течением времени изменяют положение и направления в пространстве.

Поэтому планетарные координаты необходимо фиксировать на эпоху,

на которую заданы параметры, изменяющиеся со временем и определяю-

щие начало и ориентирование осей координат.

В частном случае координаты, связанные с положением оси вращения

и экватора Земли на момент наблюдения, называются мгновенными или

истинными координатами.

В геоцентрической экваториальной системе оси координат задаются

относительно характерных точек земной поверхности или небесной сферы.

На рис. 1 главная ось 7. (г) направлена на Северный полюс Земли Р<>. Если

при этом ось X направить в точку С

пересечения начального меридиана

с экватором, то получим земную систему координат ХУ2, которая участ-

вует в суточном вращении Земли и неподвижна относительно точек

земной поверхности. Эта система координат удобна для определения

положения точек земной поверхности и изучения фигуры Земли.

Направляя ось х (см. рис. 1) в точку весеннего равноденствия 7,

получим звездную систему координат хуг, не связанную с суточным

вращением Земли, удобную для изучения движения небесных тел. Хотя

ее начало перемещается в мировом пространстве с некоторым ускоре-

нием, участвуя в годовом движении Земли вокруг Солнца и Солнца в

Галактике, но это движение относительно далеких звезд можно считать

равномерным и прямолинейным. Поэтому движение околоземного не-

бесного объекта в системе координат хуг можно изучать, пользуясь зако-

нами механики для инерциальной системы отсчета.

Для перехода от звездной системы отсчета координат к земной и

наоборот достаточно задать часовой угол 5 (звездное время) точки 0

на экваторе.

На рис. 1 также показаны пространственные геоцентрические поляр-

ные сферические координаты точки ф: радиус г, прямое восхождение а,

склонение б, долгота Л, широта Ф и способы их отсчета на поверхности

сферы радиуса г = 01

Положение точки <3 относительно земного эллипсоида определяелтся

геодезическими эллипсоидальными координатами: широтой В, долго-

той и высотой Н (рис. 2). Геодезической широтой точки <5 называется

острый угол Ь, образованный нормалью <Эп к поверхности эллипсоида

в данной точке и плоскостью экватора ЕО

Е'. Геодезической долготой

точки <3 называется двугранный угол, образованный плоскостью началь-

ного геодезического меридиана РО

Р' и плоскостью геодезического

меридиана Р(}оР' данной точки. Заметим, что плоскость геодезического

меридиана проходит через нормаль <2п и ось вращения эллипсоида

РОР'. Широты точек Северного полушария называются северными, они

имеют знак «+»; широты точек южного полушария — южными и име-

ют знак «—». Точки, расположенные восточнее начального меридиана,

имеют восточные долготы, а точки, расположенные западнее начального

меридиана, — западные долготы. В геодезии принято отсчитывать дол-

готы от начального меридиана против хода часовой стрелки от 0 до

360°. Отрезок нормали (2

С? называется геодезической высотой. Геодези-

ческая высота отсчитывается от поверхности земного эллипсоида в

сторону увеличения высот. Если точка расположена ниже поверхности

земного эллипсоида, то ее высоте приписывается знак «—».

От эллипсоидальных координат В, можно однозначно перейти к

координатам х, у на плоскости и обратно по соответствующим формулам,

зависящим от способа отображения поверхности эллипсоида на пло-

скости.

Системы координат пространственные прямолинейные прямоугольные

ХУ2 и эллипсоидальные ВШ, а также плоские ху составляют геодезиче-

скую систему координат.

Геодезическая система координат находит широкое применение в тео-

ретических исследованиях и практических работах в геодезии, топографии

и картографии, так как она объединяет данные геодезии, топографи-

ческих съемок и картографирования по всей поверхности Земли. Кроме

того,она определяется положением центра масс, оси вращения и эква-

тора Земли, а также нормалью к земному эллипсоиду, что весьма удоб-

но для изучения физической фигуры Земли и геоида относительно

земного эллипсоида, определения высот и решения других научных

и практических задач.

К сферическим координатам относятся астрономические широты ср

и долготы к, связанные с отвесной линией. Астрономическую широту

Ф определяют как острый угол между отвесьой линией точки <? и плос-

костью экватора Земли. Астрономическая долгота к есть двугранный

угол, образованный плоскостью начального меридиана и плоскостью

астрономического (истинного) меридиана точки ф. При этом плоскость

астрономического (истинного) меридиана содержит отвесную линию

точки (} и линию, параллельную оси вращения Земли. Правила отсчета

астрономических широт и долгот подобны правилам отсчета геодезичес-

ких широт и долгот.

Как видно из определения геодезических и астрономических широт

и долгот, между ними имеются существенные различия, которым в

геодезии уделяется большое внимание.

В мелкомасштабном картографировании и в особых условиях реше-

ния геодезических задач, где не требуется высокой точности, отличиями

геодезических и астрономических координат пренебрегают. В этом слу-

чае им дают общее название — географические координаты.

Система координат, начало которой совпадает с точкой наблюдения

на Земле (на поверхности суши, морей и океанов, под водой или под

землей), в воздушном и космическом пространстве, называется топо-

иентрической. Топоцентрические системы координат подразделяют на

экваториальную, если за основную координатную плоскость принята

плоскость, параллельная земному экватору, и горизонтную, если за

основную координатную плоскость принята плоскость горизонта

наблюдения.

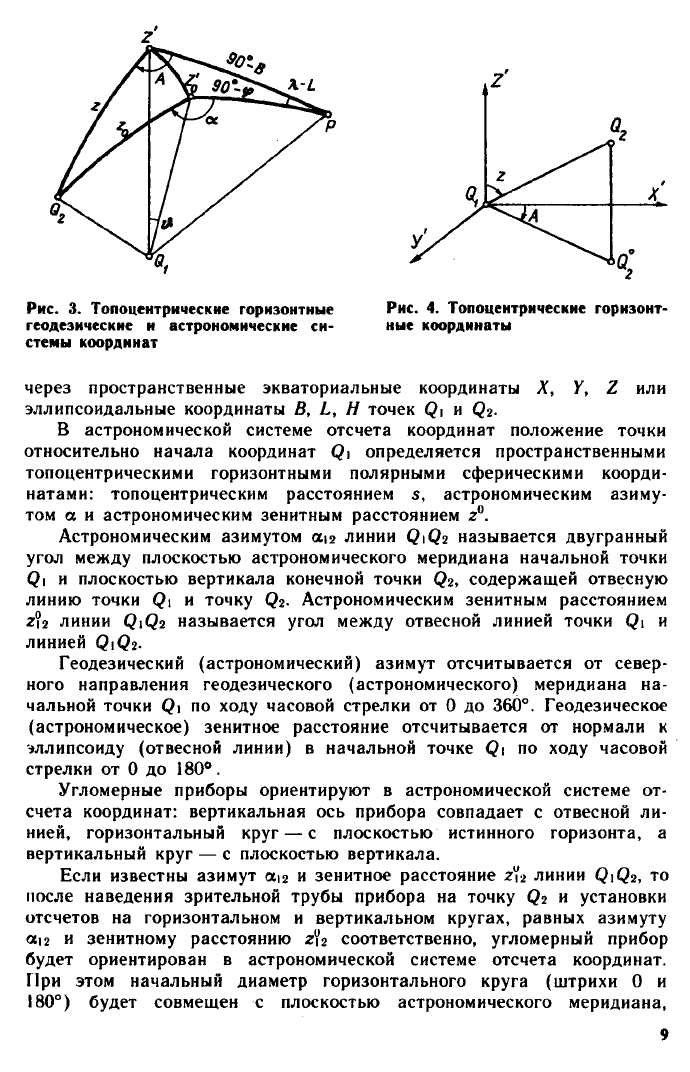
В пространственной топоцентрической горизонтной системе коор-

динат (рис. 3) если главная ось 2' совпадает с нормалью точки <2| к

земному эллипсоиду, то имеем геодезическую систему отсчета коорди-

нат; если главная ось 26 совпадает с отвесной линией точки —

астрономическую (физическую) систему отсчета координат. В первом

случае основными координатными плоскостями будут плоскости геоде-

зического горизонта и плоскость геодезического меридиана точки <2|,

а во втором случае — плоскость истинного горизонта и астрономиче-

ского (истинного) меридиана.

Пространственная топоцентрическая горизонтная геодезическая

система координат (ПТГГСК) определяется следующим образом.

Начало координат (рис. 4) совмещено с точкой ось 2' направлена

по нормали к земному эллипсоиду в сторону увеличения высот, ось X'

лежит на пересечении плоскостей геодезического горизонта и геодези-

ческого меридиана точки и направлена на север, а ось У лежит

в плоскости геодезического горизонта и дополняет левую декартову

систему координат. Положение точки С)2 относительно точки ф) опре-

деляется пространственными топоцентрическими горизонтными прямо-

угольными прямолинейными координатами Х'

У, 2' и полярными сфе-

рическими координатами: топоцентрическим расстоянием 5, геодези-

ческим азимутом А и геодезическим зенитным расстоянием г.

Геодезический азимут А12 линии ф^г есть двугранный угол между

плоскостью геодезического меридиана начальной точки и плоскостью

вертикала конечной точки <?г, содержащей нормаль точки и точку <Э

Геодезическое зенитное расстояние ги составляет угол между нормалью

точки ^^ и линией <3^2.

Топоцентрические горизонтные координаты X', У, 2', г, А, 5 точки

фг относительно начала отсчета <2| ПТГГСК однозначно определяются

г'

Рис. 3. Топоцентрические горнзонтные

геодезические и астрономические си-

стемы координат

Рис. 4. Топоцентрические горнзонт-

ные координаты

через пространственные экваториальные координаты X, У, 2 или

эллипсоидальные координаты В, Ь, Н точек и фг•

В астрономической системе отсчета координат положение точки

относительно начала координат определяется пространственными

топоцентрическими горизонтными полярными сферическими коорди-

натами: топоцентрическим расстоянием 5, астрономическим азиму-

том а и астрономическим зенитным расстоянием г°.

Астрономическим азимутом едг линии а}\()2 называется двугранный

угол между плоскостью астрономического меридиана начальной точки

и плоскостью вертикала конечной точки ($2, содержащей отвесную

линию точки и точку (?2. Астрономическим зенитным расстоянием

г°\2 линии называется угол между отвесной линией точки Р) и

линией ф^г.

Геодезический (астрономический) азимут отсчитывается от север-

ного направления геодезического (астрономического) меридиана на-

чальной точки С] по ходу часовой стрелки от 0 до 360°. Геодезическое

(астрономическое) зенитное расстояние отсчитывается от нормали к

эллипсоиду (отвесной линии) в начальной точке по ходу часовой

стрелки от 0 до 180°.

Угломерные приборы ориентируют в астрономической системе от-

счета координат: вертикальная ось прибора совпадает с отвесной ли-

нией, горизонтальный круг — с плоскостью истинного горизонта, а

вертикальный круг — с плоскостью вертикала.

Если известны азимут а\2 и зенитное расстояние г

\2 линии то

после наведения зрительной трубы прибора на точку ()2 и установки

отсчетов на горизонтальном и вертикальном кругах, равных азимуту

<Х|2 и зенитному расстоянию г°\2 соответственно, угломерный прибор

будет ориентирован в астрономической системе отсчета координат.

При этом начальный диаметр горизонтального круга (штрихи 0 и

180°) будет совмещен с плоскостью астрономического меридиана,