Martin P.M. Handbook of Deposition Technologies for Films and Coatings, Third Edition: Science, Applications and Technology

Подождите немного. Документ загружается.

Evaporation 231

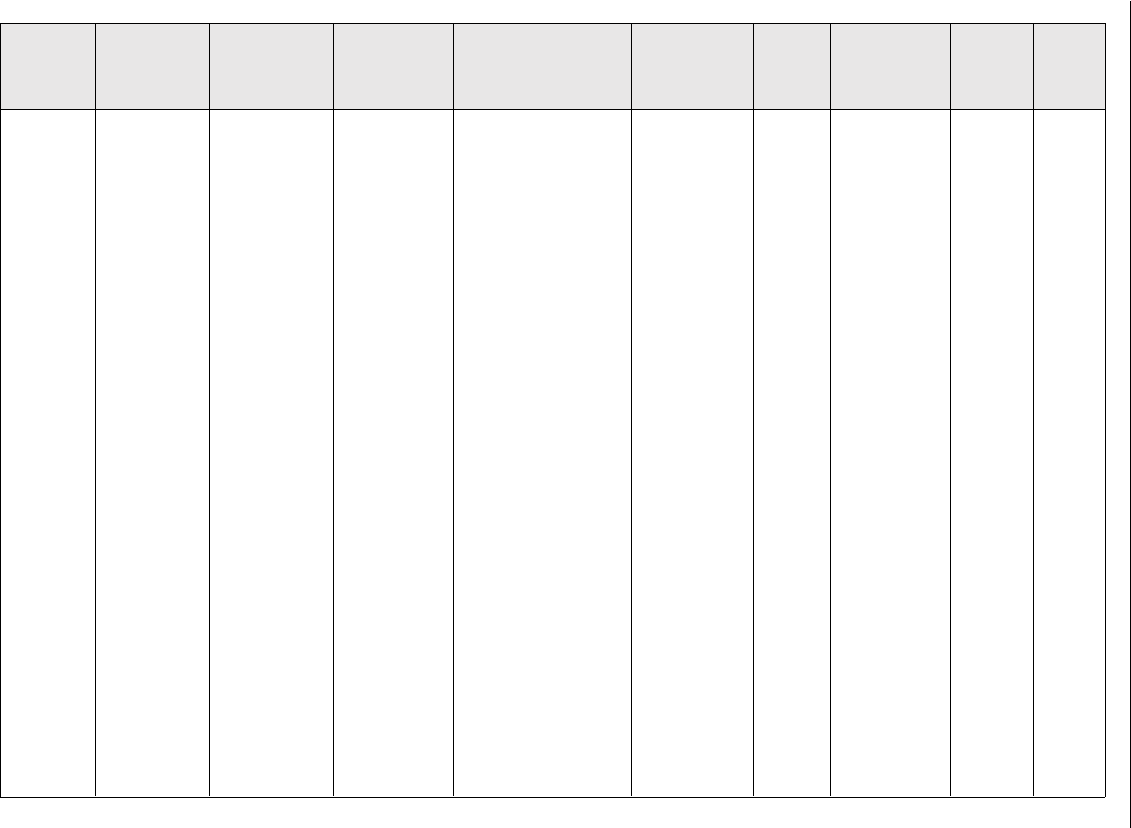
Table 4.11: Mechanical properties of thick ﬁlms or bulk condensates

Material 0.2% yield

stress

Ultimate

tensile

strength

% Elong.

(or % RA)

Microhardness

(kg/mm

)

Deposition

temp.

Grain

size

Thickness

(␮m)

Test

temp.

Ref.

(kg/mm

)(

◦

C) (␮m) (

◦

Al – – – 200 200 – 40 25 [192]

– – – 160 300 – – – –

– – – 80 400 – – – –

– – – 8 Knoop at 0.5 g

load

250–350 – 1–2 25 [182]

Cu 15 – – – – 1 4–10 25 [169]

28 – – – – 0.7 – – –

40 – – – – 0.1 – – –

45 – – – – 0.07 – – –

– 18–22 35 – 400–800 – 1000 25 [190]

– – – 240 120 – >15 25 [200]

– – – 170 180 – – – –

– 50 2.38 – – – 3–20 25 [198]

–16

(annealed

500

◦

0.27 – – – – – –

– 60 – – – 0.1 0.5 25 [31]

– 40 – – – 0.6 3–5 – –

Ag 10 – – – – 1 5–20 25 [169]

35 – – – – 0.1 – – –

Fe – 66–72 – 250 – – 20 25 [196]

45 46 4 120 400 – 1000 25 [191]

20 35 20 90 550 – – – –

15 25 18 75 700 – – – –

Be – 140 0.1 240 (Knoop) 350–425 – 75–100 25 [188]

– 281 0.3 215 480–550 – – – –

(Continued)

232 Chapter 4

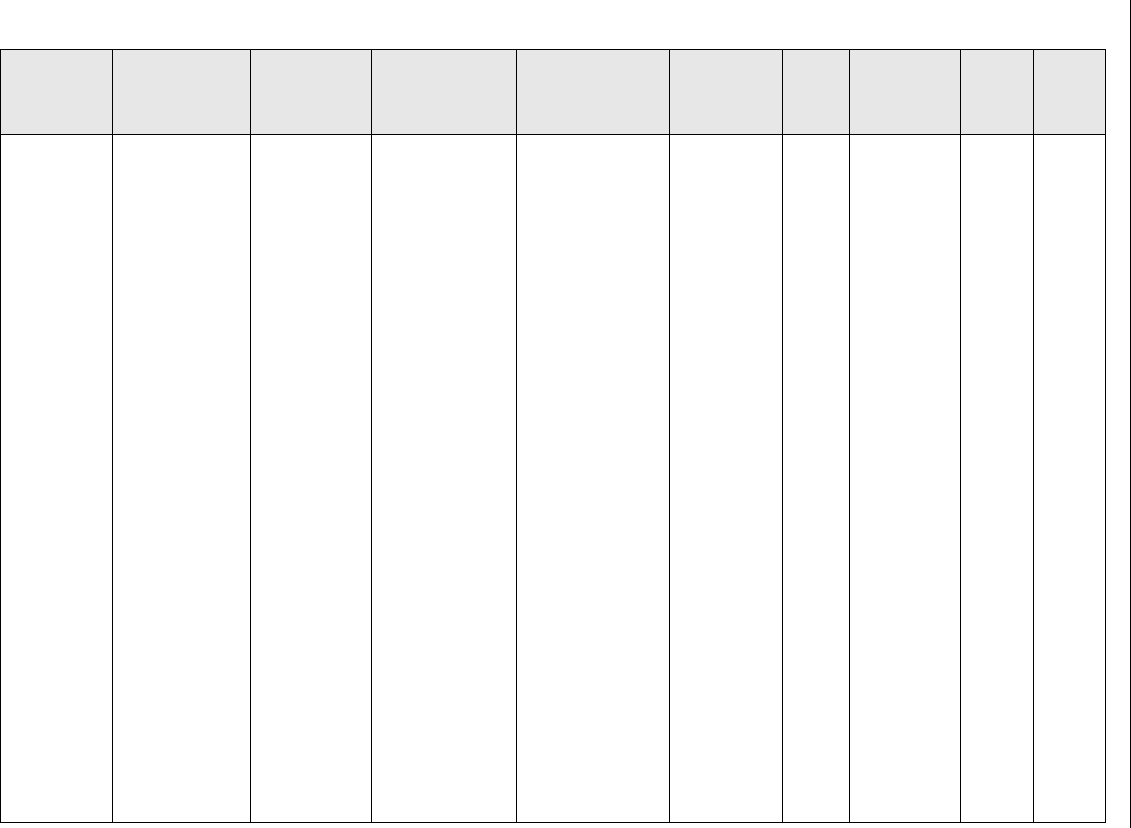
Table 4.11: (Continued)

Material 0.2% yield

stress

Ultimate

tensile

strength

% Elong.

(or % RA)

Microhardness

(kg/mm

)

Deposition

temp.

Grain

size

Thickness

(␮m)

Test

temp.

Ref.

(kg/mm

)(

◦

C) (␮m) (

◦

– 316 0.45 168 625–685 – – – –

– 295 1.0 170 760–790 – – – –

62 (bend

test)

– > 4 (bend

test)

– – 100 1000 25 [18]

47 (bend

test)

– > 5.2 (bend

test)

––––––

Ni – 115 0.3 – – 0.2 0.2–2 25 [191]

– 66–74 – 250 400–420 – 20 25 [199]

– – – 450 260 – – – –

– – – 600 220 – – – –

129 338 39 (20) 96.6 554 26 275 25 [113]

135 336 32 (20) 109 245 19 375 – –

155 366 35 (21) 104 329 12.7 375 – –

247 403 21 (21) 125 260 3.7 375 – –

140

(melted

and

wrought)

407 44 (30) 91 – 18 357 – –

– 138 0.6 – – – 2.6 25 [142]

– – – – 250 620 1000 25 [97]

– – – – 400 420 – – –

– – – – 600 380 – – –

– 28 20 – 400 – 1000 25 [190]

– 38 12 – 800 – – – –

Ti 189 295 25 (66) – 800 32 250 25 [112]

225 302 20 (38) – 600 8 250 25 –

Evaporation 233

Table 4.11: (Continued)

Material 0.2% yield

stress

Ultimate

tensile

strength

% Elong.

(or % RA)

Microhardness

(kg/mm

)

Deposition

temp.

Grain

size

Thickness

(␮m)

Test

temp.

Ref.

(kg/mm

)(

◦

C) (␮m) (

◦

436 471 3 (25) – 450 1 250 25 –

189

(melted

and

wrought)

302 40 (61) – – 50 250 25 –

– – – 560 200 – 1000 25 [97]

– – – 200 400 – – – –

– – – 130 500 – – – –

280–420 – 20 – – – 100–250 25 [134]

140–280 – 35 – – – – 200 –

Mo 14 19 (5.3) 191 990 530 300 – [186]

24 28 (0.8) 169 704 85 – – –

38 44 (1.0) 186 804 19 – – –

Nb 19 – 7.3 112 745 10 300 – [186]

V 37 – 22 115 540 0.7 300 – [186]

W – – – 720 600 – 1000 25 [97]

– – – 460 1000 – 1000 25 –

– – – 300 1000 – 1000 25 –

Ni–20Cr 337 540 26 (27) 80 950 13 375 25 [189]

577 780 21 (26) 112 780 2.6 375 25 –

752 871 18 (19) 131 680 1.8 375 25 –

1195 1223 6 (8) 180 427 0.5 375 25 –

393

(melted

and

wrought)

569 37 (31) 78 – 10.4 325 25 –

25 49 25 (21) – 950 13 375 1000 –

234 Chapter 4

Table 4.11: (Continued)

Material 0.2% yield

stress

Ultimate

tensile

strength

% Elong.

(or % RA)

Microhardness

(kg/mm

)

Deposition

temp.

Grain

size

Thickness

(␮m)

Test

temp.

Ref.

(kg/mm

)(

◦

C) (␮m) (

◦

40.9 60 53 (41) – 680 1.8 375 1000 –

Ti–6Al–4V 970–1195 1068–1195 1–12 – – – 79 25 [32]

80Ni–20Cu – 35–45 8–25 – 400–800 – 375 1000 [190]

50Ni–50Cu – 40–55 5–20 – 400–800 – 375 1000 –

20Ni–80Cu – 27–42 10–30 – 400–800 – 375 1000 –

80Ni–16Fe – 180 – 650 200 – – 25 [200]

(permalloy) 150 – 250 400 – – 25 –

– – – 380 400 – 300 25 [97]

– – – 80 600 – 300 25 –

– – – 200 1000 – 300 25 –

– – – 1000 1400 – 300 25 –

– – – 500–800 1100 – 300 25 [202]

ZrO

– – – 450 400 – 300 25 [97]

– – – 350 600 – 300 25 –

– – – 400 1000 – 300 25 –

– – – 1000 1400 – 300 – –

– 248 – 384 120 3.2 100 25 [203]

– 226 – 256 210 5 100 25 –

– 215 – 331 304 8 100 25 –

– 208 – 320 416 14 100 25 –

– 205 – 360 538 21 100 25 –

– 198 – 502 721 58 100 25 –

O – – – 960–1960 750 – – 25 [102]

TiO – – – 700–2015 1100 – – 25 –

SiO

– – – 300 – – 10 25 [203]

C – – – 1907–2440 500 – – 25 [197]

Evaporation 235

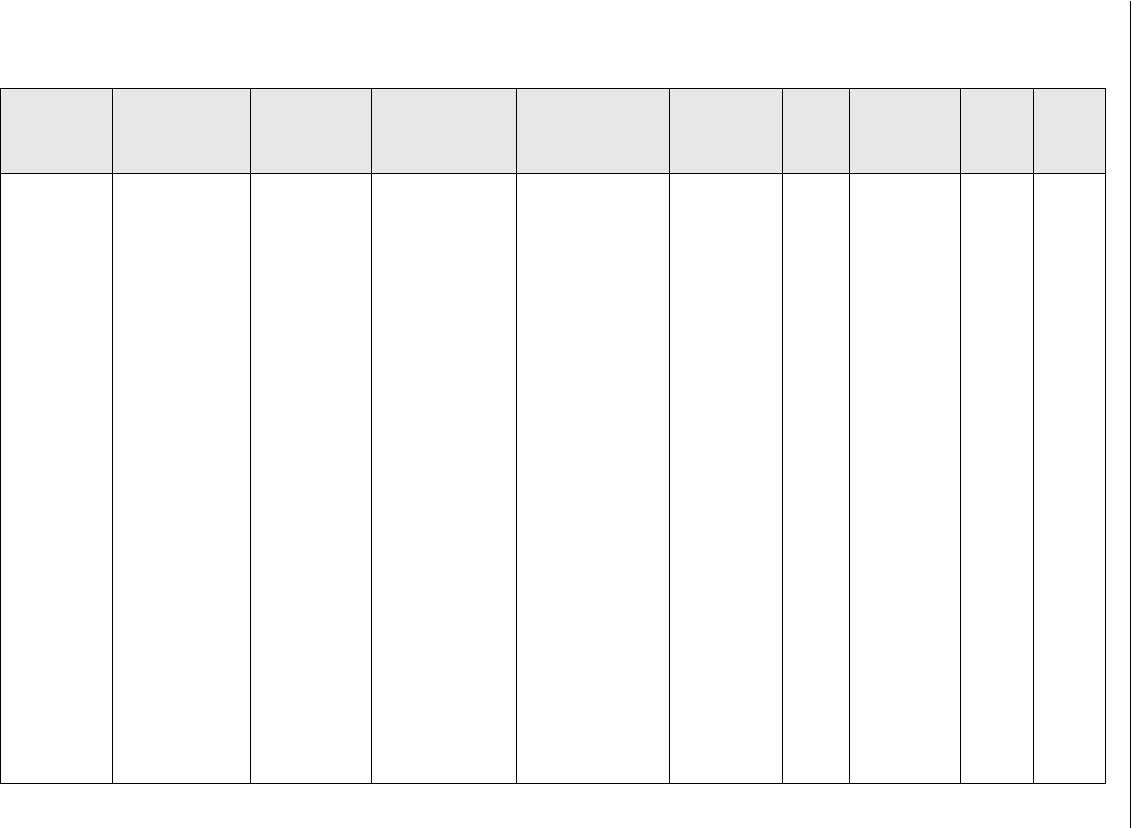
Table 4.11: (Continued)

Material 0.2% yield

stress

Ultimate

tensile

strength

% Elong.

(or % RA)

Microhardness

(kg/mm

)

Deposition

temp.

Grain

size

Thickness

(␮m)

Test

temp.

Ref.

(kg/mm

)(

◦

C) (␮m) (

◦

TaC – – – 1800–2400 500 – – 25 –

SiC (RF

sputter)

– – – 3500–4000 – – 2.6 25 [205]

TiC (ARE

process)

– – – 2710 520 – 50 25 [116]

– – – 2955 730 – 50 25 –

– – – 2955 830 – 50 25 –

– – – 4110 1080 – 50 25 –

– – – 4160 1120 – 50 25 –

– – – 2400 – – 5 25 [206]

ZrC – – – 2500–2800 550 – 50–75 – [101]

(Hf–3Zr)C – – – 2700–3030 550 – 50–75 – –

VC – – – 2350 550 – 50–75 – [101]

NbC – – – 2300 550 – 50–75 – –

Laminates

Cu–Ni

laminate

– 35–55 13 – – – 2 25 [207]

Cu–Fe

laminate

35–70 110 – 400–800 240–360 – 15–25 25 [208]

Cu–Ni

laminate

– 80 1.8 – 300 – 0.1 25 [209]

Cu–Fe

laminate

– 125 0.88 – 150 – 0.04 25 –

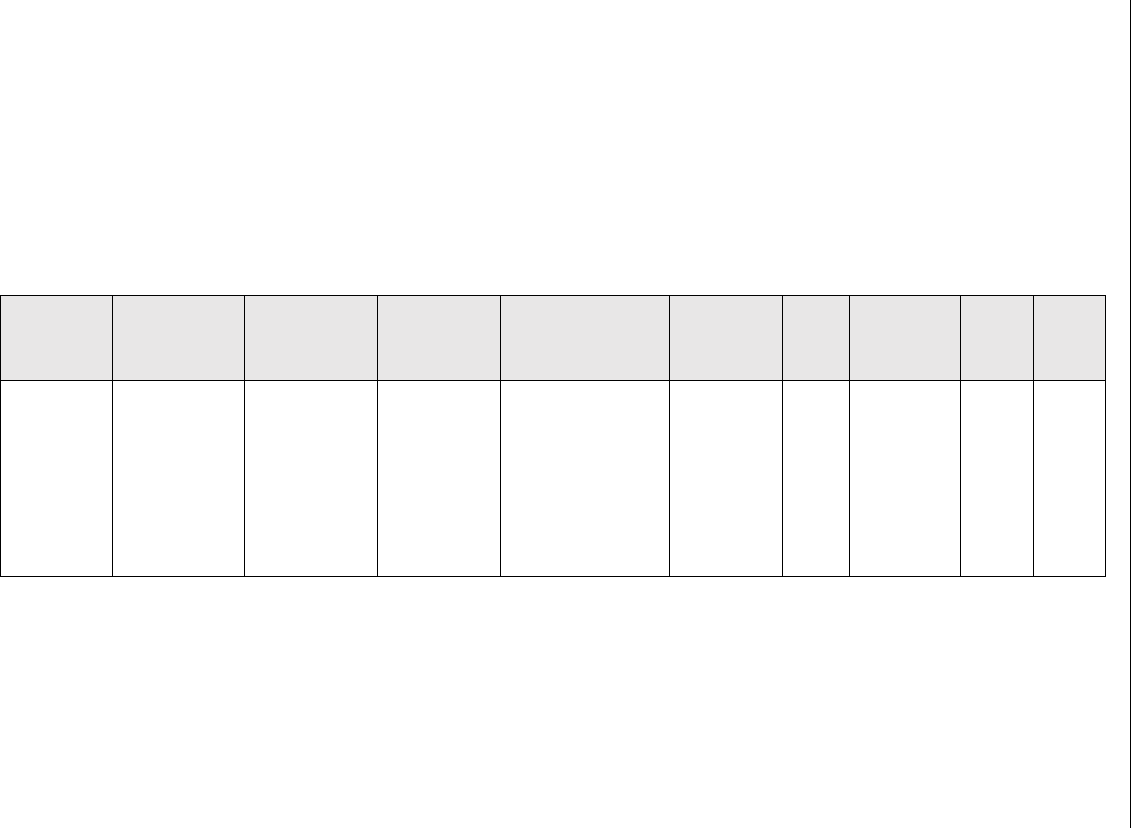
236 Chapter 4

Table 4.11: (Continued)

Material

0.2% yield

stress

Ultimate

tensile

strength

% Elong.

(or % RA)

Microhardness

(kg/mm

)

Deposition

temp.

Grain

size

Thickness

(␮m)

Test

temp.

Ref.

(kg/mm

)(

◦

C) (␮m) (

◦

Ni–Fe

laminate

– 150 0.45 – 150 – 0.04 25 –

Ni–SiO – 150 – 300 – – 20 25 [217]

– 105 – 300 – – 20 200 –

– 95 – 300 – – 20 400 –

– 80 – 200 – – 20 600 –

Ti–TiC – 251 1.8 – 500 – 250 – [211]

Evaporation 237

We consider each type of material separately since the behavior of metals and alloys is vastly

different from that of refractory compounds.

The early work in this area was that of Bunshah [17, 18], Bunshah and Juntz [22], and Smith

[23], who deposited thick ﬁlms of Be, Ti, and Cu, respectively, and measured mechanical

properties. In 1965, Palatnik et al. published a paper on mechanical properties of Al

condensates [240]. It is impossible to review in detail all the papers. The pertinent data are

shown in Table 4.11 and the discussion below concentrates on the highlights.

4.11.1.4 Tensile Properties and Hardness of Metal and Alloy Deposits

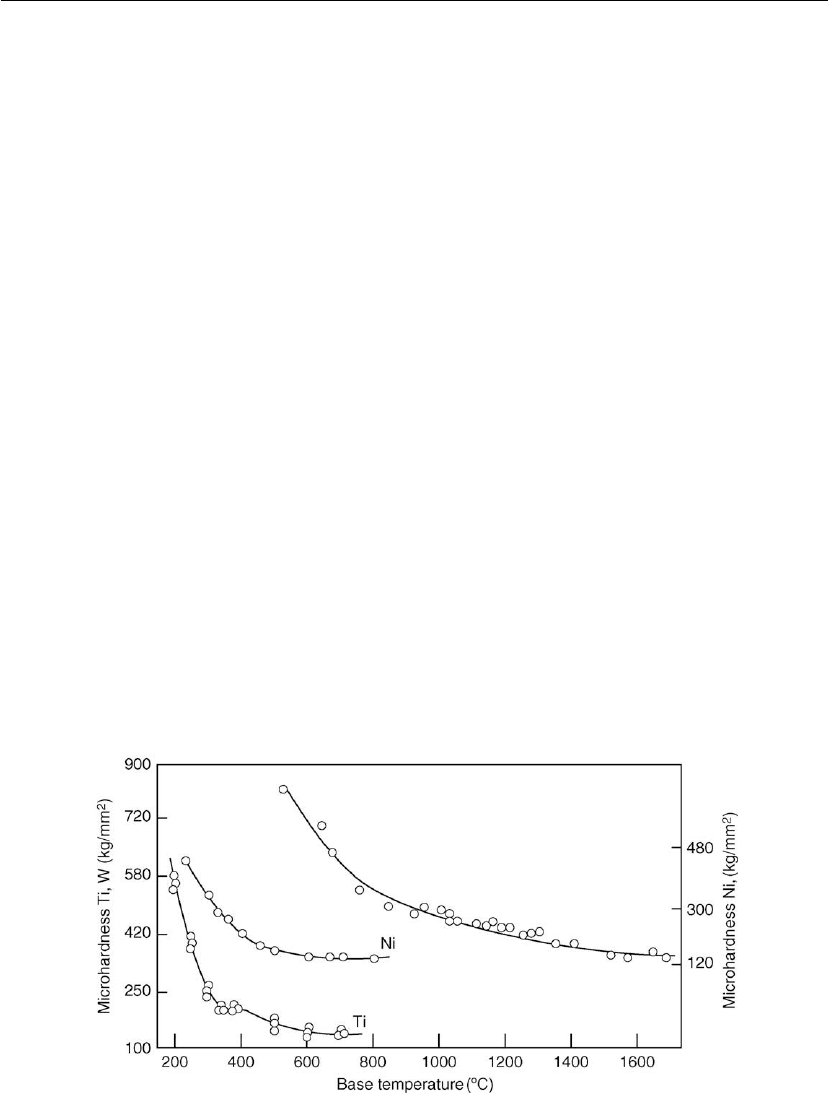
Movchan and Demchishin [123] studied the tensile properties and microhardness of Ni, Ti,

and W condensates produced at various deposition temperatures. No tensile tests were

performed on specimens deposited in zone 1 (Figure 4.62). Tests on specimens deposited in

zone 2 showed high strength and low ductility at low deposition temperature. The strength

decreased and the ductility increased with deposition temperature. The strength and ductility

values of specimens deposited in zone 3 showed approximately the same values as for

recrystallized specimens produced from wrought material. The microhardness variation with

deposition temperature for Ni, Ti, and W is shown in Figure 4.64. The tapered crystallite

morphology in zone 1 showed a high hardness much greater than that of annealed metal. The

hardness decreased rapidly with increasing deposition temperature to a fairly constant value

for zone 3 morphology, which corresponds to the hardness of recrystallized metals.

Bunshah and co-workers studied the effect of deposition temperature on the grain size, tensile

properties, and hardness of Ti [22, 196],Ni[198], Nb, V, Mo [185], and Ni–20Cr [194] alloys

for deposits made in zones 2 and 3. They found that increasing deposition temperature

produced larger grain size, lower strength, higher ductility, and lower hardness. Even at the

Figure 4.64: Variation of microhardness with deposition temperature of metals.

238 Chapter 4

lowest deposition temperature in zone 2, the ductility was good (> 20% RA for 1 ␮m grain

diameter Ti at a yield strength of 56,000 psi). Moreover, they found that both the yield strength

and hardness varied as the inverse square root of grain diameter, i.e. followed the Hall–Petch

relationship [249, 250], which is

= σ

+ kd

−

(4.12)

where σ

is the yield strength, d is the grain diameter, and σ

and k are constants. Figure 4.65

shows an example of this relationship for Ni–20Cr alloy.

For all these metals and alloys, the yield strength, ductility and hardness values correspond to

those of the same materials produced by casting, mechanical working, and recrystallization.

The variation of yield strength and hardness with grain size, i.e. Hall–Petch type relationships,

were also very similar between the deposited and wrought materials, small variations being

Figure 4.65: Yield stress vs inverse square root of average diameter for Ni–20Cr alloy at 25



C. :

wrought; O: deposited; : Wilcox et al.;



: Webster ([251], Ref s 12 and 13).

Evaporation 239

ascribable to differences in grain morphology and preferred orientations. The Ni–20Cr alloy

showed good strength at 1000

◦

C and also obeyed the Hall–Petch relationship.

The Hall–Petch relationship is also obeyed by thick ﬁlms of Cu and Ag to grain sizes as small

as 0.05 ␮m, as shown by Nenioto et al. [252]. Thus, these thick deposits behave as true

engineering materials.

Chambers and Bower [253] studied the mechanical properties of 18-8 stainless steel, gold, and

magnesium, and showed that their tensile properties were very similar to their wrought

counterparts.

Smith et al. [27] studied the (α + β) type Ti–6Al–4V alloy. They showed that the tensile

properties are very similar to the wrought material except for a much smaller value in

percentage elongation due to premature onset of plastic instability in a tensile test at pinholes

in the deposited samples. The bend ductility was, however, superior to the wrought material.

Shevakin et al. [120] studied the strength and hardness of aluminum and copper condensates as

a function of the deposition parameters. They found that the mechanical properties varied

widely with changes in process parameters. The deposited materials also showed higher

strength and plasticity than the same materials conventionally fabricated, i.e. casting followed

by the neomechanical treatments. They also found that the hardness values obeyed the

Hall–Petch relationships.

Paton et al. [31] showed that it is possible to produce thick deposits of all the alloys across the

Cu–Ni system and that the mechanical properties vary systematically with composition, as

would be expected.

Dispersion-strengthened alloy deposits

The ﬁrst data on dispersion-strengthened alloys produced by evaporation methods were

reported by Paton et al. [31], who showed that Ni–ZrO

alloys produced by co-evaporation

from two sources contained ZrO

particles in the size range of 150–3000

A by changing the

deposition temperature from 650 to 1100

◦

C. They also showed that the creep strength at

1000

◦

C increased with volume fraction of zirconia. These alloys showed remarkable stability

in the microstructure and mechanical properties even after creep exposures of 5 h at 1300

◦

Subsequently, Movchan et al. studied the structure and properties of Ni–ZrO

alloys [183], and

Fe with Al

, ZrO

, ZrB

,TiB

, NbC, or TiC second phases [254]. The alloys were produced

by co-evaporation of the constituents from e-beam-heated evaporation sources.

One of the very striking effects of the incorporation of a dispersed phase in an evaporated

metallic coating is a very pronounced reﬁnement in grain size, often by a factor of 10–100, or

more, and the inhibition of grain growth at elevated temperatures. This was ﬁrst reported by

Kennedy [203] for the incorporation of Y

dispersions in Fe condensates. It was also

observed by Majumder [207] for Cu–Al

deposits and by Jacobson et al. [256] in Ni–Al

240 Chapter 4

deposits. In a very recent paper, Movchan and Demchishin [123] show the grain size reduction

in the Ni–Al

, Fe–ZrO

, Fe–ZrB

, and Fe–NbC deposits. The most intense grain reﬁning

effect is observed at low volume fractions (0.5 vol.%) of the second phase.

Of particular interest to this topic is a subsequent paper by Majumder [257] showing the strong

effect of alumina content in increasing creep strength, which conﬁrms the model proposed by

Mott [258], who suggested that the ideal creep-resistant material is one with a ﬁne grain size in

which the grain boundaries are ﬁlled with some substance, say a refractory oxide, to inhibit the

motion of grain boundaries.

Perhaps the most interesting result from Movchan’s work [181, 254, 259] is that the dispersed

phase alloys show a maximum in room temperature ductility in the W–ZrO

system at 1 vol.%

ZrO

, in the Fe–Al

system at 0.3 vol.% Al

, and in the Fe–NbC system at 0.1 vol.%

NbC. The yield strength and tensile strength do not show such a maximum but monotonically

increase with volume fraction of the oxide phase. The signiﬁcance of this observation lies in

the possibility of increasing the ductility of MCrAlY coatings which, in turn, would result in

increased resistance to spalling, thermal shock, and fracture, thus improving the performance

of the coating. One might speculate on reasons for this effect, including strain–relaxation sites

at particle matrix interface, or at grain boundaries owing to the greatly increased grain

boundary area, favorable changes in residual stress distribution in the coating possibly due to

changes in elastic modulus or strength, increased toughness or crack propagation resistance

conferred by the dispersed phase particles, change in crystallographic texture, etc.

Movchan et al. [260] recently presented a very detailed treatment on the regulation of

microstructure and mechanical properties of thick vacuum condensates with the help of

dispersed phases. They give a detailed theoretical model of (1) the inﬂuence of dispersed

phases on grain size; (2) the size and shape of dispersed particles as affected by deposition

parameters; (3) strength and ductility of two-phase condensates as inﬂuenced by the grain size,

particle size, mean free path, nature of the particle (deformable vs non-deformable) and

particle-matrix adhesion energies; and (4) steady-state creep behavior. The model is then

conﬁrmed by the experimental results. As a good illustration of one of these points, Movchan

[206] studied the difference in strength and ductility versus volume fraction of second phase

when the latter is deformable or non-deformable. For both types of particles, there is a

ductility maximum at a particular D

/L ratio, but the strength behavior is diametrically

opposite, showing a monotonic increase for a non-deformable particle and a minimum for the

deformable particle. D

is the grain size in the plane perpendicular to the vapor ﬂux direction

and L is the interparticle spacing. This model forms an excellent basis for design of

experiments to study the effect of dispersed phases on the structure and properties of MCrAlY

alloys.

Another fascinating observation by Movchan et al. [260] applies to two-phase alloys with

deformable particles having a high adhesion to the matrix. The ductility of the alloys exceeds