Мархель И.И. Детали машин
Подождите немного. Документ загружается.

при равных условиях. В зацеплении Новикова контакт зубьев теоретически осуществляется в точке, в
эвольвентном зацеплении соприкосновение зубьев происходит по линии. Однако при одинаковых габаритных
размерах передачи соприкосновение зубьев в зацеплении Новикова значительно лучше, чем соприкосновение в
эвольвентном зацеплении.
Какие профили зубьев имеют распространенное применение в машиностроении? Основное конструктивное
отличие зуба Новикова от известных.
3.83. Достоинства и недостатки передач с зацеплением Новикова. Высокая нагрузочная способность
является основным достоинством передач с зацеплением Новикова. При твердости рабочих поверхностей до
НВ 350 можно принимать допускаемую нагрузку примерно в 2,5 раза больше допускаемой нагрузки для
эвольвентных прямозубых передач тех же основных размеров, выполненных из тех же материалов, с той же
термической обработкой (сравнение допускаемых нагрузок произведено при коэффициенте нагрузки К= 1).
Благодаря большей нагрузочной способности передачи с зацеплением Новикова более компактны, имеют
почти в 2 раза меньшие габариты по сравнению с передачами с эвольвентным зацеплением при одинаковой пе -
редаваемой мощности.
Передачи с зацеплением Новикова допускают большее передаточное число, а вследствие хорошо
удерживающейся масляной пленки между соприкасающимися зубьями уменьшается изнашивание зубьев,
повышается КПД передачи.
Потери на трение в зацеплении Новикова примерно в 2 раза меньше, чем потери в эвольвентном
зацеплении. Шум во время их работы значительно ниже.
Недостатками являются:
• большая (чем в эвольвентных зацеплениях) чувствительность к изменению межосевого расстояния;
• с увеличением нагрузки в зацеплении возрастает осевая составляющая, что, в свою очередь, усложняет
конструкцию применяемых подшипниковых узлов;
• при ухудшении контакта (например, в случае перекоса валов и изменения межосевого расстояния) вся
нагрузка, действующая на зубья, может сосредоточиться на небольшом участке длины зубьев, в результате
чего зубья могут оказаться сильно перегруженными;
• необходимость иметь две специальные фрезы для нарезания зубьев (для шестерни и колеса).
Перечислите недостатки и основные достоинства зубчатых передач с зацеплением Новикова и запишите в
конспект.
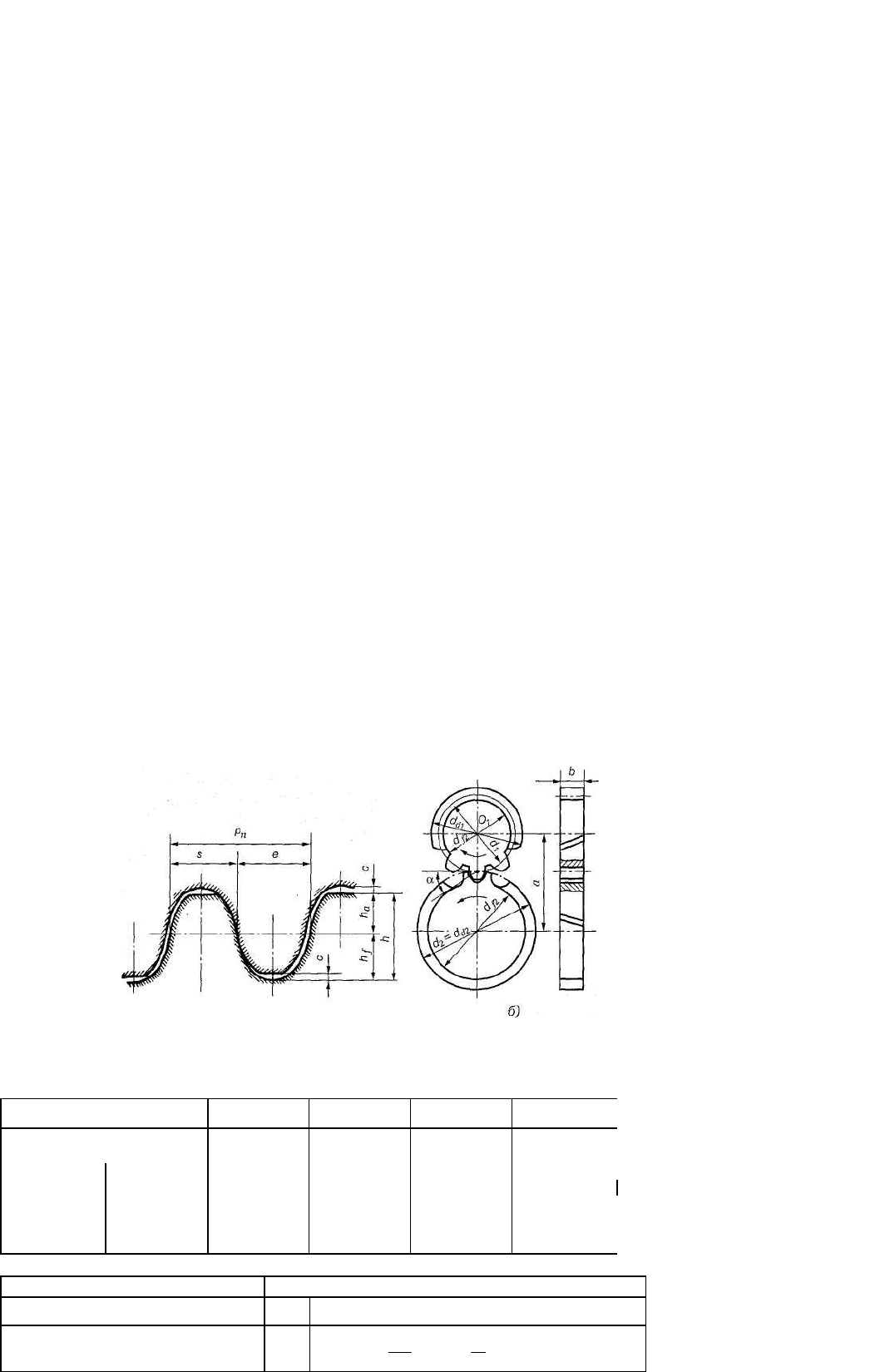
3.84. Стандартные исходные контуры для цилиндрической зубчатой передачи с зацеплением Новикова
для выпуклых (шестерня) и вогнутых (колесо) зубьев (рис. 3.59, а).
Основные геометрические размеры этих передач (рис. 3.59, б) определяют в зависимости от значения
нормального модуля т
п
(табл. 3.16 и 3.17).
а)
Рис. 3.59. Косозубая передача с зацеплением М. Л. Новикова
Таблица 3.16. Стандартные значения модулей для передачи с зацеплением Новикова
1-й ряд
2-й ряд
1-й ряд 2-й ряд 1-й ряд 2-й ряд
1,6 6,3 25
2,0
1,8
8
7,1
28
2,5
2,25
10
9
31,5
35,5
3,15
2,8
12,5
П,2
40
45
4
3,55
16
14
50
56
5
4,5
20
18
63
5,6 22,4
i
Таблица 3.17.
Геометрические
параметры
передачи с зацеплением Новикова
Параметр, обозначение Расчетные формулы
Нормальный модуль т„
; cos ; cos
n
n n n t
p
d
m m m m
z
Торцовый модуль т
t
; ;
cos
t n
t t t
p m
d
m m m
z
Диаметр вершин зубьев d
a
d
a
= m
t
z + 1,8m
n
Делительный диаметр d d = m
t
z
Основной диаметр d
b
d
b
= m,z cos α
Диаметр впадин зубьев df d, = m,z - 2,1 т„
Нормальный шаг р„ р„ = πт„
Торцовый шаг р
t
P
t
= πm
t
Осевой шаг р
х
sin
n
x
m
p
Окружная толщина зубьев 5 s = 1,53m
n
Окружная ширина впадин зубьев
е
e = 1,6m
n
Высота зуба h h = 1,95m
n
Высота головки зуба h
a
h
a
= 0,9m
n
Окончание табл. 3.17
Параметр, обозначение Расчетные формулы
Высота головки зуба h
f
h
f
= 1,05m
n
Радиальный зазор с
с = 0,15m
n
Ширина венца b
b = kp
x
+ ∆b
Межосевое расстояние а
ω
2cos 2
n t
m z m z
a
Примечание, β— угол наклона зубьев; β = 10 ÷ 30°; k — целое число осевых шагов р
х
в ширине венца; ∆b — часть ширины венца
больше целого числа осевых шагов (ширину венца рекомендуется выбирать с учетом выполнения условия b> 1,25р
x
.); Z
∑
= Z\ + Z2 —
суммарное число зубьев.
Запишите в конспект формулы для определения геометрических параметров передачи с
зацеплением Новикова (табл. 3.16). Выведите формулу межосевого расстояния а, если известны d
2
и и,
(u запишите ее в конспект).
§ 20. Расчет передачи с зацеплением Новикова на контактную прочность
3.85. Этот расчет производят по аналогичным расчетным формулам на контактную прочность для
косых зубьев эвольвентного зацепления {см. шаги 3.60, 3.61), но с учетом их большей нагрузочной
способности. На основании опытных данных несущую способность зубьев зацепления Новикова по
контактной прочности принимают в 1,75—2 раза больше, чем для эволь-вентных зацеплений.
Вспомните формулы расчета на контактную прочность цилиндрической эвольвентной прямозубой передачи.
3.86. Условия контакта в передачах с зацеплением Новикова отличаются от условий контакта по Герцу
(малая разность r
1
и r
2
большие значения ρ
1
и ρ
2
). Контактные напряжения приближаются к напряжениям
смятия. Расчет передач Новикова по контактным напряжениям применяют условно и ведут аналогично расчету
с эвольвентным зацеплением.
Для зацепления Новикова коэффициент К
а
= 33,6 МПа
|/3
, а при расчете эвольвентной передачи К
а
= 49,5 ÷
43 МПа'
/3
. Это объясняется тем, что несущая способность зубьев с зацеплением Новикова в 1,75—2 раза
больше по сравнению с эвольвентными передачами.
Ширина колеса не влияет на прочность зубьев на излом при зацеплении Новикова. В передачах с
зацеплением Новикова нагрузка, распределенная на площадке контакта, приложена не по всей длине зуба, как
это имеет место в эвольвентном зацеплении, а лишь на сравнительно небольшом его участке. При этом
значительная часть зуба практически ее не воспринимает. Следовательно, изменение ширины венца колеса b
при неизменном угле наклона зуба в отличие от эвольвентных колес практически не сказывается на прочности
зубьев на излом.
§ 21. Планетарные зубчатые передачи. Устройство передачи и расчет на прочность
3.87. Передачи, имеющие зубчатые или фрикционные колеса с перемещаю-щимися осями, называют
планетарными.
Наиболее распространена зубчатая однорядная планетарная передача (рис. 3.60). Она состоит из
центрального колеса / с наружными зубьями, неподвижного (центрального) колеса 2 с внутренними
зубьями и водила -на котором закреплены оси планетарных колес g (или сателлитов).

Рис. 3.60. Планетарная передача
Водило вместе с сателлитами вращается вокруг центральной оси, а сателлиты обкатываются по
центральным колесам и вращаются вокруг своих осей, совершая движения, подобные движению планет.
При неподвижном колесе 2 движение передается от колеса 1 к водилу h или наоборот.
Планетарную передачу, совершаемую подвижными звеньями (оба иен-тральных колеса и водило),
называют дифференциалом. С помощью дифференциала одно движение можно разложить на два или
два движения сложить в одно: от колеса 2 движение можно передавать одновременно колесу 1 и водилу
h или от колес 1 и 2 к водилу /г и т. д. Планетарную передачу успешно применяют в транспортном
машиностроении, станкостроении, приборостроении.
Какие профили зубьев применимы для планетарной зубчатой передачи?
3.88. Достоинства и недостатки планетарных передач.
Основное достоинство — широкие кинематические возможности, позволяющие использовать
передачу в качестве редуктора коробки скоростей, передаточное число в которой изменяется путем
поочередного торможения различных звеньев, и как дифференциальный механизм.
Планетарный принцип позволяет получать большие передаточные числа (до тысячи и больше) без
применения многоступенчатых передач.
Эти передачи компактные и имеют малую массу. Переход от простых передач к планетарным
позволяет во многих случаях снизить их массу в 4 раза и более.
Сателлиты в планетарной передаче расположены симметрично, а это снижает нагрузки на опоры
(силы в передаче взаимно уравновешиваются), что приводит к снижению потерь и упрощает
конструкцию опор.
Эти передачи работают с меньшим шумом, чем обычные зубчатые.
Основные недостатки: повышенные требования к точности изготовления и монтажа; резкое
снижение КПД передачи с увеличением передаточного отношения.
Перечислите примеры возможного применения планетарных передач.
3.89. Передаточное отношение.
Для определения передаточного отношения планетарной передачи используется метод Виллиса —
метод останова водила.
Передаточное отношение планетарной передачи (см. рис. 3.60)
1 2 1 2 1 2
( ) / /
h h
i z z
(3.33)
где
1
( )
h
и
2 h
— угловые скорости колес 1 и 2 относительно водила h; Zi и z
2
— числа
зубьев этих колес.
Для реальной планетарной передачи (колесо 2 закреплено неподвижно, колесо 1 — ведущее, водило
h ведомое) при ω
2
= 0 из формулы (3.36) получим
1 1 2 1 1 2
( ) / / ; / 1 /
h h h
z z z z
или
1 1 1 2
/ 1 /
h h
i z z
(3.34)
Для однорядной планетарной передачи I = 1,25 ÷ 8,0 для многоступенчатых i=30 ÷ 1000, для
кинематических передач i
1h
≥ 1600. Чем больше передаточное отношение планетарной передачи,
тем меньше КПД
(
л
= 0,99 ÷ 0,1).
3.90. Расчет на контактную прочность зубьев планетарных передач проводится по аналогии с
расчетом обыкновенных зубчатых передач отдельно для каждого зацепления (см. рис. 3.60): пара колес
1—g (внешнее зацепление) и g—2 — (внутреннее). Для таких передач достаточно рассчитать-только
внешнее зацепление, так как модули и силы в зацеплениях одинаковые, а внутреннее зацепление
прочнее внешнего.
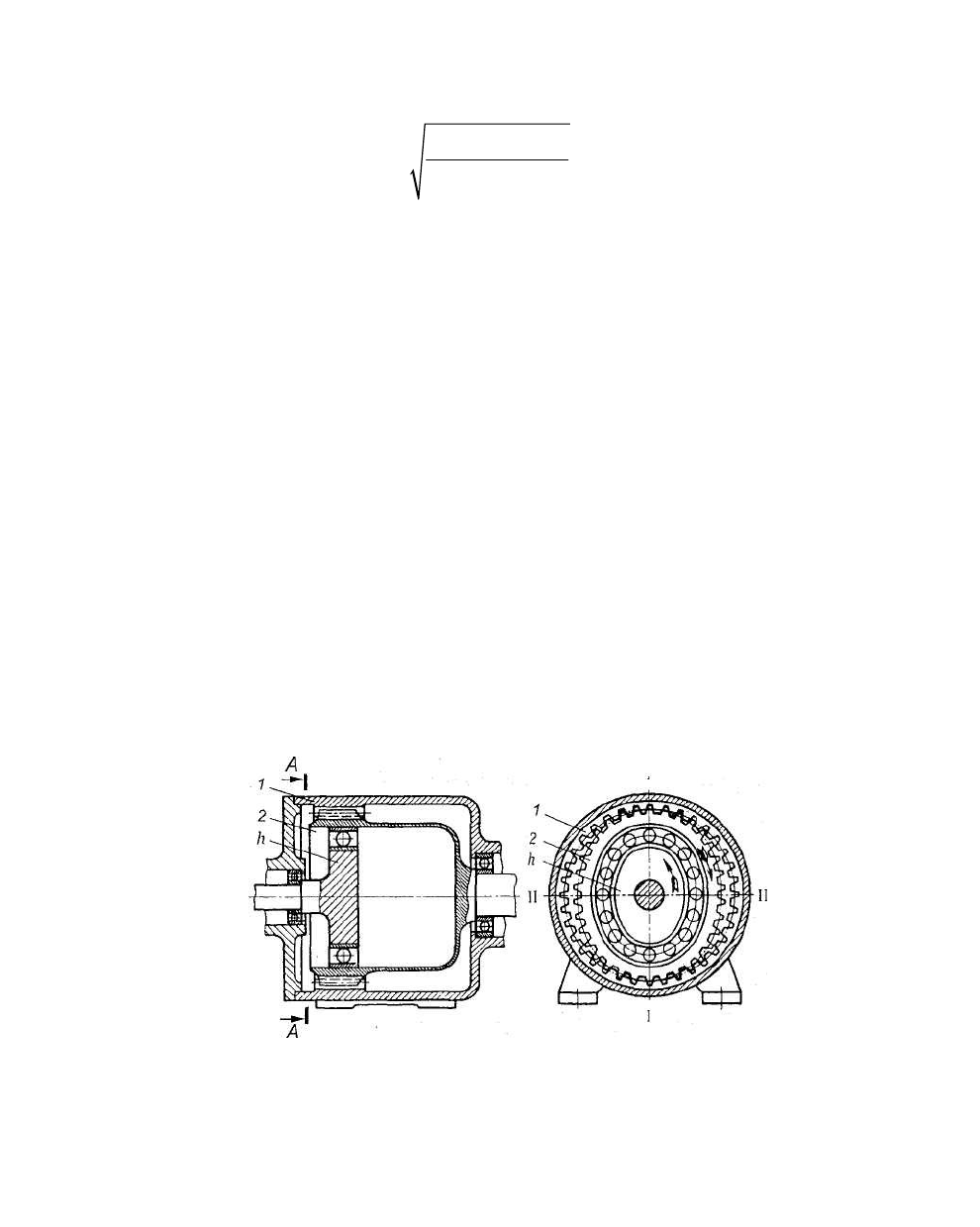
Объясните, почему для планетарной передачи (см. рис. 3.60) достаточно рассчитать только внешнее
зацепление.
3.91. Проектировочный расчет планетарной передачи на контактную усталость активных
поверхностей зубьев проводится по следующей формуле:
2 1 2
3
1
2
1 2
1
H
d
bd
i
H
T K i
d K
i
(3.35)
где d
t
— делительный диаметр ведущего звена (шестерни), мм; K
d
= 78 МПа
1/3
— вспомогательный
коэффициент (рассматриваются стальные прямозубые колеса); T
1
— вращающий момент на шестерне, Н
• мм; K
Hβ
— коэффициент нагрузки (см. табл. 3.4); Ω= 1,1 ÷ 1,3 — коэффициент, учитывающий
неравномерность распределения нагрузки среди сателлитов;
1 2
i
— передаточное отношение; [Ψ
bd
]
i
=
0,75 — коэффициент длины зуба (ширины колеса); [σ]
н
— допускаемое контактное напряжение, МПа
(см. шаг 3.45).
При расчете планетарных передач выбор числа зубьев колес зависит не только от передаточного
отношения /, но и от условий собираемости передач. При этом сумма зубьев центральных колес должна
быть кратной числу сателлитов (лучше 3).
Какие параметры определяются в проектировочном расчете на контактную прочность передач.
§ 22. Волновые зубчатые передачи. Устройство передачи и расчет на прочность
3.92. Волновые передачи основаны на принципе передачи вращательного движения за счет бегущей волновой
деформации одного из зубчатых колес.
Кинематически эти передачи представляют собой разновидность планетарной передачи с одним
гибким зубчатым колесом. На рис. 3.61 изображены основные элементы волновой передачи:
неподвижное колесо 7 с внутренними зубьями, вращающееся упругое колесо 2 с наружными зубьями и
водило h. Неподвижное колесо закрепляется в корпусе и выполняется в виде обычного зубчатого колеса
с внутренним зацеплением. Гибкое зубчатое колесо имеет форму стакана с легко деформирующейся
тонкой стенкой: в утолщенной части (левой) нарезаются зубья, правая часть имеет форму вала. Водило
состоит из овального кулачка и специального подшипника.
Рис. 3.61. Волновая передача
Гибкое колесо деформируется так, что по оси овала I—I зубья зацепляются на полную рабочую
высоту; по оси II—II зубья не зацепляются.
Передача движения осуществляется за счет деформирования зубчатого венца гибкого колеса. При
вращении водила волна деформации бежит по окружности гибкого зубчатого венца; при этом венец
обкатывается по неподвижному жесткому колесу в обратном направлении, вращая стакан и вал.
Поэтому передача и называется волновой, а водило — волновым генератором.
При вращении водила овальной формы образуются две волны. Такую передачу называют
двухволновой. Бывают трехволновые передачи, на рис. 3.62 показана схема такой передачи.

Рис. 3.62. Трехволновая передача
3.93. Достоинство и недостатки волновых передач.
Волновые передачи обладают большой нагрузочной способностью (в зацеплении находится
большое число пар — зубьев) и высоким передаточным числом (/ ^ 300 для одной ступени) при
сравнительно малых габаритах. Это основные достоинства этих передач. Передача может работать,
находясь в герметизированном корпусе, что очень важно для использования волновых передач в
химической, авиационной и других отраслях техники.
Недостатки волновой передачи: сложность изготовления гибкого колеса и волнового генератора;
возможность использования этих передач только при сравнительно невысокой угловой скорости вала
генератора.
Сравните волновую передачу с обычной зубчатой с точки зрения коэффициента перекрытия
зубьев.
Влияет ли на работоспособность волновой передачи точность изготовления деталей
генератора волн?
3.94. Передаточное отношение волновых передач определяется методом остановки водила
(метод Виллиса).
По рис. 3.61 передаточное отношение: при неподвижном жестком колесе
2 2 2 1 2 2
/ / /
h h
i z z z z C
(3.36)
где ω
h
и ω
2
— угловые скорости волнового генератора и гибкого колеса; z
1
, z
2
— числа зубьев
жесткого и гибкого колес; С — число волн; при неподвижном упругом колесе
1 1 2 1 2 1
/ / /
h h
i z z z z C
(З 37)
В формуле (3.36) знак «минус» указывает на разные направления вращения генератора и гибкого
колеса.
3.95. Причины выхода из строя и критерии работоспособности. В процессе работы этой передачи
наблюдается повышенное изнашивание зубьев, разрушение гибких колес и других деталей генератора
волн. Основным критерием работоспособности волновых передач является прочность гибкого колеса
и прочность гибкого подшипника генератора.
Волновые передачи можно применять в качестве редукторов, дифференциалов и вариаторов
скорости.
3.96. Ответить на вопросы контрольной карточки 3.13.
Контрольная карточка 3.12
Вопрос Ответы Код
Какая передача показана на рис. 3.61? Зубчатая с внутренним
зацеплением Зубчатая планетарная
Зубчатая волновая
1
2
3
Как называют деталь h на рис. 3.60? Водило
Сателлиты
4
5
Покажите на рис. 3.60 ведущий вал
зубчатой передачи
1
2
q
h
6
7
8
9
Достаточно привести расчет на
контактную прочность зубьев планетарных
передач по рис. 3.60 только для зацепления...
Внешнего
Внутреннего
Внешнего + внутреннего
10
11
12
Влияют ли параметры сателлитов в
планетарной передаче на значение
передаточного числа
Влияют
Не влияют
13
14
Ответы на вопросы

3.2. Достоинство зубчатой передачи по сравнению с фрикционной (см. шаг 3.2).
3.3. Фрикционные передачи не имеют недостатков зубчатых передач (см. шаг 3.3). Однако
отмеченные в шаге 3.3 недостатки не снижают существенного преимущества зубчатых передач перед
другими, поэтому зубча-твш передачи имеют наиболее широкое применение во всех отраслях ма-
шиностроения.
3.5. Закрытая зубчатая передача отличается от открытой тем, что имеет специальный корпус, в
котором располагаются зубчатые колеса. Для смазывания передачи в корпус заливают масло.
3.7. Способ обработки зубьев, показанный на рис. 3.8, называется обкаткой.
3.9. Наиболее распространенные в машиностроении конструкции зубчатых колес: литые, кованые
или штампованные (перечертите в конспект рис. 3.9, 3.10). Сварные конструкции зубчатых колес
применяют при их больших габаритных размерах, а также в целях снижения массы и экономии
высокопрочных дорогостоящих материалов.
3.10. Можно. Колеса из неметаллических материалов в паре с металлическими работают с малым
шумом. Такую конструкцию целесообразнее применять при передаче незначительных мощностей (и
при больших окружных скоростях).
3.12. Параметры зубчатого зацепления (рис. 3.15) следующие: d — делительный диаметр, d
a
—
диаметр окружности зубчатого колеса, проходящей через вершины зубьев; d
f
— диаметр окружности
зубчатого колеса, проходящей через основания зубьев; р — расстояние по дуге между одноименными
профилями соседних зубьев. Делительная окружность (см. рис. 3.15) условно делит зуб на головку зуба
(h
a
) и ножку зуба (h
f
)
3.13. Окружной модуль m
t
= p
t
/π. Шестерня и колесо одной и той же пары не могут иметь разный
модуль, а у двух пар может.
3.16. На зубчатом колесе линию зацепления увидеть нельзя. Длина линии зацепления и угол
зацепления а
ш
— только теоретически представляемые геометрические параметры (см. рис. 3.19).
Окружности, проведенные из центров О
1
и О
2
радиусами О
1
A и O
2
D, называются основными.
3.17. Для обеспечения постоянного передаточного числа профили зубьев должны очерчиваться по
кривым, удовлетворяющим основному закону (теореме) зацепления.
3.18. Для профилей зубьев применяются кривые — эвольвенты, эпициклоиды, гипоциклоиды,
окружности. Наибольшее распространение в машиностроении получили эвольвентные профили.
3.20. Подрезание некорригированных зубьев возникает при z < z
min
3.21. На рис. 3.24 показано: а — отрицательное смещение, в — положительное. При положительном
коэффициенте смещения зуб у основания утолщается, а у вершины заостряется, в результате чего
прочность на изгиб и контактная прочность зуба повышаются.
3.22. Значительный перегрев передач и чрезмерный шум.
3.23. Вследствие периодического действия нагрузки могут возникнуть усталостные трещины у
основания зуба, приводящие в конечном итоге к его поломке. Сопротивление зубьев излому можно
повысить, например, с помощью положительной коррекции, механических свойств материала колес,
жесткости всей передачи, увеличив модуль передачи.
3.24. Способность сопротивляться выкрашиванию можно повысить, создав более гладкую и
прочную поверхность зубьев, увеличив радиус кривизны профилей зубьев в зоне контакта и правильно
подобрав смазочный материал, увеличить твердость поверхности зубьев методом поверхностного
упрочнения.
3.25. Вид повреждения зубьев — изнашивание их рабочих поверхностей в какой-то степени
нарушает нормальную работу передачи, но не выводит ее из строя до тех пор, пока величина износа не
достигнет значения, недо-пускаемого правилами технической эксплуатации. Изнашивание зубьев
можно понизить, уменьшив скольжение профилей и контактные напряжения, а также увеличив
износостойкость рабочих поверхностей и правильно подобрав смазочный материал.
3.26. Заедание можно предупредить: в тихоходных передачах применением очень вязких смазочных
материалов, а в быстроходных — противоза-дирных смазочных материалов.
3.29. Геометрические оси ведущего и ведомого валов цилиндрической прямозубой передачи
параллельны.
3.30. Выполните действия вопроса шага 3.30 и по табл. 3.3 проверьте ответ и запишите в конспект.
3.31. z
1
= z
[
+ Z
2
= Zi+ z
x
u = Z
1
(1 + и), так как и = z
2
/Z
1
, то z
t
= z
1
u. Из изложенного выше z
x
= Z
∑
/1 + и), Z
2
= Z
∑
- Zi.
3.33. Наибольшее напряжение изгиба имеет место у ножки зуба, в зоне перехода эвольвенты в
галтель (сечение — ВС).
3.34. Коэффициенты K
Fβ
, K
Fv
, Y
F
определяют по табл. 3.4—3.6.

3.36. Проверочный расчет зубчатой передачи на изгиб всегда, когда даны параметры передачи т, z,
Ψ
bd
и другие, а также известные силовые параметры T и кинематические со параметры передачи.
Требуется сделать заключение о прочности передачи на изгиб (или по значению a
F
выбрать материал
для открытых зубчатых колес).
3.37. Зубья шестерни при одних и тех же условиях испытывают большие изгибающие напряжения
(коэффициент формы зуба и концентрации напряжений шестерни меньше, чем колеса, так как Z
1
< Z
2
).
3.38. Для получения значения модуля в миллиметрах необходимо в формулу (3.8) подставить
значения Т
2
, в Н • мм и [σ]
F
в МПа.
3.39. Для подстановки в формулу (3.8) следует принимать допускаемое напряжение изгиба [a]
F
,
которое определяется расчетным путем в зависимости от σ
Fдшь b
, принимаемого из табл. 3.8.
3.43. σ
н
— возникающее нормальное контактное напряжение, МПа; Z
H
. Z
M
, Z
ε
— коэффициенты,
учитывающие форму сопряженных поверхностей зубьев, механические свойства материалов и
суммарную длину контактных линий; а
а
— межосевое расстояние, мм; и — передаточное число; Т
2
—
момент на валу колеса, Н • мм; Ψ
ba
— коэффициент длины зуба (ширина венца колеса) относительно
межосевого расстояния; К
нβ
— коэффициент неравномерности распределения нагрузки; K
Hv
—
коэффициент динамической нагрузки; [σ]
н
— допускаемое контактное напряжение, МПа.
3.44. Нормальные контактные напряжения одинаковы для зубьев шестерни и колеса.
3.45. Расчет [ст]
Я1
и [а]
Н2
(условие — см. шаг 3.40).
1. База испытаний — см. табл. 3.10. Для шестерни HВ
1
= 475; для колеса НВ
2
= 280 (среднее
значение) методом интерполяции .находим:
6 6 6
1
90 70
70 10 10 80 10 ,
50
HO
N
6 6 6
2
26,4 17
70 10 30 10 22,94 10 .
50
HO
N
Расчетная циклическая долговечность (см. шаг 3.40): N
H1
= 8,6 • 10
8
; N
H2
= 1,92 · 10
8
.
Так как N
H
> N
H0
, то K
HL
= 1.
2. По табл. 3.9 пределы контактной выносливости:
0
Flimb1
=18HRC+ 150 = 18 47,5 + 150 = 1000 MÏ à
;
0
Flimb1
=2HB+70 = 2 280 + 70 = 630 Ì Ï à
(HB
1
= 475 ≈ HRC = 47,5).
3. Принимаем Z
R
= 0,95, S
H
= 1,2 и определяем допускаемые контактные напряжения:
[σ]
H1
= (1000 • 0,95)/1,2 = 800 МПа; [σ]
H2
= (630 • 0,95)/1,2 = 570 МПа.
За расчетное допускаемое контактное напряжение принимают меньшее из двух полученных
значений.
3.50. Осевая сила (см. рис. 3.40) на опоры передается, но полушевроны будут нагружены
неодинаково. Колесо (см. рис. 3.40) называется зубчатым колесом с тремя полушевронами.
3.52. Определение модулей для косозубой передачи: нормальный модуль
2 cos
cos ; ; ;
/ cos 2
a
n t n n
d
a
m m m m
z z
торцовый модуль
т
t
=d/z;
cos
t n
m m
; m
t
= 2a/z
z
.
3.54. В шевронной передаче (см. рис. 3.38) осевые силы взаимно уничтожаются как
противоположные по направлению (см. рис. 3.39).
3.55. Винтовая зубчатая передача является передачей со скрещивающимися осями (рис. 3.41).
3.57. Осевая сила возрастает с увеличением угла β. По условиям прочности габаритные размеры
косозубых передач меньше, чем у прямозубых.
3.59. По табл. 3.6 Y
F
=3,66
(выбирают по
3
24 24
46
cos 0,83 0,512
v
z
z
)
3.60. Введением в формулы коэффициента концентрации напряжений К
Нβ
и коэффициента
динамичности K
Hv
.
3.61. В формулу (3.26) необходимо подставлять меньшее по значению [σ]
H
так как необходимо
обеспечить прочность передачи по менее прочному материалу.

3.64. Формулы:
1. u=z
2
/z
1
2. Ознакомьтесь с табл. 3.8, 3.11.
6
/ 350 ;
FL FO F
K N N HB
9
/ 350 ;
FL FO F
K N N HB
N
F
=60nct
∑
; N
F
=573ωct
∑
4. β = 8 ÷ 18°, z
1
= 17.
5. Z
2
=Z
1
U.
6. z
v1
= z
1
/ cos
3
β; z
v2
=z
2
/cos
3
β
7. Ψ
bd
(табл. 3.7).
8.
2
3
2
1
F F F
m m
bd
F
T K Y K
m K
uz
9.
1 2
1 2
; ;
cos
n n n t n
z
d m p m p m
s
t
=е
t
=пт
t
/2; h=2,25m
n
; h
a
=m
n
; h
f
=1,25т
n
.
с=0,25т
п
.
10.
1 1
/ 2v d
3.66. На рис. 3.49 шестерня и колесо выполнены с круговыми зубыли.
3.69. На рис. 3.52 высота головки h
ae
= т
е
; h
am
= т.
3.74. Расчет геометрических параметров передачи производят по модулю т
е
, а на изгибную
прочность по т.
3.75. Y
F2
= 3,60 (выбирается в зависимости от z
v2
= z
2
/ соsδ
2
= 72/0,242 = 300).
3.76. Коэффициент K
Fe
учитывает снижение нагрузочной способности зубьев конической передачи
по сравнению с зубьями цилиндрических ю: редач (K
F0
< 1). В прямозубой передаче коэффициент
отсутствует, в косозубой передаче аналогичный коэффициент K
Fa
учитывает повышение прочности
зубьев на изгиб по сравнению с прямыми зубьями.
3.77. Для снижения нормальных контактных напряжений (не измеш силовых параметров и
передаточного числа) следует длину зуба увелн«-
:
до b
mm
= y
bdmm
d
l
или увеличить модуль т, что
соответствует увеличению i
3.78. Формулы для определения [σ]
н
(см. шаг 3.45):
3.80. Формулы:
3.82. В машиностроении распространены эвольвентные (и крайне редко — циклоидальные).
Зубчатые передачи с зацеплением Новикова имеют профили зубьев, очерченные дугами окружностей;
рабочие поверхности представляют собой круговинтовые поверхности.
3.83. Недостаток зубчатых передач с зацеплением Новикова — высокая чувствительность к
точности сборки, сложность изготовления.
Достоинства. По сравнению с эвольвентным зацеплением передачи с зацеплением Новикова при
одних и тех же габаритах могут передать значительно большую мощность. При передаче одной и той же
мощности передачи с зацеплением Новикова имеют почти в 2 раза меньшие габариты.
3.84. Повторите информацию шага 3.83, выполните рекомендации вопроса и проверьте ответ по
табл. 3.17. Межосевое расстояние
a
w
= (d
x
+ d
2
)/2 = (d
x
+ d
x
u)/2 =[d
l
(l + и)]/2.
Так как и = djd
x
, то d
2
= d
x
u.
3.85. Формула проверочного расчета цилиндрической прямозубой передачи с эвольвентным
зацеплением:
Формула проектировочного расчета этой же передачи:
3.87. Планетарные передачи — разновидность зубчатых цилиндрических и конических передач с
эвольвентным и другими профилями зубьев (зубья могут быть прямые и косые).
3.88. Планетарные передачи широко применяют в автомобилях, тракторах, станках, приборах.
3.90. В передаче (см. рис. 3.63) модули и силы в зацеплении одинаковы. С учетом того, что
внутреннее зацепление по своим свойствам прочнее внешнего, при одинаковых материалах колес
достаточно рассчитать только внешнее зацепление.
3.91. В проектировочном расчете планетарных передач для каждой пары зацепления определяется
делительный диаметр d
x
, по которому вычисляют модуль т = d
x
lz
v
Округлив найденное значение т до
ближайшего большего стандартного (табл. 3.1), по табл. 3.3 определяют геометрические параметры
зубчатой пары шестерня—колесо.
3.93. Волновая передача может обеспечить одновременное зацепление большого числа пар зубьев (в
обычной передаче е
а
= 1,4 + 1,6). Точность изготовления деталей генератора волн и их взаимное
расположение на валу оказывают существенное влияние на качество волновых передач. Неурав-
новешенность генератора волн приведет к возникновению значительных динамических нагрузок,
вибрации и т. д.
Глава 4
ПЕРЕДАЧА ВИНТ-ГАЙКА
§ 1. Устройство и назначение, достоинства и недостатки

4.1. Передача винт-гайка (рис. 4.1) состоит из винта 1 и гайки 2, соприкасающихся винтовыми
поверхностями.
Передача винт-гайка предназначена для преобразования вращательнег; движения в
поступательное (при больших углах подъема винтовой линии, порядка у> 12°). Когда угол подъема
больше угла трения, эту переда-г. можно использовать для преобразования поступательного
движения БС вращательное.
Рис. 4.1. Передача винт-гайка
Различают два типа передач винт-гайка:
• передачи трения скольжения или винтовые пары трения скольженн-
(рис. 4.1-4.3);
• передачи трения качения или шариковые винтовые пары (рис. 4.41
Ведущим элементом в передаче, как правило, является винт, вед:-
мым — гайка. Конструктивно передача винт-гайка может быть выполнена:
• с вращательным движением винта и поступательным движением гай
ки (см. рис. 4.1);
• с вращающимся и одновременно поступательно перемещающимс
:
винтом при неподвижной гайке (см. рис. 4.2);
• с вращательным движением гайки 1 и поступательным движение'
винта 2 (см. рис. 4.3).
Передачи винт-гайка находят применение в устройствах, где требует; получать большой
выигрыш в силе, например в домкратах, винтовых прессах, нагрузочных устройствах
испытательных машин, механизмах
Рис. 4.2. Винтовой домкрат: 1—
винт; 2 — гайка; 3 —стопорный
винт; 4 — рукоятка; 5 — чашка
домкрата; 6— шип, 7 — корпус
Рис. 4.3.Передача
винт-гайка: / — гайка;
2 — винт
Рис. 4.4.Передача
винт-гайка с трением
качения
металлорежущих станков или в измерительных и других механизмах для точных делительных
перемещений.
Опишите работу простейшего винтового устройства — домкрата (см. рис. 4.2).
