Мархель И.И. Детали машин
Подождите немного. Документ загружается.

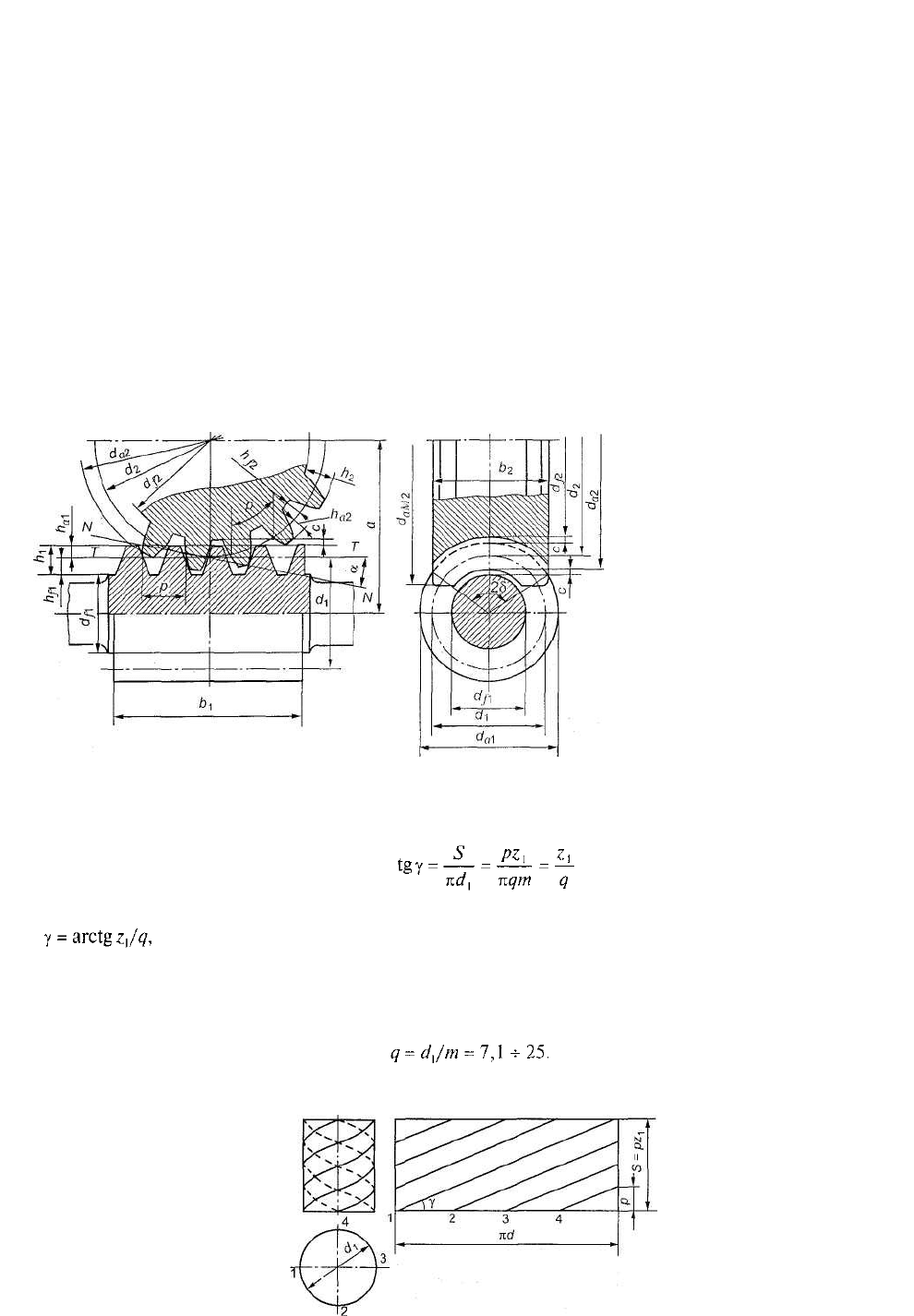
§ 2. Геометрическое соотношение размеров червячной некорригированной
передачи с архимедовым червяком
5.9. В червячной передаче в качестве расчетного модуля принимают осевой модуль червяка т,
равный окружному модулю червячного колеса т,. Значения модуля т червячных передач
стандартизированы (табл. 5.1).
В цилиндрических червячных передачах с архимедовыми червяками 'шаг червяка р и шаг зубьев
червячного колеса равны между собой (рис. 5.5):
р = πт. (5.2)
Рис. 5.5. Геометрические параметры червячной передачи
Угол у (рис. 5.6), образованный винтовой линией по делительному цилиндру червяка с плоскостью,
перпендикулярной к его оси, называют углом подъема витка червяка на делительном цилиндре:
(5.3)
или
где Z\ — число витков червяка; S = pz
t
— ход винтовой линии червяка.
В червячных передачах вводят q — коэффициент диаметра червяка (отношение делительного
диаметра червяка d
x
к его расчетному модулю т).
Принимают
(5.4)

Рис. 5.6. Схема образования винтовой линии червяка
Для сокращения числа размеров фрез, требуемых для нарезания червячных колес, рекомендуется
придерживаться значений q, предусмотренных стандартом на червячные передачи (см. табл. 5.1).
Некоторые значения угла подъема витка червяка: 3°34'35"; 4°05'08";4°45'49"; 5°42'38";
6°20'25"; 7°07'30"; 11°18'36"; 12°31'44"; 14°02'10"; 14°55'53"; 15°56'43"; 18°25'06"; 21°48'05"; 23°57'45";
26°33'54"; 28°04'21".
Как называются параметры р, q, у?
5.10. Геометрические параметры червяка и червячного колеса (см. рис. 5.5) некорригированной
червячной передачи.
Высота витка h
x
= 2,2т; высота зуба червячного колеса h
2
= 2,2/и; высота головки винта h
aX
= m;
высота головки зуба h
a2
= m; высота ножки витка h
fX
= \,2m; высота ножки зуба колеса h
f2
= 1,2m;
расчетная толщина витка р = 0,5пт; радиальный зазор с = 0,2т.
Делительные диаметры:
червяка d
x
= mq;
червячного колеса d
2
= mz
2
Диаметры вершин:
витков червяка d
a1
= d
x
+ 2h
a1
;
зубьев червячного колеса d
a2
= d
2
+ 2h
a2
.
Диаметры впадин:
червяка d
fl
= d
{
- 2h
fl
;
червячного колеса d
f2
= d
2
- 2h
f2
.
Межосевое расстояние a=(d
x
+ d
2
)/2 = 0,5(q + z
2
)m.
Условный угол обхвата червяка венцом 25 (см. рис. 5.5) определяется точками пересечения дуги
окружности диаметром d
aX
-0,5т с контуром венца;
Конструктивные элементы передачи: длину нарезной части червяка Ь
х
, ширину венца колеса Ъ
2
и
наружный диаметр колеса d
aM2
определяют в зависимости от числа витков червяка z
x
, модуля т и числа
зубьев колеса z
2
по соотношениям, приведенным в табл. 5.2.
Таблица 5.2. Формулы для расчета конструктивных элементов червячной передачи
Число заходов
червяка z\
Длина
нарезанной части
червяка Ь\
Ширина венца
колеса Ь
2
Наружный
диаметр колеса d
lM2
1
2
4
Как рассчитывают делительные диаметры червяка и червячного колеса? Сравните с
аналогичным расчетом d\ и di для зубчатых передач.

5.11. Ответить на вопросы контрольной карточки 5.1.
Контрольная карточка 5.1
Вопрос Ответы К
од
Определите, сколько витков имеет
червяк, показанный на рис. 5.6
1
2
3
4
Определить нельзя
1
2
3
4
5
Определите, передаточное число
червячной передачи, если число зубьев
колеса равно Z2 = 30, число витков червяка
z\ = 2
60
15
1/15
Определить нельзя
6
7
8
9
Какой профиль зуба имеет червячное
колесо цилиндрического архимедова
червяка в главном сечении (в плоскости,
проходящей через ось червяка)?
Трапецеидальный
Эвольвентный
Циклоидальный
Любой из перечисленных
10
11
12
13
Определите делительный диаметр
червяка, если d
2
= 150 мм, zi = 30, q= 10
20
50
15
170
14
15
16
17
Назовите распространенные варианты
сочетания материалов для червяка и
червячного колеса
Сталь—чугун
Чугун—чугун
Бронза—сталь
Сталь—бронза
Чугун—бронза
18
19
20
21
22
§ 3. Основные критерии работоспособности червячных передач и расчет их на
прочность
5.12.5 червячных передачах наблюдаются следующие виды разрушений зубьев:
• заедание; особо опасно при колесах из твердых безоловянистых бронз и чугуна (см. шаг 3.26).
Сопротивление заеданию повышают соответ- ствующим подбором материалов для червяка и
червячного колеса, тщательной отделкой поверхностей зубьев и витков, а также использованием
только рекомендуемых смазочных материалов;
• изнашивание зубьев; происходит по той же причине, что и заедание, а
также при ухудшении условий смазывания (загрязнении смазочного
материала, длительной работе с частыми пусками и остановками пе
редачи);
• изломы зубьев колеса; наблюдаются после их изнашивания, чаще при
наличии динамических нагрузок.
Одной из причин повышенного изнашивания зубьев червячного колеса (и заедания) является
скольжение витков червяка по зубьям червячного колеса при отсутствии разделяющей их масляной
пленки. Скорость скольжения v
CK
направлена по касательной к винтовой линии делительного
диаметра червяка d
{
и определяется из параллелограмма скоростей (см. рис. 5.7):
где и, и v
2
— окружные скорости червяка и колеса, м/с; d
x
, мм; со, — угловая скорость червяка,
рад/с.
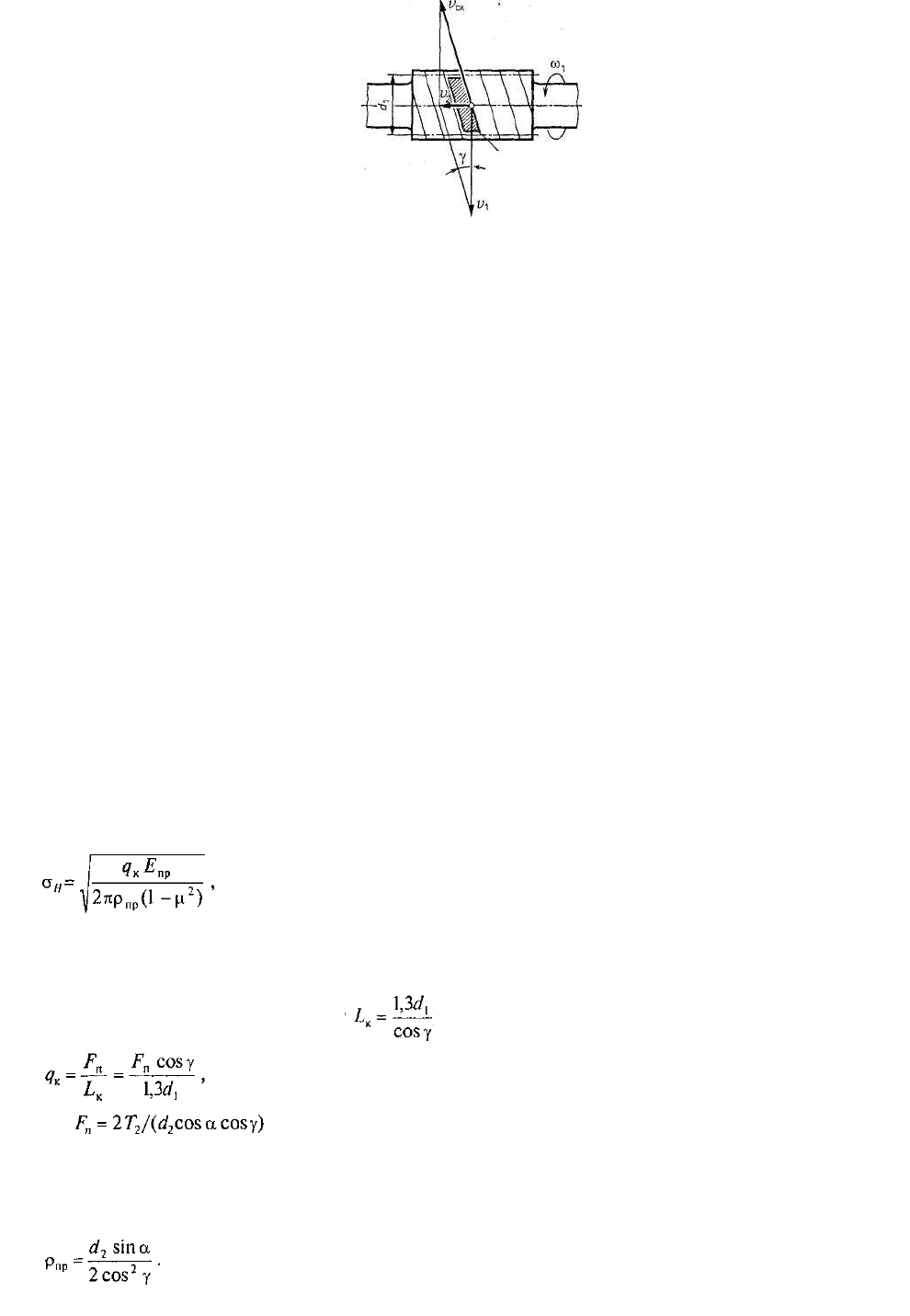
Рис. 5.7. Скольжение в червячной передаче
Перечислите виды разрушений зубьев для зубчатых передач. Какой вид разрушений является более
распространенным для закрытых зубчатой и червячной передач? К чему приводит повышение скорости
скольжения в червячной передаче?
5.13. Червячные передачи так же, как и зубчатые, рассчитывают по контактным напряжениям и
напряжениям изгиба.
В связи с тем, что в червячных передачах при работе происходит выделение большого количества
тепла (что, в свою очередь, ухудшает условия смазывания, увеличивает изнашивание и опасность
заедания), закрытые передачи дополнительно рассчитывают на нагрев.
Интенсивность изнашивания червячных передач во многом зависит от величины контактных
напряжений, поэтому расчет по контактным напряжениям является основным. Он должен
обеспечивать не только отсутствие
усталостного выкрашивания зубьев, но и заедания. Для червячных закрытых передач расчет на
контактную прочность является, как правило, и расчетом на заедание.
Расчет червячных передач по напряжениям изгиба производят, как проверочный. Значение
расчетных напряжений изгиба в зубьях колес, размеры которых найдены из расчета на контактную
прочность, как правило, значительно ниже допускаемых.
После проведения этих расчетов производят тепловой расчет передачи.
Как производят расчет закрытых червячных передач с машинным приводом!
§ 4. Расчет червячной передачи на контактную прочность
5.14. При аналогии с расчетом зубьев зубчатых колес наибольшие контактные напряжения в зоне
зацепления определяют по формуле Герца:
(5.5)
где Е
пр
— приведенный модуль упругости материалов червяка и колеса; р
пр
— приведенный радиус
кривизны профилей сцепляющихся зуба колеса и витка червяка; ц — коэффициент Пуассона (для стали,
бронзы и чугуна ц = 0,3); q
K
— нормальная нагрузка, приходящаяся на единицу длины контактных
линии L
K
колеса и червяка (принимают
(5.6)
где — нормальная нагрузка к поверхности зуба червячного колеса и витка
червяка (ее условно считают приложенной в полюсе зацепления); Т
2
— вращающий момент на
червячном колесе; а = 20° — угол зацепления; у = 4 ■=- 26° — угол подъема линии витка по
делительному цилиндру; d
2
— делительный диаметр червячного колеса. Выражение для приведенного
радиуса
(5.7)
Значение приведенного модуля упругости
Зуб колеса
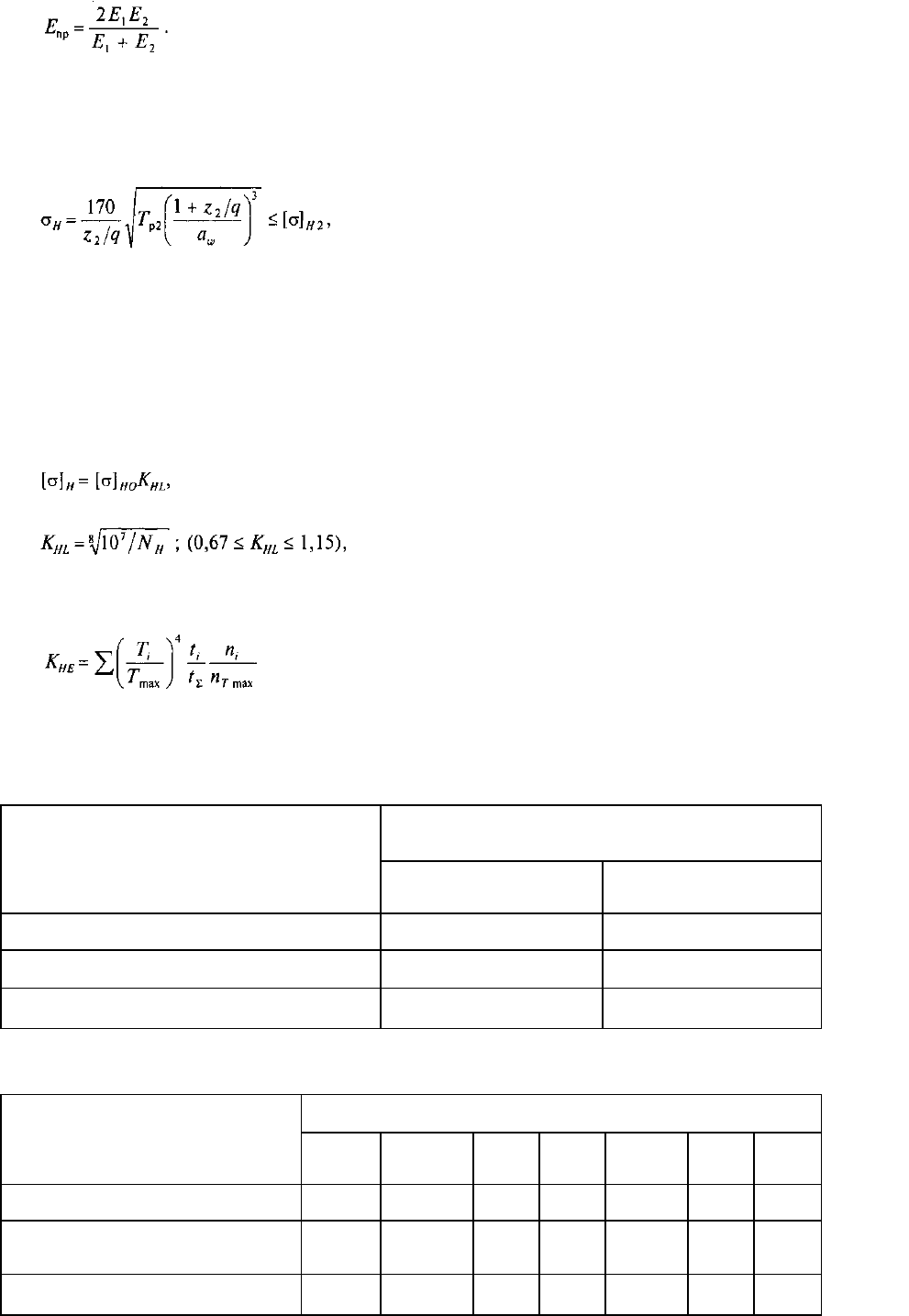
(5.8)
Для червячных передач принимают E
пр
=2,1 · 10
5
МПа (стальной червяк); Е
2
= 0,9 · 10 МПа
(бронзовое или чугунное колесо).
Подставляя в формулу (5.5) вместо q
K
, р
пр
, Е
пр
и ц их значения и решая это уравнение относительно
межосевого расстояния а
ш
, получим формулы для проверочного расчета червячных передач по
контактным напряжениям.
(5.9)
где о
н
— расчетное контактное напряжение в поверхностных слоях зубьев колеса, МПа; q —
коэффициент диаметра червяка; а
ш
— межосевое расстояние, мм; Т
р2
= T
2
K^K
V
— расчетный момент на
червячном колесе, Н · мм; z
2
— число зубьев колеса; К§ — коэффициент неравномерности нагрузки (при
постоянной нагрузке К^ = 1,0, при переменной нагрузке в зависимости от жесткости червяка АГ
р
=1,1-^-
1,3); А^ — коэффициент динамической нагрузки (при окружной скорости и
2
< 3 м/с принимается K
v
= 1,1
÷ 1,0, при v
2
> 3 м/с - К.
о
= 1,1 ÷ 1,3).
5.15. Проверочный расчет.
Допускаемое напряжение [а]
я
получают умножением табличных значений [а]
н0
на коэффициент
долговечности K
HL
, т. е.
при этом
где N
H
— циклическая долговечность.
Для постоянной нагрузки N
H
= 60и
2
^; для переменной N
H
= 60n
2
t
z
K
HE
, где п
2
— частота вращения
червяка, об/мин; t
z
— срок службы, ч;
— коэффициент приведения переменной на-
грузки к постоянной. Здесь Т
р
T
mm
— промежуточные и максимальные моменты; и,., n
Tmm
, Г/, t
s
—
соответствующие этим моментам частота вращения и продолжительность работы.
Значения [и]
но
можно выбрать по табл. 5.3 и 5.4.
Таблица 5.3. Значения [сг]#о> МПа, для оловянистых бронз
Материалы и способ литья Твердость поверхности витков червяка
до HRC 45 св. HRC 45
БрО10Ф1, в песчаные формы 130 160
БрО10Ф1, в кокиль 190 225
БрОНФ, центробежное 210 250
Таблица 5.4. Значение [а]#о, МПа, для твердых бронз и чугунов по условию стойкости передачи к заеданию
Червячное колесо — червяк Скорость скольжения о
ск
, м/с
0,5 1 2 3 4 5 8
БрА9Ж4 — закаленная сталь 250 230 210 180 160 120 90
СЧ15 или СЧ20 — сталь 20 или 20Х
(цементованная)
130 115 90 — — — —
СЧ10 или СЧ15 — сталь 45 или Стб ПО 90 70 — — — —

Зависит ли ац от передаточного числа?. Что обозначает параметр q? Как влияет его величина на
работоспособность передачи?
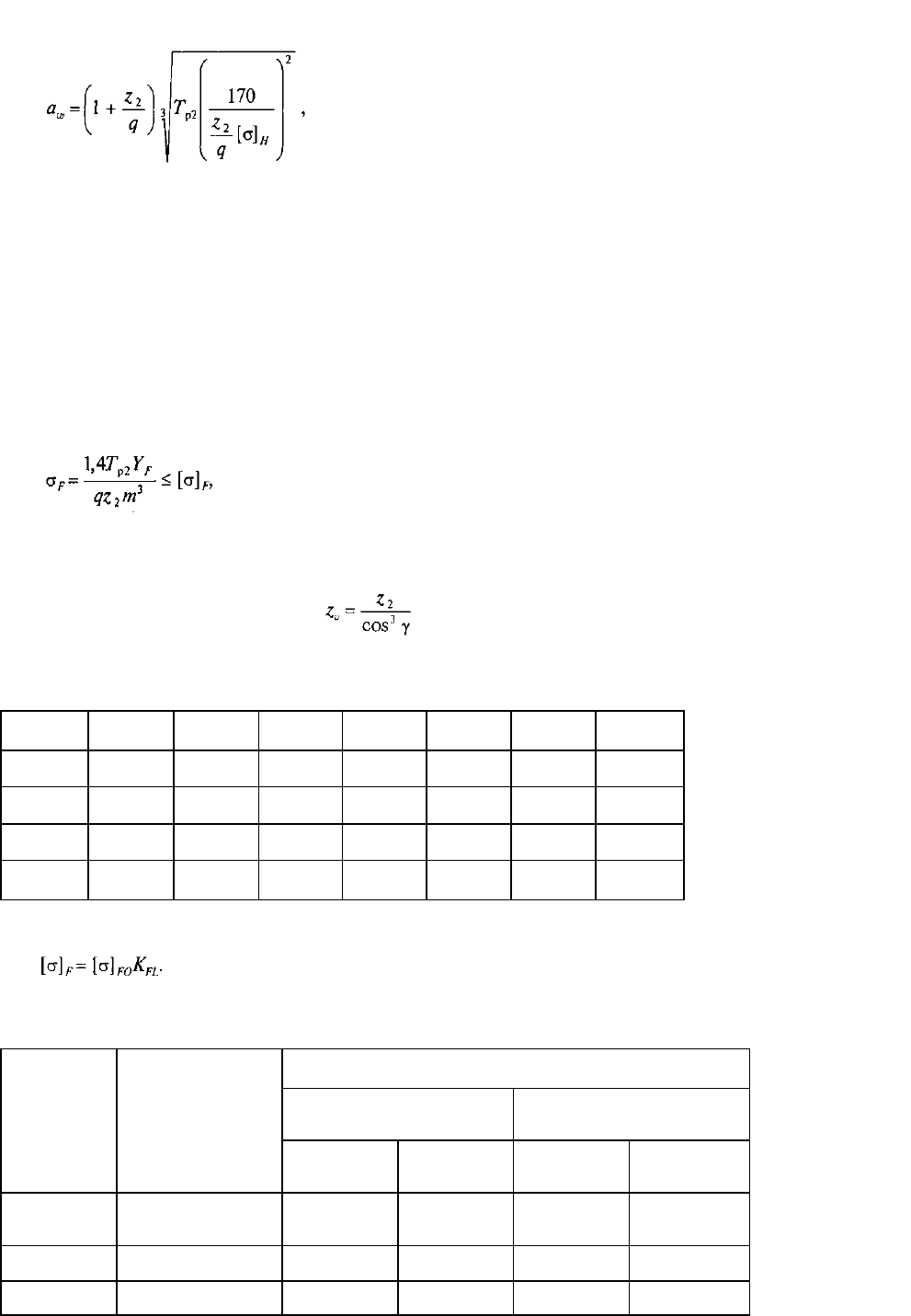
5.16. Проектировочный расчет. Решая уравнение (5.9) относительно параметра а
ш
, (межосевое
расстояние), получим формулу проектировочного расчета червячных передач:
(5.10)
где а
ш
, мм; Г
р2
, Н • мм; [а]
№
МПа.
§ 5. Расчет червячной передачи на прочность по напряжениям изгиба
Расчет зубьев червячных колес на изгиб аналогичен расчету цилиндрических зубчатых колес.
На изгиб рассчитывают лишь зубья червячного колеса (витки червяка обладают избыточной
прочностью на изгиб).
5.17. Проверочный расчет. В формулу (3.23) вводят соответствующие поправки для числового
коэффициента, учитывающие увеличение прочности зубьев червячного колеса (примерно на 40 %) по
сравнению с косозубыми цилиндрическими передачами за счет дугообразной формы зуба червячного
колеса.
Прочность на изгиб зуба червячного колеса проверяют по формуле
(5.11)
где Г
р2
= T
2
K
p
K
v
— расчетный момент на червячном колесе, Н · мм (см. шаг 5.15); q — коэффициент
диаметра червяка (см. табл. 5.1); z
2
— число зубьев колеса; Y
F
— коэффициент формы зуба для
червячных передач (выбирают
по эквивалентному числу зубьев из табл. 5.5); CT
F
H [a]
F
— расчет-cos у
ное и допускаемое напряжения изгиба, МПа.
Таблица 5.5. Значения коэффициента формы зуба Y
F
червячного колеса
Z-o
YF
Zu
YF
Zv
Y
F
Zv
Y
F
26 1,85 35 1,64 50 1,45 150 1,27
28 1,80 37 1,61 6 1,40 300 1,24
30 1,76 40 1,55 80 1,34
32
1,71 45 1,48 100 1,30
По аналогии с шагом 5.15 допускаемое напряжение изгиба
Допускаемое напряжение на изгиб можно выбрать по табл. 5.6;
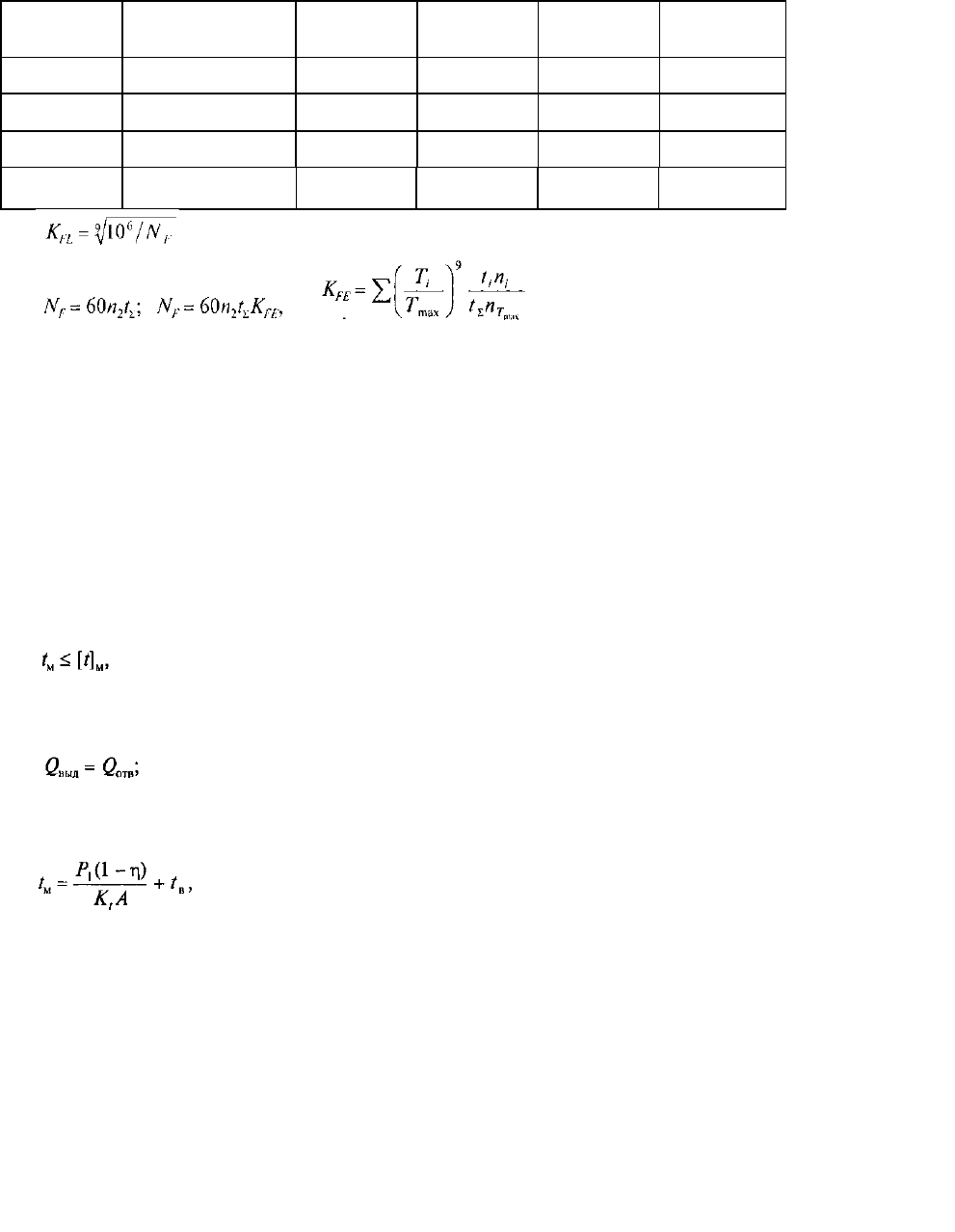
Таблица 5.6. Допускаемое напряжение на изгиб a
f
o, МПа, для различных способов литья
Материал
ы
Способ литья Твердость поверхности витков червяка
до HRC 45 св. HRC 45
нереверси
вная
реверсивн
ая
нереверси
вная
реверсивна
я
БрОЮФ В песчаные
формы
40 29 50 36
БрО10Ф1 В кокиль 58 42 72 52
БрОНФ Центробежное 65 46 81 57
БрАЖ9-4 В песчаные
формы
78 64 100 75
СЧ10 Тоже
34
21 42 26
СЧ15 38 24 48 30
СЧ20 43 27 54 34
СЧ25
48
30 60 37
— коэффициент долговечности (0,543 < K
FL
< 1,0);
где — коэффициент
приведения переменной нагрузки к постоянной.
Для каких целей производят проверочный расчет червячных передач по напряжениям изгиба?
§ 6. Тепловой расчет червячной передачи
5.18. В червячной передаче имеют место сравнительно большие потери передаваемой мощности
на трение, передача работает с большим тепловыделением.
Если отвод тепла будет недостаточен, передача перегреется. Так как смазочные свойства масла при
нагреве резко ухудшаются, то возникает опасность заедания передачи и выхода ее из строя. Для
обеспечения нормальной работоспособности для червячных редукторов (закрытой передачи)
производят тепловой расчет. Тепловой расчет червячной передачи при установившемся режиме
работы производят на основе теплового баланса, т. е. приравнивания тепловыделения теплоотводу.
Условие нормального теплового режима:
(5.13)
где t
M
— температура масла в корпусе редуктора; [t]
м
— допускаемая температура масла в корпусе
редуктора (t
M
= 60 -ь 70 °С, в исключительных случаях t
u
= 90 °С); t
u
— определяют из условия
теплового баланса
Q
выд
— количество теплоты, выделяемое передачей при непрерывной работе; Q
0TD
— количество
теплоты, отводимое свободной поверхностью корпуса передачи за то же время.
Итак, на основании теплового баланса можно определить температуру масла
(5.14)
где Р, — мощность, передаваемая червяком, Вт;
ц — КПД передачи;
А — площадь поверхности корпуса передачи, соприкасающаяся с воздухом, м
2
;
t
B
— температура окружающего воздуха, °С;
К, — коэффициент теплопередачи — количество теплоты, передаваемое в окружающую среду с
единицы поверхности в 1 с при разности. температур в 1 °С, Вт/(м
2
• °С).
При нормальной циркуляции воздуха вокруг корпуса K
t
= (14 ÷ 17,5) Вт/(м
2
·
0
С), при плохой – К
t
=
(8 ÷ 10,5) Вт/(м
2
· °С).
Тепловой расчет червячной передачи выполняют как проверочный.
При t
M
> [t]
M
необходимо либо увеличить поверхность охлаждения (применяя охлаждающие ребра и
т. п.), либо применить искусственное охлаждение (обдувание корпуса воздухом с помощью
вентилятора, посредством змеевика с циркулирующей водой, помещаемого в масло, и т. п.).
Поясните, за счет чего осуществляется искусственное охлаждение редуктора (рис. 5.8).
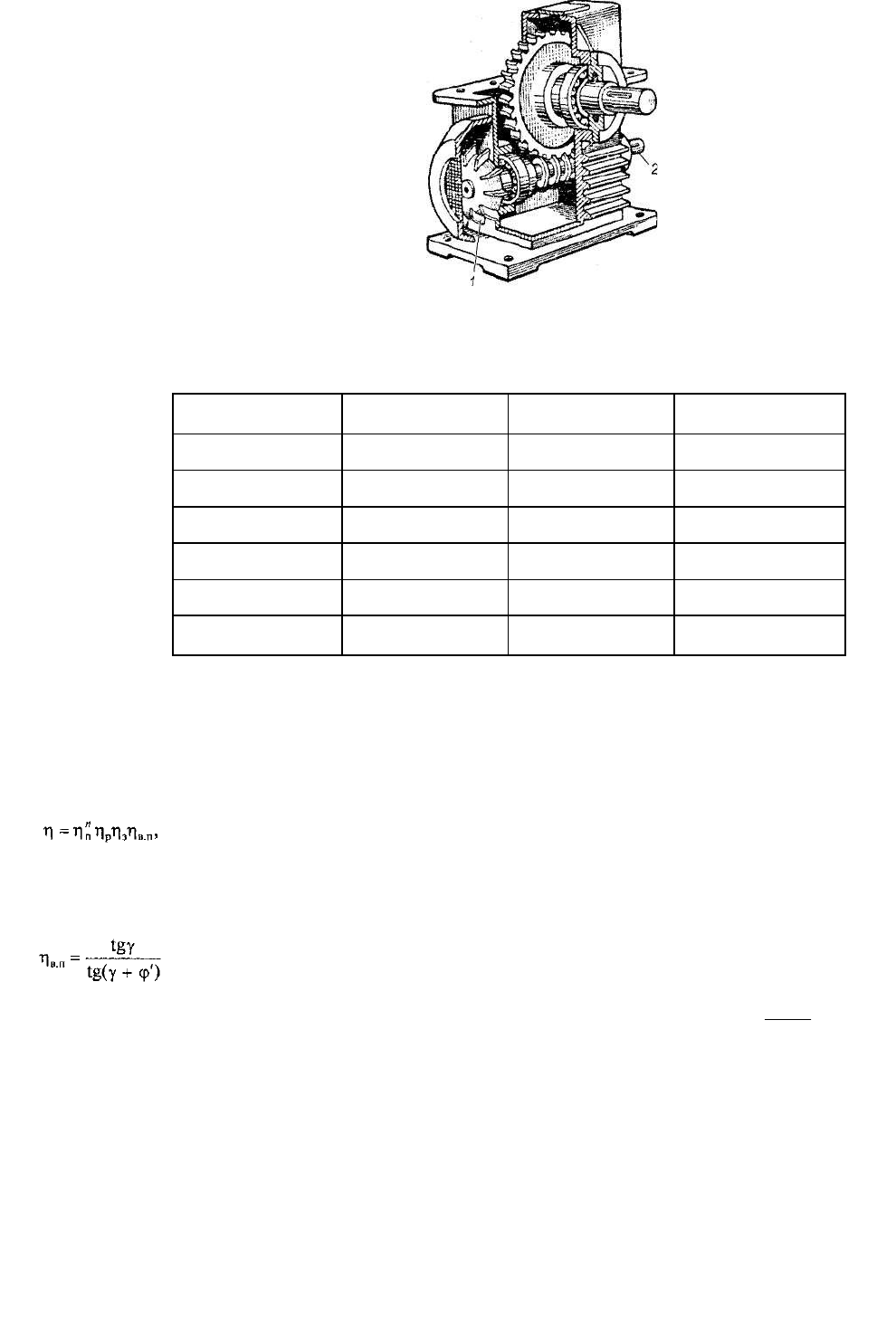
Рис. 5.8. Червячный редуктор с нижним расположением червяка: 1 —
вентилятор; 2 — ведущий вал редуктора
Таблица 5.7. Зависимость угла трения ер' от скорости скольжения v
CK
(червяк стальной, колесо
бронзовое)
v
ск
, м/с φ' v
ск
, м/с φ'
0,01 5°40-6°50 2,5 Г40-2°20
0,1 4°30-5°10 3,0 Г30-2°00
0,5 3°10-3°40 4,0 Г20-Г40
1,0 2°30-3°10 7,0 ГОО-ГЗО
1,5 2°20-2°50 10,0 0°55-Г20
2,0 2°00-2°30
5.19. КПД закрытой червячной передачи должен учитывать потери в зацеплении и подшипниках, а
также потери на разбрызгивание, перемешивание масла и др.
Среднее значение КПД при однозаходном червяке можно принимать равным 0,7 + 0,75; при
двухзаходном 0,75 н- 0,82; трех- и четырехзаходном 0,83 + 0,92. Общий КПД для закрытой червячной
передачи можно определить по формуле (уточненный расчет)
где степень п — число пар подшипников; г|
п
— КПД, учитывающий потери в одной паре; г|
р
—
КПД, учитывающий потери в подшипниках, на разбрызгивание и перемешивание масла; г|
3
— КПД,
учитывающий дополнительные потери в зацеплении аналогичны потерям в зубчатых передачах;
КПД, учитывающий основные потери в зацеплении как в винтовой паре (здесь
приведенный угол трения <р' выбирают в зависимости от скорости скольжения
1
cos
cê
v
v
по табл.
5.7).
В каких расчетах [кроме формулы (5.14)] используется КПД червячной передачи?
§ 7. Последовательность проектировочного расчета червячных передач
5.20. Для закрытых и открытых червячных передач проектным является расчет на контактную
прочность.
Расчет зубьев червячного колеса на изгиб является проверочным за исключением открытых передач
при z
2
^ 80.
Исходные данные те же, что и в зубчатой передаче: передаваемая мощность Р, вращающий момент
Т, передаточное число и, угловые скорости валов червяка со, (частота вращения л,) и червячного колеса
со
2
(
n
i) ~~ Р
е
~ жим работы передачи.

Последовательность проектировочного расчета.
1. В зависимости от условий работы передачи и дополнительных требований задать скорость
скольжения и выбрать материал червяка и червячного колеса (зубчатого венца), рассчитать
допускаемые напряжения [ст]
я
и [a]
F
.
2. Определить передаточное число (или угловые скорости валов), а в зависимости от передаточного
числа выбрать число витков червяка Z
1
и число зубьев колеса z
2
. При этом принимают £
2
> 28.
3. Из условия ρ ≈ 0,25z
2
задать коэффициент диаметра червяка (ρ = 7,1 -f- 25 —
оптимальные пределы), коэффициенты К
&
, K
v
, КПД и по формуле (5.10) определить межосевое
расстояние из условия контактной прочности.
4. Определить модуль зацепления т и округлить его до ближайшего стандартного значения (см.
табл. 5.1).
5. В зависимости от полученного модуля т уточнить межосевое расстояние по формуле а = 0,5(ρ +
z
2
) округлив его до целого числа.
6. Произвести геометрический расчет передачи, найти d, d
a
, d
f
и другие размеры, определить ее
конструктивные элементы L, В, d
M1
(см. шаги 5.9 и 5.10).
Тело червяка проверяют на прочность и жесткость (см. расчет валов).
7. Из условия и
ск
= (0,015 ÷0,055)ω
1
, (м/с) вычислить скорость скольжения v
CK
и по табл. 5.7
определить угол трения.
8. Вычислить КПД передачи и сравнить его значение с предварительно принятым. При
значительных расхождениях произвести повторный расчет передачи.
9. По окончательно установленным параметрам передачи уточнить величину расчетной нагрузки,
определить фактические контактные напряжения и сравнить их с соответствующими допускаемыми
значениями (допускается недогрузка не более 10 % и перегрузка до 5 %).
10. Определить число зубьев эквивалентного колеса z
v
, по табл. 5.5 выбрать коэффициент формы
зуба Y
F
, по формуле (5.11) рассчитать фактические напряжения изгиба в зубьях колеса и сравнить их с
допускаемыми.
11. По формуле (5.13) провести тепловой расчет передачи.
5.22. Ответить на вопросы контрольной карточки 5.2.
Контрольная карточка 5.2
Вопрос Ответы
Код
Покажите формулу проектировочного
расчета на прочность силовой закрытой
червячной передачи
1
2
3
4
