Марчук Г.И., Лебедев В.И. Численные методы в теории переноса нейтронов
Подождите немного. Документ загружается.


длину на L в соответствии с направлением вектора ft. Тогда уравнение
(5.1.2) вдоль L запишется так:
/-^- +
<P
=
Q,
(9.6.1)
где
Q
= Q(<P,/,x,G) =
cS<p
+ /.
Уравнение (9.6.1)—обыкновенное дифференциальное уравнение,
заданное вдоль L. Пусть две точки Р
0
(£
0
)\ ^i (£i) € £> причем от-
резок [Р
0
> Pi] целиком принадлежит одной из замкнутых областей Dj,
и пусть h = ^i — io > 0. Введем обозначения:
/о
= /(Л)) = Пт /(©; h = f(PJ= lim /(£); т = А/(2/).
Класс функций
ср
(х, ft), являющихся ограниченными в Dj решениями
уравнения (5.1.2), обозначим^
1
(Z)
7
).
Пусть класс функций К}С
п
,ь1Рj)
определен^условием К}С
п
, a(Dj) = {q> :
q>
€ /С
1
(Dj), Q
(Ф,
/, х, ft) £
€ С
л
, a(Dj) для всех ft}, где п^ 0—целое число; а£ [0, 1]. Класс
Cn
t
a (Dj) определяется как класс функций, непрерывных в Dj, вместе
с частными производными до л-го порядка включительно, причем
последние удовлетворяют условию Липшица с показателем а.
Если считать Q известной функцией, то решение (9,6,1) на L при
Ъо
^ £ ^ li выражается формулой
Ф(8) =
Ф(*.
Й)-ехр(-(5-Ы/-
1
)ф
0
+ I'
1
fQexp((*-|)/-
1
)Л. (9.6.2)
Ь
Из формулы (9.6.2) следует, что если ф £ /С
1
^,» (А/), то ф £
£ C/24-i ,а ([^о» ^J)- Формула (9.6.2) обладает одним свойством, ко-
торое назовем монотонностью; оно заключается в том, что ф (х, ft)
является монотонно возрастающей функцией от ф
0
.
Предположим теперь, что функцию Q (I) можно хорошо аппрок-
симировать линейной функцией на отрезке [£
0
, gj:
Q (|) = /г
1
((I - i
0
) Q, + (1
г
- I) Q
0
) + О (АР), (9.6,3)
где P = 2 при n + a^2;P = n + a при n + a < 2.
Предполагая выполненным равенство (9.6.3) и вычисляя зна-
чение интеграла в формуле (9.6.2) при g = |
1э
получаем [пренебрегая
членом О (№+
1
))
Ф1 = РФо +
qQo
+ О - Р -
Я)
Qu (9.6,4)
где
р = exp (—ft//); (7 = 5 (й/0; Д (и) = 0 — ехр (—и))1и — exp (—а).
(9.6.5)
Построим разностную схему, позволяющую по ф
0
найти ф
х
. На
классе C
rt
,
a
([£<,» Ы) разностное уравнение (9.6.4) аппроксимирует
(9.6.1) с точностью О
(ДО).
Разностная схема (9,6.5) монотонна, так
210

как 0 < р < 1; легко также убедиться, что q > О, I — р — q ^ 0.
Уравнение (9.6.5) было предложено В. С. Владимировым в работе
[40];
в ней исследованы вопросы сходимости и точности решений
полученных разностных уравнений при h -^0. В формулах (9.6.5)
значения р, q можно приближенно вычислять, пользуясь дробно-
рациональными приближениями для ехр (—и) [см. формулы (9.6.14),
(9.6.17)].
В ряде задач, например в задачах со сферической и цилиндрической
симметриями, целесообразно учесть дополнительные сведения о ре-
шении, например симметричность или поведение искомых функций
в окрестности г = 0. Учет этих сведений приводит к представлению
функции Q на
[%
0
,
Ъ
х
] в виде
Q
= a?-b
a
)-4Q
1
(l
2
-^) +
Qo(l
1
2
-g
2
)].
(9.6.6)
Подставив (9.6.6) в (9.6.2), получим опять формулу типа (9.6.4).
Применим теперь метод конечных разностей непосредственно к
уравнению (9.6.1), что позволит получить некоторые дробно-линей-
ные приближения для коэффициентов формулы (9.6.4). Проинтегри-
руем уравнение (9.6.1) вдоль L по отрезку [Р
0
, PJ. Тогда
Si
/(<Pi—Фо) + f
<pdg
=
AQi/2,
(9.6.7)
I
где
h
Qi/2 = A"
1
JQ^. (9.6.8)
Рассмотрим один из способов аппроксимации интеграла
квадратурными формулами при условии, что ф £ К}С
п а
(Dj)
1119,
129].
Применим к / квадратуру Эйлера наивысшей алгебраической
степени точности
[101]:
'-(*.+*)т+-^Ш-(-*1)
+0(
*
,+ч
-
(96
'
9)
где
ГЗ при/г + а>3:
щ
(я + а при 0<я+а<3.
Значения производных в (9.6.9) выразим, пользуясь уравнением
(9.6.1),
через значения <р
ь
Q
it
В результате с точностью О
(/i
2
+
p
)
по-
лучим
/ = (<Pi + Фо) Л/2 + /i
2
(Q
0
- Qi +
Ф1
- Фо)/ (12 /). (9.6.11)
211

Теперь равенство (9.6.7) заменим с точностью О (Л
2
+Р) другим, про-
делывая следующие операции: разделим его на I, затем прибавим к
левой части член <т
0
тв
ф1> а к правой—член о^т
6
Q
1/2
, где положитель-
ные числа а
0
, а
г
выберем позднее; наконец, вместо / подставим выра-
жение (9.6.11). В результате получим
(1 + ог
0
т
в
) Фх — ф
0
+ т (ф
0
+ Фх) + т
2
(Q
0
— Qi + Фх — Фо)/3 =
= (2т + а^) Q
1/2
(9.6.12)
или __
Ф1
= «оФо + Ро Ql/2, (9.6.13)
где
а
0
= а (<т
0
, т) = (1 - т + т
2
/3) (1 + т + т
2
/3 +
^x
6
)-
1
;
(9.6.14)
Ро = т (1 + т + т
2
/3 + (Тот
8
)-
1
;
(
9
-
6
-
15
)
Qi/2 = (2 +
а
2
т
б
)
Q
1/2
+ т (Qx
—Q
0
)/3.
(9.6.16)
Схема (9.6.13) имеет точность локальной аппроксимации
0(h
l
+*),
где р задано формулой (9.6.10). Величины а
0
, а
2
выберем
так, чтобы схема (9.6.13) давала точное решение в случае, когда ре-
шением уравнения (9.6.1) является постоянная [т. е. когда
Q
= const
на (lo. £i) и ф = Q]. Подставляя в (9.6.12) значения Фх = Фо
=
Qi
=
— Qo
==
Q» получаем, что а
0
= а
х
= а, где а — любое положительное
число.
Осталось рассмотреть схему (9.6.13) на устойчивость и монотон-
ность. С этой целью исследуем поведение функции а (а, т).
Известно
[117],
что при а = 0 функция
а (0, т) = (1 — т + т
2
/3) (1 + т + т
2
/3)-
х
(9.6.17)
является подходящей дробью в разложении функции ехр (—2 т) в цеп-
ную дробь; при этом ехр (—2 т) <; а (0, т) ^ а (0,0) = 1 и
0 <1п (ехр (2т) а (0, т)) = О (т
б
) при т ->0. Таким образом, наиболее
простая при а = 0 схема (9.6.13) является устойчивой и монотонной
при любых т > 0, а а (0, т) достаточно точно аппроксимирует
ехр (—2т) при т ->0. Однако поведение функций ехр (—2 т) и а (0, т)
различно при т ->оо: если ехр (—2т) -^0, то а (0, т) ->1. Функция
а (0, т) при т = }/li имеет положительный минимум, равный
(7+41/3J"-
1
, да/дх < 0 при 0 < т < Уъ и да/дх > 0 при т > УК
Следовательно, для того чтобы решения разностных уравнений
(9.6.13) при а = 0 правильно сохраняли свойства решений уравнения
(9.6.1),
необходимо, чтобы 0<т<]/1Гили
h <
21/3/.
(9.6.18)
Чтобы избавиться от ограничения (9.6.18), распорядимся теперь
величиной а > 0; выберем ее так, чтобы а (а, т) наилучшим образом
приближала функцию ехр (—2т) при т > 0. Можно убедиться, что
при о > 0 будем иметь In (ехр(2т)а, (а, т)) =0 (т
б
). Это соотношение
получается разложением а (а, т) в ряд по степени т
4
Функция а (а, т)
212

является при т ->
оо
убывающей к нулю функцией, как т"
4
/а. Рас-
четы, проведенные с участием С. А. Фроловой, показали, что опти-
мальным значением является а = о
0
= 0,1304. При этом величина
tj = | ехр (—2т)
—
а (сг
0
, т) | не превышает 7,5 • 10~
б
при 0 < т <
^ 1,08 и max
TI
(т) < 9,8 • 10"
3
для остальных значений т. Таким
X
образом, при аппроксимации экспоненты в схемах (9.6.4), (9.6.13)
функцией а (ст
0
, т) достигается достаточная для многих задач точ-
ность и ограничений на шаг ft, связанных с аппроксимацией экспо-
ненты, не требуется.
Заметим, что если точки пересечения характеристики L
с
границами
областей Dj включить в число рассматриваемых пар точек (Р
ь
Р
0
), то
разностное уравнение (9.6.13) будет оставаться годным и для задач
с разрывными коэффициентами.
Получим теперь разностное уравнение для решения кинетического
уравнения, записанного в самосопряженной форме:
-[/
~Ju +
u
=
Q(u,
Р, х, ft), (9.6.19)
где
Q —
четная по ft функция.
Рассмотрим на характеристике L три точки P
t
(&), i = 0, 1, 2,
такие, что \
х
—
%
0
= g
a
—
li =
Л
> 0, а [Р
2
, Р
0
] £ Dj. Обозначим
8
2
u
i
=u
i+1
—2u
i
+u
i
_
1
\ <wi|S=-g-fi|+-^-(ii,
+1
+"!.!). (9.6.20)
Класс функций и (х, ft), являющихся ограниченными в Dj реше-
ниями уравнения (9.6.19), обозначим К
2
{Dj). Пусть /С
2
С„,
а
(D
7
)—
= {и; и б К
2
(Dj),
Q
(и, Р, *, ft) 6
С„.
а
(D
;
) для всех ft}. Из (9.6.19)
следует, что если и £ K
2
C
n
,a(Dj), то и g С
л+2
,а([Р
2
, Л>1).
Применяя способ построения разностных формул повышенной
точности
[119],
получаем, что для и £ К
2
С
п
,а
(Dj)
в точке Р
г
Шг"'
4
'"'-
-к
8
'(|г),
+0(П
(9
-
6
'
21)
где р = 4 при /г + а^4 ир = п + а при 0 < п + а < 4. Под-
ставляя в (9.6.21) значения д
2
и/д£
2
при
г
= 0, 1,2, из уравнения (9.6.19)
и пренебрегая членом О
(rfi)>
приходим к уравнению
—т
2
б
2
и
г
/4 +
(ои
г
=
coQj.
(9.6.22)
Перепишем его следующим образом:
—(3
—
т
2
) б
2
и
±
/(12
т
2
) + и
г
= coQx.
Из этой записи видим, что для того чтобы уравнение (9.6.22) правиль-
но отражало тип уравнения (9.6.19) (эллиптичность вдоль характе-
ристики L), необходимо выполнение неравенства (9.6.18). Очевидно,
213

что уравнением, аппроксимирующим (9.6.19)
с
меньшей точностью
и
не
требующим ограничений
на шаг,
является простое уравнение
— (llhf 64 + и
г
= Q
v
(9.6.23)
Опишем один
из
способов получения уравнения
для и на
границе
двух сред. Пусть
три
точки
P
t
(i = 0, 1, 2),
лежащие
на L,
располо-
жены следующим образом: точка
Р
х
лежит
на
границе_областей
D
n
, D
j2y
[P
l9
Р
0
]
6D
yi>
g
1
_g
0
=
ft
1
>0,
[P
2
, PJ
<E
D
J29
l
2
-
—
Ъг
=
h
2
>0. Запишем
для
отрезков
[P
2
> PJ
и
I^i» Pol
П
Р
И
±
й
уравнение (9.6.13).
В
полученной таким образом системе четырех
уравнений перейдем
по
формулам (5.1.13), (5.1.14)
к
функциям
и
и
v
iy
t
=
0,
1,2, а
затем исключим
из
преобразованных уравнений функции
Vu
i = 0, 1, 2; в
результате этой операции получим одно уравне-
ние,
связывающее
и
0>
и
ъ
и
2
.
Уравнения (9.6.4), (9.6.13), (9.6.22), (9.6.23) послужат
нам
осно-
вой
для
построения систем разностных уравнений, аппроксимирующих
краевые задачи переноса.
Они
достаточно точны,
что
является нема-
ловажным обстоятельством
при
решении многомерных задач,
в ко-
торых всегда желательно снизить общее число расчетных узлов сетки.
Сходимость
при
измельчении сетки решений разностных уравнений
метода характеристик
к
точному решению доказывается путем
ис-
пользования свойств монотонности разностных схем
и
энергетических
неравенств, полученных
из
разностного аналога интегрального соот-
ношения (5.1.11).
При решении методом характеристик многомерных задач
при до-
статочно густой пространственно-угловой сетке требуется проводить
два типа продолжения функций: интерполяцию
в
расчетные точки
характеристик значений функции
Q,
заданной
на
некоторой сетке
D
hy
и разнос значений
ср
(х,
й),
рассчитываемых
на
характеристиках, в точ-
ки
D
h
для
образования значений функции
Q. Для
одномерных задач
эти трудности
не
возникают.
§ 9.7. ПОСТРОЕНИЕ СЕТКИ И РАЗНОСТНАЯ
АППРОКСИМАЦИЯ КИНЕТИЧЕСКОГО УРАВНЕНИЯ
ДЛЯ ЦИЛИНДРИЧЕСКИ-СИММЕТРИЧНЫХ ОБЛАСТЕЙ
(БЕСКОНЕЧНЫЙ ЦИЛИНДР)
Пусть
R
3
(х, у, z) —
трехмерное пространство. Получим системы
разностных уравнений, аппроксимирующих уравнение
/ЙУФ
+ Ф = Q (9.7.1)
в области
D,
являющейся бесконечным цилиндром:
D= {{x,y,z):x*
+
y*<R
2
}.
Пусть
Q
= -^ JO +
3jiQQ')cp(x, Q')dQ'
+ f
0
+
3costysm$f
ly
(9.7.2)
Q
214
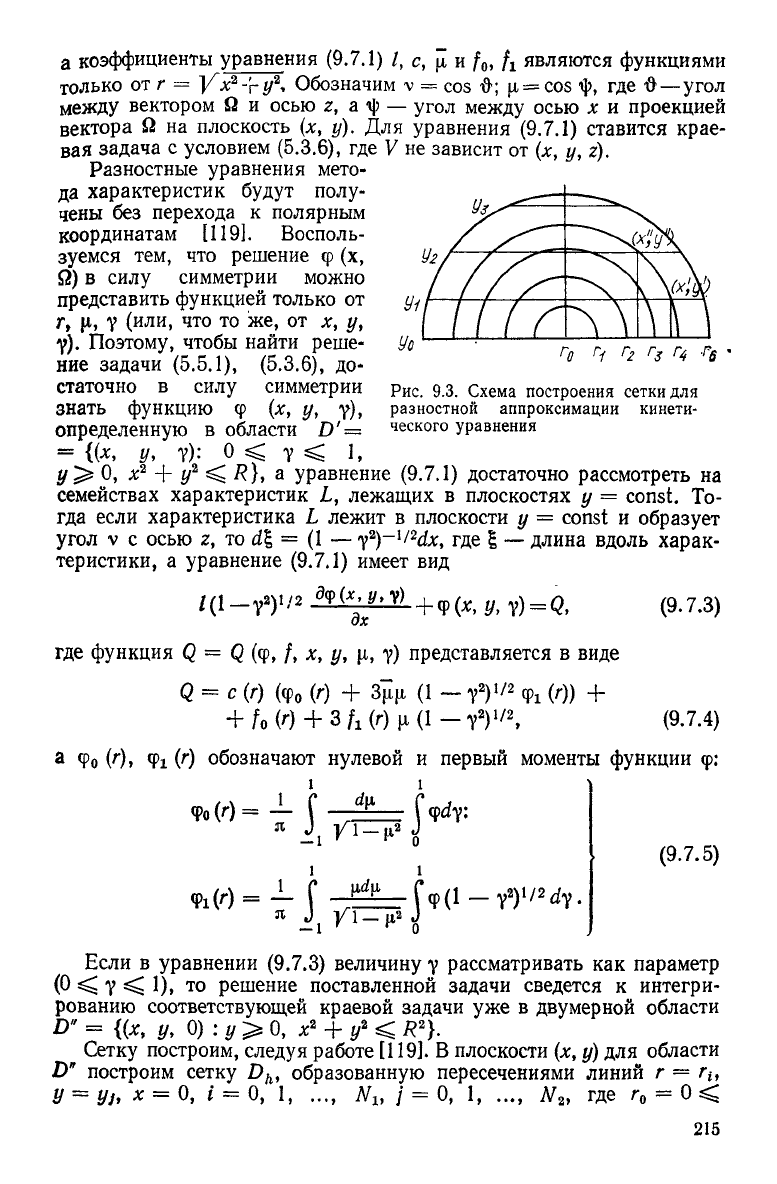
Гг
r
s
r
4
Рис. 9.3. Схема построения сетки для
разностной аппроксимации кинети-
ческого уравнения
а коэффициенты уравнения (9.7.1) /, с, JI и /
0
, /
х
являются функциями
только от г =
]^х
2
-'
г
у
2
*
Обозначим v = cos ft;
(i
=
cos
ф, где Ф—угол
между вектором Q и осью z, a i|)
—
угол между осью л: и проекцией
вектора Q на плоскость (л;, */). Для уравнения (9.7.1) ставится крае-
вая задача с условием (5.3.6), где V не зависит от (х, у, z).
Разностные уравнения мето-
да характеристик будут полу-
чены без перехода к полярным
координатам
[119].
Восполь-
зуемся тем, что решение ф (х,
Q)
в силу симметрии можно
представить функцией только от
г, у,
Y
(
или
>
что то же
>
от
*•
У*
у).
Поэтому, чтобы найти реше-
ние задачи (5.5.1), (5.3.6), до-
статочно в силу симметрии
знать функцию <р (#, у, у),
определенную в области
D'
=
= {(*, у, у): 0 < у < 1,
у^
О,
х
2
+ у
2
< R}, а уравнение (9.7.1) достаточно рассмотреть на
семействах характеристик L, лежащих в плоскостях у = const. То-
гда если характеристика L лежит в плоскости у = const и образует
угол v с осью z, то d\ = (1
—
y
2
)~
l
l
2
dx,
где \ — длина вдоль харак-
теристики, а уравнение (9.7.1) имеет вид
/(
l_
Y
2)i
/2
fo^F'fl+yfr у,
T
) =
Q,
(9.7.3)
где функция Q =
Q
(Ф,
/, #, г/, ц, -у) представляется в виде
Q = с W (Фо (г) + ЗЙ1 (1 - 7
2
)
1/2
Ф1
W) +
+ fo(/') + 3/
1
(r)
t
x(l-Y
2
)
1
/
2
, (9.7.4)
а
Фо
(
г
)>
Ф1
(
г
) обозначают нулевой и первый моменты функции ф:
(9.7.5)
Если в уравнении (9.7.3) величину у рассматривать как параметр
(О
< у < 1), то решение поставленной задачи сведется к интегри-
рованию соответствующей краевой задачи уже в двумерной области
D"
= {(*, у, 0):у^
О,
х
2
+ у
2
< Я
2
}.
Сетку построим, следуя работе
[119].
В
плоскости
(х,
у)
для области
D"
построим сетку D
h
, образованную пересечениями линий г = г
и
у = у
и
х = 0, i = 0, 1, ..., Ы
ъ
j = О, 1, ..., N
29
где г
0
= 0 <
215

<ri-i<r
t
<r
Nl
=
R>
i=U 2, ..., tfi; y
0
= 0 < y^
x
<
*/
7
-
<
< .ttv, </?,/ = 1, 2, ..., ЛГ
2
(рис. 9.3).
В разбиение
{г*}
включим все границы областей D
7
-, являющихся
концентрическими кольцами, внутри которых предполагаем постоян-
ными функции I (г), с (г),
~\i
(г), /
0
(г), /
х
(г). Разбиения {г
г
}
±
{yj}
выбраны независимыми друг от_друга. Пусть
r
OJl
r
xj
(r
oj
< r
xj
) —
границы Dj, тогда сетку
по г для
Dj, состоящую из
п
}
-
+
1
точки, целе-
сообразно выбрать в виде r\\ =
r%\
+ (г?/
— гЦ)
(sin -^j (k =
= 0,1, ..., Л/), где m = 1 при 7
и
= Я, и = 1, V = 0 и/п = 2восталь-
ных случаях.
Для заданного целого N
3
> 0 из всех значений
Y
рассмотрим та-
кие у = 7ft,
&
= 1, 2, ...,
N
3
>
которые являются положительными
корнями многочлена Лежандра степени 2N
3
; тогда 0<Yft<l.
Целесообразность такого выбора разбиения {у
к
} будет показана при
оценке ошибки квадратуры по у для вычисления функции ф
0
(г).
Пусть Р
0
(х
0
, у^), Р
г
(лг
1э
yj) —две соседние точки сетки D
h
, ле-
жащие на прямой у = yj, a h = х
х
—
х
0
> 0. Тогда в уравнении
(9.6.13) для этих точек и в величинах а
0
, р, Q
1/2
[см. (9.6.14) —
(9.6.16)] следует считать
т =
2/(1—
V
2)l/2
;
(Го
= 0,1304; Qi/2^"
1
I Qd*.
*о
Теперь осталось получить удобную квадратуру для Q
x
/^ В нашем
случае
*§Qdx
= с(J<podx+3vL(l - ?
2
)
1
/
2
]^Ф1^)+/оЛ + 3/
1
(1-7
2
)
1/2
^
Х
0
\Х
0
Х
0
I
где Дг = г
х
—
г
0
;
r
%
- Vxf + yf, i = 0, 1.
Пусть ф
а
(г) £
С„,
а
([г
0
, г
х
]), где
1
< п < 3.
Тогда
*о
Го
-(^-)J + 0(|Ar|P+'), (9.7.6)
где Уи = cpi (r
f
), i = 0, 1, р = п + а. Заметим, что функции ф
0
,
Ф
х
связаны между собой дифференциальным уравнением баланса
7--|-(пй)
+ (1-с)Фо =
/в.
(9.7.7)
Находя
dtfx/dr
из (9.7.7) и подставляя это соотношение в (9.7.6), по-
лучаем на классе
С„,
а
([r
0
, rj) с точностью О (| Дг | )*И квадратур-
216

ную формулу
х
1
Wi
dx=
-у-
(Фи
+
Фю)
+
(Аг)
2
[Фи
Т
г
—
Фю
Го
х
+
I
*0
+
(1
—с)
/-
1
(Фо1—Фоо)]/12. (9.7.8)
Из набора квадратур
для J
ф
0
^л; выберем такие, коэффициенты
х
0
которых есть дробно-рациональные функции
от
координат точек
Р
0
,
Р
г
невысокой степени. Тогда мы будем избавлены от необходимости
табулирования некоторых трансцендентных функций. Очевидно,
что
вид квадратурных формул зависит от характера продолжения функции
ф (*> У
у
?)> заданной на
D
h
,
на всю область
D'.
Предположим, что по
у
функция
ф
(А:,
у, у)
продолжается четным многочленом Лагранжа сте-
пени
2N
3
,
построенным
по
точкам y
k
,
k = 1, ..., N
s
, и
что значения
функции
ф (0, y
h
у)
продолжаются
на
точки
(0, г
и
у)
квадратичной
интерполяцией.
Остановимся
на
двух типах продолжения
для
функции
ф
0
(г).
Сначала предположим, что функция ф
0
(г) может быть хорошо прибли-
жена между двумя соседними точками
г
0
, г
г
(г
0
,
г
г
£
{г*}) формулой
вида
с
г
+
с
2
г
2
.
Такой
вид
продолжения согласуется
с
поведением
гладких функций
ф
0
(г)
при
г = 0.
Тогда при
г
0
< г ^ г
г
Фо
(г)
=
(Аг
2
)"
1
(фоо
(П -г
2
)
+
Фо1
(г
2
-г
2
)), (9.7.9)
где фо*
=
Фо (П),
i = 0, 1,
Ar
2
= r\
—
r\.
Прежде чем перейти
к
выводу квадратуры для
ф
0
,
следует заме-
тить,
что в
разбираемой задаче шаг
по
характеристике Ах
=
х
г
—х
0
может быть величиной
О (|
Аг|
1
/
2
). Поэтому если ошибка локальной
аппроксимации
в
формуле (9.6.9) есть
О
(ft
a
),
то
интеграл
J
q>
0
dx
х
0
достаточно аппроксимировать
с
точностью
О
[(Ar)
a
/
2
].
Считая,
что
функция
фо
(VI) £
С
п
,
a
(Irl,
г\]) и что
она может быть приближена
по формуле (9.7.9), получаем
L
0
dx= Г »('>'* ^Л^ +
ОИАхиЬПгь
+ г^Щ, (9.7.10)
Х
0
Г
0
где Рх
= min (2, п + а);
У
(<Ро) =
о
/^ .
«
2
*i
+ *о)
Фоо
+ (2*о + *i) Фи). (9.7.11)
3(*i+*o)
Можно предположить другое продолжение, отражающее специфи-
ку решений кинетического уравнения. Предположим, что ф
0
(г) между
точками
г
0
, г
г
является решением Р
2п-1
-уравнений сферических гар-
моник
или
Р^/-уравнений
(см. гл. 8),
принимающим заданные зна-
чения на концах отрезка [г
0
,
г
г
].
Идя по такому пути, можно получить
продолжения, мало отличающиеся
от
истинных значений функции
Фо(г).
Проиллюстрируем этот прием на простейшем примере продол-
217

жения
с
использованием Р
г
уравнений метода сферических гармоник.
Пусть функция
фо (г)
удовлетворяет уравнению
3r dr \(1 -fxc) dr Г
к ;Y0 /0
r dr \
1
— |*c ]
V
при
r
0
< r < r
x
И
ф
0
(г
0
)
=
Фоо,_Фо (>i)
=
Фо-
Считая
в
(9.7.12) величины
/, |л, с, /
0
, /i
постоянными, можно было
бы точно найти решение этой задачи,
но оно,
однако, оказалось
бы
неудобным
для
квадратурных формул,
так как
содержит функции
Бесселя. Поэтому будем искать приближенное решение (9.7.12)
в
виде
Фо (г)
=
(Дг
2
)-1 [(г?
-г
2
)
ф
00
+
(г
2
—г§)
Фо1
+ р (г*-гЪ)
(л?
-г
2
)],
(9.7.13)
где постоянную Ъ определим из требования, чтобы для функции
ф
0
, заданной формулой (9.7.13), было выполнено уравнение баланса
+ (1-с)?ф
0
г£1г = /в4г-
А
^. (9.7.14)
J
2
1
—
ис
Го
г
Подставляя (9.7.13)
в
(9.7.14), получаем
ь
_^
А;*[/о—(1—
с)(фоо+фо1)/2] + р[фо1
—
Фоо—ЗДАГ/^/)]
(97 15)
(1—c)(Ar»)V6+p(rJ + rJ) '
где
р = 4
/
2
/(3 (1
—
\ic)).
В
этом случае квадратурная формула
имеет
вид
*
Фо^=
=
У(фо)
+
2(А
"
)2(Х12+
"
2о+3
^
1
^
о)6
> (9.7.16)
J '" ""' ' 15(*i+*
0
)
Хо
Применение последней квадратурной формулы должно улучшать
некоторые разностные соотношения, соответствующие точному урав-
нению баланса нейтронов,
а
также ускорять сходимость итерацион-
ных методов,
так
как формула (9.7.16) предполагает, что для заданных
значений
/
0
, f
x
и для
любых начальных приближений
для
значений
Фо
(
r
i)
всегда выполнен баланс нейтронов
на
отрезке
[r
0
, г
г
].
Объединяя формулы (9.7.8), (9.7.10)
или
(9.7.16), получаем квад-
ратуру ДЛЯ
Qi/2.
Функцию
ф
х
(г)
определяем
на
множествах
{r
t
}
9
{yj}
через про-
должение
фо (г),
пользуясь уравнением баланса (9.7.7):
l{ri<hfi)-r7<h<ro)) + (\-c)§
4>
0
rdr
=
f
0
rf
~
rg
, (9.7.17)
r~
0
где
ф
х
(0) = 0, а г
ъ
г
0
—
две соседние точки
из
упорядоченного набора
D'H
точек
{rj (r
i+1
^ г*),
составленного
из
всех точек
{rj, {yj}.
218

При а = 0 на величину шага h следует наложить ограничение
(9.6.18),
которое будет иметь вид
h <
2
УЗ Imin
(1 —
у!)
1
/\ (9.7.18)
а поскольку h
2
< | Ar | (r
0
+ /*i) и min ]Л — у| > 3/(2 (2Л^
3
+ 1))
/г
(см.
[210]), (9.7.18) будет выполнено при условии
|АГ|<27/
2
(2Л/
3
+1Г
2
(А-
1
+ /'О)-
1
.
§ 9.8. КВАДРАТУРНЫЕ ФОРМУЛЫ В МЕТОДЕ ХАРАКТЕРИСТИК
ДЛЯ ИНТЕГРАЛЬНЫХ ОПЕРАТОРОВ
В ЦИЛИНДРИЧЕСКИ-СИММЕТРИЧНЫХ ГЕОМЕТРИЯХ
В обозначениях §9.7 нулевой и первый моменты от решения, под-
лежащие замене квадратурными формулами, выразятся для цилин-
дрически-симметричных задач формулами (9.7.5). Пусть D
h
— сетка,
Ф (
х
> У у
У)
— решение (9.7.1), а
1
J
(*>У)
= j
Ф
(*>
У
у У)
dy.
Легко убедиться в том, что нулевой момент ф
0
(г)
при 0 < г < R можно,
используя симметрию решения задачи, выразить формулой
Фо
(0 = — \ J
(г cos
ij?, г sin
i|))
do|).
(9.8.1)
о
Получим квадратуру_для ф
0
(г), используя лишь узлы сетки D
h
[129].
Для этого положим J (х, у) = J (х, у) + J
(—х
9
у).
При г = г
0
= 0 на основании (9.8.1) имеем точную формулу
Фо (0) = / (0, 0). (9.8.2)
Теперь получим квадратурные формулы при г < у
2
(для радиусов
г
ь
г
2
на рис. 9.3). Воспользуемся тем, что функция J (г cos of, г sin г|э)
вследствие осевой симметрии, если она гладкая, слабо зависит от
я|э
при малых г. Представим функцию J в виде суммы четной и нечетной
функций по г|э относительно я/2:
J (г cos
1]),
г sin ф) = /
х
(г, г|)) + /
а
(г, г|>), (9.8.3)
где
А (Л Ф) = h (', я - if); У
а
(г, ф) = - /» (г, я -
<|)).
(9.8.4)
Тогда согласно (9.8.1)
Фо(/•)
= — f
Ji{r,*)d*.
(9.8.5)
о
219
