Малыхин В.И. Математика в экономике
Подождите немного. Документ загружается.


1)
умножение
или
деление одного
из
уравнений
на
число,
не
равное
0;
2)
прибавление
к
одному
из
уравнений другого уравнения.
Утверждение. Эквивалентные
преобразования
СЛАУ,
даже
выполненные
последовательно
любое
число
раз,
дают
СЛАУ,
экви-
валентную
исходной.
.
Для
решения СЛАУ часто используется широко известный
ме-
тод
последовательного исключения неизвестных
или его
модифика-
ция
— так
называемый метод Жордана-Гаусса. Суть этого
метода
состоит
в
том,
что
СЛАУ,
скажем, 3-го порядка элементарными пре-
образованиями
приводится
к
виду, который называется треугольным
или
трапециевидным.
a'
n
x
l
+ti
r
]2
x
2
+^
n
x
3
~l)'
lf
-
"22*2
"*"
23
Х
3
"^
2'
(/33*3
-Й'
3
.
Решение этой системы (эквивалентной исходной) найти легко.
Оно
будет,
следовательно,
и
решением исходной СЛАУ.
Пример
I.
Решить СЛАУ
методом
Жордана-Гаусса:
jc,
+*
2
-Кх
3
=6,
•
АД.
^"л^
^^м
^"3г
•
2*
2
-*
3
«1.
Решение
вручную
оформляют
в
виде
специальных
таблиц,
но
делать
так не
обязательно. Суть метода
— в
последовательном
исключении
неизве-
стных.
На
1-м
шаге
исключим
х.
из
всех
уравнений,-кроме
первого;
о
я,
-\-х
2
+х
3
-6,
•
*"*
«JA.
^
Xj
~~*~*s
t
АЛ
2
"^
Л\
^
1,
На 2-м
шаге исключим
х
а
из
всех
уравнений, кроме второго:
1
~~
ч
">
"~
-ЗЛ-
~™
А-
~"'1
5х
2
^Ю.
22

23
На
3-м
шаге исключим
х
г
из
всех
уравнений, кроме
третьего:
х,
=1,
-*з
=
-
3
>
5х
2
=
10.
Но
решение этой СЛАУ очевидно:
х,
=
I,
х
г
=
2,
х
3
= 3.
3.
Определитель
матрицы.
Пусть
А=\
п
12
—
квадратная
(
°21
а
22
I
матрица
2-го порядка.
Определителем
матрицы
А
называется число
а
\\
а
\2
°и
й
22
~
°12
а
2г
Определитель обозначается
Д(Л)
или
а а
.
Опре-
делитель матрицы 3-го порядка
4i
a
i2
а
\з
'
Л=
U
2
1
Д
22
Д
23
,«31
Л
32
«33
,
вычисляется
так;
Д(^)
=
а
и
а
21
а
33
+
Д
12
а
23
й
31
+
а
13
^
2|
й
32
-
а
13
о
гг
а
31
-
"
e
i2
e
«
e
as
~
в
и
л
аз
в
зг
Минором
некоторого элемента определителя называется опре-
делитель, получаемый
изданного
определителя вычеркиванием стро-
ки
и
столбца,
на
пересечении которых расположен
этот
элемент. Так,
минором
элемента
в„
вышенаписанного определителя 3-го порядка
является
определитель
Д.,
=
22>
23
.
11
°32
"33
Алгебраическим дополнением
некоторого
элемента
определителя
называется
минор
этого
элемента, умноженный
на
(-1К
где s —
сумма
номеров строки
и
столбца,
на
пересечении которых располо-
жен
этот элемент.
Свойства определителей:
1)
определитель
не
изменится
при
замене строк
столбцами,
т.е.
определитель транспонированной матрицы равен определи-
телю исходной матрицы;
2)
перестановка двух строк (столбцов) определителя равносиль-
на
умножению
его на
минус единицу;
3)
если определитель имеет
две
одинаковые строки (столбца),
то он
равен нулю;

4)
общий множитель элементов
строки
(столбца) можно выне-
сти
за
знак определителя;
5)
определитель
не
изменится,
если
к
элементам одной строки
(столбца)
прибавить соответствующие элементы другой
стро-
ки
(столбца),
умноженные
на
одно
и то же
число;
6)
определитель равен сумме произведений элементов какой-
нибудь
строки (столбца), например
/'-и,
на их
алгебраичес-
кие
дополнения,
т.е.
Л(Л)
=
а
п
А
п
+...
+
а,
п
А
1п
или
Д(Л)
=
п
—
£<?#/!#,
где
A
lk
—
алгебраические Дополнения
элемен-
*«i
TOBfl,,.
Эти
свойства
позволяют
найти определитель любой квадратной
Матрицы.
Однако
нахождение
определителя,
например, 5-го порядка
вручную
довольно трудоемко.
При
необходимости нужно воспользо-
ваться компьютерными программами.
Мы
ограничимся
только
оп-
ределителями
не
выше 4-го порядка.
1234
1231
Пример
2.
Вычислить
определитель
4-го
порядка;
Д-
* *
.
2341
Решение,
Раскладываем
определитель
по
элементам
1-й
строки:
А
=
1Д„
-
2Д
13
+
ЗД
П
-
4Д
]4
.
Находим
Д,,,
Д
|2
,
Д,
э
,
Д
14
.
Это все
определители
З^го
порядка.
Найдем,
к
примеру,
Д„:
д
в2
1 0
.
1 0
,
,[1
1
«2-3+
1
aft
»
4131
'|3
4
°'
Так
же
находим
Д
|3
=
-I,
Д
|3
=
-1,
Д
н
=
-I,
Окончательно
Д « 3.
4.
Решение
СЛАУ
с
помощью определителей.
Рассмотрим
СЛАУ
из
трех уравнений
с
тремя неизвестными:
Л1|*1+вИ*2+«И*
3
в
*р
в
21*1
+
в22*а
+
«23*3
аа
*2*
«31*1
•
|
"
Й
32*2
+«33^3
=Л
3'
а
\\
Д
12
<*,}
b
lm
a
l2
«
13
в
и
6,
а
13
Пусть
д
=
я
21
а
п
а
п
,
А,
*
Ь
г
а
п
я
23
,
д
2
=
Й21
А
2
я
2
з
>
а
з\
а
зг
°зз
А
з
°32
я
зз
й
3[
6
3
а
33
б
п
й,
2
И,
Дз^
°2i
^22
ь
г
•
а
31
Й
32
Й
3
24

Тогда,
если
Д
^
0, то
СЛАУ имеет единственное решение (формулы
Крамера):
я,
-
д,/Д,
х
2
-
Д
2
/Д,
х
3
=
Д
3
/Д.
Отметим,
что.аналогичные
формулы применяются
для
решения
любых
СЛАУ,
в
которых число уравнений равно числу неизвестных
и
определитель матрицы
из
коэффициентов
при
неизвестных
не ра-
вен
нулю.
Пример
3.
Решить
СЛАУ
по
формулам Крамера:
х,
+2*
2
-+Зх
3
-14,
х
2
+Х
3
=5,
2х,
+3х
2
+4х
3
=20.
Ответ;
*,
=
-1/-1
=
1,
л,
=
-2/-1
=
2,
х
3
=
-3/-1
=
3.
5.
Обратная матрица. Пусть
А —
какая-нибудь матрица. Тогда
матрица
В
называется обратной
к
ней, если
АВ =
ВА
=
Е,
где Е —
некоторая единичная матрица.
Весьма прозрачная аналогия
с
числами:
для
числа
2
число
1/2
есть обратное,
так как 2
-1/2
~
1.
Именно поэтому
матрица,
обрат-
ная
к
А>
обозначается
А~
1
.
Предложение.
Только квадратная
матрица
может
иметь обратную,
Доказательство.
Как
известно,
единичная
матрица
—
матрица квад-
ратная, пусть
Е
имеет
s
строк
И
столько
же
столбцов.
Пусть
матрица
А
имеет
размеры
/их
л,
а
матрица
В —
kxt.
Тогда
из
того,
что АВ - Е
вытекает:
т
»
s
t
п
-
А,
а из
того,
что ВА
«
Е
вытекает:
k
«
m,
t - s.
Следовательно,
т
«
k
B
/i,
что и
требовалось
доказать (еще получаем;
k -
/
-
/н
=
л,
т.е.
/I
И В —
квадратные
матрицы).
Для
нахождения
обратной матрицы можно использовать следу-
ющий
алгоритм (исходная матрица обозначена
А):
0)
смотрим, квадратная
ли
матрица; если
нет,
обратной
матри-
цы
не
существует; если квадратная, переходим
к п, 1;
1)
вычисляем определитель
Д(Л);
если
он
равен
нулю,
обратной
матрицы
не
существует; если
он не
равен нулю, переходим
к
п. 2;
2)
вместо каждого элемента матрицы ставим
его
алгебраичес-
кое
дополнение;
3)
полученную матрицу транспонируем;
4)
каждый элемент полученной матрицы делим
на
определи-
тель исходной матрицы
Д(/1)
и
получаем матрицу, обратную
данной,
Прим
ер
4.
Пусть
А-\
\
\
},
Определитель
Д(/1)
»
I,
значит,
обратная
\
•*
*)
матрица
существует,
Ставим
вместо
каждого
элемента
его
алгебраическое
25

/2
_з
\
дополнение, получаем
матрицу
,
0
.
Транспонируем
и
делим
на
Д(Л)
= 1.
\~i
г
j
I
2
-IV
Матрица
А~
1
~\
ч
о
—
обратная
к
/1.
у—->
^
у
/2
IV 2
-П_М
0]
Проверка:^
2
Д_
3
2
j-[
0
1
J-
Обратная
матрица полезна
во
многих ситуациях.
Пример
5.
Решим,
например,
матричное
уравнение
АХ
=
В,
где
/1
"f?'!'-
s
~(ior
Мы
только
что
нашли
матрицу
Л~',
обратную
к
мат-
(32}
\ 1 2 I
рице
А,
Умножим
наше
уравнение
слева
на
матрицу
Л"':
А~
1
АХ
=
А~*В.
Но
17-2}
А~
1
А
=
E
t
значит,
Х=
А~*В.
Итак,
решение
уравнения
есть
матрица
_до
4 г
"~-
№о-4
2
Н?
2
°}
Находить
обратную матрицу
к
матрице большой размерности
весьма
трудоемко.-Надо
обязательно
использовать
компьютер.
При
этом,
тем не
менее, остается трудность ввода
в
компьютер элементов
самой матрицы.
Представим,
что
надо
ввести
в
компьютер матрицу
из
100
строк
и
100
столбцов.
Это 10 000
элементов.
Если
эти
элемен-
ты
есть числа вида
36, 23,
т.е.
два
знака
до
запятой
и два
после
запя-
той,
да еще
сама запятая,
то
надо ввести
50 000
знаков. Если
на
каж-
дый
знак
тратить
I с
(надо ведь работать надежно,
без
ошибок!),
то
для
ввода понадобится
50000
;
3600,
т.е.
примерно
16
ч.
ЗАДАЧИ
x
l
+
a#
2
-U
1.
Найти
все а, при
каждом
из
которых
СЛАУ
,
__
з
(XX|
'Х
1
)
""ОС
несовместна, неопределенна,
определенна,
совместна.
Решение. Выразим
я,
из
первого уравнения
и
подставим
во
вто-
рое.
Получим
уже
одно
уравнение:
(1 -
а?)х
2
=
а
2
~
а.
Если
а
^
±1,
то
это
уравнение
имеет единственное решение
х
2
=
-а/(1
+ а) и
система
тоже имеет
единственное-
решение
x
l
=
(I
+
а +
а
2
)/(1
+ а),
х
2
«
-а/(1
+ а).
Если
же а -
±1,
то
случаи
а - 1 и а
=
-I
надо
исследовать
особо.
При а
=
1
получаем,
что
уравнение
(1 -
а?)х
2
=
~
а
2
- а
имеет
бесконечно много решений
—
каждое число есть
его
решение. Значит,
и
система
имеет
бесконечно много решений.
При
а - -1
уравнение
(1 -
а?)х
2
-
а
2
- а
не
имеет
решений, значит,
и
система
не
имеет решений.
Итак,
окончательно получаем: СЛАУ
нс-
26

27
совместна
при
а -
—1,
неопределенна
при
а - 1,
определенна
при
а
?*
±1 и
совместна
при
ос
ч*
-1.
2.
Введите необходимые векторы
и
матрицу
и
запишите СЛАУ
в
векторном
и
матрично-векторном
виде:
^А°2
—Х\
"""^3
~">
Лт
—о
~rX\
~'X')
t
л
г
-10+^3=0.
3.
Последовательно исключая
неизвестные,
приведите СЛАУ
к
треугольному виду
и
найдите
ее
решение:
X1
'Х>)
"""Jfi
~Ч,
2^С
i
*~Xj
'Хъ
~~
—
1)
4x,
-*
2
=].
4.
Решите СЛАУ
по
формулам Крамера:
лХ
\
~~"Х-у
"""Лт
~~U)
X
\
т
л
2
*•*
л
1
*™
'»
JA
I
~"
A
2
A
2
"~*
1
•
5. При
каком соотношении параметров
д,
£,
с
матрица
не
имеет
обратной?
Укажите хотя
бы
одну
тройку параметров, чтобы матрица
не
имела
обратной:
/
1 1 \
а
)
1
1
b \ .
\\ 1 с)
6.
Для
каждой
из
данных матриц найдите обратную:
(10)
(41)
(я
т] 1
Ц'
\02)>(02J'\Q
I
j'
^^'
7.
Вычислите определитель квадратной матрицы
«-го
порядка,
у
которой
на
главной диагонали
стоит
число
п.
Указание.
Используйте
индукцию.
8.
Можно доказать,
что
определитель произведения квадратных
матриц
равен произведению определителей. Проверьте
это для
мат-
рицы
N
0
,
возведенной
в
квадрат,
в
куб.
\
^
*•
I

Тема
И,
ЛИНИИ
НА
ПЛОСКОСТИ
И В
ПРОСТРАНСТВЕ
Основные
сведения
о
системе координат
на
прямой
и о
пря-
моугольной
системе координат
на
плоскости
и в
пространстве счи-
таются известными. Считаются известными также
осноцные
сведе-
ния
о
свободных
векторах
(«свободных
направленных
отрезках»),
28
9.
Выведите
из
предыдущей задачи,
что
определитель обратной
матрицы
(если
она
существует)
есть
число,
обратное
к
определителю
исходной
матрицы.
Указание.
Докажите,
что
определитель единичной матрицы равен
1.
10.
Докажите,
что
если
СЛАУ имеет хотя
бы два
решения,
то
решений
у нее
бесконечно много.
11.
СЛАУ называется
однородной,
если
все
свободные
члены
равны
нулю.
Докажите,
что
если такая СЛАУ имеет ненулевое реше-
ние,
то
решений
у нее
бесконечно много.
12.
Найдите матрицу, задающую линейное преобразование
R
2
в
себя, переводящее вектор
п
в I , , а
вектор
i
в
*
.
V
u
/
V
1
/
.
\
1
I
\*}
Указание.
Решите
матричное уравнение
ХА
=
Б,
где
X—
искомая
матрица,
л4\
}!*-(?
2
1
\\J
I
J
\
I
Z
/
13.
Пусть
ос,
{5
—
линейные преобразования пространства
R\
заданные
матрицами
А,
В,
Если
их
выполнить
последовательно,
одно
за
другим,
то
результирующее преобразование задается матрицей-
произведением
(в том же
порядке).
Найдите
матрицу, осуществляю-
щую
преобразование
а •
р,
р • а,
14.
Докажите,
что в
пространстве
R
2
любые
два
непропорцио-
нальных
вектора образуют базис.
15.
Докажите,
что в
пространстве двух товаров любой набор
может быть получен
в
виде комбинации
оЛГ+
рКдвух
непропорци-
ональных
наборов товаров, однако
не
всегда
коэффициенты
а, Р
будут неотрицательными.
Указание. Используйте
предыдущую
задачу.

о
связи координат точки
с
проекциями
ее
радиус-вектора
и
некото-
рые
подобные сведения.
2.1.
ПРЯМЫЕ ЛИНИИ
НА
ПЛОСКОСТИ.
ПЛОСКОСТИ
И
ПРЯМЫЕ ЛИНИИ
В
ПРОСТРАНСТВЕ
1.
Прямая линия
на
плоскости,
различные
виды
уравнений
пря-
мой.
Пусть точка
0(0,
0)
есть начало
координат,
точка
пересечения
горизонтальной
ОХ
и
вертикальной
ОУосеЙ
координат
(рис.
1). На
этих осях фиксированы единицы дли-
ны,
обозначенные отрезками
ОЛ/,
ON.
На
горизонтальной оси, направленной
вправо,
будем откладывать координату
х, на
вертикальной,
направленной
вверх,
координату
у. На
рисунке
на
плоскости нанесены различные точки.
Уравнением
линии
на
плоскости
на-
зывается равенство
F(x
t
у) - 0,
кото-
рому удовлетворяют координаты
лю-
бой
точки, принадлежащей
этой
ли-
нии,
и не
удовлетворяют координаты
любой точки,
не
принадлежащей
этой
линии.
Известно,
что
любое линейное уравнение
с
двумя переменными
ах
-ь
by - с
определяет прямую линию
на
плоскости. Покажем,
как
наиболее
рационально строить прямые
линии,
заданные линейными
уравнениями
разного
вида,
Например,
требуется построить
прямую
по
точкам пересечения
ее
с
осями координат.
Так
удобно
строить
прямую,
заданную
уравне-
нием
ах
+
by
=
с,
например
2.Y
+
Зу
~
6.
Действительно,
для
нахож-
дения точки
пересечения
этой прямой
с
осью
ОХ
надо
положить
29

У
=
о,
получим
х
-
3,
т.е.
точку
А
(рис.
2, а).
Аналогично,
для
нахож-
дения точки пересечения
с
осью
OY
надо положить
х
=
0,
получим
у -
2,
т.е. точку
В.
Через
эти две
точки
и
проводим искомую
прямую
/.
Это же
уравнение
можно
переписать так:
х/3
+ у/1 = 6.
Такой
еид
уравнения
называется
уравнением
в
отрезках.
Если
же
прямая задана
уравнением
у
»
fa +
b,
например
у
~
2х
+
1,
то ее
удобно
строить по-другому,
а
именно;
на
вертикаль-
ной
оси
найдем точку
В=
\(Ь=*\
ед.) (рис.
2,
б),
затем
«отойдем»
от
нее
на 1 ед.
вправо
по
горизонтали
и
после
этого
«поднимемся»
вверх
на
k
~
1 ед.
Через
полученную
точку
К и
через
точку
В и
проведем
искомую прямую
If,
Иногда надо построить
прямую,
проходящую через данную
точ-
ку
перпендикулярно данному вектору
—
нормальному вектору пря-
мой. Пусть точка
есть
(х
0
,
у,),
вектор
п
- (а,
и),
тогда уравнение
прямой
есть
а(х
-
*
0
)
+
Ь(у
-
y
Q
)
- 0.
Поэтому уравнение прямой
III
(рис.
2, б),
заданной
в
виде
1(х - 2)
+
3(у
- 1)
*=
О,
надо
строить
имеио
так: провести
ее
перпендикулярно
вектору
(2, 3)
через
точ-
ку
(2, I),
Приведем
еще
некоторые сведения справочного характера. Если
прямая
проходит через точку
(Х
0
,
^
0
),
то ее
уравнение имеет
вид
а(х
-
X
Q
)
+
Ь(у
-
;>„)
= 0 при
некоторых
а,
Ь.
Уравнение
прямой,
проходящей
через
точки
(х
0
,
у
0
)
и
{*,,
^,),
есть
(х
-
*„)/(*,
-
х
0
)
=
(у
<-
у
й
)/(у
{
-
у
0
).
Угол
ф
между
прямыми
с
угловыми
коэффициентами
£
р
^
2
на-
ходится
по
формуле
tg
tp
*
(#j
-
Л
2
)/(1
+
^,А
2
).
Необходимым
и
достаточным условием параллельности прямых
является
равенство
их
угловых коэффициентов:
k
:
=
&
2
(рис.
3).
Рис.
3
Необходимым
и
достаточным условием перпендикулярности
прямых
является равенство
fc,fc
2
=*
-1,
если
они
заданы уравнениями
30
вида
у -
he
+
b,
или
й,я
2
+
b
t
b
2
~
0,
если
они
заданы
уравнениями
вида
ах + by - с.
Точка
пересечения прямых
а
}
х
+
b
t
y
=
с,,
а
г
х
+
Ь^>~
с
2
опреде-
\a
l
x
+
b
l
y-c
l
,
ляется
как
решение системы уравнений
|
л
v4
,
A
,»-/.
I
И^А
™
***№
*"**
Со*
Горизонтальные
прямые имеют уравнение
у
=
Л,
вертикальные
прямые
имеют
уравнения
х =
d.
Биссектриса 1-го квадранта имеет
уравнение
у = х,
биссектриса 2-го квадранта имеет уравнение
у
+ х
=
0
(рис.
3).
2.
Линейные
функции
спроса
и
предложения, определение равно-
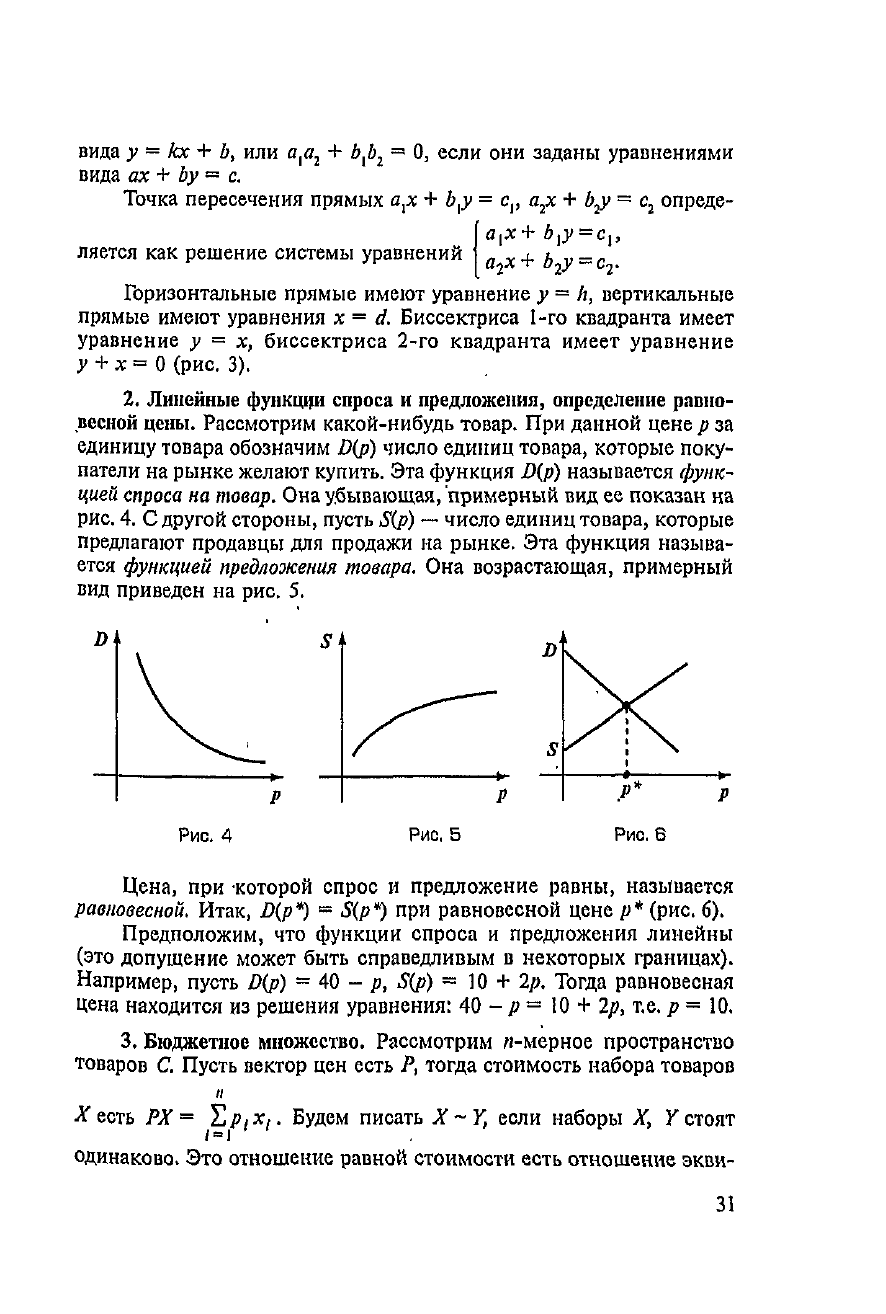
весной цены. Рассмотрим какой-нибудь товар.
При
данной цене
р за
единицу
товара обозначим
D(p)
число
единиц
товара, которые поку-
патели
на
рынке желают купить.
Эта
функция
D(p)
называется
функ-
цией спроса
на
товар.
Она
убывающая, примерный
вид ее
показан
на
рис.
4. С
другой стороны, пусть
S(p)
—
число единиц товара, которые
предлагают
продавцы
для
продажи
на
рынке.
Эта
функция называ-
ется функцией предложения
товара.
Она
возрастающая,
примерный
вид
приведен
на
рис.
5.
Цена,
при
-которой
спрос
и
предложение равны, называется
равновесной.
Итак,
D(p*)
~
5(р*)
при
равновесной цене
р*
(рис.
6).
Предположим,
что
функции спроса
и
предложения
линейны
(это допущение может быть справедливым
в
некоторых границах).
Например,
пусть
D(p)
- 40 - р,
$(р)
- 10 +
2/),
Тогда равновесная
цена
находится
из
решения уравнения:
40 - р -
Ш
+
2р,
т.е.
р
=
10.
3.
Бюджетное
множество. Рассмотрим
«-мерное
пространство
товаров
С.
Пусть вектор
цен
есть
P
t
тогда
стоимость набора товаров
я
Л'есть
РХ =
*Lp,x,.
Будем писать
X~Y
t
если наборы
X*
Y
стоят
/
=
i
'
одинаково.
Это
отношение
равной
стоимости
есть
отношение
экви-
31
