Малыхин В.И. Математика в экономике

Подождите немного. Документ загружается.

ной

их

числу (это,

конечном

счете,

есть атомный

взрыв),

Со-

ставьте

уравнение процесса размножения нейтронов.

За

полчаса тело охладилось

со 100 до

,50°С

(при

температуре

окружающей

среды

0°С).

Напишите уравнение процесса

охлаждения.

10.

Сопротивление воды прямо пропорционально скорости

лод-

ки.

Составьте уравнение движения лодки

пруду после

того,

как

гребцы

перестанут грести.

П.

Коэффициент выбытия фондов

равен

1/10,

инвестиции

по-

стоянны.

Опишите процесс движения фондов, рассуждая чисто

эко-

номически.

Подкрепите затем свое рассуждение

математическими

выкладками.

12.

Предположим,

что

месячный

доход

семьи

постоянный,

траты пропорциональны накоплениям. Стабилизируются

ли

накоп-

ления?

Тема

13.

ДИФФЕРЕНЦИАЛЬНЫЕ

УРАВНЕНИЯ

1-ГО

ВЫСШИХ

ПОРЯДКОВ

13.1,

МОДЕЛИ

ЭВАНСА

СОЛОУ

этом разделе изучим

две

широко известные

динамические

мо-

дели

экономического характера: сначала модель

Эванса

установления

равновесной

цены

на

рынке одного товара, затем

динамическую

од-

носекторную

модель экономического роста, известную

под

названи-

ем

«базовая модель

Солоу».

Модель Эванса. Рассматривается рынок одного товара,

время

считается непрерывным. Пусть

</(0»

-s(i),

ХО

—

соответственно

спрос,

предложение

цена

этого

товара

момент

t, И

спрос,

предло-

жение

считаются линейными функциями

цены,

т.е.

d(p)

- а

-Ьр,

b > 0 —

спрос

ростом цены падает,

s(p)

- а

р/>,

а ,

> 0

предложение

ростом цены растет. Естественно считать,

что

а>

т.е.

при

нулевой цене спрос превышает предложение (по-другому

го-

воря,

товар желателен).

Основное предположение состоит

том,

что

цена

изменяется^

зависимости

от

соотношений между спросом

предложением:

Др

192

y(rf

s)At,

где

> 0,

т.е.

увеличение цены прямо пропорционально

превышению

спроса

над

предложением

длительности этого пре-

вышения.

Итак,

получаем дифференциальное уравнение

dp/dt

7(rf

- s).

Подставляя

в это

уравнение линейные зависимости

спро-

са и

предложения

от

цены, получаем линейное неоднородное диф-

ференциальное

уравнение

начальным условием:

dp/dt

-т((й

®р

- а

а),

р(0)

=/v

(1)

Это

уравнение

имеет стационарную

точку/?'

- (я -

а)/(/>

+ р) > 0.

Видно,

что

dp/dt

> 0 при

р'

>р и

dp/dt

< 0 при

р'.

< р.

Отсюда следует,

что

\imp(f)

р\

При

р'

цена стремится

р'

возрастая,

а при

М°о

р*

—

убывая. Сама цена

р'

есть

равновесная цена

— при ней

равны

спрос

предложение:

d(p)

s(p)

-*a-bp-a,+

$p->

Р"

(а -

а)/(Ь

р).

Равновесная цена может быть найдена также

графически

— как

точка пересечения прямых спроса

d(p)

а -

Ьр

предложения

s(p)

а +

$р

(рис.

I).

п. 5

раздела

12.1

был

рассмотрен

метод

решения

уравнения

акого

вида

—

метод вариации постоянной. Согласно этому методу

щее

Рвение

есть сумма общего решения соответствующего одно-

Родного

уравнения

dp/dt

7(6

а)р

0 и

какого-нибудь частного

Решения

неоднородного уравнения

(1).

Не

останавливаясь

на

этом

ичас,

выпишем решение дифференциального уравнения

началь-

ным

условием

(1):

11ЛИ

ХО

Р^

Р)

+ (а -

се)/(й

Р)[1

г*

*®Ч

(2)

ХО

=де-К

№

Х[1

е-***»'].

Опять

же

видно,

что

lim

p(t)

р\

/-*

оо

193

Рассмотрим дискретный аналог модели

Званса.

дискретной

модели рынок функционирует следующим образом; утром

на

рынке

обнаруживается

некоторое предложение

s и

спрос

зависимости

от их

значений цена начинает равномерно расти

или

убывать:

если

утром

спрос

был

больше

предложения,

то

возрастать; если

предло-

•жение

было больше

спроса,

то

убывать. Предположим,

что

началь-

ная

цена была

при

этом

s(p

)

d(p

Следовательно,

цена

начнет

возрастать.

За

день

она

возрастет

до

некоторого значения

На

сле-

дующее утро предложение

спрос будут соответствовать этой

цене

при

этом опять будет

s(p^

d(p^

цена будет

возрастать

т.д.

(рис.

I).

Однако,

отличие

от

паутинообразной модели рынка (см.

п. 4

раздела

4.1), точка равновесия

не

переходится, т.е. если цена

была

меньше

равновесно^

то она так и

останется меньше,

весь

процесс

изображается

слева

от

точки равновесия,

если цена была

больше

равновесной,

то она так и

останется

больше,

весь процесс

изобра-

жается

справа

от

точки равновесия.

Параметры модели Солоу. Экономика

рассматривается

как

единое

целое (без структурных подразделений),

в ней

производится

единственный

универсальный продукт, который может

потребляться

как

непроизводственной сфере,

так и в

производственной;

потреб-

ление

его в

производственной сфере может рассматриваться

как

инвестирование

(с

некоторой натяжкой таким «продуктом»

может

выступать

денежная оценка всего

вся).

Эта

модель достаточно

адек-

ватно

отражает важнейшие макроэкономические аспекты,

в том

чис-

ле

процесса воспроизводства.

Состояние экономики

модели

Солоу задается пятью

перемен-

ными

состояния:

Y —

конечный продукт,

L —

наличные

трудовые

ресурсы,

К —

производственные

фонды,

—

инвестиции,

С -

раз-

мер

непроизводственного потребления.

Все

переменные

взаимосвя-

занно

изменяются

во

времени,

т.е.

являются функциями

времени

но

далее аргумент

будет часто опускаться, хотя

будет

подразуме-

ваться

по

умолчанию.

Время

будет предполагаться непрерывным.

Для

мгновенных

показателей

К,

можно считать,

что

L —

соответственно

фонды

трудовые ресурсы

момент

или,

чтобы

избежать

сезонных

изме-

нений

числа занятых

всплеска фондов

при

вводе новых

мощнос-

тей,

Км

можно считать средними значениями этих величин

за

год,

серединой

которого

служит

/. Для

величии

же У, С,

их

значения

момент

можно себе представить,

как их

объемы,

накопленные

год,

серединой

которого служит момент

(но и в

этом случае

остаются

функциями времени

и их все же

лучше

воспринимать

194

мощность

производства

мгновенные скорости потребления

и ин-

вестирования).

Считается,

что

ресурсы (производственные

трудовые) исполь-

зуются

полностью. Годовой конечный продукт

каждый

момент

времени

является функцией среднегодовых фондов

труда:

Y -

~f[K

}

V).

Таким образом,

F(K,

L) —

производственная функция все-

го

народного

хозяйства.

Конечный

продукт используется

на

непроизводственное потреб-

ление

инвестиции:

С +

Назовем

нормой накопления

долю

конечного продукта,

используемого

на

инвестиции,

тогда

/—

рУ,

С - (1

р)К

даль-

нейшем

норма накопления будет считаться постоянной:

р —

const,

0<р<

Инвестиции используются

на

восстановление

выбывших фон-

дов

и на их

прирост

(считается,

что эти

инвестиции расходуются

только

на эти

цели

— для

сравнения

см.

задачу

«Б» п. 2

раздела

12.1)).

Если

принять,

что

выбытие происходит

постоянным коэффициен-

том

выбытия

\i,

О <

< 1 (в

расчете

на

год),

то

К**

АО

рШ

цйМ,

поэтому

dtf/d/

Y-

\аК.

Если

считать,

что

прирост

трудовьшресурсов

пропорционален

наличным

трудовым

ресурсам,

т.е.

Д£

•

Д/,

то

получаем диффе-

ренциальное

уравнение

dL/dt

и,

решая

его,

получаем

Z-

где

до)

—

трудовые ресурсы

начале наблюдения,

при t

Таким

образом,

модель Солоу

задается

схемой

(рис.

2) или

системой

Уравнений:

С=(1-р)У;-

Wi);

(3)

*«V

d^/dr=

r-^,

АГ(0)

ЛГ

Функция

F(K

удовлетворяет

требованиям

производственным

Функциям

(см.

п. 3

раздела

6.1

или п. 1

раздела

9.2)

считается

ли-

нейно-однородной,

т.е.

f{KK

XI)

ХДАГ,

L).

Пользуясь

ее

однород-

ностью

обозначив среднюю производительность труда

у -

К/1

^среднюю

фондовооруженность

K/L,

получаем

у -

Y/1

•••

ЦК,

L)/L

ДЛ/1,1)

F(k

1), а

если обозначим последнюю

функ-

ЦИ1

оДА),

то

получаем

=/(*).

найдем производную

от k по

d/c/d/

d(K/L)/dt«(JC'i

Л1

)да

j^yx

д/

у„

цл)

v/L

„

(|1

)ft.

Окончательно:

dft/dr«

рДЛ)

- (ц +

v)/:,

ft(0)

Ayi

(4)

19S

Поведение макропоказателей модели

(3)

целиком

определяется

уравнением

(4) и

динамикой трудовых ресурсов

Уравнение

(4) — это

уравнение

разделяющимися

переменны-

ми

начальным условием, поэтому

оно

имеет единственное

реше-

ние.

Исследуем только некоторые специальные решения этого

урав-

нения.

Стационарные траектории

модели Солоу. Рассмотрим

стаци-

онарную

траекторию,

т.е.

такую,

на

которой

фондовооруженность

постоянна

равна,

следовательно,

своему начальному

значению;

k(t)

const

Но

поскольку таким постоянным значением

может

быть,

наверное,

не

всякое начальное, обозначим

его

А°.

Такое

значение фондовооруженности называется

стационар-

ным.

Конечно,

на

стационарной траектории

dfc/df

Рассмотрим,

как на

стационарной траектории ведут себя мак-

ропоказатели

К,

С,

Согласно уравнению

(4),

если dk/dt

= 0, то

р/Ш

(М-

v)A

т.е.

А°

есть решение уравнения

Р/Ш

- (Ц +

v)/c

0. (5)

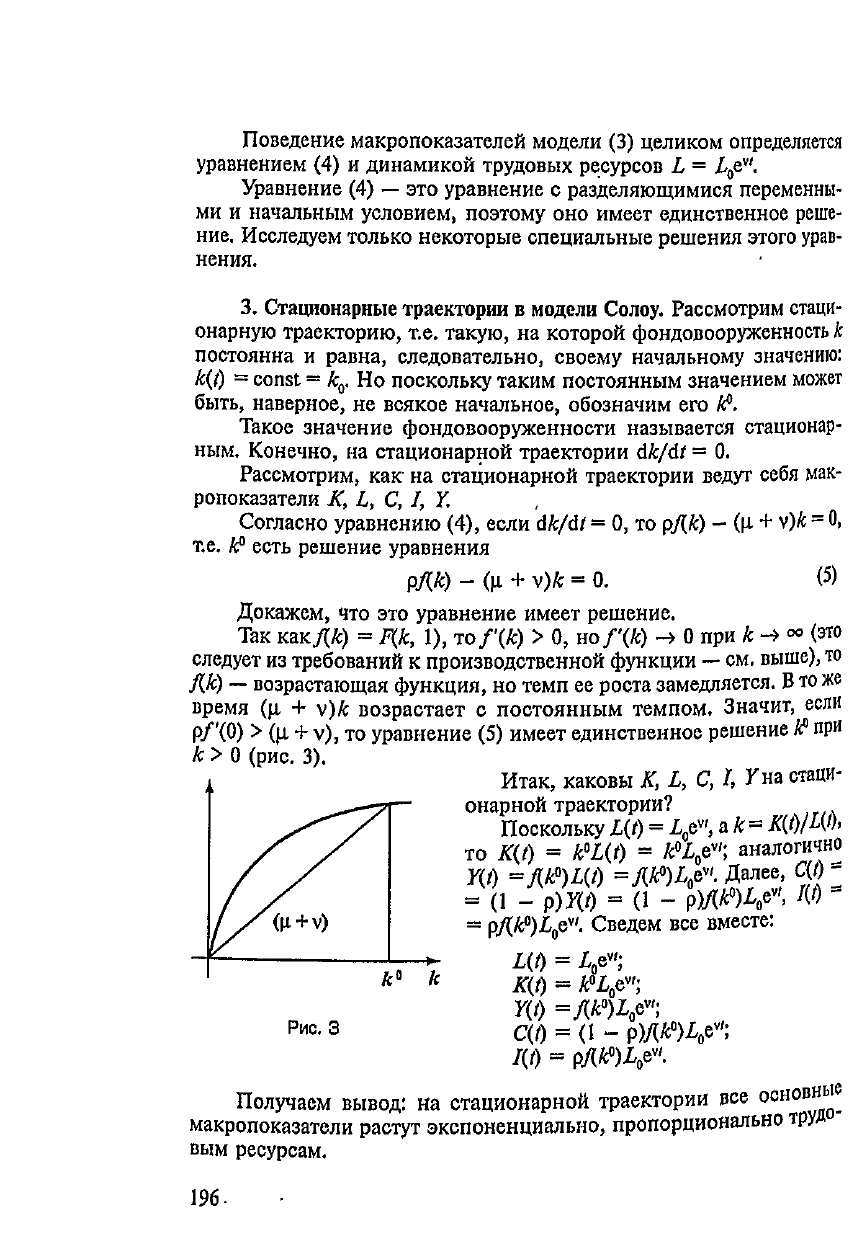
Докажем,

что это

уравнение имеет решение.

Так

какДЛ)

ДА,

1),

то/'(£)

> 0,

но

/'(Л)

-»

0 при k

(это

следует

из

требований

производственной функции

— см.

выше),

то

ДА)

—

возрастающая функция,

но

темп

ее

роста замедляется.

В то же

время

(р,

v)£

возрастает

постоянным темпом. Значит,

если

р/'(0)

(р,

v), то

уравнение

(5)

имеет единственное решение

А°

при

k > 0

(рис.

3).

Итак, каковы

К,

С,

/на

стаци-

онарной траектории?

Поскольку

ДО =

K(t)/W

то

ДО

А°ДО

*°А>еЧ

аналогично

ДО

=лW)

=ЛА°)V-

Д^;

р)ДО

PWWV-

/(/)

рДА°)^

Сведем

все

вместе:

до =

;

до

;

У(0

=ЛА°)1

С(0

= (1 -

Р)Д«Ае«;

ДО

p/WV

Получаем вывод:

на

стационарной траектории

все

основ

макропоказатели

растут экспоненциально, пропорционально

труд

вым

ресурсам,

196.

Конкретизируем

описанный общий случай применительно

производственной

функции

Кобба-Дугласа

F(K>

Л>0,0<,а<

Поскольку

при

этом

=F(k,

^AP,

то

уравнение

(4)

принимает

вид: dk/dt

рА№

(|i

v)fc,

fc(0)

Это

уравнение

разделяющимися переменными

и его

можно

было

решить

по

общему правилу (см.

п. 4

раздела

12.1),

но

оказалось

удобнее

решить следующим образом.

Сделаем замену переменной

k(t)

и(/)е-^

где

и(/)

новая

функция

от

Тогда получим:

dk/dt

du/dt

•

е-**

»'-

(ц.

v)e-<>

l+v

j'H(/),

и,

подставляя

вместо

k его

выражение через

и,

получим:

рДне~

(11+у)г

)

(ц

у)(ие-<"

du/dt

•

(ц.

v)e-

(

v)1

и.

Преобразуя

далее,

получим уравнение относительно

и:

du/dt

рЛн^е

а)(

«(0)

которое

легко

решается:

dw/M

рЛ

a)(|t

1/(1

ay-

рЛ/((1

<х)(ц

у))е"

v)/

с,

отсюда

(Аг

рД/(|1

v))/(l

а),

рЛ/(ц

+ v)

[е*

-«>»

»>'

- 1] + V

Окончательно,

н(/)

(*„'

Л/(ц

v)[e«

a)(l

1])

1/(I

Следовательно,

k(t)

u(f)

(

v)/

Видно,

что

Urn

k(t)

[рЛДц

v)]W'-«o.

?->

Но

нашем случае уравнение

(5),

т.е.

р/Ш

(Ц

v)A

имеет

вид

р/1Л°

(ц +

v)/:,

стационарное значение фондовооруженности

Для

функции

Кобба-Дугласа

равно

А°

[р^/(ц

v)]

1/(t

Следовательно,

при

любом начальном значении

фондовоору-

женность

k(f)

сходится

стационарному значению

А°.

Поскольку

ХО

Л№,

то и

производительность труда сходится

стационарному

значению

= Л •

[рЛ/(ц

v)]^'-

Поэтому

удельное потребление

(на

одного

работающего)

также

сходится

стационарному значению:

lim

С(/)/ДО

/_>00

Нт

р)ХО

(1 -

р)Л[рЛ/(И

v)]^'-

При

исследовании

модели

вполне разумно принять

качестве

критерия

успешности развития экономики величину удельного

по-

требления.

Найдем,

при

каком значении нормы накопления

предельное

удельное

потребление,

равное,

как мы

увидели, удельно-

потреблению

стационарном режиме, максимально.

Для

этого

продифференцируем

эту

величину удельного потребления:

РЫ[рД/(ц

)]

по р и

приравняем производную нулю:

((1

РМ[рЛ/(р,

v)]

>)'

О,

((1

p)p

a/cl

)'=

После несложных

чыкладок

получим

р'

а.

«Золотое правило» экономического роста. Итак, оптимальная

"орма

накопления

стационарном режиме равна коэффициенту эла-

197

стичности

по

фондам

(«золотое

правило» экономического

роста).

Но

это

справедливо

для

производственной функции

Кобба-Дугласа.

Для

других

производственных

функций

это

правило,

вполне

возможно,

будет другим,

ЗАДАЧИ

Решите подробно уравнение

(1).

Выпишите

явном

виде

функции спроса

предложения

уже

как

функции

времени, воспользовавшись найденной

зависимостью

цены

от

времени

(см.

формулу

(2)).

13.2. НЕКОТОРЫЕ ОБЩИЕ СВЕДЕНИЯ

ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЯХ

•

1.,

Метод

Эйлера приближенного решения

дифференциальных

уравнений.

Класс дифференциальных

уравнений,

интегрирующихся

.квадратурах,

т.е.

решения которых можно записать

виде

интегра-

лов,

Крайне

узок,

и,

поэтому нужды теории

практики

потребовали

'развитии

методов нахождения

Приближенных

решений

дифферен-

циальных

уравнений. Справедливости ради нужно сказать,

что

не-

специалисту

по

дифференциальным уравнениям

или

численным

методам вряд

ли

имеет смысл самому заниматься поиском

прибли-

женного

решения.

Однако

некоторые

основополагающие

моменты

этих

методов

знать полезно.

Отметим'также,

что

нахождение приближенного

решения

вруч-

ную

весьма

трудоемко,

точность приближения получается

недоста-

тбчной,

использование

компьютера представляется

неизбежным.

•

Отметим также,

что

теперь,

развитием вычислительной

техни-

ки,

часто целесообразно применять приближенные методы

даже

tcx

случаях,

когда уравнение интегрируется

квадратурах. Более

того,

это

целесообразно даже

в тех

редких случаях, когда

решение

выра-

жается

элементарных функциях,

так как

использование

таблиц

значений

этих функций (показательной, логарифмической,

триго-

||ом"стри'ческих)

оказывается более

трудоемким,

чем

приближенное

'интегрирование

уравнения

на

быстродействующем компьютере.

Рассмотрим

метод

Эйлера приближенного решения

дифферен-

циальных

уравнений.

Это —

один

из

самых старых

простых

мето-

дов^

приближенного решения дифференциального уравнения

d>»/d*

~Лх,

и;

Суть

метода

том,

что

искомая интегральная

кривая

этого

урав"

.нейия,

Проходящая

через

точку

(х

заменяется ломаной

линией,

состоящей

из

прямолинейных отрезков

каждое звено

которой

ка-

сается интегральной кривой

одной

из

своих точек (рис,

1).

198

При

применении

этого

метода

для

приближенного вычисления

интегральной

кривой

на

отрезке

[я,

Ь],

а <

Ь,

этот

отрезок

разбива-

ется

на

равных частей точками

< ... <

и Л -

(Ь

а)/п

называется

шагом вычисления. Будем обозначать приближенные зна-

чения

искомого решения

точке

х,

через

у,,

значение

Дх

у) че-

рез

у;.

Для

вычисления

заменим

на

отрезке

[х

]

искомую интег-

ральную

кривую отрезком

ее

касательной

точке

Следовательно^

У\

^'<Л

аналогично,

j>,

у\Н

т.д.

Окончательно:

^-1

.,А.

Получается

так

называемая

ломаная

Эйлера, Естественно ожи-

дать,

что при А

-»0

ломаные Эйлера приближаются

графику иско-

мой

интегральной кривой

и,

следовательно,

уменьшением

шага

метод

Эйлера

дает

все

более

точное значение решения

на

отрезке

[я,

Ь].

Это

действительно

так,

если

функция

Дх,

у)

удовлетворяет

не-

которым,

не

очень ограничительным

практической точки зрения

УОЛОВИЯМ

(см. далее

п. 2),

Из-за своей простоты метод Эйлера

до-

вольно

часто

применяется

на

практике

—

ведь самым сложным

Нем

является вычисление

значений.}';

-Д*,,

у)*

Однако

при

система-

тической

нужде

нахождении приближенных решений приходится

применять

более точные

методы,

которых можно прочитать

спе-

циальной

литературе.

Теорема

существования

единственности

решения.

Если

урав-

нении

dy/dx

=Дх,

у)

функцияДя,

у)

непрерывна

прямоугольнике

- а

+ a,

удовлетворяет

прямо-

Угольнике

условию Липшица:

|Дх,

j»,)

Дх,

j»

N •

Ь,

—

константа,

то в

некоторой

окрестности

точки

существует един-

ственное

решение

уравнения,

проходящее через

эту

точку.

Теорема

гарантирует существование

единственность решения

ишь

некоторой окрестности точки

Однако

если

граничной

точке

этой окрестности условия теоремы опять выполнены,

то это

Решение

может быть продолжено

еще на

некоторую окрестность

уже

этой

граничной

точки;

целом получится

еще

больший

отрезок,

чем

первоначальный,

т.д.

199

Что

касается условия Липшица,

то оно

удовлетворяется,

если,

например,

функция

Дх,

у)

имеет

прямоугольнике

ограниченную

частную

производную

по у.

Доказательство этой теоремы основано

сущности

на

том,

что

условиях теоремы ломаные Эйлера

пределе

дадут

интегральную

кривую.

силу практической важности теория дифференциальных

урав-

нений

развита весьма хорошо.

Вот

пример теоремы

свойствах

ре-

шений

дифференциального уравнения.

Теорема

дифференцируемости

решений.

Если

некоторой окрестности точки

т.е.

некотором

прямоуголь-

нике

вокруг

этой

точки,

функцияу(х,

у)

имеет непрерывные

частные

производные

до

л-го

порядка включительно,

то

решение

у(х)

уравне-

ния

dy/dx

=/(х,

у),

удовлетворяющее

условию

Х*

)

~Уо

(

это

решение

существует

по

только

что

рассмотренной

теореме),

некоторой

ок-

рестности

точки

имеет непрерывные производные

до

п-го

порядка

включительно.

Понятие

об

устойчивости

решений

дифференциального

уравне-

ния.

Для

возможности математического описания

какого-нибудь

реального

явления неизбежно приходится упрощать его,

выделяя

учитывая

лишь наиболее существенные

из

влияющих

на

него

факто-

ров и

отбрасывая остальные, менее существенные.

При

этом

неиз-

бежно

встает вопрос

том, удачно

ли

выбраны упрощающие

пред-

положения.

Возможно,

что

неучтенные факторы сильно

влияют

на

изучаемое-явление,

значительно меняя

его

количественные

или

даже

качественные

характеристики.

Рассмотрим дифференциальное уравнение

dy/dx

=/[*>

У)

на

чальным

условием

у(х

)

Подобные начальные условия

обычно

являются

результатами измерений

и,

следовательно,

получены

с не-

которой

погрешностью. Возникает вопрос

влиянии этих

погреш-

ностей

на

искомое

решение.

Если

окажется,

что

сколь

угодно малые изменения

начальных

данных

способны сильно изменить

решение,

то

такое решение

обыч-

но не

имеет никакого прикладного значения

и его

нельзя

применить

Для

описания изучаемого явления. Если

же

малые

изменения

на-

чальных

данных лишь незначительно меняют само"

решение,

то го-

ворят,

что

имеет место непрерывная зависимость решений

от

началь-

ных

данных. Вопрос

непрерывной зависимости является

практиче-

ски

важным.

Теорема

непрерывной

зависимости решения.

При

выполнении условий теоремы существования

единственности

решения

(см. выше) решение уравнения непрерывно зависит

от на-

чальных

данных

некоторой окрестности точки

200

Поясним

эту

теорему.

Для

этого

обозначим через у(х,

.у

)

единственное

решение уравнения

dy/dx

-J(x,

у),

которое

при х

=х„

принимает

значение

;

соответственно

у(х

}

х ,

у)

обозначает реше-

ние,

которое

при х

принимает значение

((х

}

у)

—

точка,

близ-

ки

)).

Из

теоремы существования

единственности решения (см.

п. 2)

можно

вывести,

что

найдется такая окрестность

точки

т.е.

некоторый

прямоугольник

содержащий точку

)

внутри

себя,

такая

окрестность

точки

(т.е. отрезок

содержащий точку

х„

внутри

себя),

что-для

любой точки

(х , у ) € К

существует единст-

венное

решение

у(х,

х ,

у),

проходящее через

эту

точку

опреде-

ленное

на

окрестности

Так

вот,

теорема

непре-

рывной

зависимости решения

от

начальных

данных утвержда-

ет,

что для

любого

е > 0

найдет-

ся

такой

прямоугольник

К,

что

как

только

(х

у)

е Р, то

Ь(Х>ХЬ,У

)-У(Х

}

7)|

<£

на

всем

отрезке

/(рис.

2). То

есть

если

точка

(х

, у )

будет близка

кточке

(д:

то

соответствующие интегральные кривые тоже будут

олизки

друг

другу

на

всем интервале

Эта

теорема

непрерывной зависимости решений

от

началь-

вал

УСЛОВИЙ

устанавливаеттак

зависим

ость

на

некотором интер-

готс

Кон

ечной

Д^ины

вокруг начальной точки

Если

же

исследу-

Уст

ДобНЫе

вопросы

на

бесконечном

промежутке,

то

говорят

об

ки

оости

решения.

Понятие устойчивости является

практичес-

важным,

неустойчивые решения

редких случаях представляют

интерес

на

практике.

Понятие

дифференциальных уравнениях высших порядков

MiiX

Дифференциальных

уравнений. Дифференциальные уравне-

го

порядка имеют

вид

F(x,

у,

.,.,

У«>)

или, если

они

шены

относительно старшей производной:

/">

=У(х,

Л/>

...,У"-'>).

(1)

Для

таких уравнений также имеет

место

следующая теорема.

Ния

у°

рема

УЩ

ес

твования

единственности

реше-

•

Уравнение

(1)

имеет единственное решение

у(х),

удовлетворя-

201