Малыхин В.И. Математика в экономике

Подождите немного. Документ загружается.

132

ческой

теории, зародившегося

середине

XIX в.

Одним

из

осново-

положников

этого течения

был

немец

К.

Госсен,

Он

первый

сформу-

лировал

основополагающее свойство функции полезности:

увели-

чением

потребления

товара

его

полезность

уменьшается

— это и

есть

так

называемый

1-й

закон Госсена.

То

есть если

вы

голодны,

то

пер-

вый

гамбургер съедите

большой

охотой,

второй

уже не так

понра-

вится

т.д.

На

дифференциальном языке

это

означает,

что

предель-

ные

полезности убывают

при

возрастании аргументов

—

количеств

•потребляемых

товаров, т.е. вторые частные производные

должны

быть отрицательны.

Пример

3. Для

функции

полезнос-

ти

и(х,,

)

у*1

у*2

начертить кривые

без-

различия

(линии постоянства

полезности).

Найти

вектор

предельных

полезностей,

про-

верить

выполнение

1-го

закона Госсеиа.

Решение,

Построим

кривые

постоянст-

ва

полезности

—

{(*,,

у*|

(рис.

2).

Найдем

частные

производные:

Эй/Эх,

1/*Г/(2

/*Г),

Эй/Эх,

/*Г/(21/*Г)-

Следовательно, вектор предельных

полезно-

стей

есть

(^7/(2

/*7),

/*T/(2

fii))•

Для

проверки

1-го

закона Госсена находим вторые частные

производ-

ные:

и"

-(i/4)v-va

1/2

ц-

-(I/to"

х-"

они

отрицательны,

что

2^2

свидетельствует

выполнении

1-го

закона Госсена,

функциям полезности относятся, например:

функция

стоимости

«(#,,

)

с,*,

;

неоклассическая

функция

ы(х

)

х^х

где

а,,

°'

а,

< 1.

Еще

одна функция

—

иЦ,

)

min

{/ее,,

тх

где

Аг,

является

несколько особой

представляет интерес

как

крайний

случай.

ЗАДАЧИ

Опишите,

из

чего складывается увеличение объема

прямого

кругового

цилиндра

при

небольших увеличениях радиуса

его

осно-

вания

и его

высоты. Проведите аналогичные исследования

по

пово-

ду

объема прямоугольного

параллелепипеда

при

небольших

увели-

чениях

трех

его

измерений,

также

площади

треугольника

как

функции

трех

его

сторон (см. пример

1 из п.

раздела 7.1).

Найдите дифференциалы функций

общем виде

и в

точке

(1,1):

а)

(х

+^)

;б)и=х

4х

в)

и=ху+х-у.

. 3.

Найдите предельные полезности

градиент

различных

точ-

ках

функций

полезности:

а) и

Зя,

5х

;

б) и

min

{*,,

2х

4. На

карте местности обычно проводят горизонтали

—

линии

постоянной

высоты. Можно

ли по

этой карте узнать примерные гра-

диенты

разных точках?

Тема

ЗАДАЧИ

ОПТИМИЗАЦИИ

ЭКОНОМИКЕ

9.1.

ЭКСТРЕМУМЫ

ФУНКЦИЙ

МНОГИХ

ПЕРЕМЕННЫХ

Экстремум

функции

его

нахождение.

По

ходу

изложения

будем

напоминать

соответствующие

понятия

для

функции

одной

переменной,

„

Определение

экстремумов функции одной переменной

было

Дано

разделе

5.2.

силу

важности

этого понятия напомним

его еще

раз.

Значение

функции

называется

максимумом (минимумом)

ФУНКЦИИ

Дя),

если

оно

является наибольшим (наименьшим)

неко-

торой

окрестности

точки

е>

т.е.

этой

окрестности

вьшолняется

не-

равенство

Ях)

</(я)

№)

>№)).

Соответствующее

значение аргумен-

та

называется

точкой

максимума

(минимума).

Максимумы

ми-

нимумы

функции называются экстремумами

функции,

точки

мак-

симума

минимума

точками

экстремумов.

ffUUMY

тпчио

Определение

экстремумов

функции многих

пере^

енных

точно

такое

же.

Напомним только,

что в

одномерном

слу^*P«*™^

точки

есть

любое

множество,

содержащее открытый

«"^"

°^Г

РОМ

этой точке.

многомерном

же

случае

под

°^?™^

™^

понимается

любое

множество,

содержащее

<^ы«и

шар

GW^M

этой

точке

(см.

п. 3

раздела

7.2).

То

есть

**№™№Ъ^™_

обычное

расстояние

между числами заменяется

Р"^""^."^.

лидовом

пространстве,

котором

определена

функция многих пере

Меиных

Напомним,

что

точка является

внутренней

^кой^н.^и

некоторая

окрестность

точки целиком содержится

этой области.

133

Точка

называется критической точкой функции

f(x),

если

f'(a)

— 0 или

/'(о)

не

существует. Точка

называется

стационарной

точкой

функции

./(я),

если

она

есть внутренняя точка области

опре-

деления

функции

/'(а)

— 0.

Теорема

(необходимый

признак

эстремума).

Если функция

имеет

во

внутренней

точке

экстремум,

то эта

точка

являет-

ся

критической

точкой

этой

функции

стационарной,

если

в пей

существует

производная.

Пусть теперь

=Дх

...,

*$)

—

функция

переменных.

Точно

так же, как

случае одной переменной, точка

называ-

ется критической точкой

функции,

если

все

частные

производные

равны

нулю

или

какая-нибудь

из них не

существует. Точка

называет-

ся

стационарной

точкой

функции,

если

она

есть внутренняя

точка

области

определения

и все

частные производные равны нулю.

Теорема

(необходимый

признак

эстремума функции многих

пере-

менных).

Если функция имеет

во

внутренней

точке

экс-

тремум,

то эта

точка

является критической точкой

этой

функции

и-стационарной,

если

в ней

существуют

все

частные производные.

Доказательство точно такое

же, как и для

функции одной

пере-

менной

(см.

п. 1

раздела 6.1).

Итак,

«подозрительными»

на

экстремум

являются

те

точки,

которых

все

частные

производные

равны нулю

или

какая-нибудь

из

них

не

существует;

случае если функция

всюду

имеет

частные про-

изводные,

то

координаты этих

точек

можно найти, решив

систему

уравнений:

Эм/cbc,

-О,

Эи/Эх

Пример

Найти

ркстремум

функции

(у -

Найдя

частные

производные

приравняв

их

нулю,

получаем

систему

уравнений:

|Эг/Эх=2х

= 0,

[Эг/^

2(у-1)

Решение

этой

системы

очевидно:

х - 0, у

Поскольку

при

всех

х,

у,

то

ясно,

что

найденная

точка

(О, 1)

есть

точка

минимума.

Достаточное

условие экстремума.

Конечно,

рассмотренный

пример

очень простой.

Для

функции одной переменной есть про-

стые достаточные признаки экстремума (см.

п. 1

раздела

6.1).

134

Теорема

(первый

достаточный

признак

экстремума).

Нусть^х)

непрерывна

некоторой

окрестности

точки

а а

диффе-

ренцируема

в ней

всюду,

кроме,

быть

может,

точки

а.

Тогда:

еслиГ(х)

>0нрих<а

uf'(x)

< 0

при

х>а,

то а

есть

точка

максимума

функции;

если

(к)

<0прих<а

uf'(x)>

0прих>а,тоа

есть

точка

минимума

функции.

Теопема

(второй достаточный признак

экстремума).

Пусть

f(x)

ее

производные

f'(x)

непрерывны

некоторой

окрестности

точки

а и

пусть/'(а)

- 0.

Тогда-.

если

Па)

< 0, то а

есть

точка максимума функции;

еслиГ(а)

то а

есть

точка минимума

функции.

Для

функций многих переменных достаточные

признаки

экс-

тремума

много

более

сложные.

Ограничимся

функциями

двух

пере-

менных.

„

ДЛ

Пусть

Ах,

у) и

стационарная

точка,

т.е.

-ЛСЛО?

Обозначим

=/"

/"„(*»>

D -

АС

- В.

Ъощьг

(достаточный

признак

экстремума).

й**В>ОиА^

<0,

то

точке

максимум,

если

J)>OuA>0,mo

ми

тшум.

Если

же D <

то

экстремума нет.

Что

касается

нахождения наибольшего

™™™"™^

ний

функции

на

каком-нибудь

множестве,

то

действовать надо

точ

но

так

же,

как и в

случае одной переменной.

значениями,

-ss3s=r=:r=,==

K5=rssss-J2Hs=n=

ФУНКЦИИ

достигается,

то

он

достигается

«^±Гособая

точ-

Допустимого

множества.

Угловая

точка

™

"®

ства

ка,

обязательно лежащая

на

границе

исследуемого

множества.

135

Условней

экстремум, метод множителей

Лагранжа.

Пусть

надо

найти

экстремум функции

ДЛ)

=f(x

•••>

х,)

при

наличии

нескольких

ограничений

вида

;

(Л)

-0,у=

I,...,

т;

т<п.

Поступают

следующим

образом:

а)

составляют

функцию

Лагранжа

L(X)

=J(X)

Х/р,(А)

уже

от

/«]

' '

+ т

переменных

(п

прежних

лс,...,

и /и

новых

...,

);

б)

составляют

решают систему уравнений:

az/axj^o,

эл/эх„=о,

эг/эх^о,

Wx,,,==o,

т.е. находят «подозрительные» точки

на

экстремум

функции

Лагранжа;

в)

решается вопрос

наличии

«подозрительной» точке экс-

тремума

(например,

помощью теоремы

2 — см.

выше),

при

этом

предполагаются

выполненными

соотношения;

1Э<р//Эл;

сЦ=0,/=

...,

т.

Задача оптимизации выбора потребителя.

Эту

задачу рассмот-

рим

качестве приложения описанного метода нахождения

услоР-

ного

экстремума

помощью множителей Лагранжа.

Будем

считать,

что

каждый товар имеет

цену/>,,

индивид

имеет

доход

—

какое-то количество денег,

рамках которого

он и

дейст-

вует,

покупая

нужный

ему

набор товаров.

На

покупку набора

товаров

Х~

(*,,

...,

х)

надо затратить

денег

количестве

с(Х)

+ ...

•п

П^

Х*

Таким

образом,

индивид

может

купить

только

/=м

такой

набор

при

котором

РХ

Следовательно,

множество

наборов

товаров, доступных

ему при

доходе

есть

В -

В(Р>

(X:

О, РХ

Q],

Это

множество называется бюджетным

(см-

также

п. 3

раздела

2.1).

е н и е

Бюджетное множество ограничено

замк-

нуто.

Доказательство, Пусть

/>,,

тогда,

как

легко видеть,

если

*е

В,

то

х,

Q/гдля

- 1,

...,

л,

т.е.

множество

ограничено.

136

Докажем

замкнутость. Пусть

В для

всякого

N и

-»

Тогда

силу

непрерывности линейной

функции

/£

и,

поскольку

Л^

то и

/>Z

Следовательно,

£.

Границей

бюджетного

множества называется множество

G —

{Хе

В: РХ

Q}.

Граница

G — это

отрезок

случае двух товаров,

часть

плоскости,

ограниченная треугольником,

случае трех

това-

ров,

и в

общем случае есть

часть

гиперплоскости

пространстве

товаров.

Бюджетное множество

В(Р,

зависит

от

дохода

системы

Цен

Р, но от

каких-либо характеристик

индивида,

например системы

его

предпочтений,

не

зависит.

Потребитель,

имея'доход,

желает

его

потратить

и,

естественно,

максимальной

пользой.

Польза понимается

смысле системы

его

предпочтений

или его

функции полезности.

Это

приводит

следую-

щей

задаче математического

программирования.

Найти

набор товаров

Х~

(*,,

....

х),

максимизирующий функ-

цию

полезности

u(x

..,,

х,)

при

выполнении бюджетного ограниче-

ния

px=*px

+...

+рх

б; по

смыслу задачи

все

переменные при-

нимают

неотрицательные значения,

т.е.

х,

- 1,

...,

п.

Рассматриваемую задачу можно сформулировать более кратко:

и(Х)

-~>

max,

PX<Q,

X>Q

или

даже

так;

{и(Л)-»тах,

(1)

\X^B(P

Q).

Поскольку

и(Х)

—

непрерывная функция своих аргументов,

бюджетное

множество

ограничено

компактно,

то

и(А)

достигает

на

множестве

своего максимума,

т.е.

решение задачи

(1)

существу-

ет.

Очевидно,

что

любая точка

максимума функции

с(Д)

лежит

на

границе

бюджетного

множества.

Действительно, если предполо-

жим

противное,

т.е.

что Z —

точка максимума,

но Z

(7,

тогда

< Q,

Однако

тогда

потребитель имеет неиспользованное количе-

ство

денег

Q -

и на

эти

деньги

он

может купить какой-то

допол-

нительный

набор товаров

Г,

причем можно

считать,

что

Г>

0. Но

тогда

У<=

в,

однако

u(Z

«(Z)

силу

того,

что

каждый товар

«едателен.

Получили противоречие

тем,

что Z -

точка максимума

ФУНКЦИИ

с(А)

на

бюджетном множестве.

Предложение

Если

и(Л)

строго вогнута,

то

решение

зада-

(О

единственно,

т.е.

существует только одна точка максимума

ФУНКЦИИ

полезности

на

бюджетном множестве.

137

Напомним,

что

функция

и(Л)

называется строго вогнутой,

если

для

любых

из

того,

что 0 < X < 1

следует,

что

и(Ъ;

+ (1 -

X)Y)

>г«(Л)

-\}u(Y).

Доказательство.

Предположим,

что Л и

С—две

точки

максиму-

ма,

т.е.

и(Х)

и(А)

—

и(С)

для

любой точки

ЛГ

множества

В. Мы

уже

знаем,

что

точки

А и С

лежат

на

границе

бюджетного

множества,

т.е.

РА - РС =

Рассмотрим точку

Б~А/2

С/2.

Видим,

что

РЕ~

Р(А/2

С/2)

т.е.

Я.

силу строгой вогнутости

функции

и(Л)

имеем:

н(£)

и(Л)

—

и(С).

Получили противоречие

тем,

что А

есть точки максимума функции

на

бюджетном

множестве.

Итак,

при

строгой вогнутости функции полезности

существует

бюджетном множестве

единственная

точка максимума

функции

по-

лезности.

Таким

образом,

потребителя

даже

нет

выбора

том,

как

наибольшей пользой потратить свои

деньги,

так как

сущестаует

единственный

набор

товаров,-максимизирующий

полезность.

Эта

единственная

точка максимума называется точкой спроса

или

про-

сто

спросом потребителя. Будем обозначать

эту

точку

X'.

Изучим

точку спроса. Пока установлено только,

что она

должна

лежать

на

границе бюджетного множества. Таким образом,

задача

(1)

сводится

следующей:

u(X)

max,

\PX~Q

или

(й(Л)->тах,

/2)

\X*B(P

Q).

Эту

задачу можно решить

помощью множителей

Лагранжа

Составим

функцию

Лагранжа

L(X

X) =

u(X)

X(Q

/»A),

найдем

частные

производные

приравняем

их к

нулю:

П/ЪХ~

0, f

dufiX-

ХР=

0, f

Ъи/ЪХ=

КР,

1Э//ЭХ-0,

\Q-PX~Q,

1<2-№=0.

Характеристика

точки спроса. Получаем следующий

вывод,

точка

спроса лежит

на

границе бюджетного множества

характери-

зуется

тем,

что в ней

вектор предельных полезностей

пропорциона-

лен

вектору

цен.

Можно

и так

сказать:

точке спроса

отношени

предельной

полезности товара

к его

цене есть величина

постоянная.

(Ъы/дх)/р

(

V для

любого

,..,

п,

т.е.

если, скажем,

/-и

товар

в 3

раза

дороже

у'-го

товара,

то

уменьше-

ние

его на

единицу компенсируется

(с

точки зрения функции

плезн

сто) увеличением

у-го

товара

на три

единицы.

Это

можно

вырази

так: взаимозаменяемы такие количества товаров, которые стоят

од

138

каково.

Иными

словами,

индивидууму невыгодно потреблять

одно

благо

вместо

другого,

стоящего

столько

же, и

вообще

как-то

изме-

нять

структуру

потребления,

поскольку всякое такое изменение

мо-

жет

только лишь ухудшить

его

благосостояние. Такая характеристи-

ка

точки спроса называется

2-м

законом

Госсена.

Пример

Найдем

точку

спроса

потребителя

функцией

полезности

«(*,'.

)

\/*Г^*2~'

Имеем

Эй/Эх,

{ъ№{*\)>

/*Г/(

1/*Г>>

значит

имеем

систему

уравнений:

(Эи/1Ц

)/(Эи/Эх

)=р

}

/Р

/>i*i+/»

или

<V*T/<

V*T»/

(

V*T/<

fa^PifPv

[PiXi+PiX^Q.

Окончательно;

{XZ/X^PI/PV

x^p

= Q,

т.е.

*,*«

Q/ед,

'«0/(2Р

ЗАДАЧИ

При

ценах

доходе

найти (геометрически

аналитичес-

ки)

точку спроса

для

функции полезности:

а)

н(х

)

min

{*,,

2х

};

б)

u(x

)

2х,

Зх

/'ewewMe.

а)

Функция

«<*.,

х)

min

{.v

означает,

что

излишки

пер-

вого

или

второго товара сверх

отношения

2; 1 не

приносят пользы

потребителю.

Он

получает

ббльшую

пользу только

при

увеличении

обоих

товаров

пределах сохранения пропорции

2:1.

Товары

с та-

кой

функцией полезности называются взаимодополнительными

(на-

пример,

чай

сахар).

Геометрическое решение задачи нахождения

точки

спроса изображено

на

рис.

1, а.

Аналитическое решение

со-

стоит

решении системы:

hiXi+pyX^Q,

\*1

я2

*2*

Ее

решение есть

*.'

Q/(2/>,

ft)»

2<У(2л

+ ft)-

б)

Геометрическое

решение

изображено

на

рис.

£»

--при

Vft

< 2/3 и

рис.

при

р>,

2/3.

На

рис.

Сточка

спроса

Расположена

вершине.

бюджетного

множества,

на

рис.

вершине

В.

139

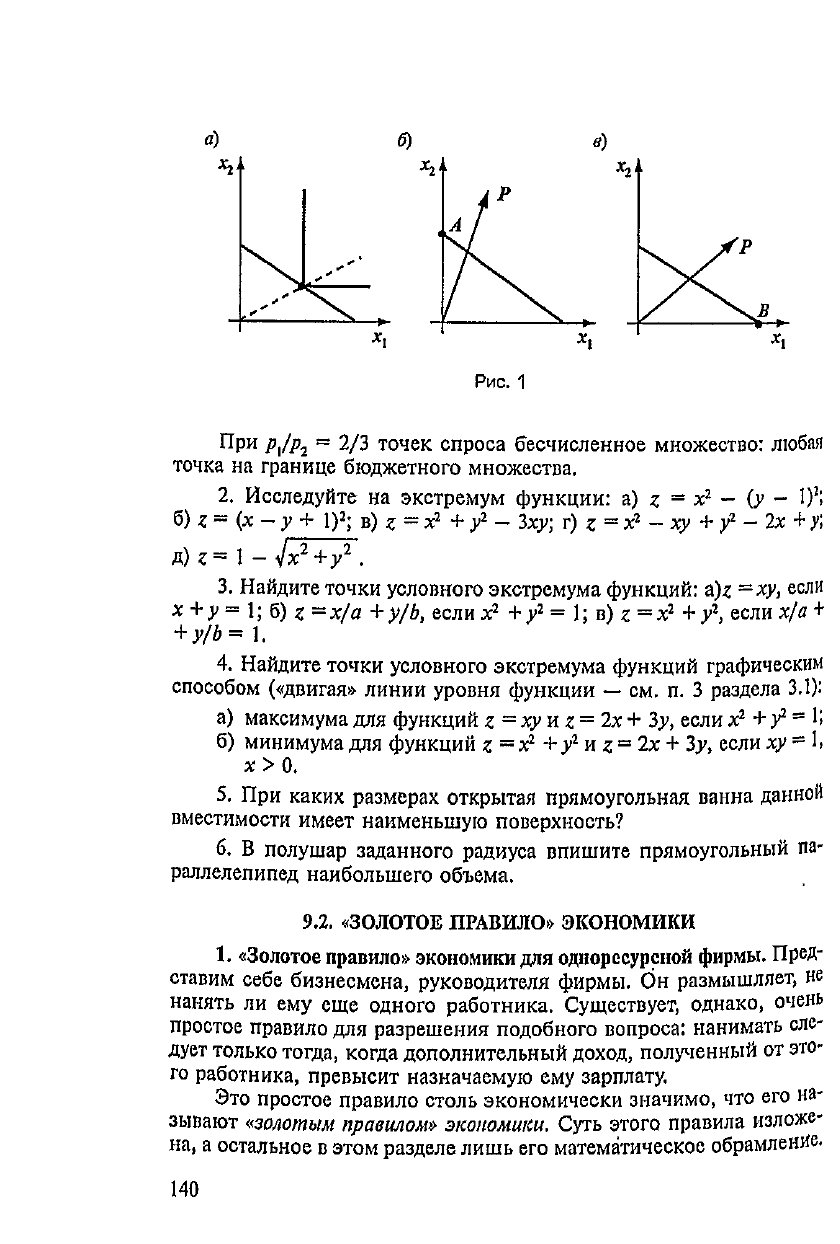
Рис.

При

/),/р

2/3

точек спроса

бесчисленное

множество:

любая

точка

на

границе бюджетного множества.

Исследуйте

на

экстремум функции:

a) z = х

- (у -

;

5)z=

(x-y+

;

в)

z^tf

Зху;

г)

z=x

+у

-2х+У,

Д)

Ух

Найдите точки условного экстремума функций:

а)я

—лу,

если

x+j>

= 1; б)

х/д

+у/Ь,

если

= 1; в) z =

еслих/д

y/b=l.

Найдите точки условного экстремума функций

графическим

способом

(«двигая»

линии уровня функции

— см. п. 3

раздела

3.1):

а)

максимума

для

функций

ху и z

2х

Зу,

если

.х

б)

минимума

для

функций

~х

+у

и z-

3^,

еслиху-Ь

х>0.

5. При

каких размерах открытая прямоугольная ванна

данной

вместимости имеет наименьшую поверхность?

полушар заданного радиуса впишите прямоугольный

па-

раллелепипед наибольшего

объема.

9.2. «ЗОЛОТОЕ

ПРАВИЛО»

ЭКОНОМИКИ

«Золотое правило» экономики

для

одноресурсной

фирмы. Пред-

ставим

себе

бизнесмена,

руководителя фирмы.

Он

размышляет,

не

нанять

ли ему еще

одного работника. Существует, однако,

очень

простое

правило

для

разрешения подобного вопроса: нанимать сле-

дует только тогда, когда дополнительный доход, полученный

от

это-

го

работника, превысит назначаемую

ему

зарплату.

Это

простое правило столь экономически

значимо,

что его на-

зывают

«золотым

правилом»

экономики.

Суть этого правила

изложе-

на,

остальное

этом

разделе

лишь

его

математическое обрамление.

140

применении

одноресурсной фирме

это

правило было изло-

жено

в п. 3

раздела

6.1.

Кратко повторим

основное.

Предположим,

фирма выпускает один товар

и его

количество

обозначим

.у.

Используется только один ресурс. Фирма

полностью

характеризуется

своей производственной функцией

Дх)

—

зави-

симостью

объема выпускаемого товара

от

объема затраченного

ре-

сурса

х.

Предполагается,

что

производственная функция удовлетворяет

двум

аксиомам:

хотя

бы на

части

ее

области

определения,

называемой эко-

номической

областью

Е, эта

функция

неубывающая,

этой

области производная

F'(x)

неотрицательна.

Она

называется

предельным продуктом;

существует выпуклое подмножество

экономической обла-

сти,

для

которой подмножества

{х е

f(x)

а}

также

вы-

пуклы

для

всех

а. В

этом подмножестве

вторая

производная

неположительна.

Остановимся

на

экономическом содержании этих двух аксиом.

Первая

аксиома утверждает,

что

производственная функция

отражает

бесспорное

и в то же

время

тривиальное

утверждение:

мало-мальски

разумной экономике

увеличение

затратно

может при-

вести

уменьшению выпуска.

Из

второй аксиомы поясним только экономический смысл тре-

бования

неположительности второй производной.

Это

свойство

на-

зывается

экономике

законом

убывающей

отдачи

или

убывающей

до-

ходности:

по

мере увеличения объема затраченного

ресурса,

начиная

некоторого момента (при входе

область

Л)

начинает уменьшать-

ся

предельный

продукт.

Классическим

примером

этого закона явля-

йся

добавление

все

большего

большего количества труда

произ-

водство

зерна

иа

фиксированном участке земли.

дальнейшем

будем считать,

что

производственная

ФУНКЦИЯ

имеет

необходимые производные

удовлетворяет обеим аксиомам

всей

области определения.

„„„„„„

Пусть

цена единицы

ресурса

и v -

цена

единицы

выпуска-

емого

товара.

Следовательно,

прибыль

являющаяся

ито_гефун^

№ей

х (и

цен,

но они

считаются постоянными), есть

Щх)

(X)

~-px

Следовательно, приходим

задаче фирмы

Щх)

-»

max,

х>0.

Приравнивая

производную

функции

W(x)

нулю, получим:

Г(х)-р/у.

141