Малков П.Ю. Количественный анализ биологических данных: Учебное пособие
Подождите немного. Документ загружается.


20
53 особей большого трубконоса (см. стр. 14 и 15). Обозначим ус-
ловную среднюю величину как M'. Уменьшим значение вариант на
36.0 мм, получаем:
1.4
53
6.215
53
6.65.712.795.496.62.20
53
6.615.5134.4183.3152.231.1201
≈=
++++++
=
=
⋅
+
⋅
+
⋅
+
⋅
+
⋅
+
⋅
+
⋅
=
′
M
.
Отсюда средняя длина предплечья большого трубконоса, судя
по данной выборке, равна М = 4.1+36 = 40.1 мм.
3.2. Показатели вариации
Средняя величина, как и всякий статистический параметр, ха-
рактеризует лишь одно из свойств анализируемого явления и иг-
норирует другие, в частности, она не отражает такое важнейшее
свойство, как изменчивость. В качестве модели изменчивости при-
знака нередко применяется простейший показатель, основанный
на крайних (минимальном min и максимальном max) значениях,
получивших название лимитов (limit). В биологии лимиты относи-
тельно широко используются в определительных таблицах с це-
лью упрощения идентификации видов (подвидов). Кроме того,
иногда рассчитывают разность между крайними значениями вари-
ант: x
max
- x
min
или отношение этих величин друг к другу: x
max
/
x
min
.
Существенный недостаток подобных показателей - это их зави-
симость исключительно от крайних, наименее типичных значений
и полное игнорирование прочих вариантов. Для иллюстрации это-
го рассмотрим два простейших вариационных ряда:
Ряд 1 Ряд 2
x
1
1 2 3 4 5 x
2
1 2 3 4 5
f
x
1 2 8 2 1 f
x
1 4 4 4 1
Нетрудно заметить, что оба ряда полностью совпадают по
средней величине, числу наблюдений и лимитам (M = 3; n = 14;
x
min
=1; x
max
=5), и тем не менее первый вариационный ряд явно
отличается меньшим разбросом.
В связи с этим для оценки изменчивости признаков предложен
ряд параметров, у которых точкой отсчёта для измерения рассея-
ния отдельных вариантов служит средняя величина. Из таких па-
раметров в практической работе наиболее широко применяется
среднее квадратическое или стандартное отклонение (термин
введен Пирсоном в 1894 году), представляющее собой следующее
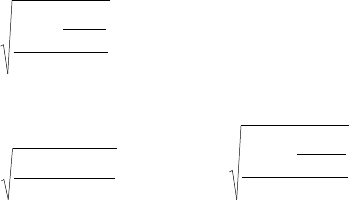
соотношение:
1
)(
2
−
−Σ
=
n
Mx
x
x
σ
(3.3.).
21
Из этой формулы видно, что при вычислении стандартного от-
клонения учитывается разница между отдельным вариантом серии
наблюдений и их средней величиной: (x - M
x
). При этом каждое
отклонение возводится в квадрат для того, чтобы нивелировать
равновесие отрицательных и положительных отклонений вариан-
тов от средней, так как Σ(x - M
x
) = 0. Математическое обоснование
формулы приводится в [Баврин, 2002].
Считается, что вычисление стандартного отклонения прямым
путём довольно трудоёмко, так как для этого необходимо из каж-
дого значения x вычитать среднюю величину M
x
, возводить все
полученные разности в квадрат, а затем суммировать их [Бейли,
1962]. Поэтому иногда вместо этого удобнее использовать форму-
лу:
(
)
1
2
2
−
Σ
−Σ
=
n
n
x
x
σ
(3.4.).
В случае если по данным наблюдений построен вариационный
ряд формулы (3.3.) и (3.4.) приобретают вид соответственно:
(
)
1
2
−
−Σ
=
n
Mxf
x
σ
(3.5.),
(
)
1
2
2
−
Σ
−Σ
=
n
n
fx
fx
σ
(3.6.).
Стандартное отклонение очень удобная и понятная характери-
стика, которая выражается в тех же единицах измерения, что и
анализируемый признак. Одно из важнейших его свойств заклю-
чается в том, что, зная среднюю величину и стандартное отклоне-
ние в отдельной выборке, можно с определённой уверенностью
судить о генеральной совокупности, из которой взята эта выборка.
Из теории статистики и эмпирических исследований известно, что
выборка, репрезентативно отражающая генеральную совокуп-
ность, как правило, обладает следующими свойствами:
ü в пределах M ± 1σ сконцентрировано 68.3 % вариантов
генеральной совокупности;
ü в пределах M ± 2σ сгруппировано 95.5 % вариантов генераль-
ной совокупности;
ü в пределах M ± 3σ расположено 99.7 % вариантов генераль-
ной совокупности.
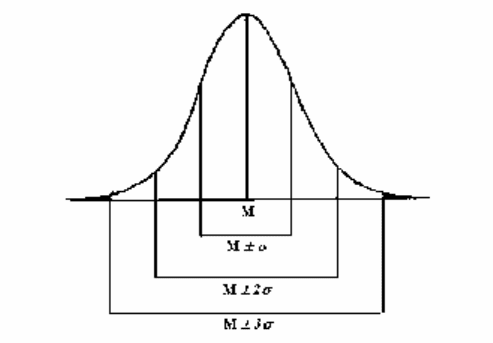
22
Рис. 4. Диаграмма нормального распределения.
Указанная закономерность, получившая название нормально-
го распределения, является одной из ключевых в вариационной
статистике и её следует запомнить. Термин “нормальное распре-
деление” введен в биологическую лексику Гальтоном в 1889 году.
Однако ещё задолго до этого оно было хорошо известно математи-
кам, которые это распределение часто называют законом Гаусса –
Лапласа. Как видно из рисунка 4, нормальное распределение или
распределение Гаусса - Лапласа графически может быть отобра-
жено симметричной колоколообразной кривой, вершиной которой
является свойственная генеральной совокупности средняя вели-
чина. Возможность вероятностной оценки генеральной средней
будет рассмотрена ниже (раздел 3.3.).
Подчинённость самых различных объектов нормальному рас-
пределению требует хотя бы поверхностного осмысления, так как
принятие этого закона “на слово” может завести нас в область ме-
тафизики. Рассмотрим вначале пример, не относящийся к области
биологии. Представим рабочего, изготавливающего детали опре-
деленного размера. Логично предположить, что большая часть из
произведённых им деталей будет совпадать или незначительно
отклоняться от требуемой величины. Однако, каков бы ни был на-
вык у данного рабочего, он человек и ему свойственно делать
ошибки. При этом, чем больше отклонение от необходимого раз-
мера детали, тем ниже вероятность того, что рабочий произведёт
такую деталь. Само собой разумеется, у другого рабочего (пред-
положим менее опытного) вариабельность произведённых деталей
будет отличаться, однако общий принцип при этом останется не-
изменным.
23
Чем же обусловлена подчиненность многих количественных
признаков такому распределению у животных и растений?
Известно, что количественные признаки, в отличие от боль-
шинства качественных, контролируются множеством генов, часть
из которых оказывает взаимно противоположное, компенсирую-
щее действие. В результате фенотип по таким признакам, в об-
щем, стремится к некоторому уравновешенному, характерному для
большинства особей, среднему состоянию. Однако, так как соот-
ношение аллелей в локусах зависит от чисто случайных, стохасти-
ческих процессов, практически в каждой популяции существует
вся гамма переходов от относительно малой, до относительно
большой величины того или иного количественного признака. Оп-
ределённое воздействие на организм оказывает и внешняя среда.
Распределение вариантов в конкретной выборке далеко не все-
гда полностью совпадает с нормальным. Наиболее типичными не-
соответствиями являются: асимметрия, то есть смещение вершины
распределения относительно среднего значения, и эксцесс - вы-
раженная плоско- или островершинность распределения [Лакин,
1990 и др.]. Однако в большинстве случаев всё же можно исполь-
зовать тесты, основанные на предположении о нормальности рас-
пределения. Дело в том, что при возрастании объёма выборки
форма выборочного распределения средней арифметической при-
ближается к нормальной, даже если распределение исследуемых
переменных не является таковым [Электронный …, 1999 и др.].
Отсюда следует, что для статистического анализа всегда предпоч-
тительнее иметь многочисленную выборку (n>30).
Несоответствие нормальному распределению может быть вы-
звано не только спецификой варьирования признака, но и качест-
венной неоднородностью выборки. Типичный пример такого рода
представлен на рисунке 5, где проиллюстрирована изменчивость
длины тела с хвостом 25 особей серебристого карася, отловлен-
ных в 1985 году на Манжерокском озере (Северный Алтай). На
гистограмме хорошо видно, что форма распределения имеет двух-
вершинный облик. Левая вершина распределения соответствует
возрастным категориям: от сеголеток до двухгодовалых, а правая
– трёхлетним особям. Таким образом, несовпадение с нормальным
распределением, в данном случае, явно обусловлено возрастной
изменчивостью анализируемого материала. В этом и подобных
случаях первоначальную выборку целесообразнее разбить на ка-
чественно более однородные группы.
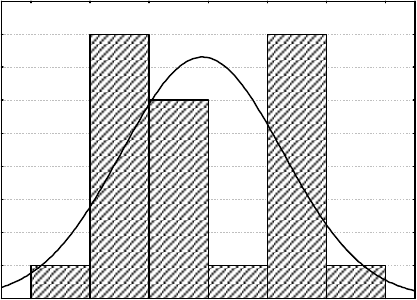
24
0 50 100 150 200 250 300
Длина, мм.
0
1
2
3
4
5
6
7
8
9
Абсолютная частота
Рис. 5. Распределение длин тела (с хвостом) 25 особей серебри-
стого карася.
Практическое применение стандартного отклонения разберём
на примере сведений о массе тела самцов алтайской мышовки
Sicista napaea Hollister в условиях среднегорья Северного Алтая.
Полученные материалы собраны в разные годы, но в один и тот же
сезонный период, студентами Г-АГУ, при прохождении летних по-
левых практик по зоологии позвоночных. Результаты взвешива-
ний, с точностью до 0.1 гр., оказались следующими: 11.0, 9.3,
11.8, 9.8, 9.4, 9.4, 16.0, 9.3, 9.1, 10.8, 10.8, 8.6, 10.4, 12.0, 15.5,
9.7, 8.6, 8.7, 8.1, 10.7, 9.2, 8.3, 9.1, 7.7. Имеющаяся выборка не-
велика по объёму (n = 24) и на её основании некорректно судить
о сезонной изменчивости массы тела. Поэтому, не вдаваясь в де-
тали, попытаемся получить лишь общее представление об измен-
чивости этого признака в пределах интересующей нас территории.
Для вычисления стандартного отклонения воспользуемся форму-
лой (3.4.), в которой фигурируют такие выражения как: Σx
2
и
(Σx)
2
. Несмотря на сходство в их написании эти величины различ-
ны по своей сути, первая - представляет собой сумму квадратов
значений вариантов, вторая - квадрат суммы значений вариантов.
Соответственно:
Σx
2
= 11.0
2
+ 9.3
2
+ 11.8
2
+ 9.8
2
+ 9.4
2
+ 9.4
2
+ 16.0
2
+ 9.3
2
+
9.1
2
+ 10.8
2
+ 10.8
2
+ 8.6
2
+ 10.4
2
+ 12.0
2
+ 15.5
2
+ 9.7
2
+ 8.6
2
+
8.7
2
+ 8.1
2
+ 10.7
2
+ 9.2
2
+ 8.3
2
+ 9.1
2
+ 7.7
2
= 121 + 86.49 +
139.24 + 96.04 + 88.36 + 88.36 +256 + 86.49 + 82.81 + 116.64 +
116.64 + 73.96 + 108.16 + 144 + 240.25 + 94.09 + 73.96 + 75.69
+ 65.61 + 114.49 + 84.64 + 68.89 + 82.81 + 59.29 = 2563.91;

25
(Σx)
2
= (11.0 + 9.3 + 11.8 + 9.8 + 9.4 + 9.4 + 16.0 + 9.3 + 9.1 +
10.8 + 10.8 + 8.6 + 10.4 + 12.0 + 15.5 + 9.7 + 8.6 + 8.7 + 8.1 +
10.7 + 9.2 + 8.3 + 9.1 + 7.7)
2
= 243.3
2
= 59194.89.
Подставляя вычисленные значения в формулу (3.4.) получаем:
σ =
124
24
89.59194
91.2563
−
−
=
23
45.246691.2563 −
=
23
46.97
=
=
24.4
≈ 2.1 гр.
После нахождения средней массы тела прямым и очевидным
способом (формула 3.1.) - M=10.1 гр. можно, с определённой до-
лей вероятности, приступить к выяснению свойств генеральной
совокупности, то есть, в нашем случае, к изменчивости массы тела
самцов алтайской мышовки, обитающих в среднегорном поясе Се-
верного Алтая. Принимая во внимание, что варьирование массы
тела в этом случае приближается к нормальному, можно утвер-
ждать, что в данных природных условиях около 95 % самцов дан-
ного вида имеют массу тела от 5.9 до 14.3 гр., или, иначе говоря,
лишь 1 из 20 самцов теоретически может выйти за пределы ука-
занных величин.
Стандартное отклонение обладает рядом математических
свойств, часть из которых позволяет упростить его вычисление.
Например, если уменьшить (увеличить) все варианты анализируе-
мой выборки на одно и то же число, то стандартное отклонение не
изменится. Для иллюстрации этого обратимся к вариационному
ряду длины предплечья 53 особей большого трубконоса (см. стр.
и ). Как и в случае с вычислением средней величины, уменьшим
центры классовых интервалов на 36.0 мм. Полученные значения
принимаем за условные центры классовых интервалов x'. Вычис-
ляем сумму квадратов отклонений условных центров классовых
интервалов от условной средней величины (M
x
'
= 4.1 мм), как это
показано в таблице 4.
Таблица 4
x' f (x' – m
x
'
) (x' - m
x
' )
2
f (x' - m
x
'
)
2
0 1 - 4.1 16.81 16.81
1.1 2 - 3.0 9.00 18.00
2.2 3 - 1.9 3.61 10.83
3.3 15 - 0.8 0.64 9.60
4.4 18 0.3 0.09 1.62
5.5 13 1.4 1.96 25.48
6.6 1 2.5 6.25 6.25
сумма: 88.59

26
Отсюда (см. формулу (3.3.)) σ =
52
59.88
=
7.1
= 1.3 мм.
Рассчитанная таким способом величина стандартного отклоне-
ния предметно интерпретируется так же, как и в примере с массой
тела самцов алтайской мышовки.
Практическое применение σ в биологических науках не ограни-
чивается лишь сферой морфологических и анатомических иссле-
дований. Этот показатель хорошо зарекомендовал себя при
упорядочивании представлений о сезонных явлениях в природе
[Фенологические …, 1982], о распределении и динамике числен-
ности организмов, а также при решении вопросов селекции и ге-
нетики.
Таким образом, стандартное отклонение представляет собой
одну из наиболее обоснованных и эффективных описательных
статистик. Однако, если необходимо сопоставить изменчивость
признаков, представленных в разных единицах измерения (на-
пример, мм. и гр.) этот показатель использовать нельзя, так как
он измеряется в тех же величинах, что и средняя величина. Кроме
того, одно и то же значение стандартного отклонения (например, σ
= 2) может указывать как на очень малую (М = 100), так и на
очень большую изменчивость (М=5). Для сравнения изменчивости
признаков в таких случаях лучше применять коэффициент ва-
риации, равный процентному отношению стандартного отклоне-
ния к средней арифметической величине, то есть:
M
C
v
%100
⋅
=
σ
. (3.7.)
Специальными исследованиями установлено, что изменчивость
одного и того же признака, выраженная коэффициентом вариа-
ции, может отличаться как у различных видов, так и у разных по-
пуляций в пределах одного вида, причём эти отличия зачастую не
случайны и имеют направленный характер. Это послужило осно-
вой для формирования единых методологических позиций при
изучении индивидуальной и эволюционной изменчивости организ-
мов [Яблоков, 1966; Смирнов, 1971 и др.]. Интересные результа-
ты, в этом плане, получены, например, Л. Н. Добринским [1981],
который на основе анализа большого материала по изменчивости
морфофизиологических признаков птиц показал, что у некоторых
видов степень вариабельности интерьерных признаков четко от-
личается у северных и южных популяций, тогда как изменчивость
индексов ряда внутренних органов не совпадает с географически-
ми градиентами. Последнее объясняется функциональным значе-
нием внутренних органов (например, в любой географической
зоне требуется строго определённое соотношение массы тела и
массы летательной мускулатуры у всех слагающих популяцию осо-
бей).
27
Коэффициент вариации находит применение и в селекционной
работе [Федоров, 1957; Снедекор, 1961; Мацеевский, Земба, 1988
и др.]. Например, при сравнении двух сходных по продуктивности
и качественным показателям сортов, предпочтение должно быть
отдано тому из них, который при равных условиях обладает мень-
шей изменчивостью.
3.3. Ошибка выборочной средней
Из предыдущих разделов должно быть ясно, что параметры M и
σ вычисляются исключительно на основе исходной серии наблю-
дений и их точность зависит от того, насколько полно анализи-
руемая выборка представляет генеральную совокупность.
Предположим, что при сборе первичного материала выбрана
вполне адекватная методика, чётко выдержан принцип репрезен-
тативности, а также не допущено ошибок в математических вы-
числениях. Будут ли полученные статистические оценки совпадать
с истинными, свойственными генеральной совокупности? Вообще
говоря, если мы не знаем этих "истинных" значений, то с полной
уверенностью на поставленный вопрос нельзя ответить утверди-
тельно. Для того, чтобы убедиться в этом, достаточно взять из лю-
бой природной популяции несколько выборок, проанализировать
их и сопоставить результаты между собой. В большинстве случаев
полученные оценки будут различны.
Совершенно очевидно, что наилучшим методом для повышения
точности оценок генеральной совокупности по данным выборки
является увеличение объёма наблюдений. Иными словами, ошибка
статистического параметра, вычисленного по данным выборки,
будет тем меньше, чем больше число наблюдений, составляющих
эту выборку. Такое свойство выборочных статистик позволило
разработать ряд показателей, позволяющих оценивать вероятные
пределы, в которых может находиться значение соответствующего
генерального параметра. В частности, для вычисления статистиче-
ской ошибки выборочной средней M используется следующая
формула:
n
m
σ
±=
, (3.9.)
где m - ошибка средней величины. Остальные обозначения понят-
ны из предыдущих разделов.
Ошибка средней (точнее стандартная ошибка) в случае нор-
мального распределения подчиняется той же закономерности, что
и стандартное отклонение. Отличие состоит в том, что стандартное
отклонение отражает разброс всех вариантов относительно сред-
ней, а стандартная ошибка показывает пределы, в которых, с из-
вестной вероятностью, может располагаться средняя величина.
Отсюда, в интервале M ± 1m средняя величина генеральной сово-

28
купности может находиться с вероятностью 68.3 %, в интервале
M ± 2m - с вероятностью 95.5 %, а в пределах M ± 3m - с вероят-
ностью 99.7 %.
Процедуру вычисления стандартной ошибки выборочной сред-
ней рассмотрим на примере сведений о длине тела самцов полё-
вок-экономок Microtus oeconomus Pall., обитающих в среднегорьях
Северного Алтая. Предварительные вычисления, идентичные вы-
числениям по массе тела алтайских мышовок, показали, что при n
= 34 длина тела характеризуется: M = 101.6 мм, σ = 15.0 мм.
Подставляем известные значения в формулу (3.9.):
ммm 57.2
83.5
0.15
34
0.15
===
.
В результате проведённых вычислений мы, конечно, не узнали
"истинное" значение средней длины тела у самцов рассматривае-
мой популяции, однако теперь с 95 % вероятностью можно утвер-
ждать, что оно находится в пределах 101.6 ± 2⋅2.57 мм, то есть от
96.5 до 106.7 мм.
Вычисленные таким способом доверительные интервалы будут
эффективно отражать анализируемое явление, когда распределе-
ние исходных вариантов соответствует нормальному. Однако, если
серия наблюдений не велика по объёму (n≤30), то естественно
ожидать, что в ней не будут представлены те варианты, которые
сильно отклоняются от среднего значения. В результате, это мо-
жет приводить к неверной оценке.
Метод нахождения доверительных интервалов в случае анализа
небольших выборок найден английским химиком и статистиком
Госсетом. Им же разработана специальная таблица, так называе-
мых, значений t (приложения табл. 1). Величина t показывает, во
сколько раз необходимо увеличить стандартную ошибку выбороч-
ного статистического параметра для того, что бы при определен-
ном уровне вероятности судить о тех пределах, в которых
располагается генеральное значение.
Использование этой таблицы не требует особых вычислений,
поскольку величина t напрямую зависит лишь от уровня вероятно-
сти P и числа степеней свободы ν. В большинстве биологических
исследований принимают P=0.95 (то есть 95 случаев из 100), в
наиболее ответственных случаях - 0.99 или 0.999. Число степеней
свободы ν, при нахождении доверительных интервалов для M,
равно: ν = n - 1.
Рассмотрим пример. Длина тела самок полёвок-экономок из
среднегорий Северного Алтая характеризуется следующими выбо-
рочными показателями: n = 10, M = 105.7 мм, σ = 16.7 мм. Вычис-
лим стандартную ошибку выборочной средней величины:
.29.5
10
7.16
ммm ==
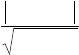
29
В таблице 1 приложений находим, что при P = 0.95 или 95 % и
при ν = 10 – 1 = 9 величина t равна 2.26. Следовательно, с веро-
ятностью P=0.95 или 95 % можно утверждать, что в обследован-
ной популяции средняя длина тела у самок Microtus oeconomus
Pall., находится между 105.7-2.26⋅5.29 = 93.7 мм и
105.7+2.26⋅5.29 = 117.7 мм.
3.4. Сравнение средних величин
Как в научно-исследовательских работах, так и при решении
ряда практических задач анализ отдельных выборок редко явля-
ется конечной целью. Очень часто приходится сравнивать эти вы-
борки между собою и тогда закономерно встает вопрос, -
достоверны ли наблюдаемые отличия между выборками или они
обусловлены лишь какими-то случайными причинами (например,
недостатком данных)? В том случае, когда сравниваемые вариаци-
онные ряды обособлены друг от друга настолько, что наименьшее
значение признака в одной из выборок превосходит наибольшее
значение того же признака в другой выборке можно без специаль-
ного анализа принять, что они существенно различны. Однако не-
обходимость сравнения полностью изолированных вариационных
рядов редко встречается на практике. Чаще всего сопоставляемые
выборки, по значению своих максимальных и минимальных вари-
ант, в той или иной мере заходят друг за друга. Такое захождение
носит название “трансгрессия”. Степень трансгрессии может
быть различной: от частичного до полного поглощения одного ва-
риационного ряда другим.
Вопрос о достоверности отличия двух сравниваемых выборок
обычно решается при помощи сравнения их средних величин. При
этом исходят из простого правила, которое заключается в том, что
две выборки, вероятно, различны, если разница между их средни-
ми величинами (M
1
– M
2
) более чем в два раза превосходит сумму
их средних ошибок (m
1
+ m
2
), и почти наверняка различны, если
она превышает сумму средних ошибок более чем в три раза.
Значительно надежнее пользоваться при этом критерием досто-
верности различий (t-критерий), определяемым по формуле:
2
2
2
1
21
mm
MM
t
+
−
=
. (3.10.)
Прямые скобки здесь и далее в тексте показывают, что резуль-
тат вычисления берётся по модулю, то есть без учёта знака.
После вычисления фактической (эмпирической) величины t об-
ращаются к таблице стандартных значений t
st
(приложения табл.
1). Число степеней свободы в данном случае равно n
1
+ n
2
- 2. Ги-
потезу об отсутствии различий между выборочными средними от-
вергают, если фактически установленная величина t превзойдет
