Малков П.Ю. Количественный анализ биологических данных: Учебное пособие

Подождите немного. Документ загружается.

лученные данные о численности видов в пределах фактически об-

следованной площади в дальнейшем, для сопоставимости, пере-

считываются на определённую единицу площади (число

экземпляров /м

, /га или /км

). В геоботанических работах ширина

трансекта может быть сведена до одной линии [Быков, 1967]. Для

подсчета пресмыкающихся и земноводных обычно используют

трансект шириной 3 метра (1.5 метра справа и слева от учётчика)

[Динесман, Калецкая, 1952]. В условиях разреженного травяни-

стого покрова этот метод может использоваться и для подсчёта

мелких членистоногих - цикадовых, клопов, мелких двукрылых и

перепончатокрылых, жуков, клещей, пауков и т. п., но тогда ши-

рина трансекта составляет 0.25 - 1 метр [Второв, 1968; Злотин,

1975 и др.].

Дневных бабочек учитывают обычно на полосе шириной 3 мет-

ра [Yamomoto, 1975; Pollard, 1977; Сергеев, Дубатолов, 1988; Ду-

батолов, Костерин, 1999 и др.]. Однако более эффективно

рассчитывать ширину трансекта для каждого вида отдельно по

удвоенной средней дальности его обнаружения [Малков, 1994;

Малков, Малков, 1999; Бондаренко, 1999, 2003]. Для вычисления

обилия в таком случае можно использовать формулу:

, (2.1.)

где x

- обилие i вида в пересчете на 1 гектар, n

- число зарегист-

рированных особей i вида, k

- средняя дальность обнаружения

i вида в метрах, L - длина маршрута в километрах.

При учёте птиц особи регистрируются как путём визуального

наблюдения, так и на слух, поэтому их лучше разделять на три

группы по дальности фактического обнаружения: 1) птицы, обна-

руженные близко - до 25 м от учётчика; 2) недалеко - в 25 - 100 м

от учётчика; 3) далеко - от 100 до 300 м от учётчика.

Вычислять обилие проще с помощью формулы:

днб

31040

, (2.2.)

где x

- обилие i вида в пересчете на 1 км

, б - число особей i вида,

замеченных близко, н - недалеко, д - далеко, L - длина маршрута

в километрах [Равкин, 1967].

При изучении насекомых, обитателей травяного яруса, нередко

применяются различные модификации метода кошения энтомо-

логическим сачком. Наиболее известная его разновидность -

учёт на время. Для этого в исследуемом местообитании насекомые

отлавливаются стандартным сачком (диаметром 40 см) в течение

определенного промежутка времени с последующим пересчетом

на 1 час [Бей-Биенко, 1932; Сергеев, 1986; Пшеницына и др.,

1993].

Скрытно живущих и ночных животных обычно приходится от-

лавливать в разнообразные ловушки.

2.2. Техника измерений и округлений

На первом этапе изучения морфологии организмов неизбежно

встает вопрос о том, что и как измерять, чтобы наилучшим обра-

зом отразить специфику объекта исследования. Совершенно оче-

видно, что на этот вопрос нет и не может быть универсального

ответа, однако по некоторым, наиболее хорошо изученным таксо-

номическим группам животных морфологические промеры стан-

дартизированы. Так, у мелких млекопитающих измеряют длину

тела, хвоста, уха, длину ступни задней ноги, а также определен-

ные параметры черепа [Бобринский и др., 1965; Юдин, 1971; По-

пов, 1977], у птиц - длину крыла, хвоста, клюва и плюсны

[Иванов, Штегман, 1964] и т.п. Перечисленные признаки важны

для определения, поэтому их наносят на этикетки, которые хра-

нятся вместе с коллекционными экземплярами. Для решения бо-

лее специальных задач, например, при выяснении возрастной,

половой, географической изменчивости таксона имеет смысл де-

лать все возможные измерения и уже в ходе последующего анали-

за выбирать наиболее информативные признаки. При описании

собранного материала в научных статьях, дипломных и курсовых

работах всегда необходимо подробно оговаривать, каким образом

проводили тот или иной замер, допустим: "ширина крыла - рас-

стояние от кистевого сустава до вершины первого второстепенно-

го махового пера".

При изучении морфологии организмов вовсе необязательно де-

лать упор на достижение максимально возможной точности, а

нужно исходить лишь из соображений целесообразности. Классики

числовой таксономии Дж. Симпсон и Э. Роэ [1939] показали (цит.

по: [Майр и др., 1956]), что, если в руках исследователя имеется

относительно большая выборка, в качестве единицы измерения

следует принимать

разницы между самым крупным и самым

мелким экземпляром в выборке. Например, если значения вариант

укладываются в ряд от 10 до 12 мм, измерения следует проводить

с точностью до 0.1 мм ((12 – 10) / 20 = 0.1); если от 40 до 50 мм -

с точностью до 0.5 мм ((50 –40) / 20 = 0.5); если же пределами

измерений служат 70 и 90 мм, то измерения следует вести в целых

миллиметрах и т.п.

В ходе вычисления обобщающих статистических показателей

постоянно приходится сталкиваться с необходимостью округлений.

Существуют разнообразные способы округления и, в принципе,

можно использовать любой из них, важно лишь на протяжении

всего хода работ следовать одному и тому же правилу. Обычно

поступают следующим образом: если за последней сохраняемой

цифрой следуют цифры <5, то они отбрасываются, если ≥5, то по-

следняя цифра увеличивается на единицу.

2.3. Отношения и индексы

Абсолютные размеры тела, как правило, весьма изменчивы и

зависят от возраста, условий существования и т.п., однако их от-

ношения могут оставаться сравнительно постоянными. Для выяв-

ления относительных размеров (индексов) различных частей тела

можно пользоваться формулой:

или

(2.3.),

где I

- индекс меньшего по величине признака, I

- индекс боль-

шего по величине признака, x – значение меньшего признака, y –

значение большего признака. В тех случаях когда признаки x и y

примерно равны по величине, возможна ситуация, при которой

отдельные значения признака y могут оказаться меньшими.

В качестве примера приведем процедуру вычисления относи-

тельной длины хвоста, по двум видам кротов: обыкновенному

Talpa europea L. и сибирскому Asioscalops altaica Nikolsky (табл. 1).

Определяем индекс относительной длины хвоста:

для обыкновенного крота

189.0

133

2.25

хвоста

для сибирского крота

176.0

153

0.27

хвоста

Таблица 1

Средние величины некоторых морфологических параметров кро-

тов T. europea (I) и A. altaica (II), мм

(по данным Б. С. Юдина [1971])

Признак I II

Длина тела с головой 133.6 153.8

Длина хвоста 25.2 27.0

Сравнивая полученные результаты, приходим к выводу, что

обыкновенный крот, имея меньшие абсолютные размеры, отлича-

ется бόльшей относительной длиной хвоста.

Отношения широко используются не только для сравнительных

целей, но и для определения слабо различимых видов. Так, на-

пример, два вида саранчовых - итальянский прус Calliptamus

italicus L. и светлокрылый прус C. abbreviatus Ikonn., внешне

очень похожи и их идентификация могла бы представлять опреде-

ленные трудности, однако оказалось, что они без проблем отли-

чаются по отношению длины надкрылий к длине заднего бедра

[Ванькова, 1998].

2.4. Вариационные ряды

Как уже отмечалось, подвергая варьирующий признак стати-

стическому анализу, мы, в сущности, отвлекаемся от конкретного

содержания и оперируем лишь абстрактными значениями. При

этом смысл анализа сводится к выявлению общих свойств гене-

ральной совокупности, отраженных в конкретной выборке. В связи

с этим уже на самых ранних этапах статистической обработки мо-

жет оказаться полезной группировка первичных данных. Группи-

ровка считается успешной, если удовлетворяет следующим

требованиям [Тьюки, 1981].

1. В ходе группировки не теряется важная информация.

2. В результате группировки первичные данные принимают бо-

лее компактную форму, что в свою очередь облегчает воспри-

ятие и последующие вычисления.

Во многих случаях этим положениям соответствует метод ва-

риационных рядов, показывающий, каким образом числовые зна-

чения признака связаны с их повторяемостью в данной выборке

[Плохинский, 1970; Лакин, 1990 и др.]. Вариационные ряды под-

разделяются на интервальные и безынтервальные. Безынтерваль-

ный вариационный ряд целесообразно строить в тех случаях,

когда разница между минимальным и максимальным значением

вариантов невелика, особенно, если признак варьирует дискрет-

но. Последовательность его построения рассмотрим на примере

данных о числе глазков на 40 клубнях картофеля. Результаты

подсчёта оказались следующие: 7, 9, 5, 11, 9, 7, 8, 5, 8, 7, 7, 10,

6, 7, 5, 7, 8, 6, 5, 7, 7, 6, 5, 6, 4, 5, 5, 10, 5, 8, 7, 6, 7, 5, 7, 7, 6, 5,

6, 6. Находим минимальное и максимальное значение признака

min

= 4, x

max

= 11). Записываем все возможные, в пределах ми-

нимального и максимального, значения, и указываем, как часто

принимает ту или иную величину анализируемый признак x. В об-

щем случае частоты признака обозначаются буквой f (англ.

frequency). Для их подсчета удобно пользоваться условными обо-

значениями: . = 1; . . = 2; : . = 3; : : = 4; : : = 5; : : = 6; : : = 7;

: : = 8; : : = 9; : : = 10; : : . = 11 и т.д.

Вариационный ряд числа глазков на клубнях картофеля (n = 40)

Значение признака x 4 5 6 7 8 9 10 11

Частота признака f

. : : : : : : : : : : : .

1 10 8 12 4 2 2 1

Полученный вариационный ряд полностью соответствует тре-

бованиям, предъявляемым к группировке данных, поскольку пер-

воначальный материал стал более «обозримым», и в результате

простейших преобразований мы сделали явной ранее завуалиро-

ванную информацию. В частности, хорошо видно, что большая

часть значений признака сгруппирована в пределах 5-7 глазков,

тогда как крайние значения вариант встречаются относительно

редко.

Процедуру построения интервального вариационного ряда раз-

берём на материале, собранном студентами Г-АГУ. Измерение дли-

ны предплечья у 53 особей летучей мыши вида большой

трубконос Murina leucogaster Milne-Edwards без учета половой

принадлежности с точностью до 0.1 мм дало следующие результа-

ты: 39.5, 40.4, 38.6, 39.4, 39.5, 40.0, 38.6, 36.0, 39.0, 40.4, 39.5,

42.5, 41.0, 39.6, 41.8, 39.5, 40.0, 39.7, 40.0, 37.5, 42.0, 38.7, 41.5,

40.0, 42.0, 40.0, 41.5, 40.5, 37.6, 40.0, 39.5, 40.7, 40.0, 41.7, 40.0,

41.5, 41.3, 41.2, 39.0, 40.0, 40.0, 42.0, 39.3, 40.5, 39.0, 40.5, 39.5,

40.0, 39.8, 42.0, 41.2, 40.0, 39.5.

Отыскиваем минимальное и максимальное значение признака

min

=36.0, x

max

=42.5). Затем находим величину классового интер-

вала (λ) по формуле:

minmax

−

=λ

, (2.4.)

где k - приблизительное число классов, на которое следует раз-

бить вариацию признака. Значения k приведены ниже (табл. 2).

Как видно из таблицы, более представительные по объёму выбор-

ки следует разбивать на большее число классов. Последнее тре-

бование лишь незначительно сказывается на затратах времени, но

зато сводит к минимуму потерю информации.

Таблица 2

Число наблюдений n Число классов K

20-30 5

30-100 7

100-1000 10 и больше

Подставляя значения в формулу (2.4.), получаем величину

классового интервала (λ=1.1 мм). Принимаем минимальное значе-

ние длины предплечья большого трубконоса (x

min

=36.0) за сере-

дину первого классового интервала. В результате получаем

следующие интервалы 35.5 - 36.6 - 37.7 - 38.8 - 39.9 - 41.0 - 42.1

- 43.2. После уменьшения верхних границ классов на точность из-

мерений (0.1 мм.) и распределения значений вариантов по клас-

сам получаем вариационный ряд (табл. 3).

Таблица 3

Вариационный ряд длины предплечья большого трубконоса

(n=53)

Классовые

интервалы x

35.5-

36.5

36.6-

37.6

37.7-

38.7

38.8-

39.8

39.9-

40.9

41.0-

42.0

42.1-

43.1

Центральная

величина

классового

интервала

36.0 37.1 38.2 39.3 40.4 41.5 42.6

Частота f

1 2 3 15 18 13 1

Для вычисления статистических параметров (см. главу III) ин-

тервальный вариационный ряд трансформируют в безынтерваль-

ный. При этом середину классового интервала принимают за

величину, характеризующую все варианты входящие в этот класс.

Середину каждого классового интервала находят отношением

суммы значений нижней и верхней границы интервала к 2. Отсюда

центральная величина первого классового интервала равна

35.5+36.5/2=36.0, второго - 36.6+37.6/2=37.1, третьего -

37.7+38.7=38.2 и т.д.

2.5. Графическое отображение данных

График (диаграмма) - одно из наиболее эффективных средств

представления данных. Правильно построенный график может

служить мощным инструментом, как для иллюстрации материала,

так и для формирования предварительных гипотез. Неслучайно

графики стали почти обязательным элементом дипломных и кур-

совых работ, многих научных публикаций, основанных на количе-

ственных данных. Более широкое распространение получили

двумерные графики (2 М), в том числе с добавочной осью орди-

нат, поскольку с них удобнее считывать информацию. Из семейст-

ва двумерных графиков наиболее известны точечные диаграммы

рассеяния, линейные графики и столбчатые гистограммы.

Точечные диаграммы рассеяния строят, когда на графике

необходимо сохранить информацию о каждом варианте анализи-

руемой группы данных. В частности, по ним можно установить,

существует ли между определенными признаками зависимость или

они не связаны друг с другом. Кроме того, точечные диаграммы

позволяют быстро определить, перекрывается ли один и тот же

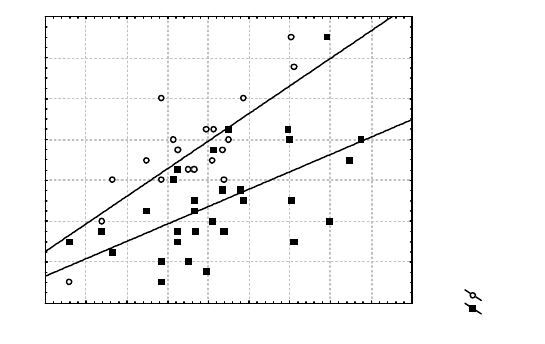
признак у представителей разных выборок. Пример такого графи-

ка приведен на рисунке 1, где отображено соотношение трёх при-

знаков, проанализированных на экспонатах коллекции черепов

алтайской популяции бурого медведя (зоомузей Г-АГУ). Из графи-

ка видно, что длина правого верхнего клыка достаточно равно-

мерно возрастает при увеличении общей длины черепа, тогда как

ширина мозговой капсулы значительно в меньшей степени зави-

сима от этого показателя.

Д_П_В_К

Ш_М_К

Максимальная длина черепа, мм

Длина правого верхнего клыка, мм

Ширина мозговой капсулы, мм

102

106

110

114

118

240 260 280 300 320 340 360 380 400 420

Рис. 1. Точечная диаграмма, показывающая взаимосвязь между

некоторыми краниологическими признаками у представителей ал-

тайской популяции бурого медведя.

На линейных графиках отдельные точки данных соединены

линией. Обычно графики такого типа используются, когда изуча-

ется определенная последовательность значений, причем порядок

этих значений является одним из существенных признаков. Ли-

нейные графики могут быть очень полезными для иллюстрации

изменения какого-либо явления во времени и потому они широко

применяются при изучении суточной, сезонной и вековой динами-

ки численности организмов, для изучения процессов онтогенеза и

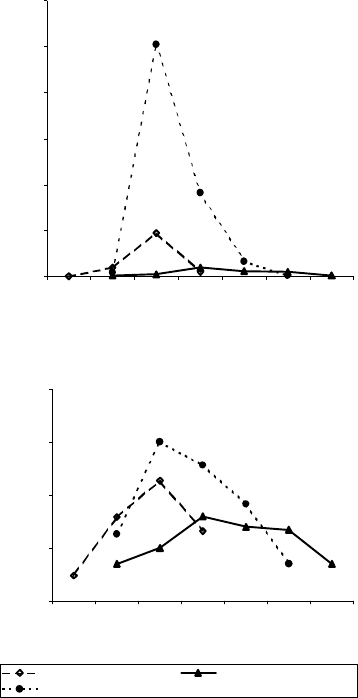
т.п.. В случае, если значения одной или нескольких переменных

изменяются на порядок и более, график предпочтительнее строить

в логарифмическом масштабе [Уильямсон, 1975] (сравните рис. 2

А и 2 Б).

100

120

май_2 июнь_1 июнь_2 июль_1 июль_2 август_1 август_2

Число особей на 1 гектар

2 А

0.1

100

1000

май_2

июнь

июнь_2

июл

вгуст_1

ав

ус

Чсило особей на 1 гектар

Leptidea morsei Fent. in Butler Neptis rivularis Scp.

Aporia crataegi L.

2 Б

Рис. 2. Линейные графики динамики лёта некоторых дневных ба-

бочек в среднегорных березово-еловых лесах Северо-Восточного

Алтая.

А - график построен в обычном масштабе, Б - график построен в

логарифмическом масштабе.

Гистограмма (термин впервые использован Пирсоном в

1895 году) представляет собой графическое отображение вариа-

ционного ряда. На гистограмме по оси абсцисс откладываются

границы классовых интервалов, а по оси ординат – частоты. Затем

для каждого класса рисуется столбец, высота которого пропор-

циональна частоте класса. Основное назначение гистограмм, кро-

ме иллюстративной функции, - выявление соответствия частот

полученного в ходе исследования выборки вариационного ряда

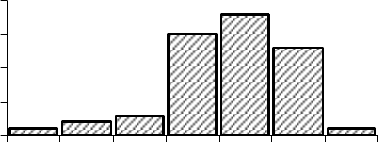
нормальному распределению (см. главу III). На рисунке 3 приве-

дена гистограмма вариационного ряда, построенного по промерам

53 особей большого трубконоса (табл. 3).

36 37.1 38.239.340.4 41.542.6

Длина предплечья,

мм

Частота

Рис. 3. Гистограмма, иллюстрирующая изменчивость длины пред-

плечья у большого трубконоса на Северном Алтае (n=53).

ГЛАВА III

АНАЛИЗ КОЛИЧЕСТВЕННЫХ ПРИЗНАКОВ

3.1. Средняя величина

Важнейшим статистическим параметром можно считать сред-

нюю величину. Будучи чисто математической функцией, средняя

арифметическая, тем не менее, обладает вполне конкретным и

почти интуитивно понятным содержанием. Неслучайно её исполь-

зуют в самых разнообразных отраслях человеческой деятельно-

сти, иногда даже имея смутное представление о математической

статистике и её законах. Полученная средняя величина, в первую

очередь, отражает наиболее типичные значения признака, что по-

зволяет рассматривать её как параметр, на основании которого

можно судить не только о свойствах отдельной выборки, но и о

генеральной совокупности. В общем виде, среднее значение есть

величина, вокруг которой концентрируются все прочие варианты

совокупности. Различают несколько типов средних (средняя квад-

ратическая, средняя кубическая, средняя геометрическая), однако

практически чаще используют среднюю арифметическую величи-

ну. Она представляет собой отношение суммы значений вариантов

к числу наблюдений.

Математически это можно выразить следующей формулой:

xxxx

++++

...

321

, (3.1.)

где М

– среднее арифметическое признака x (от англ. mean –

среднее), n – число наблюдений, Σ - суммирование значений ва-

риантов (x).

При многочисленных выборках, когда по исходным данным по-

строены вариационные ряды, формула для вычисления средней

арифметической приобретает вид:

, (3.2.)

где f – частота вариант по отдельным классам.

В качестве примера рассчитаем по формуле (3.2.) среднее чис-

ло глазков на 40 клубнях картофеля (см. стр. 14)

7.6

267

11110292847126851041

⋅

Средняя арифметическая обладает рядом свойств, часть из ко-

торых позволяет существенно упростить её вычисление. Так, если

все варианты выборки уменьшить (увеличить) на одно и то же

число, то средняя арифметическая соответственно уменьшится

(увеличится) на то же число. Это свойство позволяет вычислять

среднюю арифметическую не по исходным значениям вариантов, а

по уменьшенным (увеличенным) на одно и то же число. Вернёмся

к выше рассмотренному вариационному ряду длины предплечья