Любанова А.Ш. и др. Моделирование процессов и объектов в металлургии. Практикум

Подождите немного. Документ загружается.

ЛАБОРАТОРНАЯ РАБОТА 5. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ

Краткие теоретические сведения



Моделирование процессов и объектов в металлургии. Лаб. практикум

-61-

Сформулированный принцип и уравнение Беллмана носят общий ха-

рактер и применяются не только в задачах дискретной оптимизации. Метод

динамического программирования широко используется для решения многих

экономических задач, связанных с планированием производственных про-

грамм, оптимальным распределением ресурсов (денежных средств, рабочей

силы, сырья и т.д.). Алгоритмы решения таких задач можно найти, например,

в работах [3

, 6].

Поскольку многие особенности реализации метода динамического

программирования определяются конкретными задачами, не имеет смысла

подробно описывать вычислительный алгоритм в общем случае. Поясним

метод на примере одной из наиболее характерных задач

− задаче о кратчай-

шем маршруте.

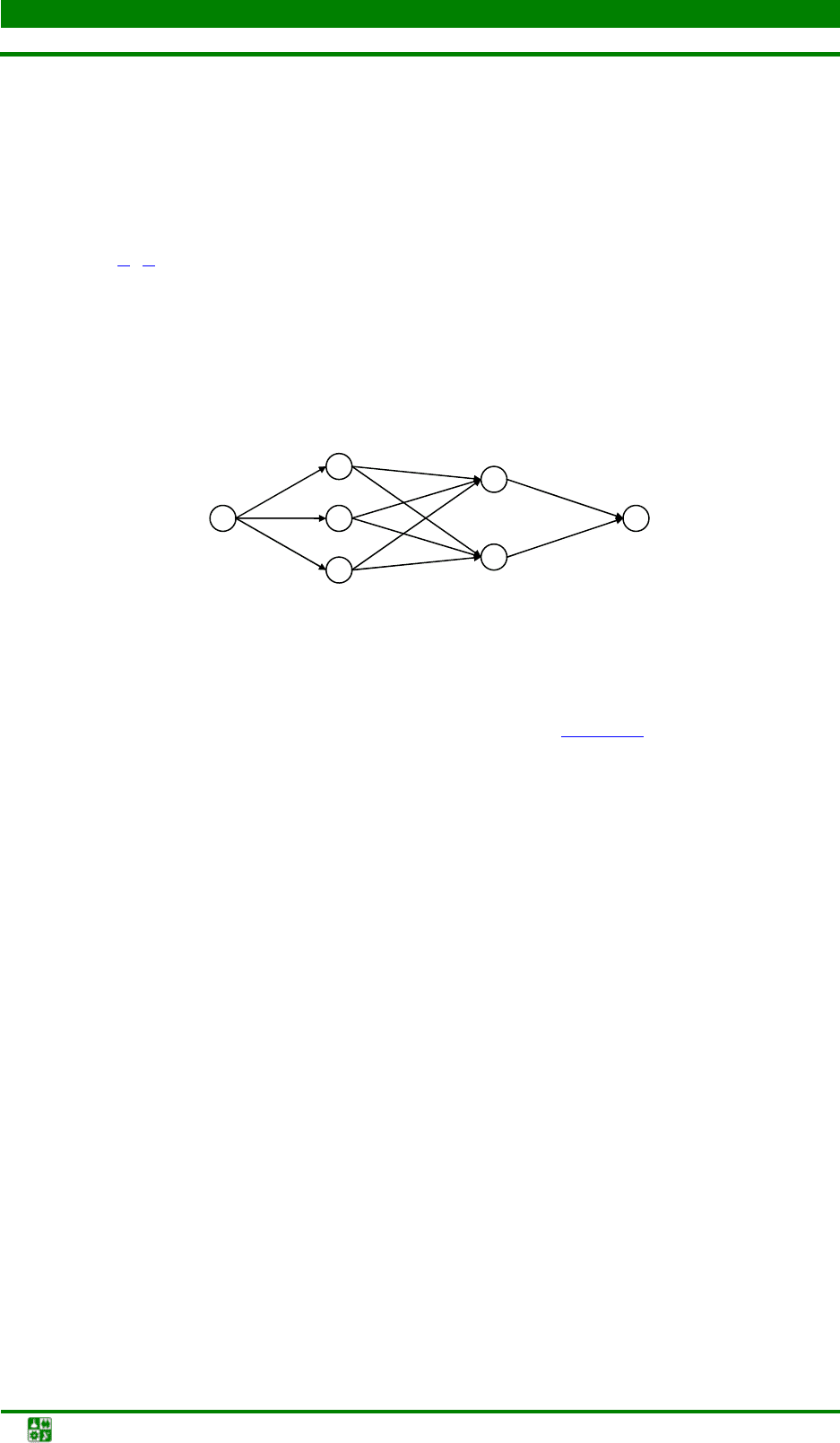
Рис. 5.1. Граф транспортной сети

Пусть требуется перевезти груз из города

А в город В. Сеть дорог, свя-

зывающих эти города, изображена в виде графа на рис. 5.1

. Вершинам графа

поставлены в соответствие города, а дугам – транспортные магистрали.

Стоимость перевозки груза из города

s (s = 1, …, 6) в город j (j = 2, …, 7) про-

ставлена над соответствующими дугами графа. Необходимо найти маршрут,

связывающий города

А и В, для которого суммарные затраты на перевозку

груза были бы наименьшими.

Для решения задачи разобьем все множество вершин (городов) на

подмножества. В первое подмножество включим исходную вершину 1. Во

второе – вершины, в которые входят дуги, выходящие из вершины 1. В третье –

вершины, в которые входят дуги, выходящие из вершин второго подмноже-

ства. Таким образом, продолжая разбиение дальше, получим четыре под-

множеств

а: {1}, {2, 3, 4}, {5, 6}, {7}. Очевидно, что любой маршрут из горо-

да 1 в город 7 содержит ровно три дуги, каждая из которых связывает верши-

ны, принадлежащие соответствующим подмножествам. Следовательно, про-

цесс решения задачи (нахождения оптимального маршрута) разбивается на

три этапа. На первом этапе принимается решение о том, через какой город,

принадлежащий второму подмножеству, везти груз из города 1. На втором

этапе нео

бходимо определить, через какой город третьего подмножества вез-

ти груз из некоторого города, принадлежащего второму подмножеству. На

последнем (третьем) этапе формируется оптимальный маршрут.

Перенумеруем этапы от конечной вершины графа к начальной и вве-

дем обозначения:

n – номер шага (n = 1, 2, 3); f

(s) – минимальные затраты на

ЛАБОРАТОРНАЯ РАБОТА 5. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ

Краткие теоретические сведения



Моделирование процессов и объектов в металлургии. Лаб. практикум

-62-

перевозку груза от города s до конечного города В, если до конечного города

осталось

n шагов; j

(s) – номер города, через который надо ехать из города s,

чтобы затраты были минимальными

(s); c

s,j

– стоимость перевозки груза из

города

s в город j.

Здесь все обозначения несут важную смысловую нагрузку:

f – это це-

левая функция,

s – состояние системы (номер города), индекс n – динамическая

информация о том, что из города

s до конечного города осталось n шагов.

Предположим, что груз доставлен в город 7, следовательно, число ос-

тавшихся шагов равно нулю (

n = 0) и f

(s) = f

(7) = 0, так как из города 7 груз

вести не надо.

Рассмотрим последний шаг (

n = 1) и вычислим для него значение

функции. Очевидно, что в город 7 груз может быть доставлен из города 5 или

из города 6. Вычислим затраты на перевозку для этих состояний:

(

)

(

)

(

)

15,70 1

5 7 5 0 5, 5, 5 7;=+ =+= = =fcf s j

(

)

(

)

(

)

16,70 1

67303,3,67.=+ =+= = =fcf sj

Чтобы произвести расчет для

n = 2, выдвинем гипотезы о месте нахо-

ждения груза: 1-я гипотеза – груз находится в городе 2; 2-я гипотеза – груз

находится в городе 3; 3-я гипотеза – груз находится в городе 4.

Из города 2 в город 7 можно перевезти груз или через город 5, или

через город 6. Поэтому оптимальный маршрут из города 2 найдем по выра-

жению

(

)

(

)

(

)

[

]

22,512,61

2 min 5 , 6 min 3+5, 4+3 7.

⎡⎤

++= =

⎣⎦

fcfcf

Здесь

s = 2 и j

(2) = 6, т. е. условно-оптимальный маршрут проходит

через город 6. Аналогично для

s = 3 и s = 4:

(

)

(

)

(

)

(

)

23,513,61 2

3min 5, 6 6, 35;

⎡⎤

=+ += =

⎣⎦

fcfcf j

(

)

(

)

(

)

(

)

24,514,61 2

4min 5, 6 9, 45.

⎡⎤

=+ += =

⎣⎦

fcfcf j

Вычисления для третьего шага (

n = 3) показывают, что

(

)

(

)

(

)

(

)

3 1,2 2 1,3 2 1,4 2

1min 2, 3, 4 11,

⎡⎤

=+ + +=

⎣⎦

fcfcfcf

(1) = 2, т.е. минимальные затраты на перевозку груза f

(1) = 11 и оптималь-

ный маршрут проходит через город 2. Далее из вычислений

(2) следует, что

оптимальный маршрут проходит через город 6, так как

(2) = 6. Наконец, из

ЛАБОРАТОРНАЯ РАБОТА 5. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ

Краткие теоретические сведения



Моделирование процессов и объектов в металлургии. Лаб. практикум

-63-

города 6 груз доставляется в конечный город 7 (место назначения). Таким

образом, мы определили оптимальный маршрут

х* = (1–2–6–7), затраты на

перевозку груза по которому составляют

(1) = 4 + 4 + 3 = 11.

Следует отметить, что метод динамического программирования при-

меним только для нахождения кратчайшего пути на связных графах, где лю-

бой маршрут состоит из одного и того же числа дуг, как, например, на рас-

смотренном графе. Для графов более общей структуры используются соот-

ветствующие алгоритмы теории графов [6

1. Изучить основные принципы динамического программирования.

Изучить порядок эксплуатации программных средств.

Получить задание и разрешение преподавателя на выполнение ра-

боты, ответив на его вопросы по исходным данным и порядку работы на

машине.

Ввести данные в ЭВМ и получить решение задачи.

Оформить отчет, в который включить: краткую формулировку цели

и содержания работы, основные положения теории динамического програм-

мирования, вариант задания, результаты расчета на ЭВМ, анализ результатов

и выводы.

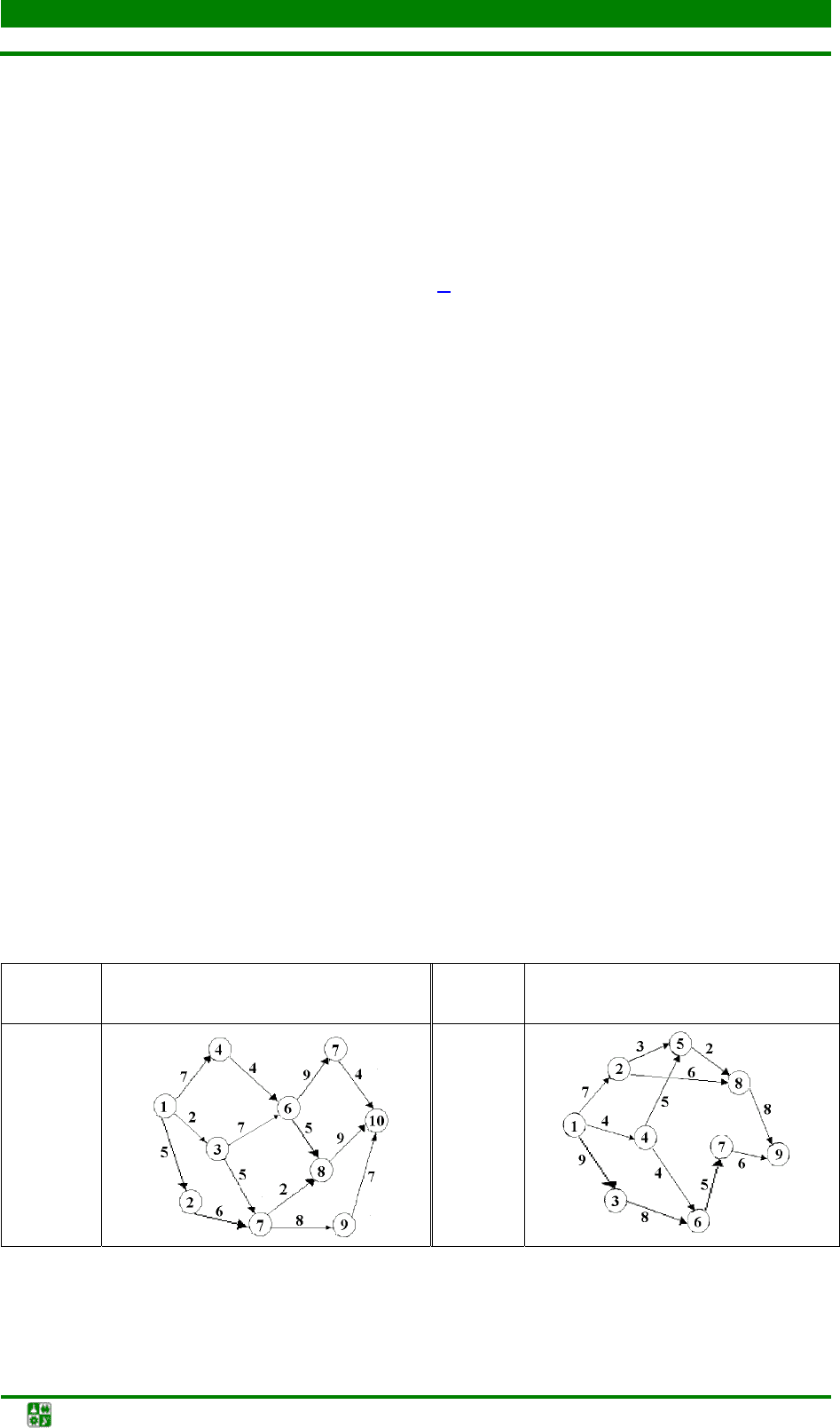
Найти кротчайший путь из первой вершины в последнюю по счету в

заданном графе:

Номер

варианта

Граф

Номер

варианта

Граф

1 2

ЛАБОРАТОРНАЯ РАБОТА 5. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ

Задание



Моделирование процессов и объектов в металлургии. Лаб. практикум

-64-

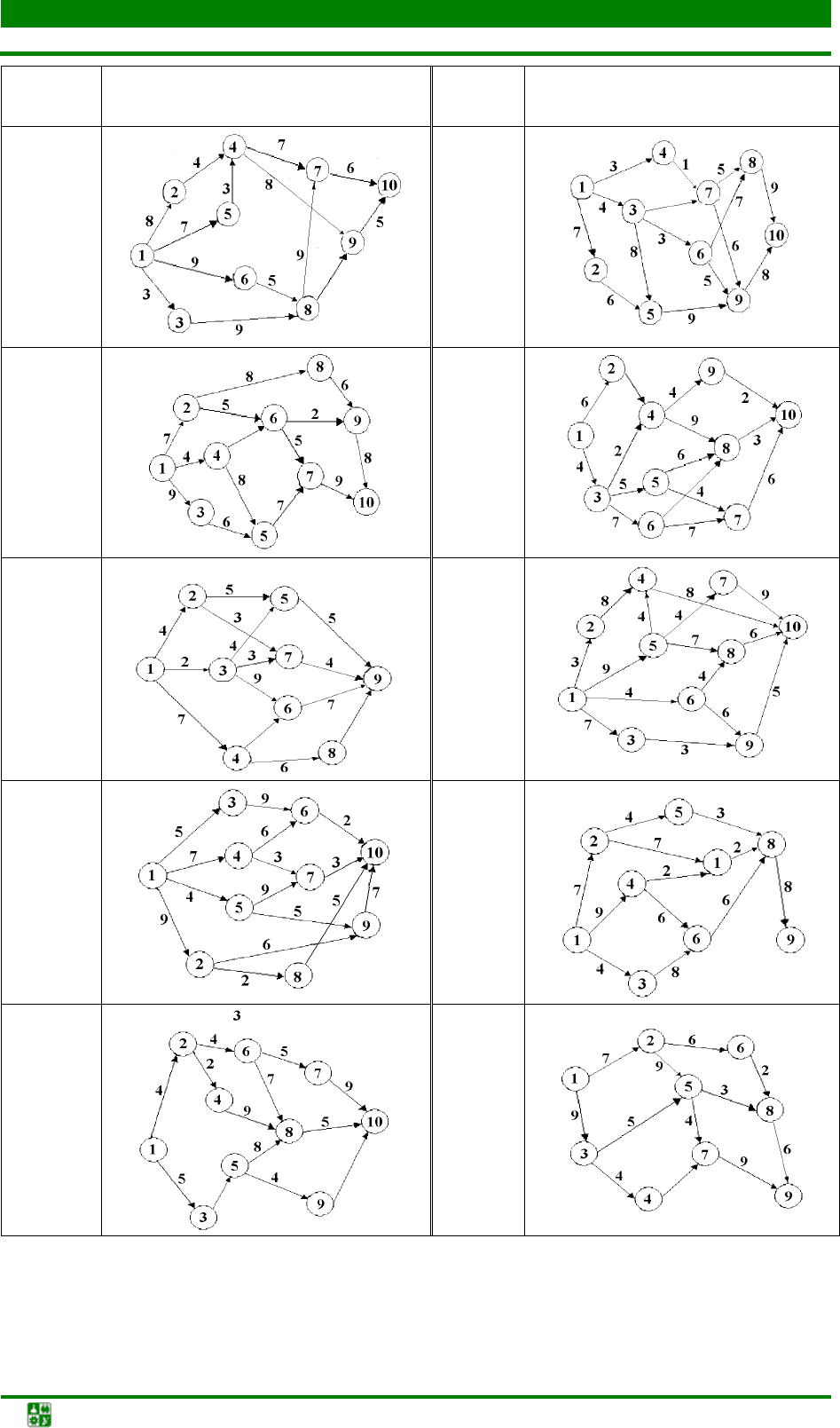
Номер

варианта

Граф

Номер

варианта

Граф

3 4

5 6

7 8

11 12

ЛАБОРАТОРНАЯ РАБОТА 5. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ

Задание



Моделирование процессов и объектов в металлургии. Лаб. практикум

-65-

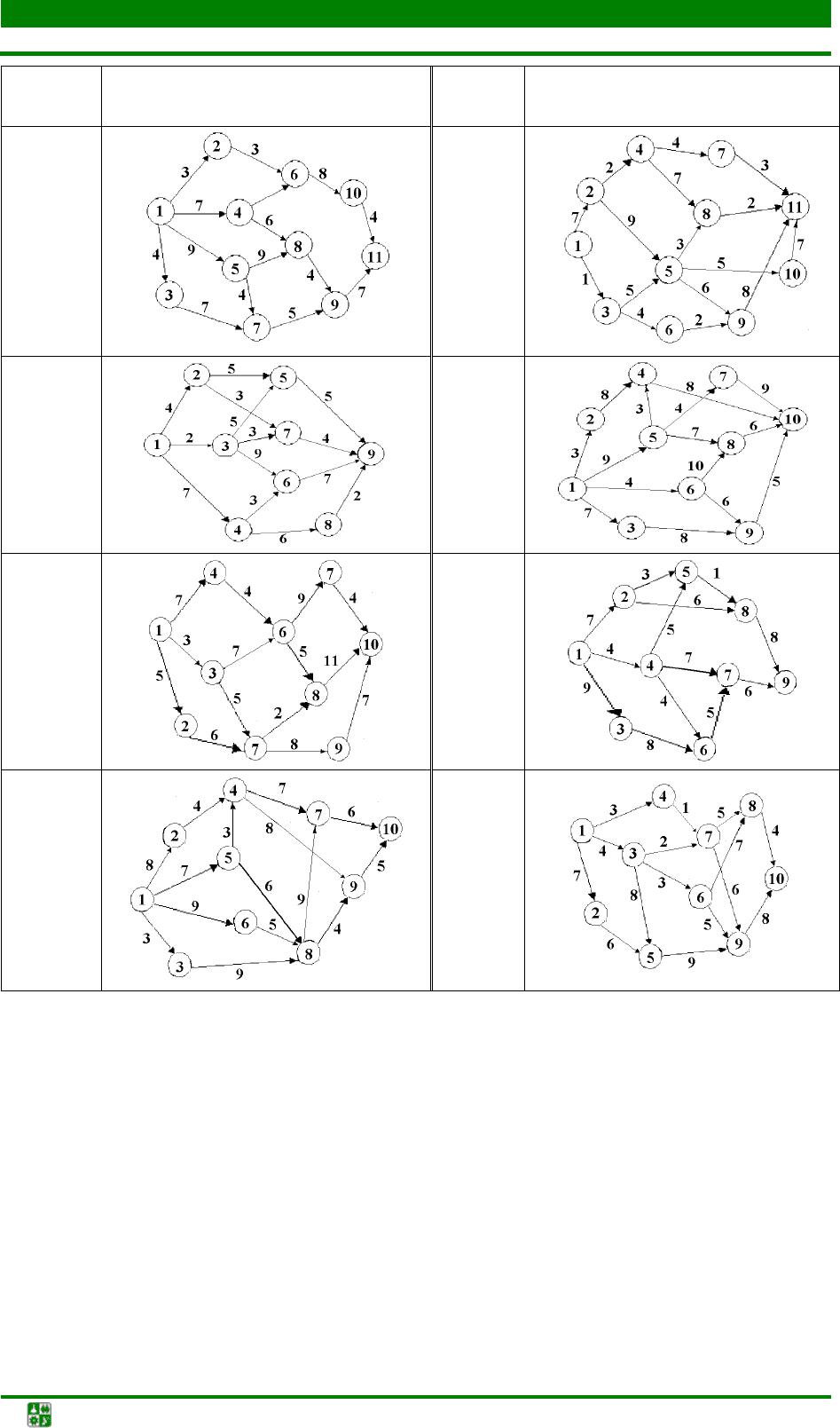
Номер

варианта

Граф

Номер

варианта

Граф

15 16

17 18

19 20

1. Для каких оптимизационных задач применяется метод динамиче-

ского программирования?

В чем заключается суть метода динамического программирования?

Сформулируйте принцип оптимальности Беллмана.

Что является целевой функцией в задаче о кратчайшем маршруте?

5. Какой параметр определяет состояние системы на каждом шаге?



Моделирование процессов и объектов в металлургии. Лаб. практикум

-66-

Установить соответствие между объектом, представленным некоторой

совокупностью экспериментальных данных о его свойствах, и одним из описа-

ний из заданного множества описаний (моделей) объекта.

Под идентификацией объектов понимается построение оптимальных

в некотором смысле математических моделей по реализации их входных и

выходных параметров.

Задача идентификации заключается в количественной оценке степени

идентичности модели реальному объекту.

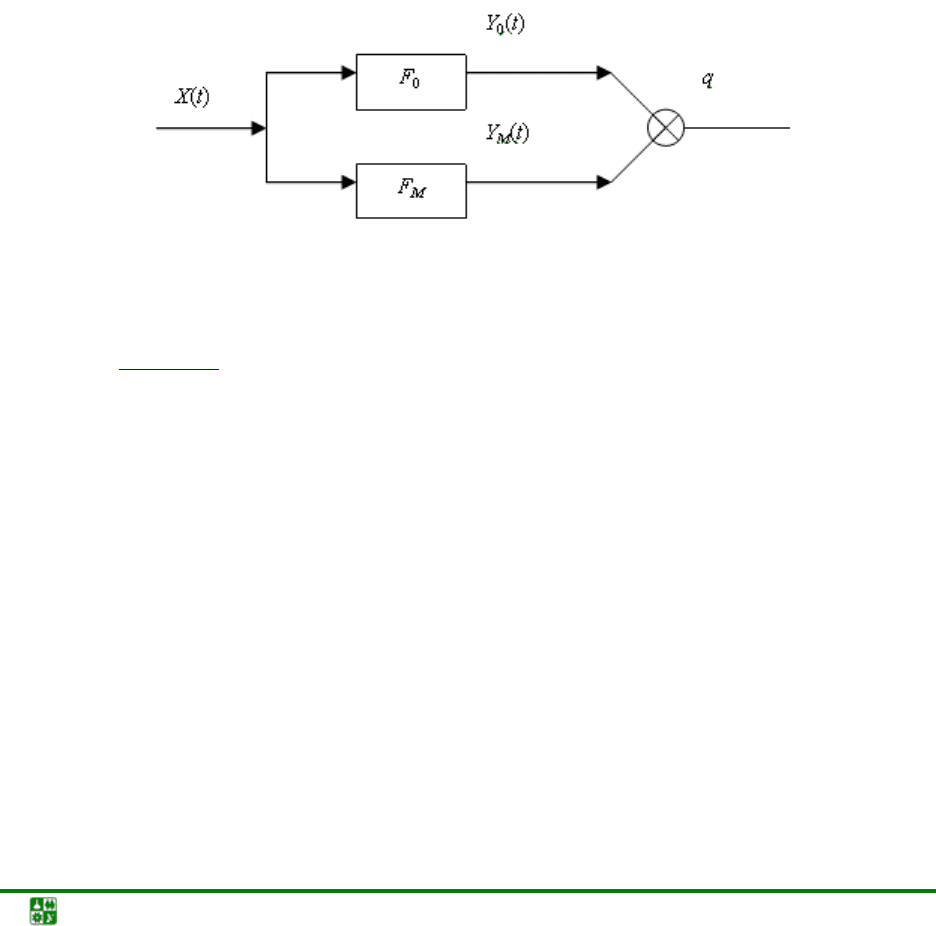
Рис. 6.1. Структурная схема процесса идентификации

Оценка делается на основе сравнения истинной характеристики объ-

екта

(рис. 6.1), представленной его выходными параметрами Y

(t), и

оценки

этой характеристики, описываемой выходными переменными Y

математической модели, зависящими от входных данных

Х(t). Критерием

идентичности модели является минимум её ошибки

q, вычисляемой чаще

всего по формуле

0ì

(() ()).

=−

∑

qYtYt

Идентификация может быть

адаптивной (подстраиваемой, или обу-

чаемой) и

неадаптивной (неподстраиваемой). При неадаптивной идентифи-

кации выбираются или рассчитываются коэффициенты модели и в дальней-

шем эти коэффициенты не изменяются.

ЛАБОРАТОРНАЯ РАБОТА 6. ИДЕНТИФИКАЦИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ

Краткие теоретические сведения



Моделирование процессов и объектов в металлургии. Лаб. практикум

-67-

Основным свойством адаптивной идентификации является то, что ко-

эффициенты математической модели по мере необходимости изменяются

или подстраиваются.

В зависимости от априорной (исходной) информации об объекте раз-

личают

структурную и параметрическую идентификацию.

Предметом структурной идентификации является определение вида

функции

теор

, связывающей входные переменные Х. Структурная идентифи-

кация включает в себя: 1) постановку задачи; 2) выбор структуры модели и её

математическое описание; 3) исследование модели. На этапе параметриче-

ской идентификации выполняется экспериментальная проверка модели.

Существующие представления об объекте и его выходные параметры

отражаются в виде определенной функции

Y(Х, b) с неизвестными коэффици-

ентами

B = (b

, …, b

). Процедуры же конкретной реализации функции осно-

вываются на функциональном представлении зависимости выходных пере-

менных модели от входных.

Задача идентификации ставится как задача оптимизации

(B) → min, Y ∈ F

где

Q – мера расхождения между выходными экспериментальными парамет-

рами объекта и выходными переменными выбираемой модели (суммарная

невязка). При структурной идентификации

) – класс операторов, среди

которых выбирается структура модели. При параметрической идентифика-

ции

) – допустимая область в пространстве внутренних параметров Y мо-

дели.

Выбор структуры модели и её математическое описание

осуществля-

ются с учетом характера протекания процесса как объекта моделирования.

Непрерывные металлургические процессы происходят при непрерыв-

ной загрузке материалов и выгрузке продуктов переработки (процесс спека-

ния глинозема, электролиз алюминия, плавка сульфидных руд в печах и т.д.).

Полунепрерывные процессы характеризуются непрерывной загрузкой

материала в течение какого-то времени проведения процесса, отключением

агрегата и выпуском продуктов переработки.

Периодические (циклические) процессы связаны с разовой загрузкой

материалов, проведением технологического процесса и выгрузкой готовых

продуктов переработки (выращивание монокристаллов кремния, обжиг ке-

рамики).

Для определения структуры модели необходимо решить две задачи.

1. Выделение входных и выходных параметров объекта по степени их

влияния на конечный целевой показатель. При построении структуры модели

ЛАБОРАТОРНАЯ РАБОТА 6. ИДЕНТИФИКАЦИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ

Краткие теоретические сведения



Моделирование процессов и объектов в металлургии. Лаб. практикум

-68-

в нее целесообразно включать не все входные и управляющие параметры, а

только те, которые оказывают решающее влияние на выходную переменную.

Не следует вводить в модель несущественные параметры, так как это приво-

дит к значительному усложнению модели.

2. Определение характера связи между входными и выходными пара-

метрами, т.е. выбор класса операторов

. По характеру связи математиче-

ские модели делят на линейные и нелинейные.

Линейные модели использу-

ются для описания линейных процессов, т.е. процессов, в которых связь ме-

жду входной и выходной переменными характеризуется линейной зависимо-

стью.

Нелинейные модели применяются для описания нелинейных процессов,

т.е. процессов, в которых связь между входной и выходной переменными ха-

рактеризуется нелинейной зависимостью.

Исследование модели на адекватность объекту осуществляется с по-

мощью анализа остатков модели (см. лаб. работу 1

Целью параметрической идентификации является уточнение (под-

стройка) внутренних параметров, т.е. коэффициентов математической моде-

ли в тех случаях, когда с помощью структурной идентификации не удается

достичь необходимой адекватности модели реальному объекту.

Для стохастических объектов предполагается, что свойства случайной

составляющей не зависят от входной переменной

Х, т.е. полностью оценива-

ются определенной плотностью вероятности, в качестве которой часто при-

нимают плотность нормального закона распределения.

После структурной идентификации, при которой неизвестная функция

объекта

Y(Х) представляется в виде известной функции с неизвестными па-

раметрами

Y(Х, b), осуществляется экспериментальная проверка модели. Для

уточнения коэффициентов решается следующая оптимизационная задача.

Образуются невязки выходных параметров модели и объекта на каждом

i-м измерении, называемые локальными невязками:

(b) = Y

– Y(x, b) i = 1, ..., n.

Оцениваемые параметры выбираются таким образом, чтобы все эти

невязки были минимальны по модулю, т.е. решается задача минимизации

функций:

(b) → min, i = 1, …, n,

где вектор b может принимать любые значения. Эта задача является много-

критериальной и может быть заменена однокритериальной задачей миними-

зации суммарной невязки

Q(b) → min,

ЛАБОРАТОРНАЯ РАБОТА 6. ИДЕНТИФИКАЦИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ

Краткие теоретические сведения



Моделирование процессов и объектов в металлургии. Лаб. практикум

-69-

на всем пространстве векторов b .

На практике используют какой-либо из следующих критериев:

Критерий Расчетная формула

Модульный

() ()

∑

Qb q b

Квадратичный

() ()

∑

Qb q b

Показательный

() ()

∑

Qb q b

Минимаксный

(

)()

1,...,

max

Qb q b

Взвешенный

() ()

⎡

⎤

=λ

⎢

⎥

⎣

⎦

∑

Qb q b ,

где λ

> 0 – заданные веса

Задача идентификации теперь сводится к оценке суммарной невязки,

которая служит основным критерием, по нему проводится идентификация

модели.

При этом результат идентификации будет зависеть от выбора крите-

рия, так как различные критерии могут давать минимумы, отличающиеся

друг от друга по значению и положению точек минимума.

Если относительная квадратичная невязка

() ()

⎥

⎦

⎤

⎢

⎣

⎡

∑∑

YbqbQ

не превышает 5 % от суммы квадратов экспериментальных

выходного па-

раметра объекта, то модель считается адекватной.

Открыть файл, созданный при выполнении лабораторной работы 1.

Скопировать таблицу (см. рис. 1.8

) на другой лист рабочей книги текущего

файла, размер листа установить альбомный. Удалить данные столбца D.

Выбрать критерий параметрической идентификации. Для нахожде-

ния модульного критерия в ячейку D3 записать формулу =ABS(B3-C3) и ско-

пировать ее на весь столбец D. Для определения квадратичного критерия в

ячейку E3 записать формулу =СТЕПЕНЬ(B3-C3;2) и скопировать ее на весь

столбец E.

ЛАБОРАТОРНАЯ РАБОТА 6. ИДЕНТИФИКАЦИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ

Порядок выполнения работы



Моделирование процессов и объектов в металлургии. Лаб. практикум

-70-

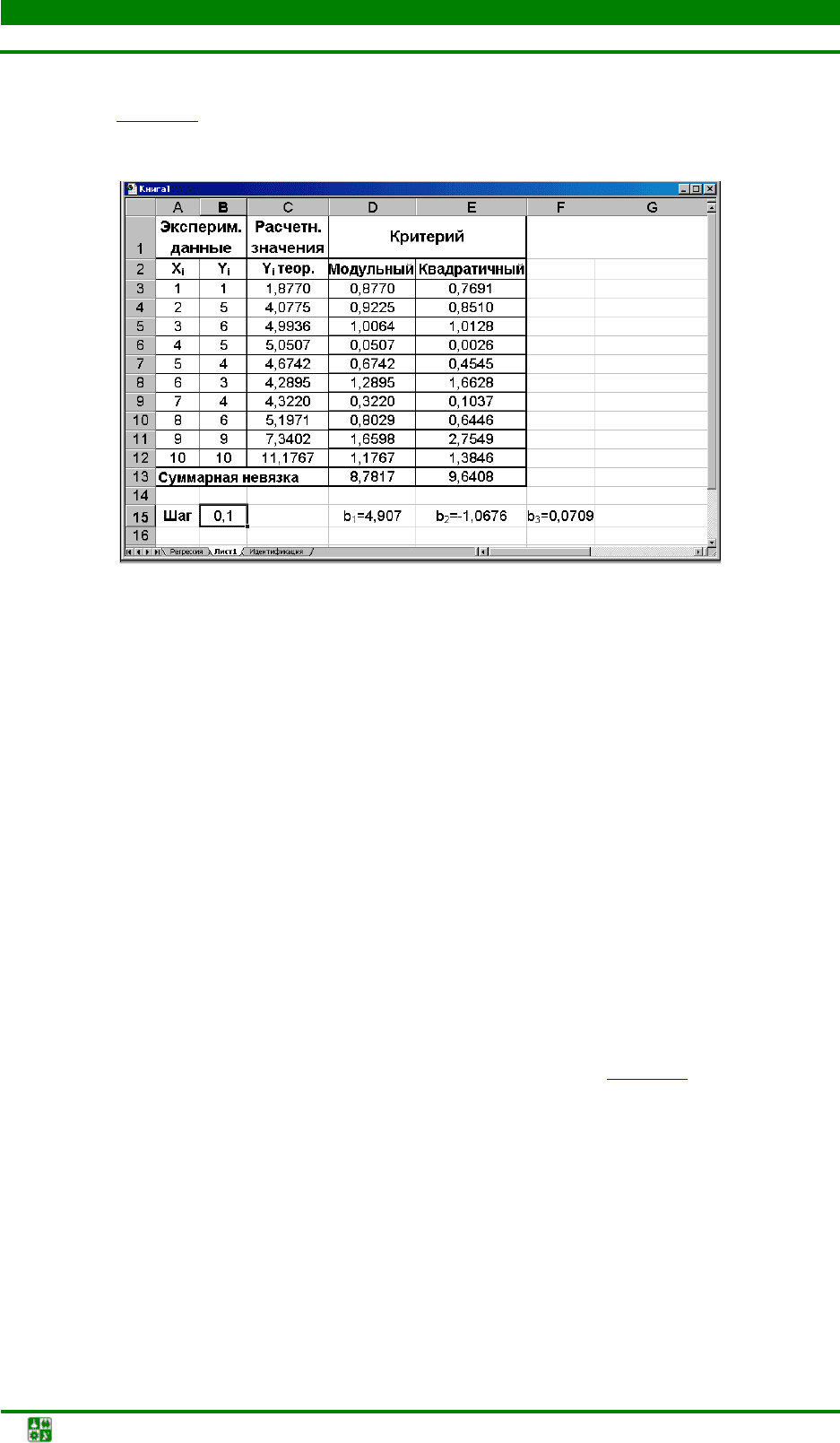
Найти суммарную ошибку модели (невязку) с помощью функции

СУММ() (рис. 6.2). По минимальному значению суммарной невязки выбрать

критерий.

Рис. 6.2. Выбор критерия по минимальной

суммарной невязке

Уточнить коэффициенты выбранной модели. Уточнение коэффици-

ентов производится по основному критерию идентификации модели – сум-

марной невязке, которая при оптимальных значениях коэффициентов должна

быть минимальной. Для того чтобы установить, как влияет каждый из коэф-

фициентов в отдельности на выходной параметр

Y, необходимо менять зна-

чение одного из коэффициентов с определенным шагом, оставляя при этом

другие коэффициенты постоянными. Уточнение коэффициентов выполнить

по следующему алгоритму.

3.1. Задать начальное значение шага 0,1 в ячейке B15 и рядом в сво-

бодных ячейках записать все значения коэффициентов, кроме свободного ко-

эффициента

3.2. В ячейки F3 и I3 записать значение коэффициента

. Скопировать

на весь столбец F увеличение значения свободного коэффициента, а на стол-

бец I скопировать уменьшение значения

с шагом 0,1 (рис. 6.3).

3.3. В ячейки G3 и J3 поместить уравнение регрессии, только вместо

коэффициента

(с учетом знака b

) записать, соответственно, имя ячейки F3

=0,0709*A3^3-1,0676*A3^2+4,907*A3+F3

и скопировать формулу на весь столбец G. Затем в ячейку J3 записать формулу

=0,0709*C3^3-1,0676*C3^2+4,907*C3+I3