Любанова А.Ш. и др. Моделирование процессов и объектов в металлургии. Практикум

ЛАБ. Р. 3. ПРИМЕНЕНИЕ МЕТОДОВ ЛИНЕЙНОГО ПРОГР-Я ДЛЯ МОДЕЛИРОВАНИЯ И РЕШ-Я ПРОИЗВОДСТВЕННЫХ З

А

Д

АЧ

Задания



Моделирование процессов и объектов в металлургии. Лаб. практикум

-51-

Продолжение табл. 3.1

18 Min

21

2xx

−

63

5

12

63

21

≥−

≤+

≤+−

≥+

xx

19 Max

21

2 xx

+

2

1010

21

≥+

xx

20 Min

12

2

x

−

12

123

124

28

8

216

15 100

xx

xxx

+≤

−≥

−+ + =

+−=

Задание 2

На предприятии имеется возможность выпускать

n видов продукции

(1,)

j

П

jn= . При ее изготовлении используются ресурсы

123

,,PPP. Размеры

допустимых затрат ресурсов ограничены, соответственно, величинами

123

,,bbb. Расход ресурса i-го (1,3)i = вида на единицу продукции j-го вида

составляет

ij

a ед. Цена единицы продукции i-го вида равна

j

c ден. ед. Требу-

ется:

1) симплекс-методом найти план выпуска продукции по видам с уче-

том имеющихся ограниченых ресурсов, который обеспечивал бы предпри-

ятию максимальный доход. Дать содержательный ответ, вскрыв экономиче-

ский смысл всех переменных, участвующих в решении задачи;

2) сформулировать в экономических терминах двойственную задачу и

составить ее математическую модель;

3) используя решение исходной задачи и соответствие между двойст-

венными переменными, найти компоненты оптимального плана двойствен-

ной задачи – двойственные оценки

*

(1,3)

i

yi= .

Все необходимые числовые данные приведены в табл. 3.2, табл. 3.3.

Таблица 3.2

Параметр

Номер варианта

1 2 3

4 5

6 7 8 9 10

n

4 3 4 3 3 3 3 4 3 3

b

1

20 150 280 1 200 600 24 500 100 360 180

b

2

37 180 80 150 30 10 550 260 192 210

b

3

30 120 250 3 000 144 6 200 370 180 244

ЛАБ. Р. 3. ПРИМЕНЕНИЕ МЕТОДОВ ЛИНЕЙНОГО ПРОГР-Я ДЛЯ МОДЕЛИРОВАНИЯ И РЕШ-Я ПРОИЗВОДСТВЕННЫХ З

А

Д

АЧ

Задания



Моделирование процессов и объектов в металлургии. Лаб. практикум

-52-

Продолжение табл. 3.2

Пара-

метр

Номер варианта

1 2 3 4 5 6 7 8 9 10

a

11

2 2 2 15 10 5 2 2,5 18 4

a

12

2 3 1 20 20 7 1 2,5 15 2

a

13

3 4 1 25 23 4 0 2 12 1

a

14

0 – 1 – – – – 1.5 – –

a

21

3 1 1 2 1 5 0 4 6 3

a

22

1 4 0 3 1 2 2 10 4 1

a

23

1 5 1 2.5 1 1 1 4 8 3

a

24

2 – 1 – – – – 6 – –

a

31

0 3 1 35 5 2 0 8 5 1

a

32

1 4 2 60 6 1 1 7 3 2

a

33

1 2 1 60 6 1 0 4 3 5

a

34

4 – 0 – – – – 10 – –

c

1

11 8 4 300 35 18 3 40 9 10

c

2

6 7 3 250 60 12 4 50 10 14

c

3

9 6 6 450 63 8 1 100 16 12

c

4

6 – 7 – – – – 80 – –

Таблица 3.3

Параметр

Номер варианта

11 12 13 14 15

16

17 18 19 20

n

4 5 3 3 3 4 5 4 4 3

b

1

2 3 400 6 000 12 1 000 3 4 24 12

b

2

2 2 250 5 000 25 500 5 3 12 27

b

3

2 2 200 9 000 18 1 200 4 3 35 6

a

11

1 1

1

/

6

1 6 1 1 1 1 2

a

12

1 1

3

/

7

1 4 2 2 3 2 1

a

13

0 1

1

/

4

1 3 3 3 0 4 6

a

14

2 2 – – – 1 6 1 8 –

a

15

– 2 – – – – 2 – – –

a

21

0 0

1

/

4

1

/

2

5 2 2 2 3 3

a

22

1 1

1

/

7

1 3 1 3 1 5 3

a

23

1 1

1

/

4

5 2 0 1 0 1 9

a

24

0 1 – – – 0 6 0 0 –

a

25

– 2 – – – 0 0 – – –

a

31

1 1

1

/

6

1

/

2

4 0 3 0 6 2

a

32

0 1

1

/

7

1

/

2

5 1 1 1 0 1

a

33

1 0

3

/

8

20 4 4 2 4 3 2

a

34

0 2 – – – 1 6 1 1 –

a

35

– 1 – – – – 4 – – –

c

1

3 5 120 80 1 2 3 2 0,4 14

c

2

7 2 100 100 2 40 4 4 0,2 6

c

3

4 8 150 300 3 10 1 1 0,5 22

c

4

2 3 – – – 15 3 1 0,8 –

c

5

– 6 – – – – 2 – – –

ЛАБ. Р. 3. ПРИМЕНЕНИЕ МЕТОДОВ ЛИНЕЙНОГО ПРОГР-Я ДЛЯ МОДЕЛИРОВАНИЯ И РЕШ-Я ПРОИЗВОДСТВЕННЫХ З

А

Д

АЧ



Моделирование процессов и объектов в металлургии. Лаб. практикум

-53-

К

о

н

т

р

о

л

ь

н

ы

е

в

о

п

р

о

с

ы

и

з

а

д

а

н

и

я

1. Сформулируйте общую задачу линейного программирования.

2.

Чем отличается общая задача линейного программирования от ка-

нонической?

3.

Всегда ли общую задачу линейного программирования можно при-

вести к канонической форме? Опишите метод приведения общей задачи к

каноническому виду.

4.

Чем отличается выпуклый многогранник от выпуклого многогран-

ного множества?

5.

Дайте определение угловой точки выпуклого многогранного мно-

жества?

6.

Перечислите свойства задач линейного программирования.

7.

Сформулируйте основную теорему линейного программирования.

8.

В чем заключается первая геометрическая интерпретация задачи

линейного программирования?

9.

В чем состоит идея геометрического метода решения задачи ли-

нейного программирования? Для каких задач он применяется?

10.

В чем заключается вторая геометрическая интерпретация задачи

линейного программирования?

11.

Дайте определения следующих понятий: опорная точка допусти-

мого множества (базисное решение), базис опорной точки, базисные пере-

менные.

12.

Какая опорная точка называется вырожденной (невырожденной)?

13.

Какая задача ЛП называется вырожденной (невырожденной)?

14.

В чем состоит различие между симплекс-методом и методом пол-

ного перебора опорных точек допустимого множества?

15.

Как с помощью симплекс-метода определить, что задача ЛП не

имеет решения?

16.

Что такое разрешающий элемент и разрешающее уравнение? Для

чего они используются?



Моделирование процессов и объектов в металлургии. Лаб. практикум

-54-

Л

А

Б

О

Р

А

Т

О

Р

Н

А

Я

Р

А

Б

О

Т

А

4

Т

Р

А

Н

С

П

О

Р

Т

Н

А

Я

З

А

Д

А

Ч

А

Ц

е

л

ь

р

а

б

о

т

ы

Ознакомиться со структурой транспортных задач, методами их реше-

ния и анализа результатов; приобрести навыки в проведении вычислительно-

го эксперимента на ЭВМ.

К

р

а

т

к

и

е

т

е

о

р

е

т

и

ч

е

с

к

и

е

с

в

е

д

е

н

и

я

Одним из наиболее важных частных случаев общей задачи линейного

программирования является так называемая

транспортная задача. Содер-

жательно она формулируется следующим образом.

Пусть в пунктах

А

1

, А

2

, …, А

m

изготавливается некоторый однородный

продукт, причем объем производства этого продукта в пункте

A

i

составляет

a

i

ед., i = 1, …, m. Произведенный продукт должен быть доставлен в пункты

потребления

В

1

, В

2

, …, В

n

, причем объем потребления в пункте B

j

составляет

b

j

ед. продукта. Предполагается, что транспортировка готовой продукции

возможна из любого пункта производства в любой пункт потребления и

транспортные издержки, приходящиеся на перевозку единицы продукта из

пункта

А

i

в пункт В

j

, составляют c

ij

ден. ед. Задача состоит в организации та-

кого плана перевозок, при котором суммарные транспортные издержки были

бы минимальными.

Обозначим через

ij

x количество продукта, перевозимого c i-го пред-

приятия к

j-му потребителю. План перевозки груза в данной транспортной

сети представляет собой массив элементов размерности

m × n:

x = (x

1,1

, …, x

1,n

, x

2,1

, …, x

2,n

, …, x

m,1

, …, x

m,n

).

Если реальная перевозка между пунктами

i и j отсутствует, то пола-

гают

x

i,j

= 0.

Ограничения на возможные значения

x ∈ R

mn

включают в себя:

ограничения на удовлетворение потребностей во всех пунктах по-

требления:

,

1

,1,...,;

=

≥=

∑

m

ij j

i

x

bj n

(4.1)

ЛАБОРАТОРНАЯ РАБОТА 4. ТРАНСПОРТНАЯ ЗАДАЧА

Краткие теоретические сведения



Моделирование процессов и объектов в металлургии. Лаб. практикум

-55-

ограничения на возможности вывоза запасов из всех пунктов произ-

водства:

,

1

,1,,;

=

≤=

∑

…

n

ij i

j

x

ai m

(4.2)

условия неотрицательности компонент плана:

x

i,j

≥ 0, i = 1, …, m, j = 1, …, n. (4.3)

Математически транспортная задача ставится следующим образом:

определить точку минимума функции суммарных транспортных издержек

()

∑∑

==

=

m

i

n

j

jiij

xcxf

11

,

при ограничениях (4.1)

, (4.2), (4.3).

Полученная задача является задачей линейного программирования.

Существенная характеристика описываемой задачи – соотношение парамет-

ров

a

i

и b

j

. Если суммарный объем производства равен суммарному объему

потребления, а именно выполняется

условие баланса

∑∑

==

=

m

i

n

j

ji

ba

11

,

(4.4)

то система называется

сбалансированной. При выполнении условия баланса

разумно накладывать такие ограничения на суммарный ввоз и вывоз груза,

при которых полностью вывозится весь груз и не остается неудовлетворен-

ных потребностей, т.е. условия (4.1)

, (4.2) приобретают форму равенства.

При таких ограничениях выполнение равенства (4.4)

становится необходи-

мым и достаточным условием для разрешимости транспортной задачи.

П

о

р

я

д

о

к

в

ы

п

о

л

н

е

н

и

я

р

а

б

о

т

ы

1. Изучить постановку и методы решения транспортных задач.

2.

Изучить порядок эксплуатации программных средств решения за-

дачи ЛП с помощью ЭВМ.

3.

Получить разрешение преподавателя на выполнение работы, отве-

тив на его вопросы по исходным данным и порядку работы на машине.

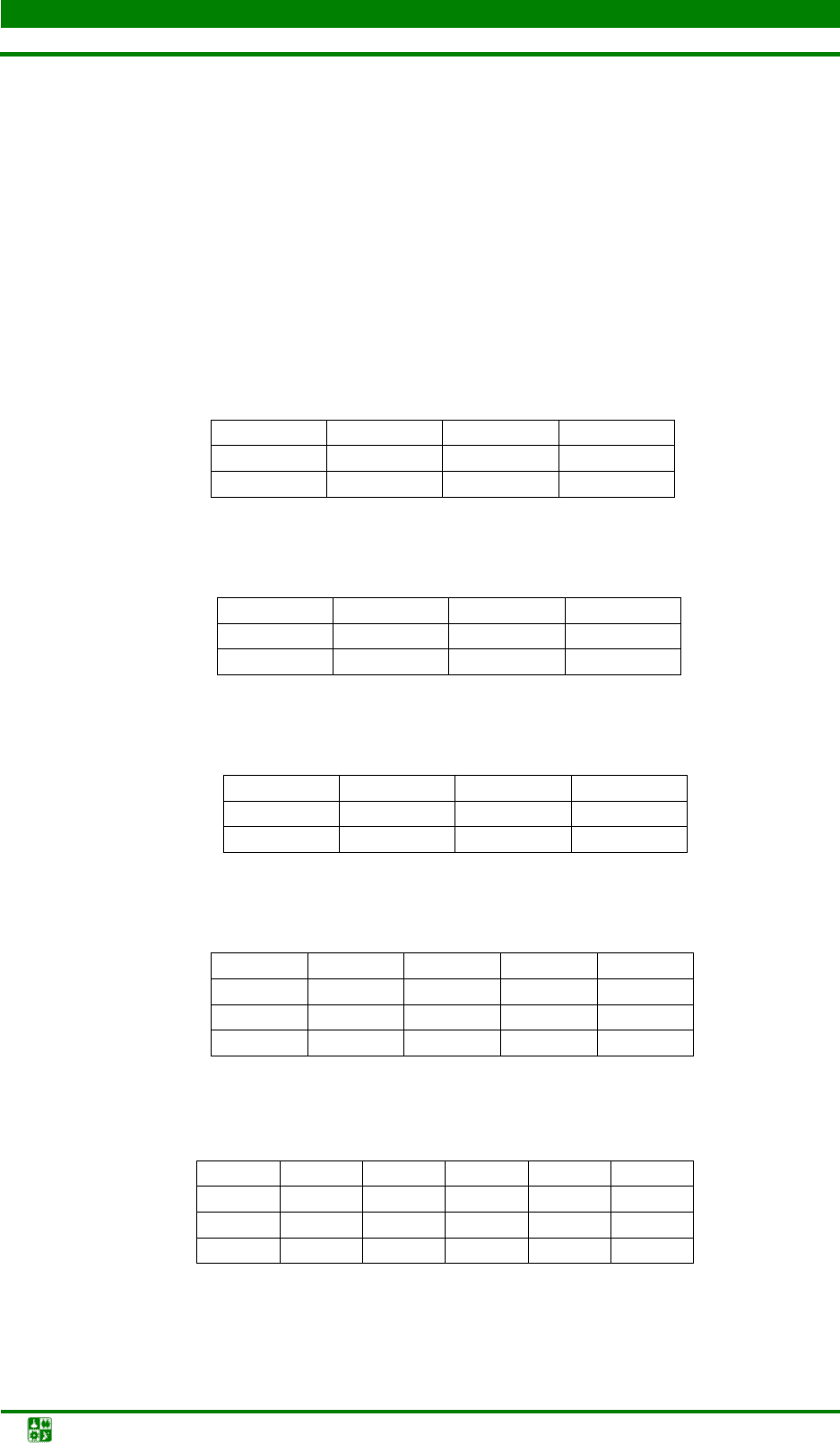
ЛАБОРАТОРНАЯ РАБОТА 4. ТРАНСПОРТНАЯ ЗАДАЧА

Порядок выполнения работы



Моделирование процессов и объектов в металлургии. Лаб. практикум

-56-

4. Ввести данные в ЭВМ в соответствии с вариантом задания и полу-

чить решение задачи.

5.

Оформить отчет, в который включить: титульный лист, краткую

формулировку цели и содержания работы, математическую модель транс-

портной задачи, краткое описание методов решения, задание, результаты

расчета на ЭВМ, анализ результатов.

З

а

д

а

н

и

е

Вариант 1

15 20 20 30

50 13 17 17 14

25 18 16 16 18

25 12 14 19 17

Вариант 2

120 50 190 110

160 7 8 1 2

140 4 5 9 8

170 9 2 3 6

Вариант 3

1 500 2 500 2 700 3 300

6 000 1 4 1 9

3 000 9 2 2 8

3 000 6 1 7 3

Вариант 4

250 1 000 700 650 450

950 12 14 21 19 32

300 4 4 9 5 24

1 350 3 8 14 10 26

450 24 33 36 34 49

Вариант 5

6 4 10 13 7 10

9 2 9 3 10 8 7

14 3 2 6 3 5 2

16 1 8 2 4 1 5

11 4 8 7 6 6 6

ЛАБОРАТОРНАЯ РАБОТА 4. ТРАНСПОРТНАЯ ЗАДАЧА

Задание



Моделирование процессов и объектов в металлургии. Лаб. практикум

-57-

Вариант 6

120 125 130 110 140

145 18 24 23 27 32

125 19 20 14 16 26

220 21 20 17 15 28

135 15 21 22 19 22

Вариант 7

120 60 60 80

180 2 3 4 3

60 5 3 1 2

80 2 1 4 2

Вариант 8

50 30 20

12 15 19 14

15 19 18 16

26 19 18 20

36 15 19 18

Вариант 9

4 9 9 13

8 4 3 3 1

11 3 2 4 8

16 5 4 6 3

Вариант 10

30 30 10 20

50 1 2 4 1

30 2 3 1 5

Вариант 11

110 90 120 80 150

180 7 12 4 6 5

350 1 8 6 5 3

20 6 16 8 7 4

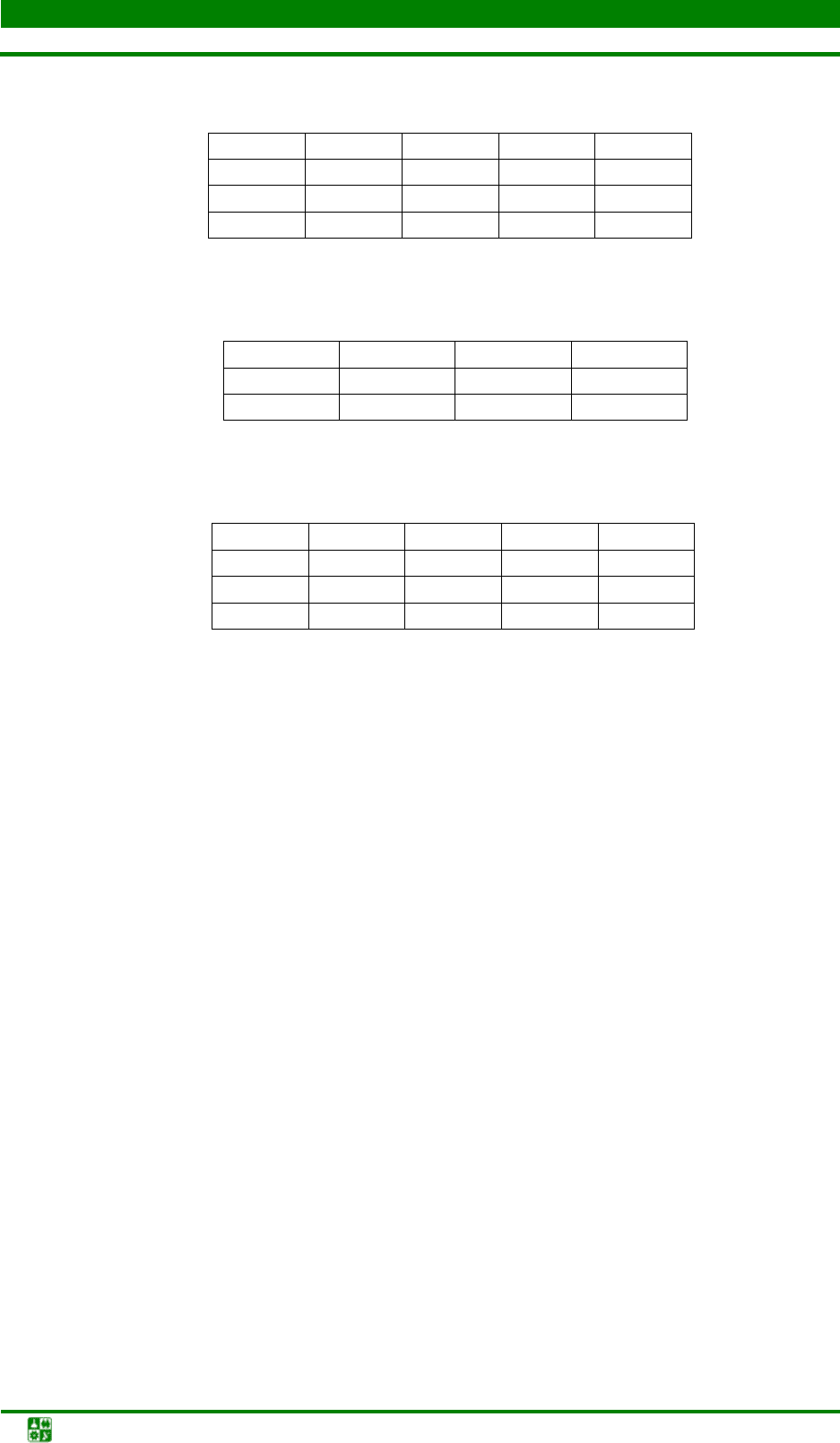
Вариант 12

10 15 20 10 15

20 24 16 8 10 14

30 21 15 7 12 16

20 23 14 7 14 12

ЛАБОРАТОРНАЯ РАБОТА 4. ТРАНСПОРТНАЯ ЗАДАЧА

Задание



Моделирование процессов и объектов в металлургии. Лаб. практикум

-58-

Вариант 13

250 1 000 700 650 450

950 12 14 21 19 32

300 4 4 9 5 24

350 3 8 14 10 26

450 24 33 36 34 49

Вариант 14

1 500 2 500 2 700 3 300

6 000 1 4 1 9

3 000 9 2 2 8

3 000 6 1 7 3

Вариант 15

120 125 130 110 140

145 18 24 23 27 32

125 19 20 14 16 26

220 21 20 17 15 28

135 15 21 22 19 22

К

о

н

т

р

о

л

ь

н

ы

е

в

о

п

р

о

с

ы

и

з

а

д

а

н

и

я

1.

Дайте содержательную формулировку транспортной задачи.

2.

Какие ограничения задают допустимое множетво транспортной за-

дачи?

3.

Каков экономический смысл решения транспортной задачи?

4.

Можно ли решать транспортную задачу методами линейного про-

граммирования?

5.

Сформулируйте условие баланса. Какова его роль в транспортных

задачах?

6.

Когда транспортна задача называется сбалансированной?



Моделирование процессов и объектов в металлургии. Лаб. практикум

-59-

Л

А

Б

О

Р

А

Т

О

Р

Н

А

Я

Р

А

Б

О

Т

А

5

Д

И

Н

А

М

И

Ч

Е

С

К

О

Е

П

Р

О

Г

Р

А

М

И

Р

О

В

А

Н

И

Е

Ц

е

л

ь

р

а

б

о

т

ы

Изучить теорию и методы решения задач динамического программи-

рования; приобрести навыки решения задач динамического программирова-

ния на ЭВМ.

К

р

а

т

к

и

е

т

е

о

р

е

т

и

ч

е

с

к

и

е

с

в

е

д

е

н

и

я

Динамическое программирование представляет собой математиче-

ский метод для нахождения оптимальных решений многошаговых (много-

этапных) задач оптимизации.

М

н

о

г

о

ш

а

г

о

в

ы

е

п

р

о

ц

е

с

ы

в

д

и

н

а

м

и

ч

е

с

к

и

х

з

а

д

а

ч

а

х

Некоторые задачи математического программирования обладают спе-

цифическими особенностями, которые позволяют свести их решение к рас-

смотрению множества более простых «подзадач». В результате вопрос о гло-

бальной оптимизации целевой функции сводится к поэтапной оптимизации

некоторых промежуточных целевых функций.

Пусть, например, на период времени

Т, состоящий из m лет, планиру-

ется деятельность группы промышленных предприятий. В начале планируе-

мого периода на развитие предприятий выделяются основные средства

Q

0

,

которые необходимо распределить между предприятиями. В процессе функ-

ционирования предприятий выделенные им средства частично расходуются.

Однако каждое из этих предприятий за определенный период времени (хо-

зяйственный год) получает прибыль, зависящую от объема вложенных

средств. В начале каждого года имеющиеся средства могут перераспреде-

ляться между предприятиями. Требуется определить, сколько средств надо

выделить каждом

у предприятию в начале каждого года, чтобы суммарный до-

ход от всей группы предприятий за весь период времени

Т был максимальным.

Эта задача является многошаговой. Шагом управления здесь будет

хозяйственный год. Управление процессом состоит в перераспределении

средств в начале каждого хозяйственного года.

Обычно методами динамического программирования оптимизируют ра-

боту управляемых систем, эффект которой оценивается аддитивной целевой

функцией.

Аддитивной называется функция многих переменных f(x

1

, x

2

, …, x

n

)

вида

∑

=

n

j

jjn

xfxxxf

1

21

),(=),,,( …

ЛАБОРАТОРНАЯ РАБОТА 5. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ

Краткие теоретические сведения



Моделирование процессов и объектов в металлургии. Лаб. практикум

-60-

где каждая функция f

j

зависит только от одной переменной х

j

. Слагаемые ад-

дитивной целевой функции соответствуют эффекту решений, принимаемых

на отдельных этапах управляемого процесса.

Отметим, что есть многошаговые задачи, естественным образом рас-

падающиеся на отдельные этапы, но имеются и задачи, в которых разбиение

приходится вводить искусственно.

П

р

и

н

ц

и

п

о

п

т

и

м

а

л

ь

н

о

с

т

и

р

е

к

у

р

е

н

т

н

о

е

с

о

т

н

о

ш

е

н

и

е

Динамическое программирование как научное направление возникло

и сформировалось в 1951–1953 гг. благодаря работам Р. Беллмана и его со-

трудников. Метод динамического программирования позволяет одну задачу

со многими переменными заменить рядом последовательно решаемых задач

с меньшим числом переменных. Процесс решения задачи разбивается на ша-

ги. При этом если задано начальное состояние управляемой системы, то ну-

мерация шагов осуществляется от конца к началу, а если конечное, то – от

начала к концу.

Основным принципом, на котором ба

зируется оптимизация многоша-

гового процесса и особенности вычислительного метода динамического про-

граммирования, является

принцип оптимальности Р. Беллмана [2, 3].

Приведем его формулировку:

оптимальное поведение обладает тем

свойством, что каковы бы ни были начальное состояние и начальное реше-

ние, последующие решения должны составлять оптимальное поведение от-

носительно состояния, полученного в результате начального решения.

Этот принцип можно сформулировать и по-другому: оптимальное по-

ведение в многошаговом процессе обладает тем свойством, что какими бы ни

были решение, принятое на последнем шаге, и состояние процесса перед по-

следним шагом, предыдущие решения должны составлять оптимальное отно-

сительно этого состояния поведение.

Принцип оптимальности имеет конструктивный характер и непосред-

ственно у

казывает процедуру нахождения оптимального решения. Матема-

тически он записывается выражением вида

11(1)1

1

( ) = optimum [ ( , ) + ( )],

−++−++

+

nl l l l l n l l

U

l

fS RSU f S (5.1)

l = 0, 1, …, n – 1, где U

l

= ( u

l

(1)

; …; u

l

(m)

) – решение (управление), выбранное

на

l-м шаге; S

l

= (s

l

(1)

; …; s

l

(m)

) – состояние системы на l-м шаге; R

l

– непо-

средственный эффект, достигаемый на

l-м шаге; f

n-l

– оптимальное значение

эффекта, достигаемого за

n – l шагов; n - количество шагов (этапов).

«Optimum» в выражении (5.1)

означает максимум или минимум в зависимо-

сти от условия задачи. Формула (5.1)

носит название уравнения Беллмана или

рекуррентного соотношения.

Процесс вычислени f

n-l

, l = 0, …, n – 1, осуще-

ствляется при естественном начальном условии

f

0

(S

n

) = 0, которое означает,

что за пределами конечного состояния системы эффект равен нулю.

Любанова А.Ш. и др. Моделирование процессов и объектов в металлургии. Практикум

Подождите немного. Документ загружается.