Любанова А.Ш. и др. Моделирование процессов и объектов в металлургии. Практикум

Подождите немного. Документ загружается.

ЛАБ. Р. 1. ОПР-Е ПАРАМЕТРОВ РЕГРЕСС. МОДЕЛИ ПО ЭКСПЕРИМЕНТ-М ДАННЫМ МЕТОДОМ НАИМЕНЬШИХ КВАДР

ТОВ

Краткие теоретические сведения



Моделирование процессов и объектов в металлургии. Лаб. практикум

-11-

Корреляция – это связь между двумя или несколькими величинами

или исследуемыми объектами. Корреляция бывает двух видов: детерминиро-

ванная (определяется строгими закономерностями и обычно описывается физи-

ко-химическими формулами) и стохастическая (случайная, вероятностная –

проявляется в том, что одна из величин влияет на изменение другой измене-

ниями своего закона распределения).

Характеристикой системы двух случайных величин, о

писывающей

связь между ними, является коэффициент корреляции

(

)

(

)

MXmYm

⎡

⎤

−−

⎣

⎦

σσ

где

, m

– сокращенное обозначение математического ожидания величины

Х и Y соответственно, m

= M[X], m

= M[Y]. Если r

= 0, то корреляционная

связь между величинами отсутствует.

Зависимость между случайными величинами называется

регрессией.

Она понимается как зависимость между математическими ожиданиями этих

величин.

Форма связи между случайными величинами определяется линией

регрессии, показывающей, как в среднем изменяется величина

Y при измене-

нии величины

Х, что характеризуют условным математическим ожиданием

y/x

величины Y, вычисляемым при Х = х. Таким образом, кривая регрессии Y

на

Х есть зависимость условного математического ожидания Y от известного

значения

Х.

Задача

регрессионного анализа ставится следующим образом: для ка-

ждого

i-го опыта имеется набор значений входных параметров X

, X

, …, X

и соответствующего этому набору значений выходного параметра

Необходимо определить зависимость выходного параметра

Y от вход-

ных факторов

, X

, …, X

, которая в случае, например, линейной связи

может иметь следующий вид:

Y = b

+ b

+ …+ b

Такая зависимость называется

линейной регрессией. Любая другая зависи-

мость называется

нелинейной регрессией.

Задача сводится к тому, чтобы при измеренных во время опытов зна-

чениях входных переменных

, X

, …, X

и выходной переменной Y найти

коэффициенты уравнения регрессии

, b

, …, b

, которые с определенной

степенью вероятности будут отражать влияние аргументов

, X

,…, X

на Y.

ЛАБ. Р. 1. ОПР-Е ПАРАМЕТРОВ РЕГРЕСС. МОДЕЛИ ПО ЭКСПЕРИМЕНТ-М ДАННЫМ МЕТОДОМ НАИМЕНЬШИХ КВАДР

ТОВ

Краткие теоретические сведения



Моделирование процессов и объектов в металлургии. Лаб. практикум

-12-

Регрессионная зависимость вида Y = f(X

) называется однофакторной

или парной и описывает связь между двумя переменными: входной Х и вы-

ходной

Регрессионная зависимость вида

Y = f(X

, X

, …, X

) называется мно-

гофакторной

или множественной и описывает связь между несколькими

входными

, X

, …, X

и одной выходной Y.

Построение и исследование регрессионной модели можно разбить на

четыре этапа.

. Проверка наличия стохастической связи между исследуемыми ве-

личинами. Для этого нужно определить по значению

, существует ли кор-

реляционная связь между

Х и Y.

. Выбор вида уравнения регрессии. Вид уравнения регрессии выби-

рается исходя из особенностей изучаемой системы случайных величин. Один

из возможных подходов при этом – экспериментальный подбор типа уравне-

ния регрессии по соответствующим критериям адекватности. В случае же,

когда имеется определенная априорная (доопытная) информация об объекте,

более эффективным является использование для этой цели теоретических

представлений о процессах и типах свя

зей между изучаемыми параметрами.

. Расчет параметров (коэффициентов) уравнения регрессии. Для оп-

ределения параметров (коэффициентов) уравнения регрессии используется

метод наименьших квадратов (МНК). Сущность метода заключается в том,

что выбирается такая линия регрессии, при которой сумма квадратов разно-

стей между экспериментальными значениями выходной переменной

, по-

лученными на объекте, и значениями, рассчитанными по выбранной регрес-

сионной формуле (модели) )(

XfY = , будет минимальной:

()

min

⇒−=

∑

YYq ,

где q – критерий близости модели и объекта, называемый невязкой модели;

n – количество экспериментальных данных.

Задача построения линейной модели сводится к минимизации функ-

ции невязки следующего вида:

[]

min)...(

22110

⇒++++−=

∑

niniii

xbxbxbbYq .

В качестве нелинейных регрессионных моделей чаще всего исполь-

зуются полиномы разной степени:

= b

+ b

+ …+ b

m-1

4. Проверка адекватности структуры модели. Об адекватности струк-

туры модели можно судить по коэффициенту корреляции

или корреляци-

ЛАБ. Р. 1. ОПР-Е ПАРАМЕТРОВ РЕГРЕСС. МОДЕЛИ ПО ЭКСПЕРИМЕНТ-М ДАННЫМ МЕТОДОМ НАИМЕНЬШИХ КВАДР

ТОВ

Краткие теоретические сведения



Моделирование процессов и объектов в металлургии. Лаб. практикум

-13-

онному отношению η, гистограмме распределения остатков и содержатель-

ному анализу остатков модели [7

, 9].

Коэффициент корреляции r характеризует степень тесноты линей-

ной связи между

и Y, приближенное значение r определяется по формуле

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

−

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

−

∑∑∑∑

∑∑∑

====

===

iiii

YYnYYn

YYYYn

111

где n – число экспериментальных данных. Коэффициент корреляции изменя-

ется от –1 до +1.

Корреляционное отношение η характеризует степень тесноты нели-

нейной связи между переменными

и Y:

()

∑

−

где

– текущее значение, вычисленное по математической модели значение

параметра Y; Y

– текущее значение, полученное на объекте; Y – выборочное

среднее значение,

∑

Корреляционное отношение изменяется от 0 до +1.

Следует иметь в виду, что коэффициент корреляции является част-

ным случаем корреляционного отношения и используется обычно только

при исследовании линейных моделей. Диапазон изменения коэффициента

корреляции (корреляционного отношения) указывает на корреляцию (связь)

между

и Y.

Выводы о степени адекватности модели делаются не только на осно-

вании значения коэффициента корреляции или корреляционного отношения,

но и на основании гистограммы распределения и содержательного анализа

остатков модели.

ЛАБ. Р. 1. ОПР-Е ПАРАМЕТРОВ РЕГРЕСС. МОДЕЛИ ПО ЭКСПЕРИМЕНТ-М ДАННЫМ МЕТОДОМ НАИМЕНЬШИХ КВАДР

ТОВ

Краткие теоретические сведения



Моделирование процессов и объектов в металлургии. Лаб. практикум

-14-

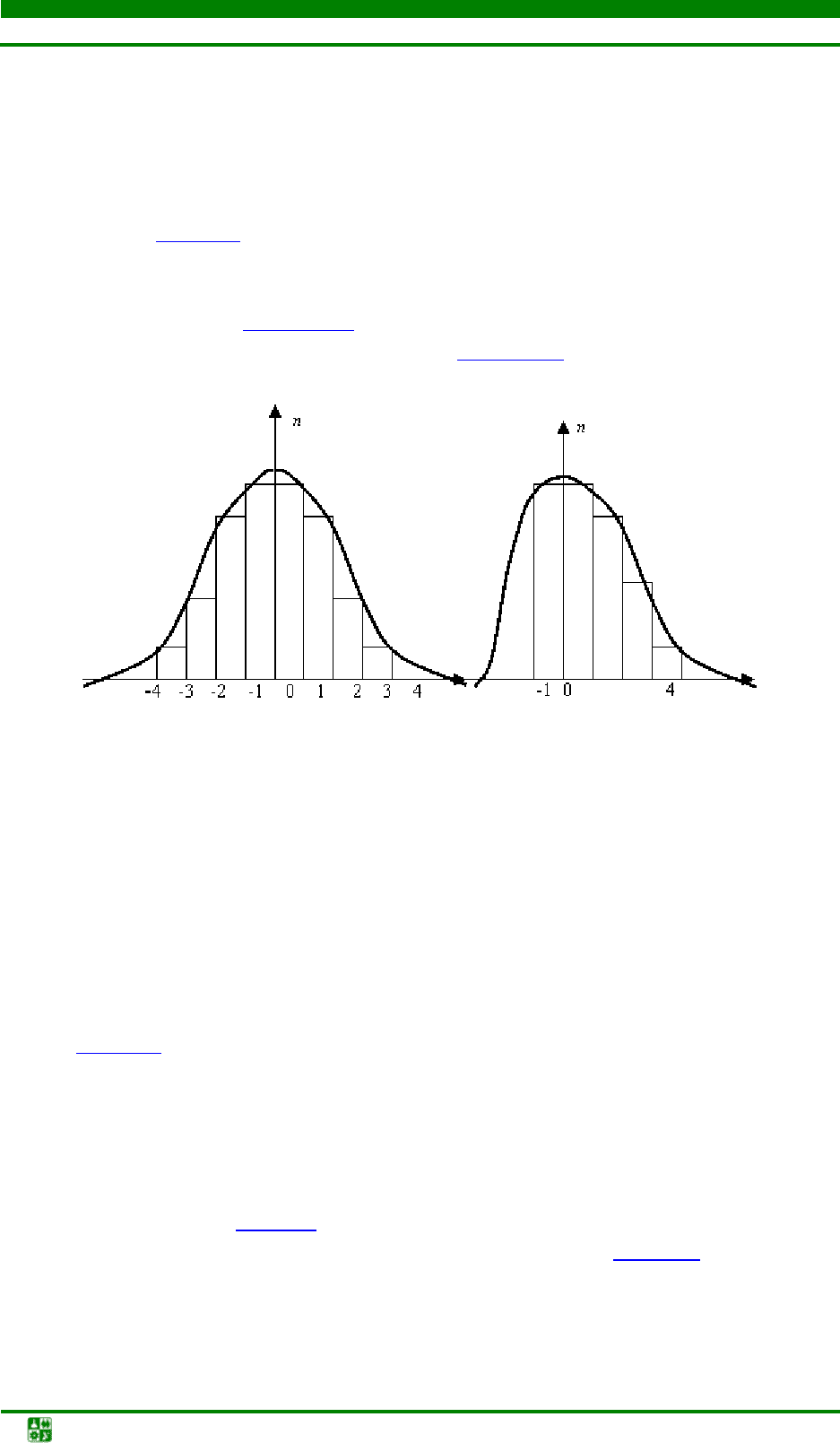
Гистограмма распределения остатков модели строится следующим

образом. Весь диапазон изменения остатков (от минимального из остатков до

максимального) разбивается на несколько равных интервалов, или поддиапа-

зонов (обычно от 6 до 20), которые откладываются на оси абсцисс. Далее на

оси ординат отмечается число попаданий остатка в каждый интервал, или

поддиапазон (рис. 1.1

). Число попаданий ошибки можно откладывать как в

натуральных показателях, так и в процентном соотношении. При адекватно-

сти модели реальному объекту гистограмма распределения приобретает ко-

локолообразный вид (рис. 1.1,

а), при неадекватности модели она имеет не-

симметричный характер или второй горб (рис. 1.1,

б).

а б

Рис. 1.1. Гистограмма распределения остатков

Содержательный анализ остатков модели состоит в построении

распределения остатков модели в зависимости от входного параметра

Попадание большинства данных в горизонтальную полосу, расположенную

симметрично оси

OX, свидетельствует об адекватности модели.

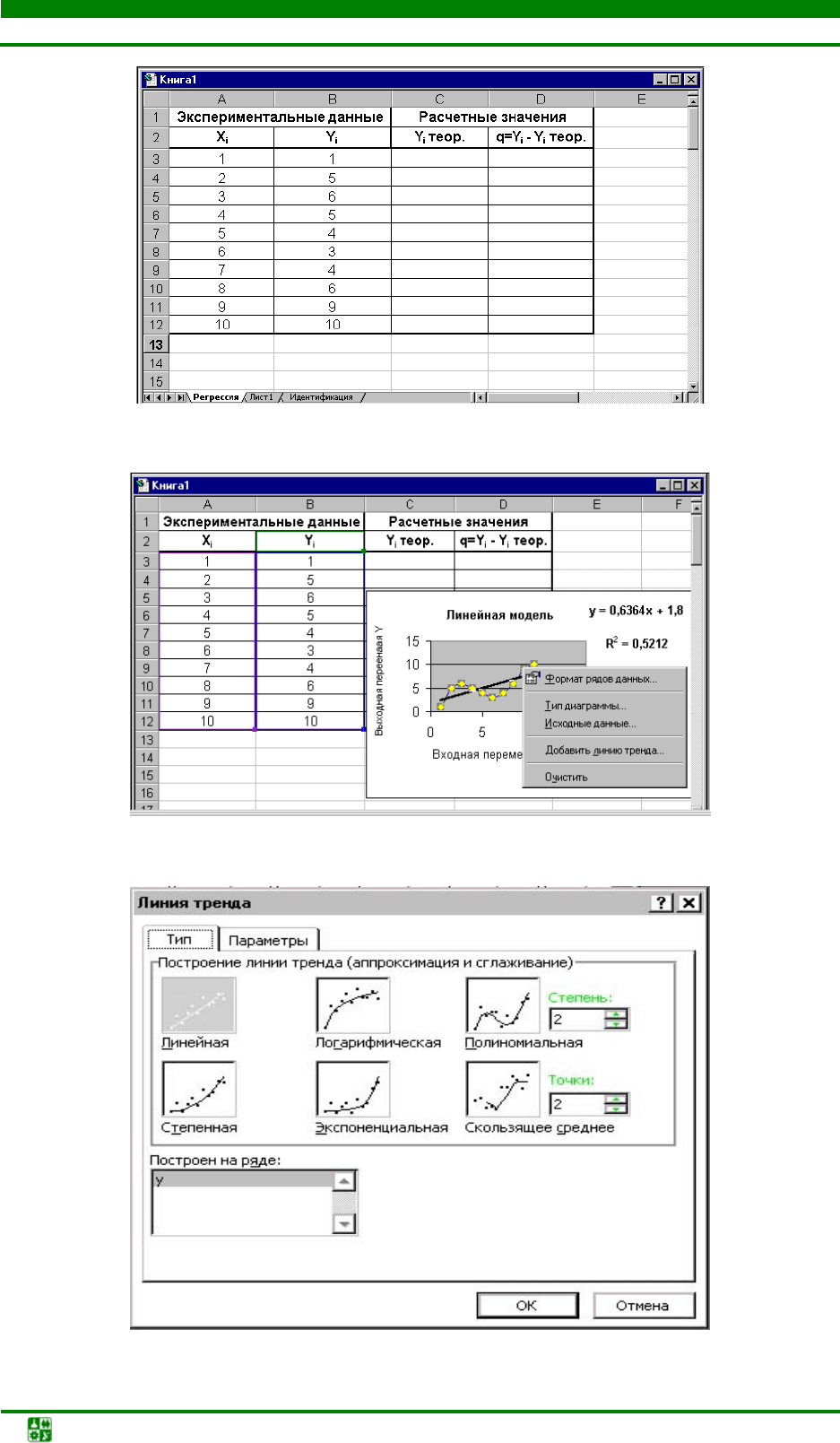
1. Для оформления решения составить таблицу в ППП Microsoft Office

Excel (рис. 1.2

) и, исходя из задания, занести экспериментальные данные в

ячейки A3:B12.

2. Построить точечный график по диапазону ячеек A3:B12, выделить

точки графика щелчком левой кнопки мыши в диапазоне точек на графике, а

затем щелкнуть на них правой кнопкой.

В раскрывшемся контекстном меню следует выбрать команду

Доба-

вить линию тренда

(рис. 1.3).

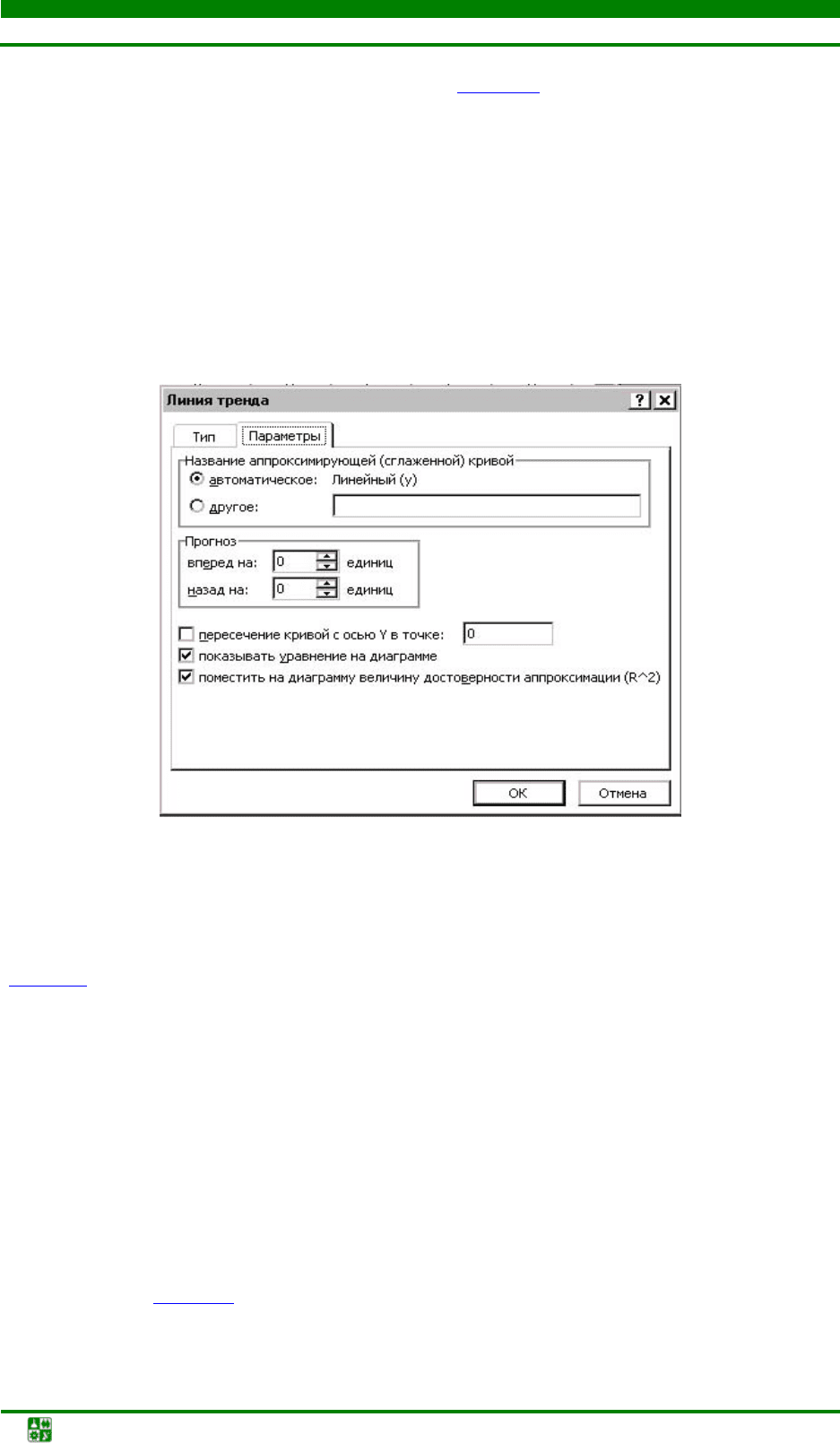
В диалоговом окне

Линия тренда (Trendline) (рис. 1.4) на вкладке

Тип (Type) в группе Построение линии тренда (аппроксимация и сглажи-

вание)

(Trend/Regression type) выбрать параметр Линейная (Linear).

ЛАБ. Р. 1. ОПР-Е ПАРАМЕТРОВ РЕГРЕСС. МОДЕЛИ ПО ЭКСПЕРИМЕНТ-М ДАННЫМ МЕТОДОМ НАИМЕНЬШИХ КВАДР

ТОВ

Порядок выполнения работы



Моделирование процессов и объектов в металлургии. Лаб. практикум

-15-

Рис. 1.2. Таблица данных объекта и модели

Рис. 1.3. Вызов через контекстное меню линии тренда

Рис. 1.4. Вкладка Тип диалогового окна Линия тренда

ЛАБ. Р. 1. ОПР-Е ПАРАМЕТРОВ РЕГРЕСС. МОДЕЛИ ПО ЭКСПЕРИМЕНТ-М ДАННЫМ МЕТОДОМ НАИМЕНЬШИХ КВАДР

ТОВ

Порядок выполнения работы



Моделирование процессов и объектов в металлургии. Лаб. практикум

-16-

На вкладке Параметры (Options) (рис. 1.5) установить флажки Пока-

зывать уравнение на диаграмме

(Display Equation on Chart) и Поместить

на диаграмму величину достоверности аппроксимации

(R^2) (Display R-

squared), т.е. на диаграмму необходимо поместить значение квадрата коэф-

фициента корреляции. В разделе

Прогноз на вкладке Параметры диалогово-

го окна

Линия тренда можно задать параметры вперед и назад для составления

прогноза поведения функции. Флажок

Пересечение кривой с осью Y в точке

(Set Intercept) устанавливается только в том случае, если эта точка известна.

Например, если этот флажок установлен и в его поле введен 0, это означает,

что ищется модель

y = b

Рис. 1.5. Вкладка Параметры диалогового окна

Линия тренда

Результат выполнения команды

Линия тренда представлен на

(рис. 1.6

3. По приведенному выше алгоритму выполнить регрессионный ана-

лиз для нелинейных моделей, в частности построить полиномиальную мо-

дель второго порядка, последовательно увеличить порядок уравнения до

шестого. Для этого выделить линию тренда с помощью щелчка левой кнопки

и вызвать контекстное меню с помощью правой кнопки мыши. Выбрать оп-

цию

Формат линии тренда, далее выбрать соответствующий параметр По-

линомиальная модель

, увеличить показатель степени, найти уравнение и

коэффициент корреляции.

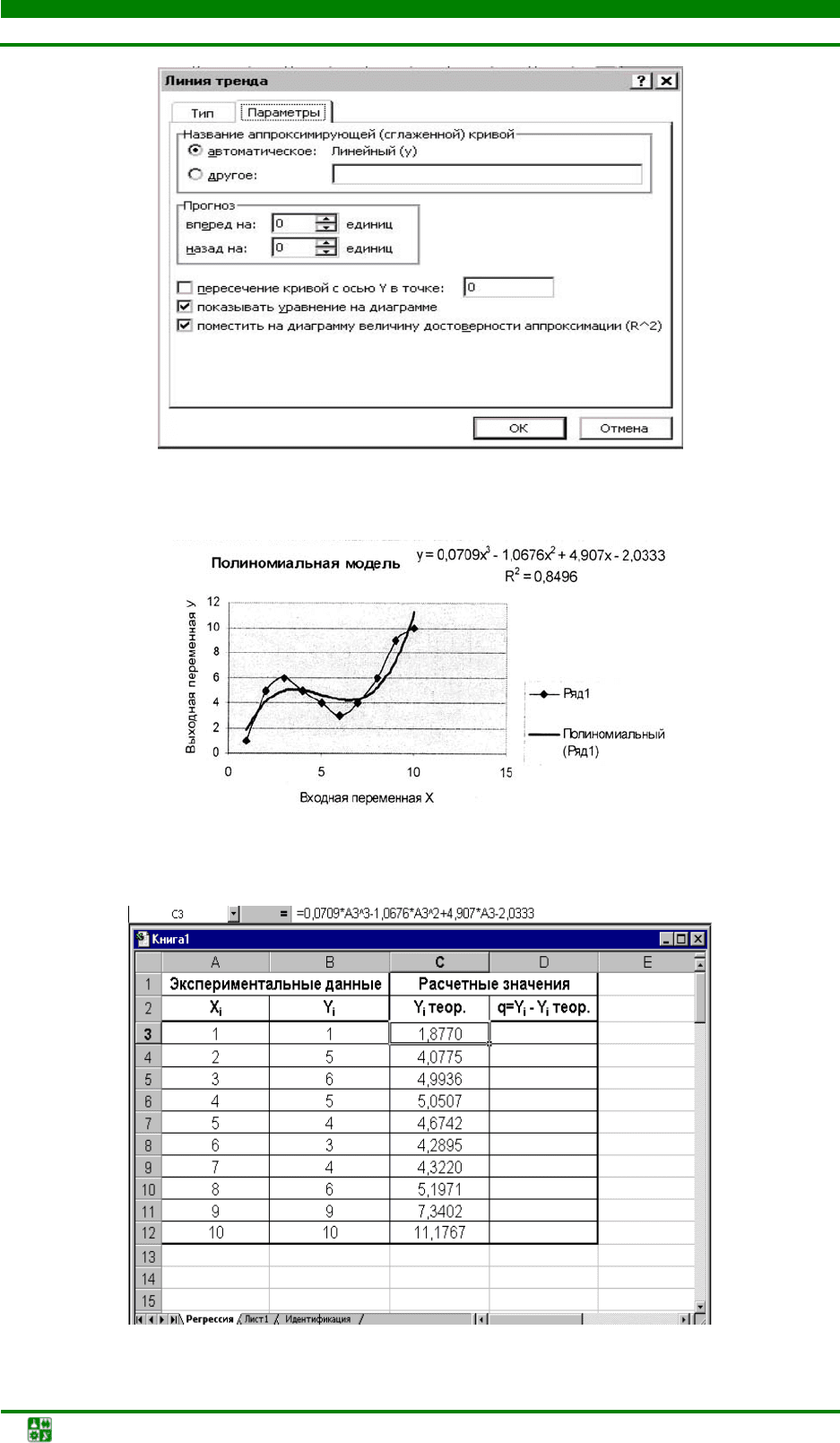
4. Проанализировать полученные данные и по наиболее высокому

значению коэффициента корреляции определиться с типом модели, адекват-

ным объекту (рис. 1.7

ЛАБ. Р. 1. ОПР-Е ПАРАМЕТРОВ РЕГРЕСС. МОДЕЛИ ПО ЭКСПЕРИМЕНТ-М ДАННЫМ МЕТОДОМ НАИМЕНЬШИХ КВАДР

ТОВ

Порядок выполнения работы



Моделирование процессов и объектов в металлургии. Лаб. практикум

-17-

Рис. 1.6. График линии тренда линейной модели

Рис. 1.7. Выбранная полиномиальная модель

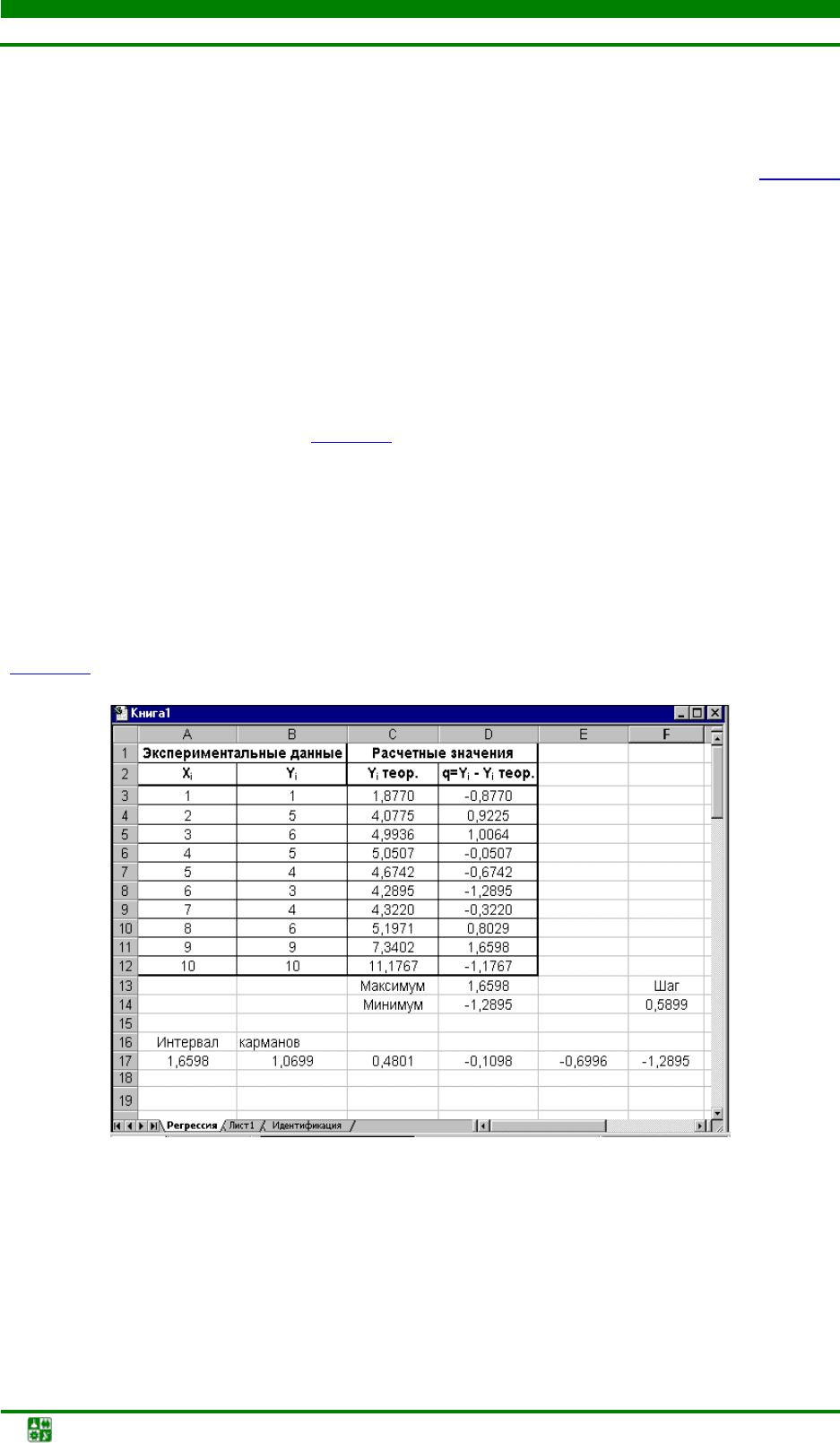
Рис. 1.8. Нахождение теоретических значений

ЛАБ. Р. 1. ОПР-Е ПАРАМЕТРОВ РЕГРЕСС. МОДЕЛИ ПО ЭКСПЕРИМЕНТ-М ДАННЫМ МЕТОДОМ НАИМЕНЬШИХ КВАДР

ТОВ

Порядок выполнения работы



Моделирование процессов и объектов в металлургии. Лаб. практикум

-18-

5. На основе найденных коэффициентов уравнения регрессии устано-

вить теоретическое значение наблюдаемой величины

Y. Для этого нужно рас-

считать теоретическое значение

Y в ячейке C3, заменяя X на A3 по формуле, по-

лученной в результате регрессионного анализа, например, у модели на рис. 1.5

формула для вычисления имеет вид

= - 0,0709*А3^3-1,0676*A3^2+4,907*A3-2,0333.

Скопировать значение ячейки C3 на весь столбец C, используя контекстное

меню или панель инструментов.

6. Вычислить ошибку модели в ячейке D3 по формуле =B3-C3 и ско-

пировать на весь столбец D (рис. 1.8

7. Для проверки модели на адекватность построить гистограмму рас-

пределения ее остатков. Это сделать следующим образом. Составить диапа-

зон изменения остатков, определить их минимальное и максимальное значе-

ния с помощью функций

МАКС() и МИН(). Затем весь диапазон изменения

остатков разбить на несколько равных поддиапазонов (от 6 до 20) и рассчи-

тать число попаданий ошибки (остатков) в каждый поддиапазон.

Все границы интервалов записать в отдельную строку или столбец

(рис. 1.9

Рис. 1.9. Нахождение ошибки и карманов

Далее для построения гистограммы распределения остатков выбрать

команду

Сервис, Анализ данных (если этой опции не будет, необходимо

выбрать команду

Надстройки... и в появившемся диалоговом окне отметить

флажком опцию

Пакет анализа). В появившемся диалоговом окне Анализ

данных

в разделе Инструменты анализа выбрать опцию Гистограмма.

ЛАБ. Р. 1. ОПР-Е ПАРАМЕТРОВ РЕГРЕСС. МОДЕЛИ ПО ЭКСПЕРИМЕНТ-М ДАННЫМ МЕТОДОМ НАИМЕНЬШИХ КВАДР

ТОВ

Порядок выполнения работы



Моделирование процессов и объектов в металлургии. Лаб. практикум

-19-

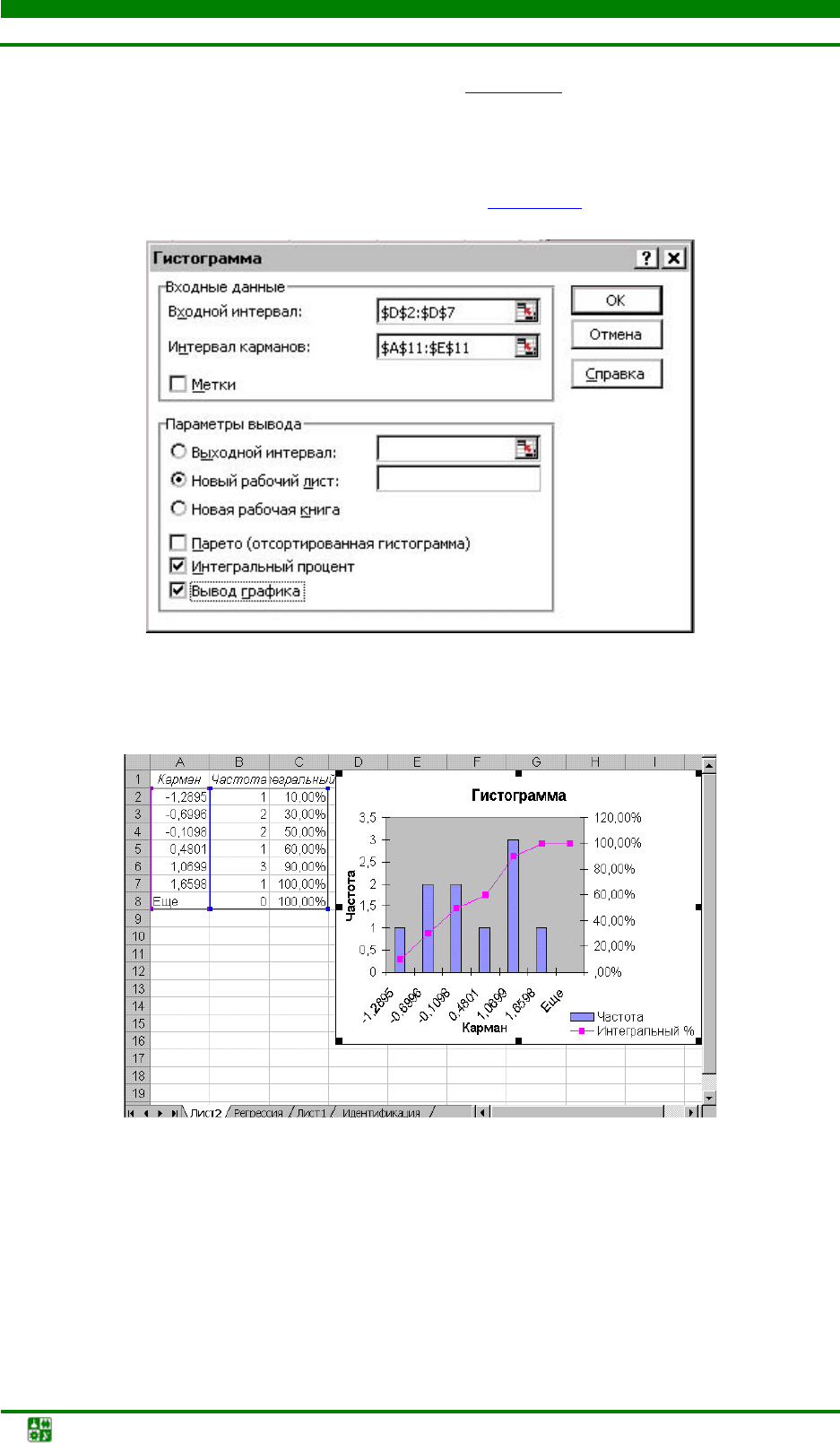
В диалоговом окне Гистограмма (рис. 1.10) в поле Входной интер-

вал

выбрать интервал, в котором находится диапазон ошибок (D3:D12), в

поле

Интервал карманов – диапазон значений отрезков поддиапазонов. От-

метить флажками

Интегральный процент и Вывод графика.

Результаты построения приведены на рис. 1.11

Рис. 1.10. Построение гистограммы распределения остатков модели

Рис. 1.11. Гистограмма распределения остатков

8. Для проверки модели на адекватность построить график содержа-

тельного анализа остатков модели в зависимости от входной переменной

Х.

Построить точечный график по диапазону ячеек в столбцах A3:A12 и

D3:D12. По полученным результатам сделать выводы об адекватности по-

строения модели экспериментальным данным и оформить отчет.

ЛАБ. Р. 1. ОПР-Е ПАРАМЕТРОВ РЕГРЕСС. МОДЕЛИ ПО ЭКСПЕРИМЕНТ-М ДАННЫМ МЕТОДОМ НАИМЕНЬШИХ КВ

ДР

ТОВ



Моделирование процессов и объектов в металлургии. Лаб. практикум

-20-

Варианты 1–9

Определить зависимость предела прочности сплава (варианты 1–3), пре-

дела текучести (варианты 4–6) или относительного удлинения (варианты 7–9)

сплава В95 от времени искусственного старения, используя данные табл. 1.1

Таблица 1.1

Номер варианта Температура,

С График

1 120

2 135

3 150

4 135

0 4 8 1216202428323640

Старение, ч

Предел прочности, кг/мм

0 4 8 12 16 20 24 28 32 36 40

Старение, ч

Предел прочности, кг/мм

0 4 8 1216202428323640

Старение, ч

Предел прочности, кг/мм

0 4 8 12 16 20 24 28 32 36 40

Стар ение, ч

Предел текучести, кг/мм