Любанова А.Ш. и др. Моделирование процессов и объектов в металлургии. Практикум

Подождите немного. Документ загружается.

ЛАБ. Р. 1. ОПР-Е ПАРАМЕТРОВ РЕГРЕСС. МОДЕЛИ ПО ЭКСПЕРИМЕНТ-М ДАННЫМ МЕТОДОМ НАИМЕНЬШИХ КВАДР

ТОВ

Задание



Моделирование процессов и объектов в металлургии. Лаб. практикум

-21-

Продолжение табл. 1.1

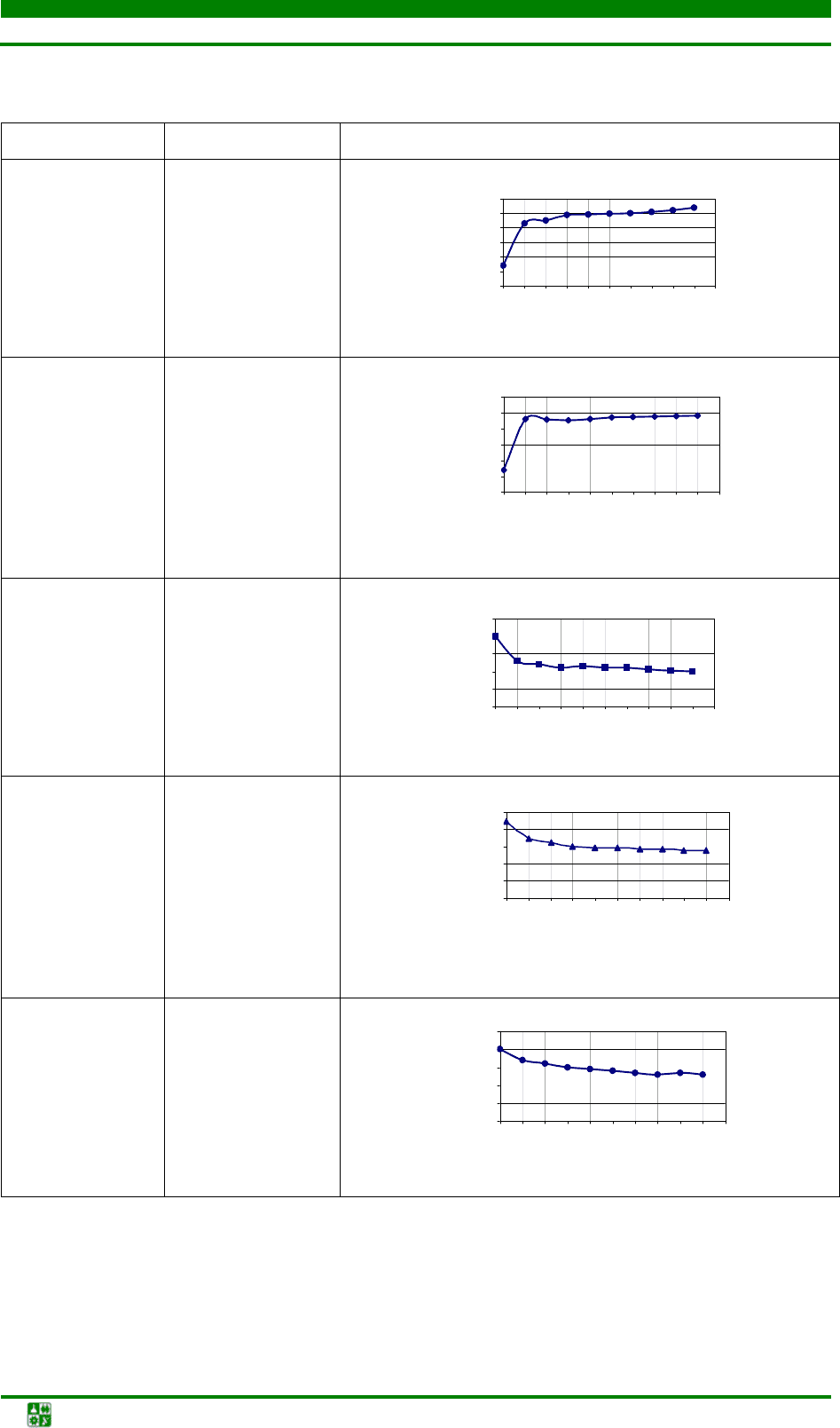
Номер варианта Температура,

С График

5 120

6 150

7 150

8 135

9 120

0 4 8 12 16 20 24 28 32 36 40

Старение, ч

Предел текучести, кг/мм

0 4 8 1216202428323640

Старение, ч

Предел текучести, кг/мм

0 4 8 1216202428323640

Старение, ч

Относительн.

удлинение,%

0 4 8 12 16 20 24 28 32 36 40

Стар ен ие, ч

Относительн. удл и н ение,%

0 4 8 12 16 20 24 28 32 36 40

Старение, ч

Относительн.удлинение,%

ЛАБ. Р. 1. ОПР-Е ПАРАМЕТРОВ РЕГРЕСС. МОДЕЛИ ПО ЭКСПЕРИМЕНТ-М ДАННЫМ МЕТОДОМ НАИМЕНЬШИХ КВАДР

ТОВ

Задание



Моделирование процессов и объектов в металлургии. Лаб. практикум

-22-

Вариант 10–12

Определить зависимость изменения глубины диффузионного слоя нио-

бия при нагреве в течение 1 ч на воздухе до указанной температуры (табл. 1.2

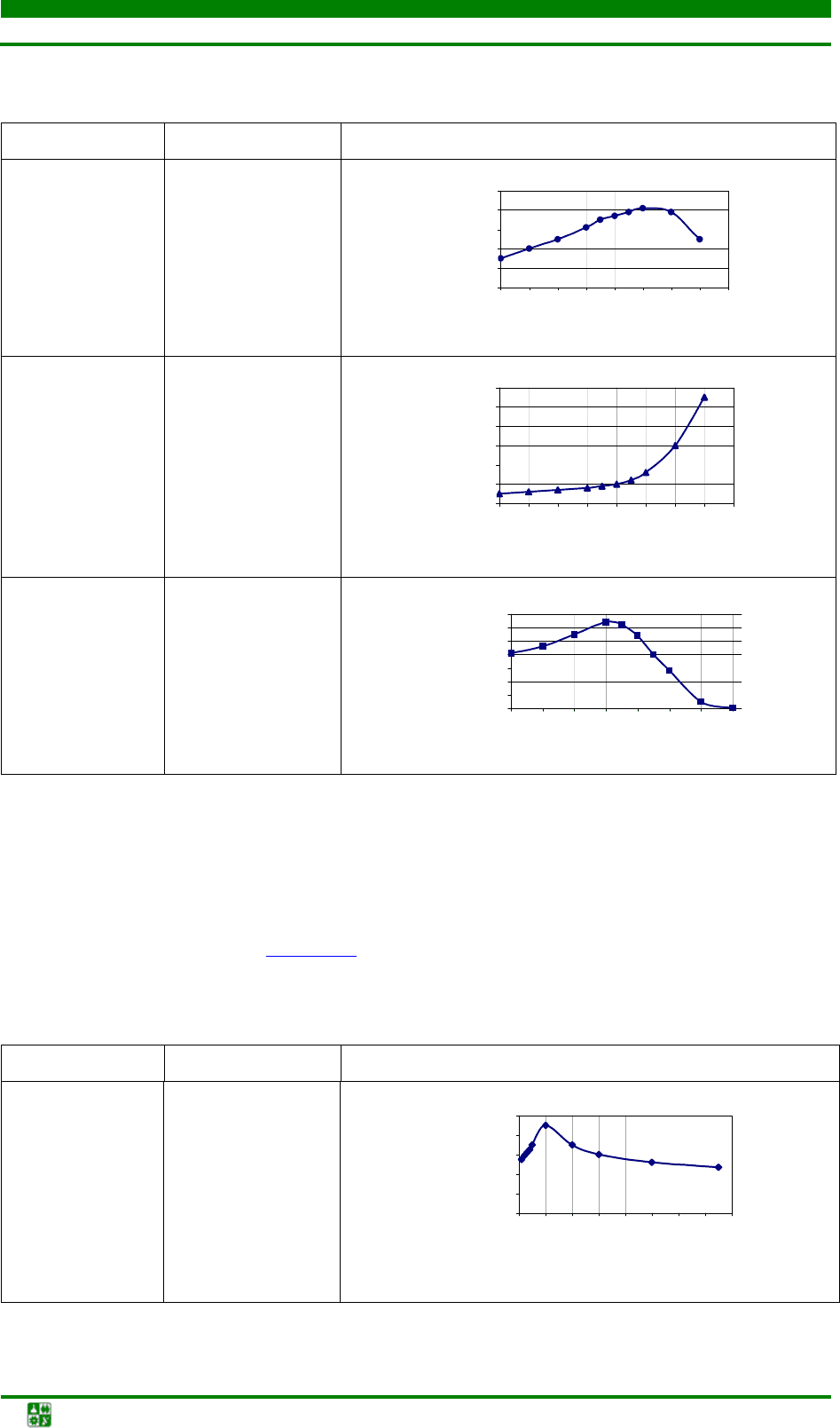
Таблица 1.2

Номер варианта Температура,

С График

10 1 200

100

200

300

400

500

600

700

800

0 0,08 0,16 0,24 0,32 0,4 0,48

Расстояние от поверхности, мм

Микротвердость, кг/мм

11 1 000

12 800

Вариант 13–16

Для кремнистых бронз определить зависимость указанного параметра

от содержания кремния (табл. 1.3

Таблица 1.3

Номер варианта Параметр График

13 Твердость

100

200

300

400

500

600

700

0 0,08 0,16 0,24 0,32 0,4 0,48

Расстояние от поверхности, мм

Микротвердость, кг/мм

100

200

300

400

500

600

700

800

0 0,08 0,16 0,24 0,32 0,4 0,48

Расстояние от поверхности, мм

Микротвердость, кг/мм

100

150

200

250

012345678

Содержание Si, %

Твердость, кг/мм

ЛАБ. Р. 1. ОПР-Е ПАРАМЕТРОВ РЕГРЕСС. МОДЕЛИ ПО ЭКСПЕРИМЕНТ-М ДАННЫМ МЕТОДОМ НАИМЕНЬШИХ КВАДР

ТОВ

Задание



Моделирование процессов и объектов в металлургии. Лаб. практикум

-23-

Продолжение табл. 1.3

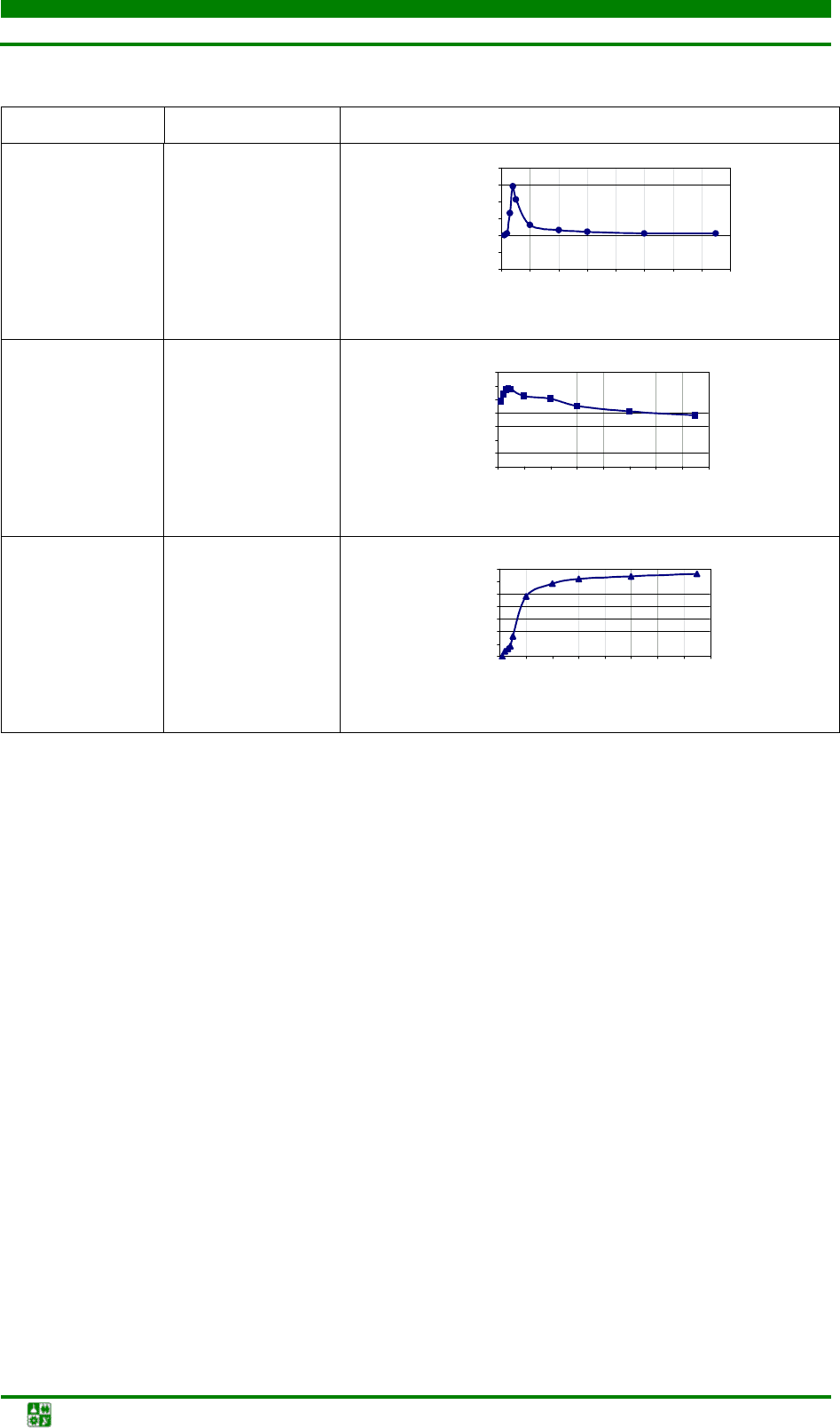
Номер варианта Параметр График

Предел

прочности

Предел

текучести

Относительное

удлинение

Вариант 17–20

Для сплавов цинка определить зависимость указанного параметра от

естественного старения (табл. 1.4

Таблица 1.4

Номер варианта Параметр График

Твердость

012345678

Содержание Si, %

Предел прочности кг/мм

012345678

Содержание Si, %

Предел текучести, кг/мм

100

0 1020304050607080

Время выдержки, мин

Твердость, кг/мм

01234567

Содержание Si, %

Относительн.удлинение,%

ЛАБ. Р. 1. ОПР-Е ПАРАМЕТРОВ РЕГРЕСС. МОДЕЛИ ПО ЭКСПЕРИМЕНТ-М ДАННЫМ МЕТОДОМ НАИМЕНЬШИХ КВАДР

ТОВ

Задание



Моделирование процессов и объектов в металлургии. Лаб. практикум

-24-

Продолжение табл. 1.4

Номер варианта Параметр График

18 Температура

Электросопро-

тивление

Изменение

длины

1. Дайте определения математической модели и объекта.

В чем заключается задача регрессионного анализа?

Какую величину называют случайной? Опишите основные типы

случайных величин.

Сформулируйте закон распределения случайной величины.

Назовите виды регрессионных зависимостей.

Какая характеристика служит для оценки качества линейной моде-

ли? Какие она может принимать значения?

Описать сущность МНК.

Какая характеристика служит для оценки качества нелинейной мо-

дели? Какие она может принимать значения?

Дайте определение корреляции. Какие виды корреляции вы знаете?

10.

Можно ли считать, что математическая модель и линия регрессии

одно и то же? Как строится линия регрессии?

11.

Опишите метод построения гистограммы.

12.

В чем заключается содержательный анализ остатков модели?

13.

В каких случаях используется корреляционный коэффициент, а в

каких – корреляционное отношение как критерий адекватности модели?

14.

Назовите этапы построения и исследования регрессионной моде-

ли.

15.

Каковы методы проверки адекватности структуры модели?

0 1020304050607080

Время выдержки, мин

Температура,

01020304050607080

Время выдержки, мин

Электросопротивление,Ом х10

0,05

0,1

0,15

0,2

0,25

0,3

0,35

0 1020304050607080

Время выдержки, мин

Изменение длины,%



Моделирование процессов и объектов в металлургии. Лаб. практикум

-25-

Ознакомиться с методами оптимизации и численными алгоритмами

для решения задач безусловной оптимизации; научиться решать задачи без-

условной оптимизации с использованием пакетов прикладных программ на

ЭВМ; научиться анализировать полученные

результаты.

Решение всякой задачи оптимизации начинается с ее математической

постановки.

Общая постановка задачи состоит в следующем.

Задано: множество X и функция f(x), определённая на Х.

Требуется: найти точки минимума или максимума функции f на X.

Будем записывать задачу на минимум в виде

f(x) → min, х ∈ X. (2.1)

Задача (2.1)

сформулирована как задача нахождения минимума функ-

ции

f(x), или минимизации f(x). На практике же приходится сталкиваться как

с задачами минимизации, так и с задачами

максимизации f(x), т.е. нахожде-

ния точек максимума

f(x):

f(x) → max, х ∈ Х.

С математической точки зрения различия между задачами минимиза-

ции и максимизации не существенны, поскольку максимизация

f(x) эквива-

лентна минимизации функции −

f(x). Поэтому всегда можно ставить задачу

оптимизации как задачу минимизации (2.1)

Функция

f(x) в выражении (2.1), т.е. функция, которую мы минимизи-

руем, называется

целевой. Множество Х в формуле (2.1), на котором мы ми-

нимизируем

f(x), называется допустимым множеством задачи, а любой эле-

мент

х ∈ Х − допустимой точкой задачи. Допустимая точка х*∈Х, в которой

ЛАБОРАТОРНАЯ РАБОТА 2. МЕТОДЫ БЕЗУСЛОВНОЙ ОПТИМИЗАЦИИ

Краткие теоретические сведения



Моделирование процессов и объектов в металлургии. Лаб. практикум

-26-

целевая функция f(x) достигает своего минимума, называется решением зада-

чи.

Следует иметь в виду, что на практике допустимая точка

х может

представлять собой некоторый набор параметров

х = (х

, ..., х

). Причём зна-

чения этих параметров могут подчиняться ограничениям или изменяться без

ограничений. Если, например,

выражает количество производимого про-

дукта

i-го вида (сплав соответствующей марки и пр.) для каждого i = 1, ..., n,

то при этом будет существовать ограничение на производственную мощ-

ность (например, 0 ≤

≤ а

, i = 1, ..., n) и ограничение на количество товара,

которое может поглотить рынок (например, α

+ α

+ … + α

≤ b, где α

– рыночная цена i-го товара; b – общая денежная масса).

Необходимо подчеркнуть, что само понятие точки минимума (реше-

ния задачи (2.1)

) неоднозначно и требует уточнения.

Точка х* ∈ Х называется точкой глобального минимума функции f(x)

на множестве

Х или глобальным решением задачи (2.1), если

f(x*) ≤ f(x) при всех х ∈ Х. (2.2)

Точка

х* ∈ Х называется точкой локального минимума f на Х или

локальным решением задачи (2.1), если существует такое подмножество U

(

х*) = {x⏐x∈ X, || x − x*|| ≤ δ}, что

f(x*) ≤ f(x) при всех x∈U

(x*). (2.3)

Здесь и далее

()

2/1

⎥

⎦

⎤

⎢

⎣

⎡

−=−

∑

∗

xxxx

Очевидно, что глобальное решение является и локальным, обратное

неверно.

Для отражения того факта, что точка x*∈ X является точкой глобаль-

ного минимума функции f на X, будем использовать запись

()=min().

xfx

∗

∈

Если неравенство в (2.2)

или (2.3) выполняется как строгое при x

≠

x*,

т.е. f(x) < f(x*), x

∈ X (или x ∈ U

(x*)), то говорят, что x* – точка строгого ми-

нимума (строгое решение).

При изучении задач оптимизации в первую очередь возникает вопрос о

существовании решения. Условия, гарантирующие разрешимость задачи (2.1)

содержатся в следующей теореме из курса высшей математики [1

, 2, 4].

ЛАБОРАТОРНАЯ РАБОТА 2. МЕТОДЫ БЕЗУСЛОВНОЙ ОПТИМИЗАЦИИ

Краткие теоретические сведения



Моделирование процессов и объектов в металлургии. Лаб. практикум

-27-

Т е о р е м а 1 (Вейерштрасса). Пусть Х – ограниченное замкнутое

множество в

, f(х) – непрерывная функция на Х. Тогда существуют точки

глобального минимума и максимума функции f на Х (глобальное решение за-

дачи (2.1)

Эта теорема отвечает на вопрос о существовании решения, но не даёт

конструктивного алгоритма нахождения этого решения. Следует также учесть,

что задача оптимизации может иметь несколько решений. Вопрос о единствен-

ности решения рассматривается отдельно для каждого класса задач (классифика-

цию задач оптимизации можно найти, например, в учебной литературе [1

, 2]).

При изучении любого типа задач оптимизации важное место занимает

вопрос об

условиях оптимальности, или, как еще говорят, условиях экс-

тремума. Различают необходимые условия оптимальности, т.е. условия, ко-

торым должна удовлетворять точка, являющаяся решением задачи, и доста-

точные условия оптимальности, т.е. условия, из которых следует, что данная

точка является решением задачи. В общем случае суть всех критериев опти-

мальности для задачи (2.1)

заключается в том, что из точки х*, являющейся

локальным решением, нельзя осуществить сколь угодно малый сдвиг в каком

бы то ни было направлении, приводящий к уменьшению значения целевой

функции, и остаться при этом в пределах допустимого множества.

Если допустимое множество Х =

, то задача (2.1) называется зада-

чей безусловной оптимизации

. Приведем ее математическую постановку.

Задано: функция f(х), определенная на

Требуется: найти точки минимума функции f на

. Иначе говоря,

f(х)

→ min, х ∈ R

. (2.4)

Теория необходимых и достаточных условий оптимальности в задачах

безусловной оптимизации излагается в любом курсе высшей математики [2

, 3].

Необходимое условие оптимальности.

Пусть функция f дифференци-

руема в точке х*

∈R

. Если х* – локальное решение задачи (2.4), то все пер-

вые производные функции f в точке х* равны нулю:

()

0, 1, 2, , .

∗

∂

…

Достаточное условие безусловного локального минимума связано со

вторыми производными функции f. При n = 2 наличие экстремума в точке х*

зависит от знака определителя

ЛАБОРАТОРНАЯ РАБОТА 2. МЕТОДЫ БЕЗУСЛОВНОЙ ОПТИМИЗАЦИИ

Краткие теоретические сведения



Моделирование процессов и объектов в металлургии. Лаб. практикум

-28-

() ()

∂∂

∂

∂∂

∂

Пусть функция f дважды дифференцируема в точке х*

∈

и первые

частные производные (градиент) функции f в точке х* равны нулю. Тогда

функция f достигает экстремума в точке x* при D > 0. Причем, если

()

,0*

∂

то х* − точка локального минимума. Если

()

,0*

∂

то х* − точка локального максимума.

Для функции f числового аргумента (n = 1) достаточные условия экстре-

мума означают, что если f

′

(x*) = 0 и f

′′

(x*) > 0, то x* − решение задачи (2.4).

Изучение методов безусловной оптимизации начинается с наиболее

простого типа оптимизационных задач, в которых целевая функция зависит

от одной переменной.

Поскольку универсальных методов, пригодных для минимизации лю-

бых функций одной переменной, не существует, приходится строить алго-

ритмы, ориентированные на различные классы функций, встречающиеся в

прикладных задачах.

Рассмотрим методы одномерной минимизации так называемых уни-

модальны

х функций.

Функция f называется унимодальной на Х, если существует такая точ-

ка х*∈Х, что для любых x

∈ X

f(x

) > f(x

), если х

< x

< x*,

f(x

) < f(x

), если х* < x

< x

Для непрерывных функций свойство унимодальности означает нали-

чие у неё единственного локального минимума. Предположение об унимо-

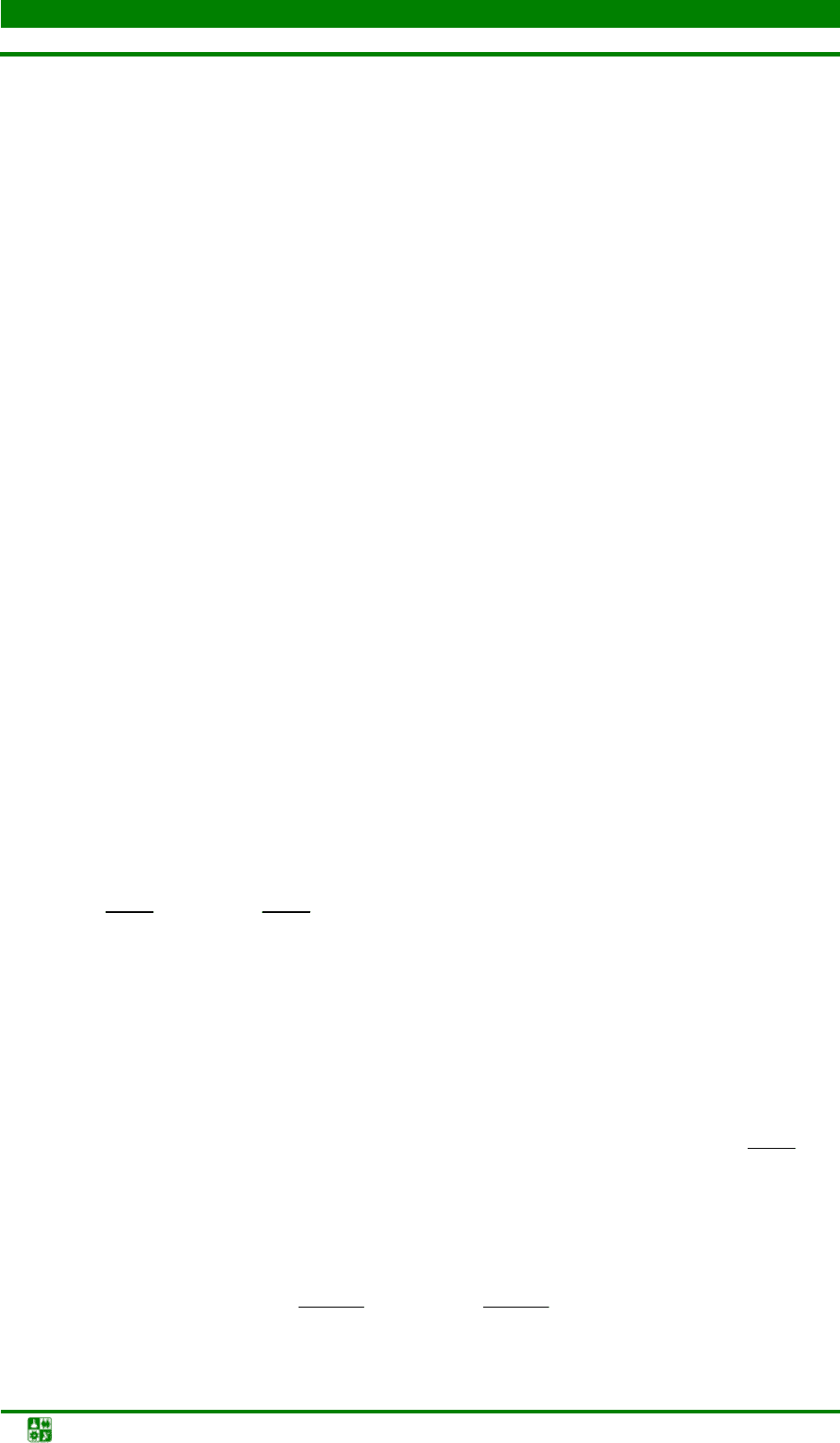
ЛАБОРАТОРНАЯ РАБОТА 2. МЕТОДЫ БЕЗУСЛОВНОЙ ОПТИМИЗАЦИИ

Краткие теоретические сведения



Моделирование процессов и объектов в металлургии. Лаб. практикум

-29-

дальности целевой функции не является жестким ограничением и выполня-

ется во многих практических задачах поиска оптимума.

Если известен какой-либо отрезок [х

, х

], которому принадлежит х*,

будем говорить, что точка минимума х* локализована в отрезке [х

, х

]. Сам

отрезок при этом будем называть отрезком локализации минимума. В лите-

ратуре интервал (х

, х

) называется интервалом неопределённости.

Все методы минимизации унимодальных функций опираются на сле-

дующее утверждение.

Т е о р е м а 2. Пусть функция f унимодальна на Х и х

< x

. Тогда, ес-

ли f(x

) ≤ f(x

), то х* ≤ х

, если же f(x

) ≥ f(x

), то х* ≥ х

, а если f(x

) = f(x

), то

х*∈ [х

, х

Работа любого алгоритма минимизации состоит из двух этапов. На

первом этапе вычисляются предусмотренные алгоритмом характеристики за-

дачи. На втором этапе по полученной информации строится приближение к

решению. Обычно для задания алгоритма достаточно указать способ выбора

точек приближения x

= (х

, …, х

) ∈

, k =1, 2, … Выбор точек приближе-

ния называется поиском точек.

Если все точки выбираются одновременно до начала вычислений, то

алгоритм минимизации называется пассивным. Однако для решения боль-

шинства задач точки приближения выбираются поочередно, т.е. точка х

(k+1)

выбирается тогда, когда уже выбраны точки предыдущих вычислений х

(1)

(2)

, …, х

(k)

и в каждой из них произведены предусмотренные алгоритмом вы-

числения. Такие алгоритмы называются последовательными.

К последовательным методам поиска экстремума унимодальных

функций одной переменной относятся методы исключения интервалов,

включающие методы дихотомии, Фибоначчи, золотого сечения. Простейшим

из них является

метод дихотомии. Его суть состоит в следующем.

Пусть количество допустимых вычислений функции N = 2k. При-

мем

=−δ

=+δ где δ – некоторое положительное число,

δ < (a + b)/2

. Вычислим f(x

) и f(x

) и определим новый отрезок локализации

минимума. Согласно теореме 2, если f(x

) < f(x

), то х*∈ [а, х

]; если f(x

) > f(x

то х*

∈ [x

, b]; если f(x

) = f(x

), то х*

∈

, x

]. В превом случае искомым от-

резком будет [a, x

], во втором − [x

, b], в третьем − [x

, x

Для единообразия в случае f(x

) = f(x

) будем рассматривать в качестве

нового отрезка локализации минимума, например, [a, x

]. Так что длина от-

резка локализации после первой пары вычислений функции равна

−

Вторая пара значений f вычисляется в точках х

, х

, отстоящих на расстоянии

δ по обе стороны от середины нового отрезка локализации. Если, например,

этим отрезком оказался [a, x

], то

δ+

=δ−

ЛАБОРАТОРНАЯ РАБОТА 2. МЕТОДЫ БЕЗУСЛОВНОЙ ОПТИМИЗАЦИИ

Краткие теоретические сведения



Моделирование процессов и объектов в металлургии. Лаб. практикум

-30-

Используя снова те же условия, определяем новый отрезок локализа-

ции минимума длиной

ba−

После N вычислений функции мы нашли отрезок локализации мини-

мума [x

N-1

, x

] длиной

12/

−

−N

на котором расположена точка х*. Величину l называют погрешностью ме-

тода дихотомии. Соответствующим выбором δ величину l можно сделать

сколь угодно близкой к (b – a)/2

N/2

. Приняв приближённо

х*

≈

N-1

+ x

)/2,

получим, что погрешность вычисления х* не превышает величину l/2. Число

f((x

N-1

+ x

)/2) будем считать минимальным значением f(x) на [a, b].

Сравнительный анализ указанных выше методов и обзор других мето-

дов одномерной минимизации можно найти в учебном пособии [1

Методы минимизации функций многих переменных можно разделить

на две группы. Первую группу составляют регулярные методы оптимизации

(или методы направленного поиска). Наиболее важными среди них являются

так называемые методы спуска. Ко второй группе относятся методы случай-

ного поиска.

методах спуска направление движения к минимуму на каждом ша-

ге выбирается из числа направлений убывания минимизируемой функции.

Говорят, что вектор

= (h

, h

, ..., h

) задает направление убывания

функции f в точке x, если существует такое число α

> 0, что

f(x + α

h ) < f(х) (2.5)

при всех 0 < α < α

. Сам вектор h также называют направлением убывания.

Заменив неравенство, фигурирующее в (2.5)

, на противоположное,

получим определение направления возрастания.

Общая идея методов спуска состоит в следующем. Для определения

точки x* локального минимума функции f(x) строится последовательность