Любанова А.Ш. и др. Моделирование процессов и объектов в металлургии. Практикум
Подождите немного. Документ загружается.


ЛАБОРАТОРНАЯ РАБОТА 2. МЕТОДЫ БЕЗУСЛОВНОЙ ОПТИМИЗАЦИИ
Краткие теоретические сведения
Моделирование процессов и объектов в металлургии. Лаб. практикум
-31-
точек {x
(k)
} (k = 0, 1, 2, …), сходящаяся к точке х* таким образом, чтобы по-
следовательность значений функции f(х
(k)
) была монотонно убывающей и ог-
раниченной:
f(x
(0)
) ≥ f(x
(1)
) ≥ … ≥ f(x
(k)
) ≥ … ≥ f(x*).
Для различных методов спуска сначала выбирают начальную точку
последовательности х
(0)
. Дальнейшие приближения x
(k)
определяются соот-
ношениями
x
(k +1)
= x
(k )
+ α
k
⎯h
(k)
(k = 0, 1, 2, …), (2.6)
где ⎯h
(k)
– вектор направления убывания; α
k
– положительная скалярная вели-
чина, называемая длиной шага.
Методы спуска различаются выбором направления убывания и длины
шага. Наиболее известные из них − методы прямого поиска и градиентные
методы.
Методы прямого поиска относятся к алгоритмам нулевого порядка, в
которых используются только значения целевой функции. Мы рассмотрим
подробно только один из них, а именно метод покоординатного спуска, ил
и
метод Гаусса-Зейделя. Практика показала, что этот метод эффективен и
применим для широкого круга приложений.
Решение задачи (2.4)
методом покоординатного спуска осуществляет-
ся по следующей общей схеме.
Выбирают произвольно начальную точку х
(0)
из области определения
функции f(х). Приближения х
(k)
определяются соотношениями (2.6), где век-
тор направления убывания ⎯h
(k)
– это единичный вектор, коллинеарный ка-
кому-либо из координатных направлений; величина α
k
является решением
задачи одномерной минимизации
f(x
(k)
+ t⎯h
(k)
) → min, t ∈ R.
Решение этой задачи может быть найдено, в частности, каким-либо из
методов одномерной минимизации.
Условием прекращения вычислительной процедуры при достижении
заданной точности ε может служить неравенство
|| х
(k + 1)
− х
(k)
|| < ε. (2.7)

ЛАБОРАТОРНАЯ РАБОТА 2. МЕТОДЫ БЕЗУСЛОВНОЙ ОПТИМИЗАЦИИ
Краткие теоретические сведения
Моделирование процессов и объектов в металлургии. Лаб. практикум
-32-
Теоретически данный метод эффективен в случае единственного ми-
нимума функции. Его достоинством является простота алгоритма. Но на
практике он оказывается слишком медленным. Поэтому были разработаны
более сложные методы, использующие информацию не только о значениях
функции, но и ее производных. Это так называемые градиентные методы
спуска.
Далее везде будем считать, что f(x) и ∇ f(x) существуют и непрерыв-
ны, а компоненты градиента могут быть записаны в ан
алитическом виде или
с достаточно высокой точностью найдены с помощью численных методов.
Все градиентные методы основаны на итерационной процедуре, реа-
лизуемой в соответствии с формулой (2.6)
, где вектор h
(k)
строится с помо-
щью антиградиента функции f в точке x
(k)
, т.е. вектора −∇f(x
(k)
), задающего
направление наискорейшего убывания целевой функции f. Способ определе-
ния h
(k)
и α
k
на каждой итерации характеризует особенности применяемого
метода. Например, поиск методом наискорейшего спуска (методом Коши)
сводится к построению
последовательности приближений {x
k
} по формуле
(2.6)
, где
()
()
()
()
,
()
k
k
k
fx
h
fx
∇
=−
∇
||∇f(x
(k)
)|| – длина вектора градиента ∇f(х
(k)
). Длина шага α
k
вычисляется путем
решения задачи одномерной минимизации
() ()
() ( ) min, ,
kk n
tfx th tϕ= + → ∈R
с помощью какого-нибудь из методов одномерной минимизации. Условием
окончания вычислительной процедуры является выполнение неравенства (2.7)
.
Метод наискорейшего спуска сходится быстрее, чем методы прямого
поиска. Однако скорость его сходимости при решении ряда практических за-
дач остается недопустимо низкой. Это вполне объяснимо, поскольку
cкорость изменения переменных непосредственно зависит от длины вектора
градиента ||∇f(x
(k)
)||, которая стремится к нулю, и отсутствует механизм уско-
рения движения к точке минимума на последних итерациях. Одно из главных
преимуществ этого метода связано с его устойчивостью. Метод обладает
важным свойством, которое заключается в том, что при достаточно малой
длине шага α
k
на всех итерациях выполняется неравенство f (x
(k
+
1)
) ≤ f(x
(k)
).
Благодаря этому свойству метод наискорейшего спуска, как правило, позво-
ляет существенно уменьшить значение целевой функции при движении из

ЛАБОРАТОРНАЯ РАБОТА 2. МЕТОДЫ БЕЗУСЛОВНОЙ ОПТИМИЗАЦИИ
Краткие теоретические сведения
Моделирование процессов и объектов в металлургии. Лаб. практикум
-33-
точек, расположенных далеко от точки минимума, и поэтому часто использу-
ется при реализации градиентных методов в качестве начальной процедуры.
Методы случайного поиска отличаются от регулярных методов оп-
тимизации намеренным введением элемента случайности. Они эффективны при
решении сложных задач больших размерностей с произвольно заданными це-
левыми функциями, когда регулярные методы, как правило, неприменимы.
Различают ненаправленный случайный поиск, направленный случай-
ный поиск без самообучения и с самообучением.
Ненаправленный случайный поиск (или метод статистических испыта-
ний, метод Монте-Карло) заключается в многократном моделировании не-
зависимых случайных вариантов решений из области допустимых, вычисле-
нии в каждом их них критерия оптимизации и запоминания наиближайшего к
экстремуму. Метод Монтe-Карло относится к числу универсальных, по-
скольку поз
воляет решать многоэкстремальные задачи общего вида с оты-
сканием глобальною экстремума. Основной недостаток
метода – необходи-
мость проведения большого числа испытаний для получения решения, доста-
точно близкого к оптимальному, т. е. наличие медленной сходимости к экс-
тремуму.
Обзор других методов безусловной оптимизации можно найти в лите-
ратуре [1
, 2, 3, 4, 5].
П
П
о
о
р
р
я
я
д
д
о
о
к
к
в
в
ы
ы
п
п
о
о
л
л
н
н
е
е
н
н
и
и
я
я
р
р
а
а
б
б
о
о
т
т
ы
ы
1.
Изучить основные понятия теории оптимизации, классификацию и
основные численные методы для решения задач оптимизации.
2.
В соответствии с индивидуальным заданием исследовать заданную
целевую функцию на экстремумы.
3.
Учитывая проведенное исследование, выполнить вычислительный
эксперимент в пакете прикладных программ MATHCAD.
4.
Сравнить полученные результаты.
5.
Оформить отчет, в который включить: титульный лист; формули-
ровку цели лабораторной работы; теоретическое описание используемого
численного метода и его сравнение с другими методами; геометрическую ин-
терпретацию метода; индивидуальное задание на работу; анализ полученных
результатов.
ЛАБОРАТОРНАЯ РАБОТА 2. МЕТОДЫ БЕЗУСЛОВНОЙ ОПТИМИЗАЦИИ
Порядок выполнения работы
Моделирование процессов и объектов в металлургии. Лаб. практикум
-34-
М
М
е
е
т
т
о
о
д
д
и
и
к
к
а
а
в
в
ы
ы
п
п
о
о
л
л
н
н
е
е
н
н
и
и
я
я
р
р
а
а
б
б
о
о
т
т
ы
ы
в
в
п
п
а
а
к
к
е
е
т
т
е
е
M
M
A
A
T
T
H
H
C
C
A
A
D
D
1. Получить задание.
2.
Запустить пакет MATHCAD.
3.
Ввести функцию в соответствии с вариантом задания.
4.
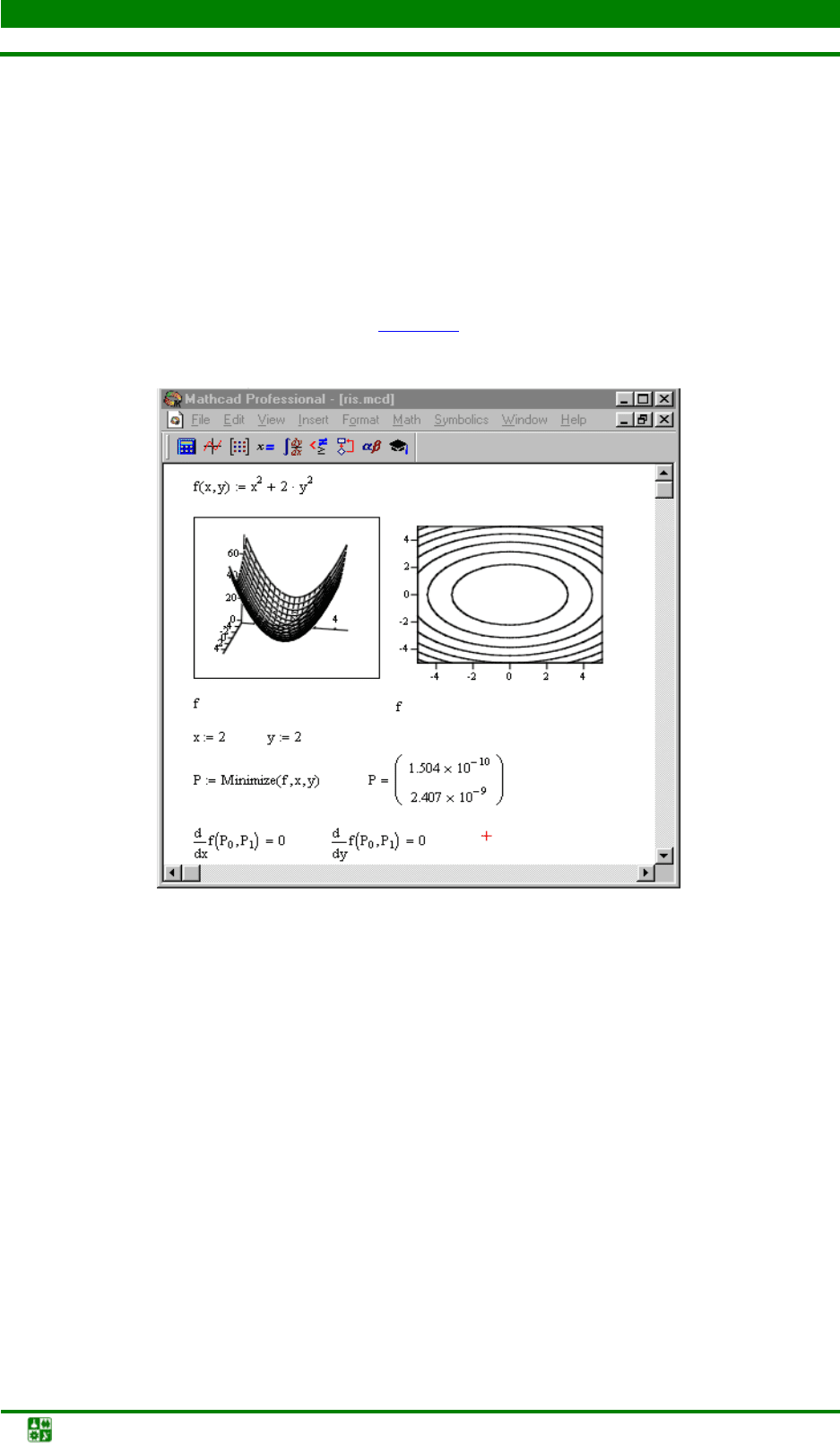
Построить график и линии уровня функции, используя компонент
Graph. Изменяя диапазоны значений переменных x, y, найти область, в кото-
рой линии уровня функции представляют собой замкнутые кривые, концен-
трически вложенные друг в друга (рис. 2.1
).
5.
Рис. 2.1. Пример решения задачи в пакете MathCad
6.
Решить задачу безусловной оптимизации. Для этого задать началь-
ные значения переменных в пределах найденной области и вычислить реше-
ние задачи с помощью встроенных функций
Maximize или Minimize.
7.
Проверить, удовлетворяет ли решение необходимым условиям оп-
тимальности.
8.
Распечатать результаты.
В пакете MATHCAD для решения задачи можно воспользоваться по-
мощью: Help → Solving and optimization → Maximizing or minimizing a function.

ЛАБОРАТОРНАЯ РАБОТА 2. МЕТОДЫ БЕЗУСЛОВНОЙ ОПТИМИЗАЦИИ
Моделирование процессов и объектов в металлургии. Лаб. практикум
-35-
З
З
а
а
д
д
а
а
н
н
и
и
е
е
Варианты индивидуальных заданий для выполнения работы в пакете
MathCad приведены в таблице:
Номер варианта Оптимизируемая функция
1
()
(
)
()
2
2
2
21 1
0,01 1
f
xxxx=⋅− +−
2
(
)
2
22
21 1
() 2 (1 )
f
xxx x=⋅ − +−
3
22
12
() 2 ( 1) ( 2)fx x x=+ − + −
4
22
1212
() 8 6 1fx x x xx=+ − +
5
22
112
() ( 1) 2( )
f
xx xx=−+⋅−
6
22
1212 1 2
() 3 6
f
xxxxx x x=++ −−
7
22
12 21
() 4( )
f
xxx xx=++⋅−
8
22
121212
() 1fx x x xx x x=++ +−+
9
22
12 12 1 2
() 6 39 18 20fx x x xx x x=+− − + +
10
22 2
1212
() ( 3) ( 2) ( 4)fx x x x x=−+−+−−
11
23
12 1 2
() 2 4 3 6fx x x x x=+−−+
12
22
1212 1 2
() 3 6
f
xxxxx x x=++ −−
13
() ( )
2
2
12 2
10 0,1
f
xxxx=⋅− +
14
22
12 12 1 2
() 4 2 2 8fx x x xx x x
=
+− − − +
15
3222
112 1 2
() 2 5
f
xxxxxx=−++
16
22
12 21
() 2 4( ) 6fx x x x x=++⋅−+
17
22
112212
() 8 4 2 4 4
f
xxxxxxx=+ ++−
18
22
12 1 2
()
f
xxxxx=++
19
22
12 12
() 2 2( 4 ) 5fx x x x x=+ +⋅+ +
20
22
12 121
() 5
f
xxx xxx=+− −

ЛАБОРАТОРНАЯ РАБОТА 2. МЕТОДЫ БЕЗУСЛОВНОЙ ОПТИМИЗАЦИИ
Моделирование процессов и объектов в металлургии. Лаб. практикум
-36-
К
К
о
о
н
н
т
т
р
р
о
о
л
л
ь
ь
н
н
ы
ы
е
е
в
в
о
о
п
п
р
р
о
о
с
с
ы
ы
и
и
з
з
а
а
д
д
а
а
н
н
и
и
я
я
1.
Дайте определения целевой и унимодальной функций?
2.
Что такое глобальный, локальный оптимум ?
3.
В чем заключается необходимое условие оптимальности в задаче
безусловной оптимизации?
4.
Сформулируйте достаточное условие оптимальности.
5.
Какие численные методы используются для оптимизации унимо-
дальных функций?
6.
Опишите основную идею методов исключения интервалов.
7.
В чем состоит суть метода Гаусса-Зейделя?
8.
Как задается направление убывания в градиентных методах?
9.
В чем заключается суть метода наискорейшего спуска?
10.
Чем определяется выбор метода оптимизации?

Моделирование процессов и объектов в металлургии. Лаб. практикум
-37-
Л
Л
А
А
Б
Б
О
О
Р
Р
А
А
Т
Т
О
О
Р
Р
Н
Н
А
А
Я
Я
Р
Р
А
А
Б
Б
О
О
Т
Т
А
А
3
3
П
П
Р
Р
И
И
М
М
Е
Е
Н
Н
Е
Е
Н
Н
И
И
Е
Е
М
М
Е
Е
Т
Т
О
О
Д
Д
О
О
В
В
Л
Л
И
И
Н
Н
Е
Е
Й
Й
Н
Н
О
О
Г
Г
О
О
П
П
Р
Р
О
О
Г
Г
Р
Р
А
А
М
М
М
М
И
И
Р
Р
О
О
В
В
А
А
Н
Н
И
И
Я
Я
Д
Д
Л
Л
Я
Я
М
М
О
О
Д
Д
Е
Е
Л
Л
И
И
Р
Р
О
О
В
В
А
А
Н
Н
И
И
Я
Я
И
И
Р
Р
Е
Е
Ш
Ш
Е
Е
Н
Н
И
И
Я
Я
П
П
Р
Р
О
О
И
И
З
З
В
В
О
О
Д
Д
С
С
Т
Т
В
В
Е
Е
Н
Н
Н
Н
Ы
Ы
Х
Х
З
З
А
А
Д
Д
А
А
Ч
Ч
Ц
Ц
е
е
л
л
ь
ь
р
р
а
а
б
б
о
о
т
т
ы
ы
Изучить теорию и методы решения задач линейного программирова-
ния; приобрести навыки построения моделей линейного программирования и
решения задач линейного программирования на ЭВМ.
К
К
р
р
а
а
т
т
к
к
и
и
е
е
т
т
е
е
о
о
р
р
е
е
т
т
и
и
ч
ч
е
е
с
с
к
к
и
и
е
е
с
с
в
в
е
е
д
д
е
е
н
н
и
и
я
я
Методы линейного программирования (ЛП) оказались весьма эффек-
тивными для решения задач из различных областей человеческой деятельно-
сти. Слово «программирование» понимается как планирование, и это опреде-
ляет характер рассматриваемых приложений. Основные идеи линейного про-
граммирования возникли во время Второй мировой войны в связи с поиском
оптимальных стратегий при ведении военных операций. С тех пор он
и нашли
широкое применение в промышленности, торговле и в управлении как в мест-
ных, так и в государственных масштабах. Этими методами можно решить мно-
гие задачи, связанные с эффективным использованием ограниченных ресурсов.
П
П
р
р
и
и
м
м
е
е
р
р
д
д
в
в
у
у
м
м
е
е
р
р
н
н
о
о
й
й
з
з
а
а
д
д
а
а
ч
ч
и
и
л
л
и
и
н
н
е
е
й
й
н
н
о
о
г
г
о
о
п
п
р
р
о
о
г
г
р
р
а
а
м
м
м
м
и
и
р
р
о
о
в
в
а
а
н
н
и
и
я
я
Фирма производит две модели (А и В) сборных книжных полок. Их
производство ограничено наличием сырья (высококачественных досок) и
временем машинной обработки. Для каждого изделия модели А требуется
3 м
2
досок, а для изделия модели В – 4 м
2
. Фирма может получить от своих
поставщиков до 1 700 м
2
досок в неделю. Для каждого изделия модели А тре-
буется 12 мин машинного времени, а для изделия модели В – 30 мин. В неде-
лю можно использовать 160 ч машинного времени.
Сколько изделий каждой модели следует фирме выпускать в неделю,
если каждое изделие модели А приносит 2 дол. прибыли, а каждое изделие
модели В – 4 дол. прибыли?
Чтобы сформулировать эту задачу математически, обозначим через
x
1
количество выпущенных за неделю полок модели A, а через x
2
– количе-
ство выпущенных полок модели В. Задача состоит в том, чтобы найти наи-
лучшие значения x
1
и x
2
. Очевидно, наилучшими для данной задачи являются

ЛАБ. Р. 3. ПРИМЕНЕНИЕ МЕТОДОВ ЛИНЕЙНОГО ПРОГР-Я ДЛЯ МОДЕЛИРОВАНИЯ И РЕШ-Я ПРОИЗВОДСТВЕННЫХ З
А
Д
АЧ
Краткие теоретические сведения
Моделирование процессов и объектов в металлургии. Лаб. практикум
-38-
такие значения, которые максимизируют еженедельную прибыль. Ежене-
дельная прибыль составляет Р = 2x
1
+ 4x
2
.
Поскольку x и x
2
выражают еженедельный объем выпускаемых изде-
лий, то они не могут быть отрицательны, т.е.
x
1
≥ 0, x
2
≥ 0. (3.1)
Теперь ограничения на наличие досок и машинное время могут быть
записаны следующим образом:
для досок –
3
x
1
+ 4x
2
≤
1 700, (3.2)
для машинного времени –
2x
1
+ 5x
2
≤
1 600. (3.3)
Следовательно, задача состоит в том, чтобы найти значения x
1
и x
2
,
удовлетворяющие условиям неотрицательности (3.1)
и ограничениям типа
неравенства (3.2)
, (3.3) и максимизирующие функцию Р.
Это типичная двумерная задача линейного программирования. Целе-
вая функция, которая должна быть максимизирована, является линейной
функцией своих переменных. Ограничения на эти переменные тоже линейны
(рис. 3.1
).
Условия неотрицательности позволяют ограничиться рассмотрением
положительного квадранта. Границы определяются прямыми
3x
1
+ 4x
2
= 1 700,
2x
1
+ 5x
2
= 1 600.

ЛАБ. Р. 3. ПРИМЕНЕНИЕ МЕТОДОВ ЛИНЕЙНОГО ПРОГР-Я ДЛЯ МОДЕЛИРОВАНИЯ И РЕШ-Я ПРОИЗВОДСТВЕННЫХ З
А
Д
АЧ
Краткие теоретические сведения
Моделирование процессов и объектов в металлургии. Лаб. практикум
-39-
Рис. 3.1. Геометрическая интерпретация задачи ЛП
Стрелка на каждой границе указывает, с какой стороны прямой вы-
полняется ограничение. Заштрихованная область OАВС, содержащая точки,
для которых соблюдены условия (3.2)
и (3.3), является допустимой. Задача
состоит в том, чтобы найти точку максимума функции Р.
Штриховыми линиями изображены две линии уровня функции Р со
значениями, соответственно, 0 и 800, обозначенные a и b. Ясно, что значение
функции Р возрастает по мере того, как линии уровня удаляются от начала
координат в положительном квадранте. Действительно, вектор градиента
12
grad ,
PP
P
x
x
⎛⎞
∂∂
=
⎜⎟
∂∂
⎝⎠
, т.е. вектор с компонентами (2, 4), указывающий направ-
ление возрастания функции Р, перпендикулярен линиям уровня и направлен
в сторону, противоположную началу координат.
Линией уровня с наибольшим значением функции Р, имеющей хотя
бы одну точку с допустимой областью, является прямая c, проходящая через
вершину В; на ней Р принимает значение 1 400.
Точка В, в которой x
1
= 300,
x
2
= 200, соответствует оптимальному решению задачи. На данном примере
показано, как возникают задачи линейного программирования на практике и
как их можно решить, используя графический метод.
Рассмотренная задача может быть расширена до трех и более ограни-
чений и соответствующего количества неотрицательных переменных. Могут
быть введены дополнительные ограничения, связанные с возможностями
рынка, упаковкой и т.д. В этом случае зад
ача по-прежнему заключается в
максимизации линейной функции от нескольких переменных при линейных
ограничениях.

ЛАБ. Р. 3. ПРИМЕНЕНИЕ МЕТОДОВ ЛИНЕЙНОГО ПРОГР-Я ДЛЯ МОДЕЛИРОВАНИЯ И РЕШ-Я ПРОИЗВОДСТВЕННЫХ З
А
Д
АЧ
Краткие теоретические сведения
Моделирование процессов и объектов в металлургии. Лаб. практикум
-40-
О
О
б
б
щ
щ
а
а
я
я
з
з
а
а
д
д
а
а
ч
ч
а
а
л
л
и
и
н
н
е
е
й
й
н
н
о
о
г
г
о
о
п
п
р
р
о
о
г
г
р
р
а
а
м
м
м
м
и
и
р
р
о
о
в
в
а
а
н
н
и
и
я
я
Задача линейного программирования (ЗЛП) в общей постановке со-
стоит в отыскании точек минимума или максимума линейной функции
z = c
1
x
1
+ c
2
x
2
+ . . . + c
n
x
n
от n вещественных переменных x
1
, x
2
, …, x
n
на допустимом множестве Х ⊂ R
n
точек, удовлетворяющих условиям
a
11
x
1
+ a
12
x
2
+ ... + a
1n
x
n
≥ b
1
,
a
21
x
1
+ a
22
x
2
+ ... + a
2 n
x
n
≥ b
2
,
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . (3.4)
a
l1
x
1
+ a
l 2
x
2
+ ... + a
l n
x
n
≥ b
l
,
a
l +1,1
x
1
+ a
l +1,2
x
2
+ ... + a
l +1,n
x
n
= b
l+1
,
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
a
m1
x
1
+ a
m 2
x
2
+ ... + a
m n
x
n
= b
m
(m ≥ l),
и условиям неотрицательности
12
0, 0, , 0 (1 ).
k
ss s
x
xx kn≥≥ ≥≤≤… (3.5)
Значения b
i
,
c
j
, a
ij
предполагаются известными. Каждая точка допус-
тимого множества X называется допустимой точкой или допустимым ре-
шением.
К
К
а
а
н
н
о
о
н
н
и
и
ч
ч
е
е
с
с
к
к
а
а
я
я
з
з
а
а
д
д
а
а
ч
ч
а
а
л
л
и
и
н
н
е
е
й
й
н
н
о
о
г
г
о
о
п
п
р
р
о
о
г
г
р
р
а
а
м
м
м
м
и
и
р
р
о
о
в
в
а
а
н
н
и
и
я
я
Все
задачи линейного программирования могут быть приведены к так
называемой канонической форме, в которой целевая функция должна быть
минимизирована, а все ограничения должны быть заданы в виде равенств с
неотрицательными переменными.
Задача линейного программирования в канонической форме записы-
вается следующим образом: минимизировать функцию
z = c
1
x
1
+ c
2
x
2
+ . . . + c
n
x
n
(3.6)
при ограничениях
