Lyons W.C. (ed.). Standard handbook of petroleum and natural gas engineering.2001- Volume 1
Подождите немного. Документ загружается.


Chemistry
355
Check: Using heats of combustion data,
(i)
AH:
=
AH:(C,H,,)-
AH:(C,H,)- AH:(C,H,)
=
(-687.982)
-
(-337.234)
-
(-372.820)
=
+22.072 kcal for first reaction
(ii)
AH;
=
AH;(co,)+AH:(H,)-AH:(co)-AH:(H,o)
=
0
-
68.317
-
(-67.636)
-
0
=
-0.681 kcal for second reaction
Thus, both methods yield identical results for the heats of reaction.
(3)
Very frequently AH: data are available for inorganic substances but not for
organic compounds for which AH: values are more readily available. Because AH:
of hydrocarbons are not easily measurable, they are often deduced by Hess's law
from known AH:
of
the hydrocarbon and known AH: values
of
the products
of combustion.
Example
2-44
Find the standard heat of formation of benzene
(I)
given the following heats
of
combustion data (in kcal/gmole) at 1 atm and 25OC:
Solution
The desired formation reaction is
6C(c)
+
3H,(g)
+
C,H,(P)
AH:
=
?
which is equivalent
to
[6
Equation (i)
+
3 Equation (ii)
-
Equation (iii)].
By Hess' law,
AH;
=
C
~,AH,D,~
-
C
V~AH;,,
R
P
=
6(-94.05)
+
3(-68.32)
-
1(-780.98)
=
-564.30
-
204.96
+
780.98
=
11.72
kcal/g-mole
Effect
of
Temperature
on
the Heat
of
Reaction.
It is possible to calculate the heat
of
a chemical reaction AHAT,) at any temperature T, and pressure
P,
provided we
know the standard heat of reaction
AH:
(T,)
at reference conditions of T,
and
P
(e.g.,
25°C and
1
atm).
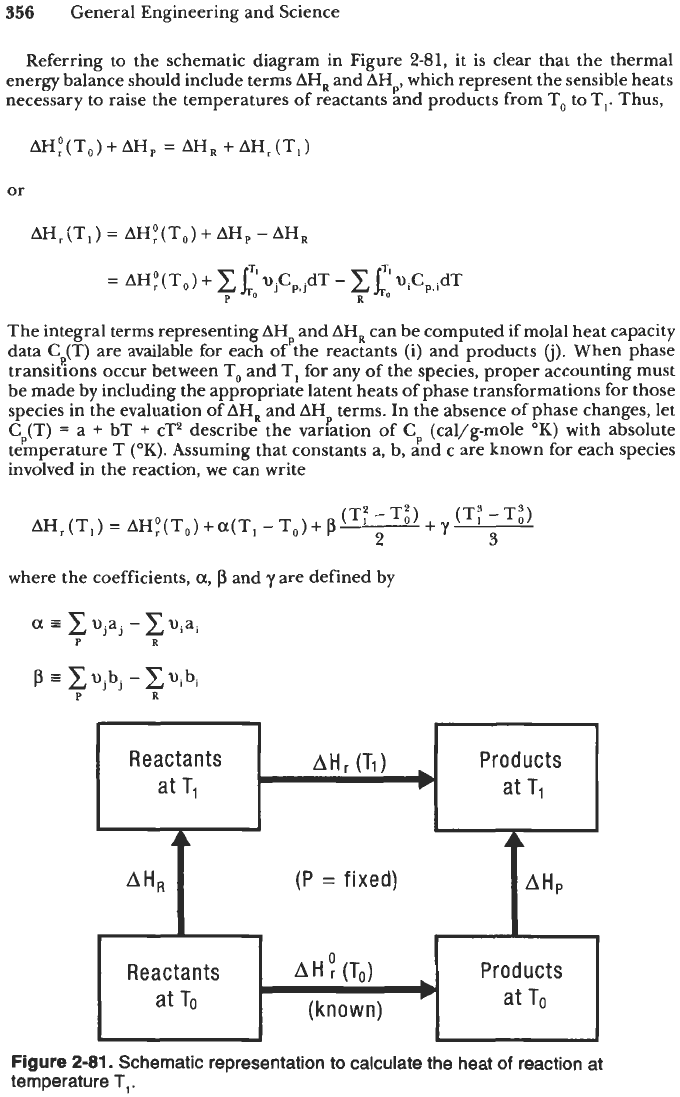
356
General Engineering and Science
Reactants
at
T,
Referring to the schematic diagram in Figure
2-81,
it is clear that the thermal
energy balance should include terms
AHR
and AHp, which represent the sensible heats
necessary to raise the temperatures of reactants and products from To
to
T,. Thus,
AHr
(Tl)
Products
at
T1
AH;(T,)+AH,
=
AH^
+AH,(T,)
AH,
or
(P
=
fixed)
AHP
AH,(T,)
=
AH;(T,)
+
AH^
AH^
Reactants
at
To
The integral terms representing AHp and AHR can be computed
if
molal heat capacity
data CJT) are available for each of the reactants (i) and products
6).
When phase
transitions occur between To and
T,
for any
of
the species, proper accounting must
be made by including the appropriate latent heats of phase transformations for those
species in the evaluation of AHR and AH,, terms. In the absence of phase changes, let
Cp(T)
=
a
+
bT
+ cT2
describe the variation
of
Cp
(cal/g-mole
OK)
with absolute
temperature T
(OK).
Assuming that constants a, b, and c
are
known for each species
involved in the reaction, we can write
AH
(TO)
Products
I
b
(known)
at
To
where the coefficients,
a,
p
and
y
are defined by
a
=
Cujaj
-
Cviai
P
R
fi
=
vjbj
-
uibi
P
R

Chemistry
357
TI'C)
2.5
100
200
300
400
500
600
700
900
1000
I100
1200
1400
1500
1700
800
1300
i6on
i8no
i9no
20ooo
2100
5200
In
a
more compact notation, the same result becomes
HP
6.894
6.924
6.957
6.970
6.982
6.905
7.011
7.032
7.076
7.128
i.169
7.209
7.288
7.326
7.421
i.n6o
7.252
7.m
7.467
7.505
7.948
7.S88
i.624
PT:
fl;
AH,(T,)= H,,+aT,+-+-
23
8.024
8.084
8.213
8.177
8.409
8.539
8.678
8.963
9.109
9.246
9x4
9.66
9.77
9.89
9.95
8.816
9.389
0.13
0.24
0.34
0.43
0.52
0.61
where
COP
8.88
9.2.5
10.10
9.70
1046
10.77
11.05
11..53
11.74
11.92
12.25
12.39
12.io
12.69
12.7.5
ii.30
mri
12.70
12.93
13.01
13.10
13.li
13.24
is a function
of
To only.
Sometimes tabulated values of the
mean
molal
heat
capacities
cp
(T) are more easily
accessible than
C,(T_,
data, with respect to a reference temperature
of
T,
=
25°C
(see
Table
2-45).
Since
C,
is
defined over the range
T,
and TI by
S%
9.94
9.85
10.25
10.62
10.94
11.22
11.45
11.66
11.84
12.01
12.15
12.ZH
12.39
1
irr'
C,
(T)dT
-
c,
=
(TI
-Tn)
'I
CP%
so3
CnH6
10.43 12.11
12.63
11.35 12.84 1576
12.53
I3.i-l
I3.Z
13.6.5
14.54
lii.72
14.67 iw:!
IR.II
15.60
15.82 19
3Y
16.45
16.33
20.58
17.22
lki7
21
68
17.95 l7.li
22.72
18.63 17.32
23
IiO
19.23
17.80
21
iii
1981 18.17
25.41)
20.38
18.44
2fi.l.i
we can rewrite the expression for
AH,(T,)
as
Table
2-45
Mean Molal Heat Capacities of Gases Between 25°C and T"C
(Reference pressure
=
0)
(cal/(g-mole)(%))
[61,
p.
2581
6.961
6.972
6.996
7.036
7.080
7.
I59
7.229
7.298
7.369
7.443
7.307
7.574
7.635
7.692
7.738
7.786
7.844
7.879
7.924
7.957
7.994
8.028
8.054
-
co
6.965
6.983
7.017
7.070
7.196
i.2in
7.289
7.365
7.445
7.521
7.587
7.653
7.714
7.772
7.815
7.866
7.922
7.958
8.001
8.035
8.069
8.101
8.127
-
Air
6.972
6.996
7.021
7.073
7.132
7.225
7.299
7.374
7.447
1.320
1.393
7.660
7
719
7.778
7.824
i.373
7.929
7.965
-
.'
+._
8.ow
8.043
8.081
8.115
3.144
_.
02
7.01i
7.089
7.181
7.293
7.406
7.513
7.616
7
706
7.792
7.874
7.941
8.009
8.06X
8.1?3
8.166
8.203
8.760
8.305
8.349
8.383
8.423
8.460
8.491
-
NO
7.194
7.144
7.224
7.252
i.m
7.389
7
470
7.349
7.630
7.708
7.773
7.839
7.898
7
952
7.994
8.059
8.124
8.164
8.192
8.225
3.255
8.277
8.092
-
HC
I
6.96
5.97
5.98
7.00
7.02
7.06
7.1.5
7.21
7.27
7.33
7.39
7.4.5
-
7.10
-
-
UP
8.12
8.24
8.37
8.48
8.55
8.61
8.66
8.70
8.73
8.77
8.80
8.82
8.94
-
-
-
MI
8.53
8.98
9.62
0.29
0.97
1.6.5
2.27
2.90
3.48
4.04
4.56
5.04
3,49
-

358
General Engineering and Science
In the event the mean molal heat capacity data
are
available with a reference
temperature T, other than
To
=
25°C
(see Table
2-46
for data with Tr
=
OOC),
the
following equation can be used to calculate
AHr(Tl):
AHr
(
T,
)
=
AH:
(
T,
)
+
(
T,
-
T,
)A
-
(T,
-
T,
B
where
A,
B
=
u~E,,~
-
u~C,,~
P
R
excepting that the mean heat capacities are evaluated between
Tr
and
TI
for term
A
and between
T,
and
T,
for
term
B.
Effect
of
Pressure on
Allr,
Consider a reaction carried out at reference temperature
T
=
25°C
but at a constant pressure
P,
different from the initial standard-state pressure
Po
=
1
atm. The value of
AHr
(PI)
can be found from an energy balance similar to the
previous analysis:
AHr
(PI
)
=
AH:(
Po)
+
AHp
-
AHR
The terms
AHp
and
AHR
now denote the enthalpy changes associated with the change
of pressure from
Po
to
P,.
Thus
Table 2-46
Mean Molal Heat Capacities
of
Combustion Gases Between 0°C and f°C
(Reference temperature
=
0°C; pressure
=
1
atm) [60, p.
2731
(E,,
in cal/(gm-mole)(°C)
(To convert
to
J/kg mole)("K), multiply by 4184.)
T('C)
Nz
02
Air
H2
co
co2
HzO
0
6.959
6.989
6.946 6.838
6.960
8.595 8.001
18
6.960 6.998
6.949
6.858
6.961
8.706 8.009
25
6.960
7.002
6.949
6.864
6.962
8.716 8.012
1
00
6.965
7.057
6.965 6.926
6.973
9.122 8.061
200
6.985
7.154
7.001
6.955
7.050
9.590 8.150
300
7.023
7.275
7.054 6.967
7.057
10.003 8.256
400
7.075
7.380
7.118
6.983
7.120
10.360 8.377
500
7.138 7.489
7.190
6.998 7.196
10.680 8.507
600
7.207 7.591
7.266
7.015 7.273
10.965 8.644
700
7.277
7.684
7.340
7.036
7.351
11.221 8,785
800
7.350 7.768
7.414
7.062
7.428
11.451 8.928
900
7.420
7.845
7.485
7.093
7.501
11.68
9.070
IO00
7.482 7.916
7.549 7.128
7.570
11.85 9.2
IO
1100
7.551 7.980
7.616
7.165
7.635
12.02 9.348
1200
7.610 8.039
7.674 7.205
7.688
12.17 9.482
1300
7.665 8.094
7.729
7.227
7.752
12.32 9.613
I400
7.718 8.146
7.781 7.260
7.805
12.44 9.740
1500
7.769 8.192
7.830
7.296
7.855
12.56 9.86

Chemistry
359
where d/aP denotes partial differentiation with respect to pressure P. For solids and
liquids away from the critical point, the variation in enthalpy with pressure at constant
T is quite small and, therefore, AH,(P,) AH:(P,)is assumed under these circum-
stances. For gaseous reactants and products that follow ideal-gas law, H
=
H(T) only
so
that the effect of pressure is zero, i.e.,
AH,(P,)
=
AH:(P,). In nonideal gas systems,
the enthalpy changes are nonzero, but the effect is usually small up to moderate pressures.
Heating Values
Of
Combustion Fuels.
The calorific value or heating value (HV) of
a fuel (usually a hydrocarbon) is the negative value of its standard heat of combustion
at
1
atm and 25"C, expressed in cal/g or Btu/lb. It is termed
higher heating value
(HHV)
if
H,O(Q is a combustion product and is calculated as HHV
=
(-AH:)/M,
where
M
is the molecular weight of the fuel. An appropriate
AH;
value must be used
in referring to the
lower
heating value
(LHV) based on H,O(g) as a combustion product.
Both are related by
HHV=LHV+(v,kJ/M
where
U,
is the stoichiometric coefficient for water in the combustion reaction
of
1
mole of fuel, and
kV
is the molal latent heat of vaporization for water at 25°C
and
1
atm
=
10,519
cal/g-mole
=
18,934
Btu/lb-mole.
For a fuel mixture composed of combustible substances
i
=
1,
2,
.
,
.
,
the heating
value is calculated as HV
=
&o~(HV)~, where
ai
is the mass fraction of the ith substance
having a heating value of (HV),.
Adiabatic Reaction Temperature
(Tad).
The concept of adiabatic or theoretical
reaction temperature (T,) plays an important role in the design of chemical reactors,
gas furnaces, and other process equipment to handle highly exothermic reactions
such as combustion. Tad is defined as the final temperature attained by the reaction
mixture at the completion of a chemical reaction carried out under adiabatic
conditions in a closed system at constant pressure. Theoretically, this is the maximum
temperature achieved by the products when stoichiometric quantities of reactants
are completely converted into products
in
an adiabatic reactor. In general,
Tad
is
a
function of the initial temperature
(Ti)
of the reactants and their relative amounts as
well as the presence of any nonreactive (inert) materials. Tad is also dependent on the
extent of completion of the reaction. In actual experiments, it is very unlikely that
the theoretical maximum values of Tul can be realized, but the calculated results do
provide an idealized basis for comparison
of
the thermal effects resulting from
exothermic reactions. Lower feed temperatures
(Ti),
presence of inerts and excess
reactants, and incomplete conversion tend to reduce the value of T,. The term
theoreticaz
or
adiabatic flume temperature
(TJ
is
preferred over Tad in dealing exclusively
with the combustion of fuels.
Calculation
of
Td.
To
calculate
Tad
(or T,, for a combustible fuel),
we
refer to
Figure 2-82 and note that
Q
=
AH
=
0
for the adiabatic reaction process. Taking
25°C
(=
298.2"K) and
1
atm as the reference state, the energy balance can be
expressed as
=
-AHR +AH:(25"C)+AHp

360
General Engineering and Science
-
AHR
(P
=
fixed)
AHP
Figure
2-82.
Schematic representation
to
calculate the adiabatic reaction
temperature
(Tad).
or
Reactants
at
25°C
mP
=
-AH;
+
mR
AH:
Products
at
25°C
(known)
where
AH,
=
xJ2niC,,,dT
R
and
AHp
=
cnjC,,jdT
+
x
njh,,j
P P
The second term on the right side of the expression for
AH
accounts for
any
phase
changes that may occur between
25OC
and Tad for the fina! products; it should be
deleted if not applicable. Using molal heat capacity data CAT)
for
all the species
present, the following equality is solved for Tad by trial and error.
For
instance, a quadratic expression for
CAT)
will require the solution of a cubic
equation in
Tad.

Chemistry
361
-
An alternative representation is useful when data on mean molal heat capacities
Cp(T) are available with
25°C
as the reference temperature
(T,,).
Then the equation
can be solved for
Tad,
though it still requires a trial-and-error procedure.
Example
245
A
natural gas having the volumetric composition of
90%
methane,
8%
ethane, and
2%
nitrogen at
1
atm and
25°C
is used as fuel in a power plant.
To
ensure complete
combustion
75%
excess air
is
also supplied at
1
atm and 25°C. Calculate (i) the lower and
higher heating values of the fuel at
25°C
and (ii) the theoretical maximum temperature
in the boiler assuming adiabatic operation and gaseous state for all the products.
Solution
Assuming ideal gas behavior at
1
atm and
25"C,
the volume composition is
identical with the mole composition. Choose a
basis
of 1 g-mole of natural gas (at
1
atm and
25°C)
which contains
0.90
g-mole
of
CH,
(MW
=
16.04), 0.08
g-mole of
C,H, (MW
=
30.07),
and
0.02
g-moles of
N,
(MW
=
28.01).
Then the molecular
weight of the natural gas is
M
=
yiM,
=
0.90(
16.04)
+
0.08(30.07)
+
0.02 (28.01)
=
17.40
g/g-mole
(i)
The combustion reactions of interest are
CH,(g)+PO,(g)
+
CO,(g)+2H,O(t)
7
2
C,H,(g)
+
-O,(g)
-+
2CO,(g)
+
3H,O(t)
where the standard heat of combustion Ah:
iz-mole.
AH::
=
-212.80
AH::
=
-372.82
at 1 atm and
25°C
are stated in kcal/
0
With H,0(4) as a product, the higher heating value
(HHV)
of the fuel is calculated as
HHV
=
0.9[
-
AH
::
(CH
)]
+
0.08[
-
AH
::
(C,H
)]
=
0.9(212.80)
+
0.08(372.82)
=
221.35
kcal/g-mole
-
221. '35
-
-
=
12.72
kcal/g
17.40
Note that H,O(P)
+
H,O(g)
at
1
atm and
25°C
has
h,
=
AH:
=
10.519kcal/g-mole.
With
H20(g)
as a combustion product,
the
lower heating value
(LHV)
of
the fuel is

362
General Engineering and Science
LHV=HHV- nwhv
=
221.35
-
[0.9(2)
+
0.08(3)](10.519) kcal/g-mole
=
199.89 kcal/g-mole
=
11.49 kcal/g
(ii) The adiabatic flame temperature Tf, must be calculated with all products in the
gaseous state.
So
the appropriate standard heat of reaction at
1
atm and 25°C is the
heat of combustion of the fuel with H,O(g) as a product, i.e., the negative of LHV.
:.
AH:
=
-(
LHV
)
=
-199.89 kcal/g-mole
Stoichiometric amount of
0,
required
=
2( 0.9)
+
-
(0.08)
7
2
=
2.08 g-moles
Because 75% excess
air
is
supplied, amount
of
0,
supplied
=
1.75(2.08)
=
3.64 g-moles.
(3.64)(0.79)/0.21
=
13.693 g-moles.
products leaving the boiler at T,,
are
tabulated below:
Assuming dry air to contain 79%
N,
and 21%
0,
by moles,
N,
supplied
=
The mole compositions of the feed gases entering (reactants i) at 25°C and of the
Feed at
25°C
Products at
T,,
Gas
i
n,
(g-moles)
Gas
j
n,
(9-moles)
0.9(1)
+
0.08(2)
=
1.06
0.08
H,O
0.9(2)
+
0.08(3)
=
2.04
0.90
CO,
CH,
C,H,
N*
N,
in
air
Stoich.
0,
2.08
Excess
0,
1.56
0,
}
3.64
Total
18.333
0.02
13.693
}
13.713
N,
13.373
1.56
Total
18.373
Applying the heat balance equation,
AH
=
0
=
AH:
-
AH,
+
AHp,
we
realize
that AHR
=
0
because the feed gases are supplied at the reference temperature
of
25%
=
298°K.
:.
AHp
=
~~~8n,C,,jdT
=
-AH:
=
+199,890 cal
P
must be solved for unknown Tf,.
Method
1.
Use
C
(T) data for product gases from Himmelblau
[60,
pp.
494-4971,
The equation is
c",
=
a
+
bT
+
cT2, with T in
OK
and
Cp
in cal/g-mole
OK.

Chemistry
363
Gas
a
b
x
lo2
c
x
lo5
Applicable
range
("K)
CO&)
6.393 1.0100 -0.3405 273-3700
H,O(g)
6.970 0.3464 -0.0483
NSg)
6.529
0.1488 -0.02271 273-3700
O,(g)
6.732
0.1505
-0,01791 273-3700
The equation
for
T,,
now becomes
199,890=
a(T,
-298)+-(T;
P
-298*)+-(T:
Y
-2983)
2
3
where
a
=
zn,ia,i
P
=
1.06(6.393)+2.04(6.970)+
13.713(6.529)+1.56(6.732)
=
6.777+14.219+89.532+10.502
=
121.029
Similar calculations yield
P
=
xnibj
=
4.053~
lo-'
P
and
y
=
xn,c,
=
-0.799~10-~
f'
A
trial-and-error procedure is needed to solve the cubic equation in Tf,:
199,890
=
121.029(T, -298)+2.027xlO-'(T~ -298')
-0.266~10-~(Ti, -298")
As
a
first trial let
T,,
=
1,500"C
=
1773°K.
Then
RHS
=
178,518
+
61,909
-
14,774
=
225,652
cal (too high)
Try
T,,
=
1,400"C
=
1,673"K
as a second trial value. Then
RHS
=
166,415
+
54,925
-
12,402
=
206,566
(high)
Similar calculations show that with T,,
=
1345°C
=
1618"K,
the
RHS
=
159,759
+
51,257
-
11,212
=
199,804
which is very close
to
LHS
=
199,890
:.
The
solution
is
T,,
1345" C.
Method
2.
Use
mean heat capacity data from Table
2-45
with reference conditions of
P
=
0
and
T
=
25°C
for
the combustion gases. Then the equation for T,, becomes

364
General Engineering and Science
199,890
=
xnjcp,j(Tn
-
25)
P
=
[1.06~p(C0,)+2.04~p(H,0)+13.713~p(N,)+
1.56Cp(0,)]
x
(T,
-
25)
With
a
first trial value of T,,
=
1400°C,
we have
RHS
=
[1.06(12.50)
+
2.04(9.77)
+
13.713(7.738)
+
1.56(8.166)](1400
-
25)
=
(152.031)(1375)
=
209,043
cal
(high)
For the second trial, try
T,,
=
1350°C.
Then
RHS
=
[1.06(12.445)
+
2.04(9.715)
+
13.713(7.715)
+
1.56(8.145)](1325)
=
200,754
cal.
which is nearer to the LHS. Thus, using interpolated values
of
E,
between the
temperatures
1300°C
and
1400"C,
we find good agreement between
RHS
=
199,927
and LHS
=
199,890
at
T,,
=
1345°C.
Method
3.
Use mean molal heat capacity data from Table
2-46
with reference
conditions of
0°C
and
1
atm. Then the equation for T,, is
199,890
=
xnjcp,.j(T,
-O)-xnjcp,j(25-0)
P
P
or
njcp,jT,
=
199,890+
[1.06(8.716)+2.04(8.012)+
13.713(6.960)+ 1.56(7.002)](25)
P
=
199,890
+
3,299
=
203,189
cal
which can be written as
203,189
=
[1.06Ep(C0,)
+
2.04cp(
H,O)
+
13.713Ep(N,)
+
1.56cp(0,)]T,
Again, assume a trial value of
T,,
=
1400°C
for
which
RHS
=
[1.06(12.44)
+
2.04(9.74)
+
13.713(7.718)
+
1.56(8.146)](1400)
=
212,240
(high)
The results obtained with other trial values are shown below:
2nd
trial:
T,,
=
1350°C
3rd trial:
T,,
=
1345°C
RHS
=
203,855
RHS
=
203,034
