Lyons W.C. (ed.). Standard handbook of petroleum and natural gas engineering.2001- Volume 1
Подождите немного. Документ загружается.


Chemistry
335
circumstances, the reaction mixture at the conclusion of the process will include the
products together with some
of
the unreacted reactants present in excess of their
stoichiometric requirements. By identifying a limiting reactant, the
percent excess
is
calculated for any
excess reactant
as
100
(n
-
n*)
%
excess
=
~
n*
where
n
is number of available moles
of
excess reactant, and n* is theoretical (i.e.,
stoichiometric) moles required to react with the limiting reactant.
Conversion
(or degree of conversion) refers
to
the fraction of the feed or fraction
of
some reactant in the feed which has been converted into products.
The
degree
of
completion
of
a reaction refers to the fraction
of
the limiting reactant
that has been converted into products.
When a single reactant is converted into a single product, the
yield
for the reaction
is expressed as the ratio
of
the moles (or mass)
of
the product formed to the moles
(or mass) of the initial reactant.
In processes involving the combustion of fuels, either pure oxygen or air is supplied
in amounts greater than the stoichiometric requirements for complete combustion.
The terms “theoretical air” or “theoretical oxygen” are thus frequently encountered
in combustion problems. The molar composition of dry air at atmospheric
conditions [from
International Critical Tables,
Volume
1,
p.
393 (1926)l:
Mole%
Nitrogen 78.03
Oxygen
20.99
Argon
0.94
Carbon dioxide 0.03
0.01
100.00
H,,
He, Ne,
Kr,
Xe
Average molecular weight
=
28.97
For
combustion calculations,
it is acceptable to take the average molecular weight
of dry air to be
28.97,
and to
assume
a simplified composition of
79.0
mole%
nitrogen and
21.0
mole% oxygen (or equivalently,
76.8
wt% nitrogen and
23.2
wt%
oxygen).
In summary, the procedure to be adopted in material balance calculations involving
reactive systems is as follows:
1.
Identify the system and the process.
2.
Examine the stoichiometry of the chemical reaction, and identify the limiting
reactant and excess reactants.
3.
Choose a basis of calculations.
4.
Perform an overall material balance and the necessary component material
balances
so
as
to
provide the maximum number of independent equations. In
the event the balance is written in differential form, appropriate integration
must be carried out over time, and the set of equations solved for the unknowns.
For a nonreactive system, the material balance may be done either on a mass or on
a molar basis.

336
General Engineering and Science
Example
2-36
Consider the combustion
of
ethane (C,H,) in pure oxygen.
If
100 lb
of
ethane are
available and 10% excess oxygen is supplied to ensure complete combustion, calculate
(1)
the amount of oxygen supplied, and
(2)
compositions
of
the reactants and products
on mass and molal bases.
Solution
Choose
a
basis
of
100
lb of ethane (limiting reactant). The stoichiometric equation is
C,H,
+
(9)
0,
d
2C0,
+
3H,O
k
I
2
3
lb-moles
-
vi
=
1
2
Mi
=
30.07 32.00 44.01 18.01 lb/lb-moles
Thus,
1
mole of ethane reacts with
4
moles
of
0,
to produce
2
moles of CO,
and
3
moles
of
H,O vapor.
lb-moles
of
C,H, available
=
100/30.07
=
3.326
Stoichiometric lb-moles
of
0,
required
=
(
-)(3.326)
=
11.640
With
10%
excess, lb-moles of
0,
supplied
=
1.1
(11.64)
=
12.804
1.
Amount
of
0,
supplied
=
12.804(32.00)
=
409.71 lb
2.
Calculation
of
the composition of the feed (reactant) mixture is shown below.
7
2
Mass
m,
n,
Reactant
i
(Ib)
Weight
%
(1
b-moles)
Mole
%
Ethane
100.00
24.41
3.326 20.49
Oxygen
409.71
75.59 12.804 79.51
Total
509.71 100.00
16.230 100.00
In the product mixture, amount
of
excess (unreacted)
0,
=
O.l(l1.64)
=
1.164
lb-moles
=
37.25
lb.
Amount of CO, formed
=
(2)(100)/30.07
=
6.651 lb-moles
=
292.72 lb
Amount
of
H,O
formed
=
(3)(100)/30.07
=
9.977 lb-moles
=
179.73 lb
Hence, the composition
of
the product gas stream can be calculated as follows:
Mole
%
"1
Mass
ml
292.72 57.43 (88.71) 6.651 37.38
(85.11)
37.25 a(11.29) 1.164 6.54 (14.89)
Product
j
(Ib)
Weight
%
(Ib-moles)
179.73 35.26
(-)
9.977 56.08
(-)
CO,
HZO
02
Total
509.70 100.00 17.792 100.00

Chemistry
337
The values in parentheses show the product composition on a dry basis, excluding
H,O
vapor.
Ideal Gas Behavior
Ideal (or perfect) gas behavior is approached by most vapors and gases in the limit
of low pressures and elevated temperatures. Two special forms of restricted utility
known as the Boyle’s law and the Charles’ law preceded the development of the
perfect gas law.
Boyle’s Law.
At constant temperature (T), the volume (V)
of
a fixed mass of an ideal
gas is inversely proportional to the absolute pressure (P). That
is,
V=- or PV
=
constant (T
=
constant)
P
Charles’ Law.
At constant pressure (P), the volume (V) of a given mass
of
an ideal
gas is directly proportional to the absolute temperature (T):
(P
=
constant)
V
T
V=T or
-
=
constant
A
combination of the above two statements results in the equation of state termed
the
ideal
(or
perfect)
gas
law:
PM
or
p=-
RT
-
RT
PV=nRT or PV
=-
M
where n
is
m/M
=
number of moles of ideal gas, m
is
mass of gas present,
M
is
molecular weight of gas in mass per mole, V is
V/M
=
l/p
=
specific volume of ideal
gas in volume per mass, and
R
is universal gas constant in energy per mole per
absolute degree.
The values of
R
in different sets of units are given below:
8.314
8.314
82.057
83.14
62.36
21.85
10.73
0.7302
1545
1.987
1.987
Joules/g-mole
OK
m3 Pa/g-mole
OK
cm3 atm/g-mole
OK
cms bar/g-mole
OK
liter mm Hug-mole
OK
(ft)3(in.Hg)/lb-mole OR
ft3 atm/lb-mole OR
ft3 psi/lb-mole OR
(lb,/ftP)(fts)/lb-mole
OR
cal/g-mole
OK
Btu/lb-mole
OR
At atmospheric conditions, most ordinary gases such as air, nitrogen, etc., exhibit
P-V-T behavior that is well represented by the above equation. When n moles of an
ideal gas undergo a change of state, then
P,V,
=
nRT, and P,V,
=
nRT,

338
General Engineering and Science
or
where the subscripts
1
and
2
refer to the initial state and-final state, respectively.
It is a common practice to evaluate the molal volume
(
V) of an ideal gas at a set of
reference conditions known as the
standard
state. If the standard state is chosen to be
P
=
1
atm
=
760
mmHg
=
14.696
psia
and
T
=
0°C
=
273.16"K
=
32°F
=
491.69"R
Then
represents the volume occupied by
1
mole
of
any perfect gas, and has the following
values at the standard conditions of temperature and pressure (abbreviated as STP):
9
=
22.414
Q'g-mole
=
22,414.6
cm'/g-mole
=
359.046
ft'/lb-mole
The specific gravity
(G)
of
an
ideal gas relative to a reference gas (also assumed
ideal) is given by
It
simplifies to G
=
M/Mmf
when T
=
Tm,
and P
=
P,,,
Although real gases deviate from ideal gas behavior and therefore require different
equations of state, the deviations are relatively small under certain conditions. An
error Of
1%
or less should result if the ideal gas law were used for diatomic gases
when
V
2
5
llgm-mole
(80
ft'/lb-mole) and for other gases and light hydrocarbon
vapors whenV2
20
ygm-mole
(320
ft'/lb-mole)
[61,
p.
671.
Example
2-37
A
volatile compound of chlorine has been analyzed to contain
61.23%
of oxygen
(0,)
and
38.77%
of
chlorine (Cl,) by weight. At
1
atm and
27"C, 1000
cmJ of its vapor
weighs
7.44
g.
Assuming ideal gas behavior for the vapor, estimate its molecular
weight and deduce its molecular formula.
Solution
At
T
=
27°C
=
300.2"K
and
P
=
1
atrn,

Chemistry
339
7.44g
-
PM
1000cm'
RT
Mass density of the vapor
=
p
=
--
With
K
=
82.057 cm'-atm/g-mole
"K,
the molecular weight is calculated as
If
the unknown compound is made up of x atoms of chlorine and
y
atoms of oxygen,
its molecular formula
will
be
ClxOy.
Because the molecular weights of C1, and
0,
are
70.91 and 32.00 g/g-mole, respectively, we can express the weight composition
of
the
compound
as
weight of oxygen
-
(y)(32.00/2)
-
0.6123
weight
of
chlorine (x)(70.91/2) 0.3877
(given)
-
--
or
y
=
3.5~. Making this substitution in the formula for the molecular weight
of
the
substance, we have
70.91 32.00
189.3
=
M
=
(x)-
+(Y)2
2
or
2(
183.3)
=
70.91~
+
32(3.5)x
=
182.9~
:.
x
=
2(183.3)/(182.9) 2
With
x
=
2
and
y
=
7,
the compound has molecular formula CJO, with
M
=
182.9.
Mixtures
of
Ideal Gases
Two relations are postulated to describe the
P-V-T
behavior of ideal gas mixtures:
Dalton's Law
of
Partial Pressures.
The total pressure
(P)
of
a gaseous mixture
equals the sum
of
the partial pressures
of
its components.
By
definition, the
partial
pressure
of
any component gas
is
the hypothetical pressure it would exert
by
occupying
the entire volume
(V)
of the mixture at the same temperature
(T).
That is,
P
=
P,
+
P,
.l.
+
P,
=
Pi
where the partial pressure
of
component gas i in a N-component gas mixture is
n,RT
V
Pi
=
-
i
=
1,2,..-,N
by
the ideal gas law.
If
the mixture also behaves ideally, then

340
General Engineering and Science
Thus,
the
mole fraction
of
component gas i is
y,
=“i=fi,=
Partial pressure of i
’
n
P
Totalpressureofmixture
Amagat‘s
Law.
The total volume of a gaseous mixture equals the
sum
of the pure-
component volumes.
By
definition, the
pure-component
volume
of a component gas in
a mixture
is
the hypothetical volume that the component would occupy at the same
temperature and total pressure of the mixture.
By
Amagat’s law,
v
=
c
Vi
=
v,
+
v,
+
.
.
.
If each component gas as well as the mixture obeys the ideal gas law,
it
follows that
the pure-component volume of component
i
is
or
Thus, in an ideal gas mixture, the mole fraction of each component is identical
with its volume fraction (by Amagat’s law) or the ratio
of
its partial pressure to the
total pressure (by Dalton’s law). For both laws to be applicable simultaneously, the
mixture and its components must behave ideally.
The behavior of real gases is discussed in the previous section on “Thermodynamics
and Heat Transfer.”
Example
2-38
A
natural gas has the following composition by volume at
a
temperature of 80°F
and
a
gauge pressure of
40
psig-87.2% of methane, 4.5%
of
ethane,
3.6%
of propane,
1.8
%
of
n-butane, 1.0% of isobutane, and 1.9% of nitrogen. Assuming the ideal-gas
law is applicable, calculate (i) the average molecular weight of the mixture, (ii) density
of
the natural gas, (iii) specific gravity of the gas, (iv) volume occupied
by
100 Ib of
gas at
1
atm and
6OoF,
(v)
partial pressure
of
nitrogen, and (vi) purecomponent
volume of nitrogen per 1,000 ft$
of
gas.
Solution
Start with a
basis
of
1
Ib-mole of the natural gas at T
=
80°F
=
540”R and
P
=
40
psig
=
54.7
psia. The volume percent and mole percent compositions are identical
for a perfect-gas mixture.
(i)
The molecular weight
of
the gas mixture is
M
=
CyiMi
and
its
calculation
is
shown below in tabular form.

Chemistry
341
Component
i
MI
(IWlb-mole)
YI
m,
YlMl
(W
C2H6
30.07 0.045 1.353
CH4 16.04 0.872 13.987
C,H, 44.10 0.036 1.588
"'C4HTO
58.12
0.01
8 1.046
iso-C4H,, 58.12 0.01
0
0.581
N2
28.01
p.019
1
.ooo
:.M
=
mi
=
19.09 lb/lb-mole
(ii) With
R
=
10.73 ft5-psia/lb-mole
OR,
mass density of the mixture
Molar density c
=
p/M
=
0.180/19.09
=
9.44
x
gravity of the mixture is given by
Ib-moles/ft3
(iii) Assuming that air (reference substance) also obeys the ideal-gas law, the specific
p
-
M
-1909
G(80°F,54.7 psia)
=
-
-
-
-
-
=
0.659
P,,,
M~r
28.97
(iv)
At
TI
=
60°F
=
520"R and PI
=
1 atm
=
14.696 psia, the volume occupied by
n1
=
-
loo
lb-moles of the
gas
19.09
is
n,RT
-
-
(100)(10'73)(520)
=
1,988.3
ft.?
v,
=-
P, (19.09)( 14.696)
(v)
At
P
=
40 psig and
T
=
8OoF,
by Dalton's law of partial pressures,
P,
=
yip for
any component i in the mixture. Therefore, partial pressure of nitrogen
=
(0.019)(54.7)
=
1.039 psia.
(vi) Applying Amagat's law at the same conditions, the pure component volume
VI
=
y,V
for any
i.
For nitrogen,
V,
=
(0.019)( 1,000)
=
19.0 ft?.
Phase
Rule
and Phase Behavior
Gibb's
Phase
Rule.
The phase rule derived by
W.
J.
Gibbs applies to multiphase
equilibria in multicomponent systems, in the absence of chemical reactions. It is
written as
F=C?-6+2
where
5
is number of degrees of freedom
or
variance of the system,
C?
is minimum
number of independent chemical components in terms of which the composition of
each phase can be expressed, and
6
is
number
of
phases in the system.

342
General Engineering and Science
The term
5
denotes the number
of
independent phase variables that should be
specified in order to establish all
of
the intensive properties of each phase present.
The phase variables refer to the intensive properties of the system such as temperature
(T),
pressure
(P),
composition of the mixture (e.g., mole fractions,
T),
etc.
As
an
example, consider the triple point of water at which all three phases-ice, liquid water,
and water vapor-coexist in equilibrium. According to the phase rule,
5=e-p+2=1-3+2=0
The absence
of
any degrees of freedom implies that the triple point is
a
unique
state that represents an
invariant
system, Le., one in which any change in the state
variables
T
or
P
is bound to reduce the number
of
coexisting phases.
Phase Behavior
of
a Pure Substance
It is evident from the preceding example that a pure substance can have at
most three coexisting phases at equilibrium. At temperatures and pressures other
than the triple point, a pure substance may exist either as a single phase (e.g.,
solid, liquid,
or
vapor)
or
as a two-phase system. Application of the phase rule
for
6
=
1
gives
5
=
C?
-
6
+
2
=
1
-
1
+
2
=
2,
indicating that two intensive variables
(P
and
T) can be varied simultaneously in the single-phase region. On the other hand, in the
two-phase region
5
=
1
-
2
+
2
=
1
so
that either
P
or
T can be independently varied,
but not both for this monovariant system. Thus, the equilibrium phase behavior of a
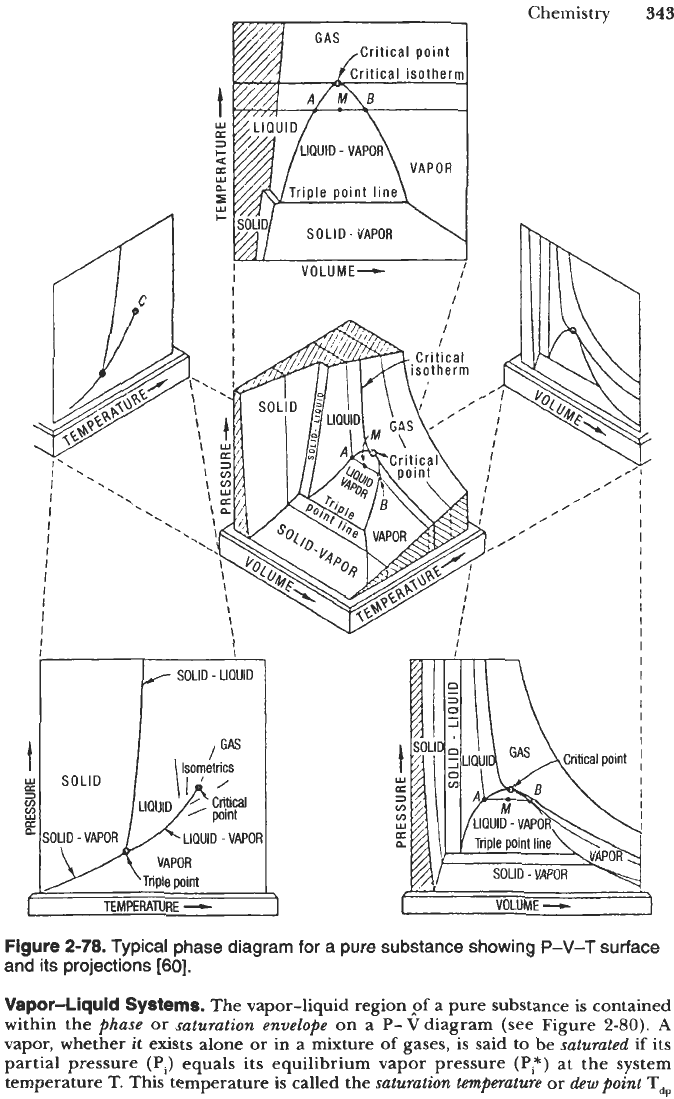
pure subspce is represented by a three-dimensional surface with pressure
(P).
specific
volume
(V),*
and temperature
(T)
as coordinates;
it
is called a phase diagram or
P-y-T
diagram (see Figure 2-78). Orthogonal projections of this surface onto the
P-
V
plane,
V
-T
plane, and
P-T
plane provide convenient means of depicting phase
phenomena ontwo-dimensional plots. Isotherms
(T
=
constant), isobars
(P
=
constant),
and isochors
(
V=
constant) are drawn as necessary
to
highlight important aspects of
phase behavior.
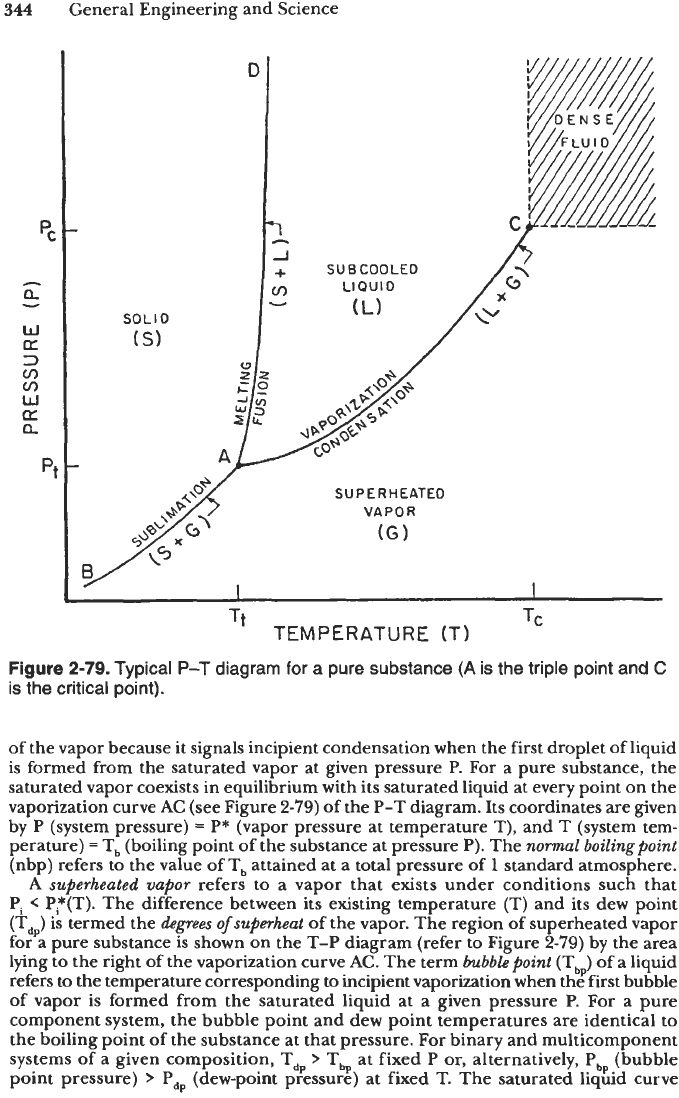
The
vapor pressure
(P*)
of a pure liquid at a given temperature (T) is the pressure
exerted by its vapor in equilibrium with the liquid phase in a closed system. All
liquids and solids exhibit unique vapor pressure-temperature curves. For instance,
in Figure 2-79, lines BA and AC represent the equilibrium vapor pressure curves of
the solid and liquid phases, respectively.
Phase transitions
refer to equilibrium processes involving a change of phase such as
sublimation (solid to vapor), boiling or vaporization (liquid to vapor), freezing (liquid
to solid), etc. On a
P-T
diagram (see Figure
2-79)
the phase transformations take
place on the sublimation curve BA, vaporization curve AC, and melting curve AD,
which separate the single-phase regions. Two phases coexist in equilibrium on each
of these phase-boundary curves, with the exception
of
the triple point,
A.
The
vaporization curve terminates at the critical point C of the pure substance at which
the distinction between liquid and vapor phases disappears and the latent heat of
vaporization becomes zero. The single phase that exists above the critical point
(Pc,
T,) is variously described as gas, dense fluid, or supercritical fluid. When
T
>
T,
it is
impossible to liquefy a dense fluid by varying the pressure alone.
Because a phase change is usually accompanied by a change in volume the two-
phase systems of a pure substance appear on a
P-
V
(or
a
T-
V
)
diagram
as
regions with
distinct boundaries. On a
P-
V
plot, the triple point appears as a horizontal line, and
the critical point becomes a point of inflection of the critical isotherm,
T
=
Tc (see
Figure 2-78 and Figure 2-80).
~~
~
~
*The intensive variable
for
volume
(V)
can be either the specific volume
(
$,
volume/mass)
or
the specific
molal volume
(
V
,
volume/mole).
I
J
SOLID
-
LIQUID
TEMPEWITURE
-
I
I
I
I
Figure
2-78.
Typical phase diagram
for
a pure substance showing
P-V-T
surface
and its projections
[60].
Vapor-Liquid
Systems.
The vapor-liquid
region
pf a pure substance is contained
within the
phase
or
saturation envelope
on a
P-
V
diagram (see Figure
2-80).
A
vapor, whether
it
exists alone
or
in a mixture
of
gases,
is
said
to
be
saturated
if
its
partial pressure
(Pi)
equals its equilibrium vapor pressure
(P?)
at the system
temperature T. This temperature
is
called the
saturation temperature
or
dew
point
T,
344
General Engineering and Science
pc
CI
a
w
3
v)
v)
W
a
Y
a
a
P
c
SOLID
(Sf
SUB
COOLED
LIQUID
(L)
SUPERHEATED
VAPOR
(G
1
9
#
1
I
TC
Tt
TEMPERATURE
(TI
Figure
2-79.
Typical
P-T
diagram for a pure substance
(A
is the triple point and
C
is the critical point).
of the vapor because it signals incipient condensation when the first droplet of liquid
is formed from the saturated vapor at given pressure
P.
For
a pure substance, the
saturated vapor coexists in equilibrium with its saturated liquid at every point on the
vaporization curve
AC
(see Figure
2-79)
of
the P-T diagram. Its coordinates are given
by P (system pressure)
=
P*
(vapor pressure at temperature T), and
T
(system tem-
perature)
=
T,
(boiling point of the substance at pressure
p).
The
normal boilingpoint
(nbp) refers to the value
of
Tb attained at a total pressure of
1
standard atmosphere.
A
superheated vapor
refers
to
a vapor that exists under conditions such that
Pi
<
P*(T). The difference between its existing temperature
(T)
and its dew point
(T,J is termed the
degrees ofsuperheat
of the vapor. The region of superheated vapor
for a pure substance is shown on the T-P diagram (refer to Figure
2-79)
by the area
lying to the right of the vaporization curve
AC.
The term
bubble point
(Tb) of a liquid
refers
to
the temperature corresponding to incipient vaporization when the fiist bubble
of vapor is formed from the saturated liquid at a given pressure P.
For
a pure
component system, the bubble point and dew point temperatures are identical to
the boiling point
of
the substance at that pressure. For binary and multicomponent
systems of
a
given composition, T,
Y
T at fixed P
or,
alternatively,
Pbp
(bubble
bp
point pressure)
Y
P, (dew-point pressure) at fixed
T.
The saturated liquid curve
