Ляско В.И. Стратегическое планирование развития предприятия

Подождите немного. Документ загружается.

гически, так и эмпирически,

путем

построения нескольких уравне-

ний

регрессии, отличающихся

друг

от

друга

по своей алгебраической

форме.

Сравнение их и выбор наиболее приемлемого для экономи-

ческого анализа уравнения производится статистически с помощью

коэффициента

множественной корреляции, коэффициента множест-

венной

детерминации и F-критерия (критерия Фишера).

Как

правило, процедура отбора факторов и построения уравнения

регрессии автоматизирована и осуществляется с помошью ПЭВМ

с использованием стандартного пакета прикладных программ.

Рассмотрим теперь применение многофакторных моделей для

прогнозирования воздействия некоторых факторов на такой пока-

затель, как прибыль предприятия. На основе динамики показателей

численности работающих на предприятии, объема выпускаемой

продукции, затрат на природоохранные мероприятия и количест-

ва автомобилей в предприятии несложно построить регрессион-

ную модель, позволяющую оценить значение прибыли. Опуская

математические расчеты, которые

следует

проводить на ПЭВМ по

специальным программам, для конкретных численных данных по-

лучаем

следующую

линейную многофакторную зависимость:

S = 3+O,O3 xN + 0,001 x

V-0,01

xZ + 0,001 xA,

где S —прибыль предприятия, млн руб.;

— численность работающих, чел.;

V — объем выпуска продукции, тыс. руб.;

— затраты на природоохранные мероприятия, тыс. руб.;

А — количество автомобилей, шт.

В последнем

году

численность работающих на предприятии со-

ставила 300 чел.; объем выпуска продукции — 50 млн руб.; затраты на

природоохранные мероприятия—600 тыс. руб.; количество автомоби-

лей —150 единиц. Подставив эти цифры в приведенную зависимость,

можно подсчитать размер прибыли предприятия в млн руб.

S = 3 + 0,03 х 300 + 0,001 х 50 - 0,01 х 600 + 0,001 х 150 = 6,2.

Анализ знаков коэффициентов при факторах в приведенной зави-

симости показывает, что все факторы увеличивают величину при-

были, за исключением затрат на природоохранные мероприятия.

131

Если прирост объема продукции составит

10%,

прирост работаю-

щих

— 5%, а

прирост автомобильного парка

—

10%,

то при

прежних

затратах

на

природоохранные мероприятия прибыль составит:

= 3 + 0,03 х (300 + 15) + 0,001х (50 + 5) - 0,01 х 600 + 0,001 х

(150 + 15) = 3 + 0,03 х 315 + 0,001 х 55 - 0,01 х 600

0,001 х 165 =

3 + 9,45 + 0,055 - 6 + 0,165 = 6,67.

Итак,

общая величина прибыли

— 6,67 млн руб., т.е. она

увели-

чилась

на 0,47 млн руб.

Наибольший вклад

увеличение прибыли

(0,45

) дал

прирост численности работающих.

5. Методы портфельного анализа (ПА)

ПА появился на основе обобщения и синтеза рекомендаций

ряда теоретических концепций, в частности концепции жизненно-

го цикла продукта

(ЖЦП).

Жизненный

цикл товара — это

концепция,

описывающая динами-

ку сбыта продукции, прибыли, потребителей, конкурентов и стра-

тегии маркетинга с момента поступления товара на рынок и до его

снятия

с рынка. Концепция жизненного цикла товара (продукта)

была предложена Теодором Левиттом в 1965 г.

Концепция

жизненного цикла продукта может применяться

отношении товарного класса, разновидности товара и торговой

марки.

Самый длительный жизненный цикл — у товарных классов,

а жизненный цикл марки товара зависит от ее

успеха

и от эффек-

тивности атак и контратак конкурентов.

Жизненный

цикл продукта — характеристика важная при опре-

делении товарной (продуктовой) политики фирмы как на текущий,

так и на перспективный момент ее развития. Важность и значи-

мость этой характеристики определяется тем обстоятельством,

что не только на разных рынках, но и на разных сегментах одного

того же рынка, продукт

(услуга)

находится на разных стадиях

цикла

спроса.

Хотя теоретическая кривая жизненного цикла спроса на про-

дукт

(услугу)

является более или менее одинаковой для большин-

ства продуктов

(услуг),

однако протяженность во времени и интен-

сивность перехода из одной стадии жизненного цикла в

другую

имеют большие различия в зависимости от специфических особен-

ностей каждого продукта (услуги).

Для любой фирмы (предприятия) это означает не только нерав-

номерность производственных затрат и неравномерность получе-

ния

доходов

в течение некоторого определенного периода време-

ни,

но и необходимость разработки для каждого продукта

(услуги)

своей стратегии поведения на рынке.

133

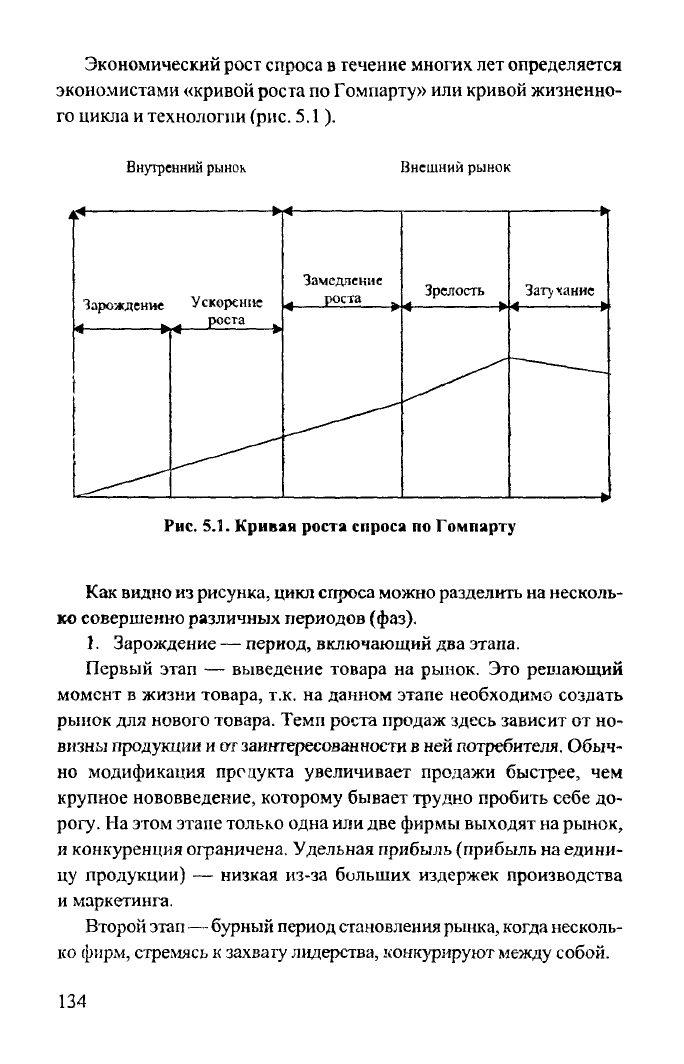
Экономический

рост спроса в течение многих лет определяется

экономистами

«кривой роста по

Гомпарту»

или кривой жизненно-

го цикла и технологии (рис. 5.1).

Внутренний рынок

Внешний рынок

Зарождение

* М

Ускорение

роста

Замедление

роста

Зрелость

Зату

хание

Рис.

5.1. Кривая роста спроса по Гомпарту

Как

видно из рисунка, цикл спроса можно разделить на несколь-

ко

совершенно различных периодов (фаз).

1. Зарождение — период, включающий два этапа.

Первый

этап — выведение товара на рынок. Это решающий

момент в жизни товара, т.к. на данном этапе необходимо создать

рынок

для нового товара. Темп роста продаж здесь зависит от но-

визны

продукции и от заинтересованности в ней потребителя. Обыч-

но

модификация продукта увеличивает продажи быстрее, чем

крупное нововведение, которому бывает

трудно

пробить себе до-

рогу.

На этом этапе только одна или две фирмы

выходят

на рынок,

конкуренция ограничена. Удельная прибыль (прибыль на едини-

цу продукции) — низкая из-за больших издержек производства

маркетинга.

Второй этап — бурный период становления рынка, когда несколь-

ко

фирм, стремясь к

захвагу

лидерства, конкурируют

между

собой.

134

2. Ускорение роста — период, когда конкуренты, оставшиеся

на

рынке, пожинают плоды своей победы. В этот период спрос

обычно растет, опережая предложение.

Еще несколько фирм проникают на рынок, увеличивая конку-

ренцию,

и отраслевой сбыт быстро увеличивается. Для соответ-

ствия

растущему

рынку предлагаются модифицированные вари-

анты базовой модели, относительная прибыль высока.

3. Замедление роста — проявляются первые признаки насыще-

ния

спроса, и предложение начинает опережать спрос.

4. Зрелость — спрос удовлетворен, и появились значительные

избыточные мощности.

В этот период товар имеет свой рынок и пользуется спросом.

В период зрелости конкуренция увеличивается и достигает своего

максимума, т.к. на рынок проникают многие фирмы. В

результате

сокращается прибыль в целом по отрасли и в расчете на единицу

продукции, поскольку распространяется система торговых ски-

док. Период зрелости отличается присутствием на рынке полной

ассортиментной группы товаров.

5. Затухание — период спада.

На

этой фазе товар, не претерпевающий никаких изменений,

надоедает потребителям, или же потребность, которую он был

призван

удовлетворить, исчезает. Непредсказуемой причиной

сокращения

объема продаж на этапе спада может стать техни-

ческое устаревание товара. Так, например, с появлением транзи-

сторов исчезли ламповые приемники. На фазе спада сокращается

сбыт в целом по отрасли, и многие фирмы

уходят

с рынка, по-

скольку сокращается число потребителей, а товарный ассорти-

мент концентрируется в моделях, обладающих наилучшим

спросом.

Таким

образом

затухание

— это период снижения объема

спроса (иногда до нуля), предопределяемое долговременными

демографическими и экономическими условиями (такими как

темп роста валового национального продукта или народонасе-

ления)

и темпом устаревания или уменьшения потребления про-

дукта.

135

точки зрения жизненного цикла спроса замедление роста

зре-

лость являются неизбежными последствиями экономического роста.

Продолжительность жизненного цикла отраслей сокращается

в ре-

зультате

прогрессивных новшеств

планировании

управлении,

повышении эффективности работы фирм, ускорении разработ-

ки

новой продукции, лучшей организации маркетинга

сбыта.

Таким

образом, если фирма заинтересована развиваться,

то ей

необходимо постоянно заботиться

диверсификации видов хозяйст-

венной

деятельности

отсекать

те,

которые больше

не

согласуют-

ся

ориентирами роста фирмы.

Эта

задача является ключевой

точки зрения управления стратегическим набором отраслей.

Другой,

не

менее важной задачей, является умение

предугадать

смену

фаз

цикла спроса

пересмотреть стратегию фирмы

соот-

ветствии

меняющимися условиями конкуренции.

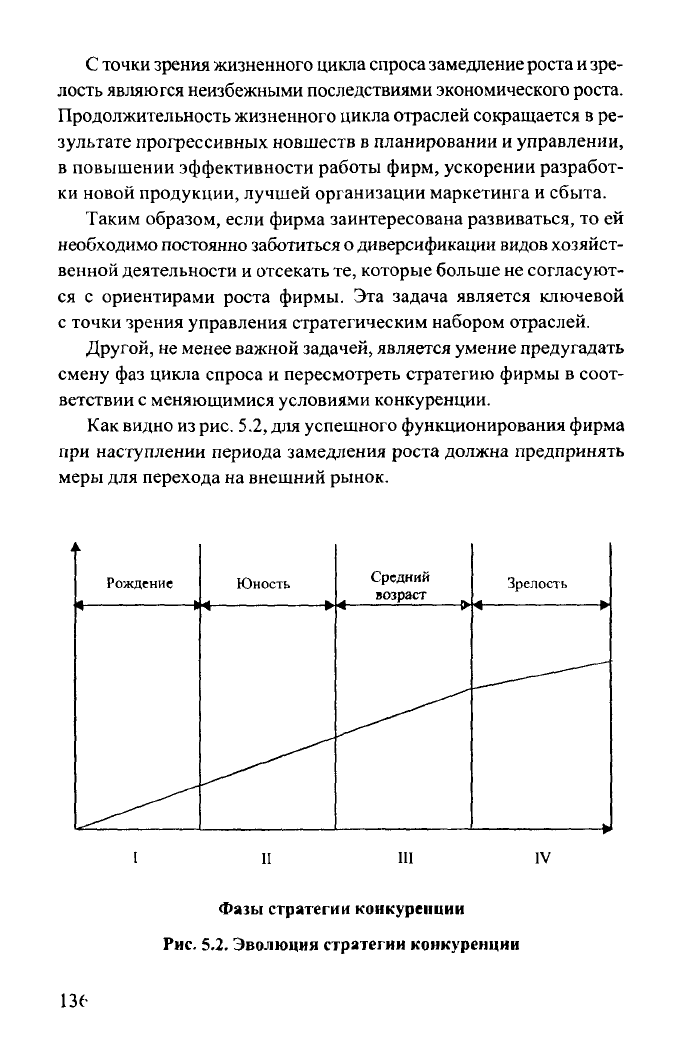
Как

видно

из

рис.

5.2, для

успешного функционирования фирма

при

наступлении периода замедления роста должна предпринять

меры

для

перехода

на

внешний рынок.

Рождение

Юность

Средний

возраст ^

Зрелость

III IV

Фазы

стратегии конкуренции

Рис.

S.2.

Эволюция стратегии конкуренции

Можно отметить также наличие факторов

успеха,

характерных

для той или иной фазы стратегии конкуренции:

' для 1-й фазы

—•

своевременно начатое освоение изделия (ус-

луги);

• для 2-ой фазы — реализация однородных изделий

(услуг)

по

самой низкой цене;

° для 3-й фазы — дифференциация товаров и рынков; предвиде-

ние

потребностей;

° для 4-й фазы — искусственное устаревание, обновление това-

ров,

сегментация рынков.

Основной

прием, применяемый в ПА, сводится к построению

матриц шахматного типа, в которых стратегии классифицируются

по

выбранным критериям. Каждой клетке, содержащей определен-

ный

вариант стратегии,

соответствует

пара количественных оце-

нок

двух

критериев.

Совокупный объем производимых фирмой (предприятием) то-

варов и

услуг,

реализуемый на рынках, формирует т.н. хозяйствен-

ный

портфель фирмы (предприятия). Все

услуги,

оказываемые

фирмой,

и все товары, выпускаемые фирмой, называются содержи-

мым хозяйственного портфеля фирмы.

В самом общем смысле под портфелем понимается пакет цен-

ных

бумаг,

принадлежащих какому-либо лицу (фирме) — это наи-

более распространенное значение понятия «портфель», употреб-

ляемое по отношению к бизнесу. В расширенном толковании это

понятие

также используется для обозначения какой-либо группы

хозяйственных подразделений, принадлежащих одному и

тому

же

владельцу.

Портфель фирмы (предприятия) в соответствии с наименовани-

ем выпускаемых товаров одной или нескольких ассортиментных

групп или видов работ на определенный рынок (или его сегмент),

разбивается на подразделения. Такие подразделения фирмы (пред-

приятия)

называются стратегическими хозяйственными подразде-

лениями

(СХП).

Стратегическое хозяйственное подразделение (СХП) является

основной,

первичной ячейкой предприятия (фирмы), для которой

137

вырабатывается деловая стратегия. Это обособленная часть биз-

неса, отвечающая за определенный вид деятельности предприятия

(фирмы).

Сочетание СХП в портфеле фирмы (предприятия) и направле-

ния

их развития определяются стратегией развития хозяйственно-

го портфеля фирмы (предприятия).

Рыночная

ситуация определенным образом влияет на формиро-

вание стратегических хозяйственных подразделений, определяю-

щих развитие хозяйственного портфеля фирмы.

Среди разнообразия методов портфельного анализа наи-

большее распространение получили методы, приведенные

табл. 5.1.

Таблица

5 1

Методы

ПА

Me год, предложенный

Бостон

консалтинг групп

—

матрица «портфеля продукции»

Метод, предложенный

фирмой

«Артур Д

Литтл»

—

матрица «жизненного

цикла»

Метод, предложенный фирмами

«Шел», «Дженерал

Фудз»

—

матрица «направлений хозяйствен-

ной

деятельности»

Метод, предложенный Стен-

фордским исследовательским инс-

титутом,

—

матрица «отраслевой

дифференции»

Метод, предложенный «Интср-

нейшнл

харвестер

компани»,

—

матрица «стратегического разви-

тия»

Критерии

классификации

1) рост рынка

2) размер доли рынка

1) конкурентная позиция

2) технологическая позиция

1) конкурентоспособность

2) привлекательность рынка

1) возможность дифферен-

циации

2) высота барьеров

доступа

отрасли

1) объем продаж

2) рост рынка

3) прибыльность

4) размер доли рынка

138

5.1.

Метод «Бостон консалтинг

групп»

(БКГ),

или

модель «Доля рынка — рост рынка»

Концепция

ЖЦП легла в основу разработки указанного метода,

являющегося одним из методов ПА — матрицы «портфеля продук-

ции» корпорации, предложенного консультационной фирмой «Бос-

тон

консалтинг групп». Этот метод предполагает оценку возмож-

ностей

корпорации по

двум

критериям:

1) рост рынка, измеряемый по абсолютному объему отрасле-

вых продаж и темпам его роста;

2) размер контролируемой корпорацией доли рынка, измеряе-

мый

в процентах, и общеотраслевого объема продаж.

В соответствии с этим методом все поле деятельности предпри-

ятия

представляется как совокупность «стратегических хозяй-

ственных подразделений» (СХП), составляющих хозяйственный

«портфель» предприятия. СХП — это независимые

друг

от

друга

сферы

деятельности предприятия, которые характеризуются

определенным продуктом (или их группой), кругом клиентов

особыми рыночными задачами. Каждое СХП имеет свои цели,

рыночные

возможности и риски. Каждое СХП может быть описа-

но

рядом показателей:

1) объемом рынка СХП, равным сумме объемов реализации про-

дуктов всеми производителями;

2) долей предприятия в объеме рынка СХП;

3) стадией ЖЦП СХП (рыночное развертывание, рост и т д);

4) конкурентной позицией предприятия (сильная, слабая, средняя).

В каждый временной период предприятие имеет конкретный

набор

СХП, который подлежит анализу и оценке в целях его опти-

мизации.

Необходимость систематического пересмотра портфеля СХП

обусловлена

изменениями,

происходящими во внешней и внутрен-

ней

среде предприятия. Стратегическое положение СХП опреде-

ляется с помощью двухкоординатной матрицы, состоящей из четы-

рех полей. Матрица образована характеристиками

«доля

рынка»

«рост

рынка».

139

Построение

матрицы основано на следующих предпосылках:

• объем доходов корпорации прямо пропорционален величине

ее рыночной доли;

• наращивание объемов производства

требует

финансовых вло-

жений,

потребность в которых прямо пропорциональна темпам

роста рынка,

• замедление темпов роста рынка при сохранении сильных ры-

ночных позиций создает возможность получения избыточных

доходов;

• сокращение рыночной доли на стагнирующем рынке приводит

росту доходов.

В соответствии с этими положениями выделяют четыре катего-

рии

продукции в стратегических хозяйственных подразделениях

соответствующие им типы стратегий.

СХП

«Звезда».

Данное СХП

дает

большой

доход,

но

требует

значительных вложений. Для такого СХП характерны высокие

темпы роста и большая доля рынка.

Высокая доля фирмы в быстрорастущей отрасли

(рынке),

а также

лидирующее положение, которое она занимает на рынке, принося

значительные доходы, однако большую их часть фирма вынуждена

трагить на поддержание своего отличительного преимущества —

лидирующего положения. Отсюда данное СХП постоянно испыты-

вает недостаток средств. Основная стратегия корпорации — это

проникновение

на новые рынки и (или) формирование новых сег-

ментов на существующих рынках, освоение новых каналов систе-

мы

распределения. При ориентации на это СХП расходы фирмы на

рекламу и совершенствование продукта остаются на высоком

уровне.

2. СХП «Дойная корова». Это СХП

дает

большой

доход

и харак-

теризуется малыми затратами в связи со стабильностью рынка, на

котором функционирует фирма. Для СХП характерны низкие тем-

пы

роста рынка и большая доля рынка.

Высокая доля стабилизирующейся или стареющей отрасли

(рынка),

на которой фирма занимает лидирующее положение,

приводит к устойчивым и достаточно высоким для нее прибылям.

140