Лукашевич М.Г. Введение в магнитоэлектронику
Подождите немного. Документ загружается.


1
]22/5([
)2/5()32/5(
2
−
+
+
+
=
rГ
rГrГ
b
r
(17)
Величина коэффициента магнитосопротивления и показатели
степени зависмости времени релаксации импульса от энергии для
основных механизмов рассеяния приведена в таблице №1. Как видно из
таблицы максимальная величина коэффициента магнитосопротивления
характерна для рассеяния носителей на ионах примеси и для всех
механизмов рассеяния он меньше единицы. Необходимо отметить, что
если образец не слишком однороден, то b
r
может достигать величин
больших единицы, однако рассмотрение магниторезистивного эффекта в
таких образцах существенно усложняется.
Таблица 1.
Показатель степени и коэффициент магнитосопротивления для разных механизмов
рассеяния носителей заряда
.
№ п/п Механизм рассеяния
r b
r
№1 Акустический деформационный потенциал 1/2
0,274
№2 Ионизированные примеси 3/2 0,578
№3 Рассеяние на нейтральных примесях 0 0
№4 Акустический пьезоэлектрический потенциал -1/2 0,087
№5 Рассеяние на дислокациях 1/2 0,274
Как видно из формулы (17) характерной особенностью
лоренцевского магниторезистивного эффекта является зависмость его
величины от показателя степени в зависимости времени релаксации
импульса от энергии. Следовательно, если в кристалле имеется
несколько видов носителей заряда хотя и одного знака, то следует
ожидать существенного увеличения магниторезистивного эффекта.
Формулы для расчета магнитосопротивления в этом случае
усложняются. Так в случае двухзонной проводимости носителями
одного знака магниторезистивный эффект можно рассчитать по формуле
⎭
⎬
⎫
⎩
⎨
⎧
+
+
+
+
+
=
Δ
21
221
2|
1
2
21
2|
21
2
2
0
)(
)(
)1(
)(
nbn
bnbbbn
nbn
bbnn
B
R
R
rr
H
μ
, (18)
где первый член в правой части (18) обусловлен смешанным механизмом
проводимости и исчезает при n
1
=0 или n
2
=0, а второй член описывает
магнитосопротивление каждого типа носителей заряда в отдельности.
Коэффициенты
2
1
μ
μ
=b
и
2
1
|
H
H
b
μ
μ
=
представляют собой отношение
11

дрейфовых и холловских подвижностей первого и второго типов
носителей заряда. Выражение (18) легко модифицируется для случая
смешанной электронной и дырочной проводимости полупроводника.
2. ЛОРЕНЦЕВСКИЙ МАГНИТОРЕЗИСТИВНЫЙ ЭФФЕКТ В
КВАНТОВОМ ПРЕДЕЛЕ
Квантовомеханическое рассмотрение движения электрона в
магнитном поле показывает, что круговое движение в плоскости,
перпендикулярной полю, квантуется, а энергетический спектр при этом
становится дискретным. Для полупроводников у которых закон
дисперсии является квадратичным и поверхности постоянной энергии
представляют собой эллипсоиды вращения, трехмерная разрешенная
зона распадается на две подзоны, соответствующие противоположным
направлениям спина. Энергия носителя в зоне с учетом спина имеет вид
gВmn
m
k
Bsc
z
μωε
+++= )2/1(
2
*
22
h
h
, (19)
где n – осцилляторное квантовое число, m
s
=±1/2, μ
В
– магнетон Бора, -
постоянная Планка, g – фактор спектроскопического расщепления, k
h
z
–
компонента волнового вектора в направлении магнитного поля.
Энергетические уровни (или подзоны) в плоскости перпендикулярной
магнитному полю называются уровнями (подзонами) Ландау. В сильном
магнитном поле расстояние между двумя уровнями Ландау становится
больше их теплового размытия
Tk
Вс
>
ω
h
, (20)
где Т – абсолютная температура, k
B
– постоянная Больцмана.
Удовлетворяющие (20) магнитные поля называют квантующими. Из
условий (12) и (20) видно, что критерий сильного в классическом смысле
и тем более квантующего магнитного поля легко выполняется при
низких температурах для полупроводников с малой эффективной массой
и высокой подвижностью носителей заряда. Если в магнитном поле
уровень Ландау с n=0 пересекает энергию Ферми ε
F
для электронов в
кристалле, то такой предел по “силе” магнитного поля называют
ультраквантовым. Условное деление магнитного поля, по влиянию на
заряженную частицу в кристалле показано на рис. 2
12

Квантование энергетических уровней в сильном магнитном поле
приводит к существенному изменению и вида плотности разрешенных
состояний как функции энергии. Для плотности состояния g(ε) в
магнитном поле можно записать
∑
=
−
++−=
max
0
2/1
32
2/3*
])2/1([
2
2
)(
n
n
Bsc
c
gBmn
m
g
μωε
ω
π
ε
h
h
h
(21)
Из (21) видно, что g(ε) обращается в бесконечность у дна каждой
подзоны Ландау и спадает как ε
-1/2
, оставаясь пропорциональной
магнитному полю при удалении от нее. Иллюстрация изменения зонной
структуры и плотности состояний в магнитном поле приведена на рис. 3.
Квантование энергетического спектра носителей заряда приводит к
тому, что в квантующем магнитном поле вероятность перехода
электрона из одного состояния в другое начинает зависеть от величины
магнитного поля. Проведенный квантовомеханический рассчет
магниторезистивного эффекта показал, что в этом случае наблюдается
увеличение сопротивления как в скрещенных, так и в параллельных
электрическом и магнитном полях. При этом магнитосопротивление
степенным образом зависит от напряженности магнитного поля и
температуры.
ηα
TB
R
R
∝
Δ
0
(22)
Рис.2. Условная шкала деления магнитного поля.
13
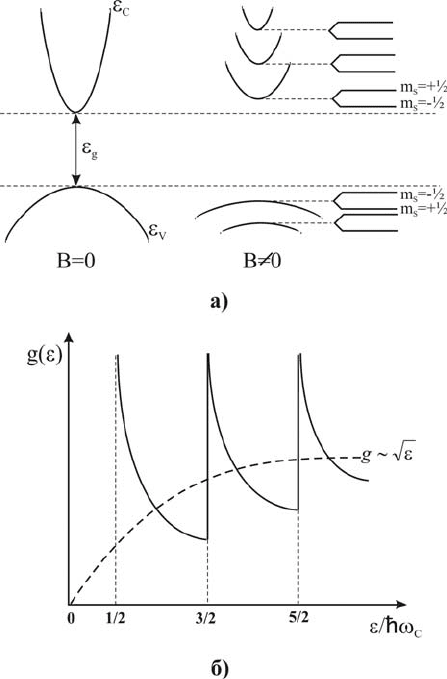
Рис.3. Изменение зонной структуры полупроводника (а) и плотности
состояний (б) в квантующем магнитном поле.
Так же как и в слабом магнитном поле магниторезистивный
эффект в квантовом пределе положителен, т.е. сопротивление в
14
магнитном поле увеличивается, однако в этом случае вид
магнитополевой зависимости определяется механизмом рассеяния
носителей заряда, в то время как в классических полях он определяет
величину эффекта при параболической зависимости от поля. Показатели
степени для не вырожденных и вырожденных полупроводников и разных
механизмов рассеяния носителей заряда приведены в таблице 2. Можно
отметить, что сравнение расчетов МС в области классически сильных
магнитных полей на основе кинетического уравнения с
квантовомеханическими показало на их совпадение.
Таблица 2
Показатели степени магнитополевой и температурной зависимости магниторезистивного эффекта в
квантовом пределе
Невырожд. полупроводн сильно выр. полупроводн
Механизм рассеяния
α⊥
α||
η⊥
η||
α⊥
α||
η⊥
η||
Акустические фононы (низкие
темп.)
5/2 -3/2 3/2 -1/2 11/2 0 5/2 0
Акустические фононы
(высокие темп.)
2 -1/2 1 1/2 5 1 2 1
Точечные дефекты 2
-3/2 1 -1/2 5 0 2 0
Пьезоэлектрический (низкие
темп.)
3/2 -3/2 1/2 -1/2 9/2 0 3/2 0
Пьезоэлектрический (высокие
темп.)
1 -1/2 0 1/2 4 1 1 1
Оптические фононы (высокие
темп)
1 -1/2 0 1/2 4 1 1 1
Ионизированные примеси 0 -3/2 0 -3/2 3 0 3 1
Схематическое изображение магнитополевых зависимостей
лоренцевского магниторезистивного эффекта в области классических и
квантующих
магнитных полей показано на рис. 4.
15
(α = 0 - 11/2)
~H
α
const
const
~B
2
ћω
C
=ε
F
ћω
C
=k
B
T
μB=1
ΔR/R
0
В
Рис. 4. Схематическое представление магниторезистивного эффекта при
зонном механизме проводимости в классических и квантующих
магнитных полях.
3. РАЗМЕРНЫЙ ЭФФЕКТ В ЛОРЕНЦЕВСКОМ
МАГНИТОСОПРОТИВЛЕНИИ
Как отмечалось ранее при рассмотрении магниторезистивного
эффекта на основе кинетического уравнения Больцмана, величина
измеряемого магнитосопротивления ограниченного образца зависит не
только от напряженности магнитного поля, но и от размеров и формы
образца. Для простейших форм, например для прямоугольного
параллелепипеда, выполнены детальные расчеты, связывающие
величину магнитосопротивления с соотношением длины l образца к его
ширине b (u=l/b). В отдельных частных случаях можно выписать
следующие явные зависимости магнитосопротивления от напряженности
магнитного поля и отношения длины образца к ширине:
),(),(/),(/
00
β
β
ρ
ρ
β
ρ
ρ
ugu
∞
Δ
=
Δ , (23)
16

где
()
⎪
⎩
⎪
⎨
⎧
+
+=
,1
,1
,1
),(
2
2
β
ββ
ug
0
1
=
=
∞=
u
u
u
Графики функций g(β) при разных u приведены на рис.5.
Предельный случай u=0 (неограниченный, бесконечно широкий образец)
можно реализовать на практике, взяв круглый диск с одним электродом в
центре и другим на периферической окружности (так называемый диск
Корбино, рис. 6, а). Электрическое поле в этом случае имеет лишь
радиальную составляющую, а линии тока – вид логарифмических
спиралей, которые пересекают радиусы диска под углом Холла. Другой
предельный случай u=∞ можно реализовать, взяв длинный тонкий
стержень (рис.6, б.). Понятно, что физический магниторезистивный
эффект, в котором коэффициент магнитосопротивления характеризует
механизм взаимодействия носителей заряда с кристаллической
решеткой, можно измерить на длинном тонком стержне, когда
геометрической компонентой магнитосопротивления можно пренебречь.
Если время релаксации не зависит от энергии т.е. показатель
степени r в формуле (16) равен нулю, то величину
магнитосопротивления прямоугольного параллелепипеда в широком
интервале напряженности магнитного поля и отношений l/b можно
определить из следующей формулы
1
)11)((1
)]11)((1[1
2
22
0
−
−++
−+++
=
Δ
β
ββ
ρ
ρ
uf
uf
, (24)
где
u
uG
uf
−
−
=
1
1)(2
)(
,
а
∑
∞
=
+
+
=
0
3
2
)12(
12
1116
)(
k
Ukth
kU
uG
π
π
-
функция Курта-Липмана. График зависимости величины G от отношения
длины образца к его ширине приведен на рис.7.
Если время релаксации импульса зависит от энергии, т.е. r≠0, в
выражении (24) β необходимо заменить на β
*
μ
μ
ββ
В
2
*
=→
. (25)
17
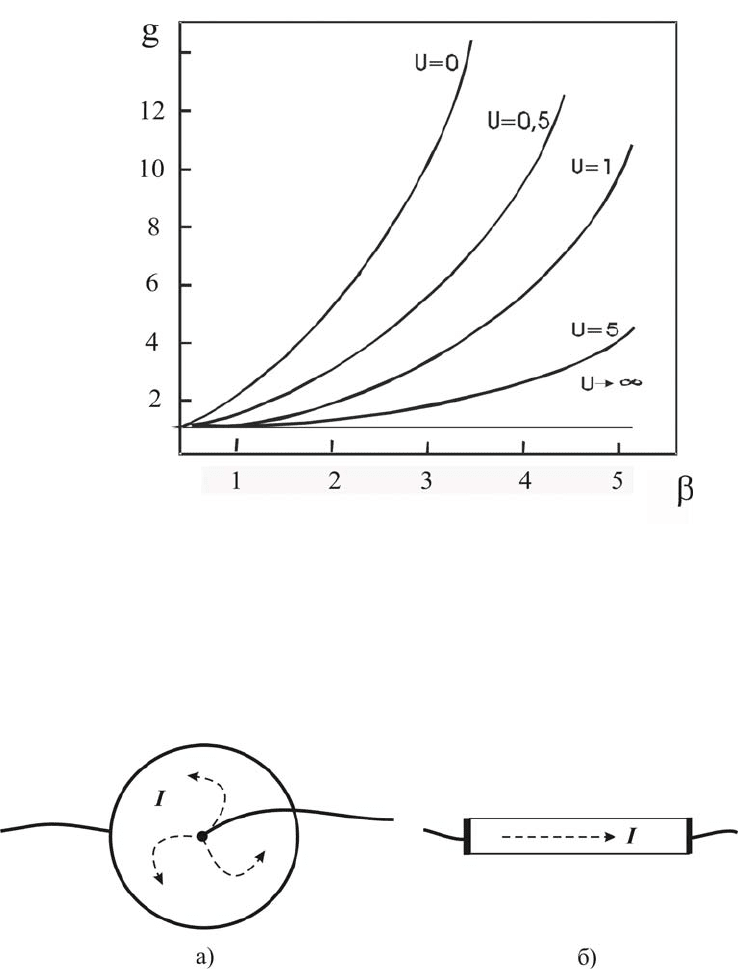
Рис.5. Зависимость геометрического множителя от β при разных
значениях u.
Рис.6. а) диск Корбино; б) длинный тонкий стержень.
18
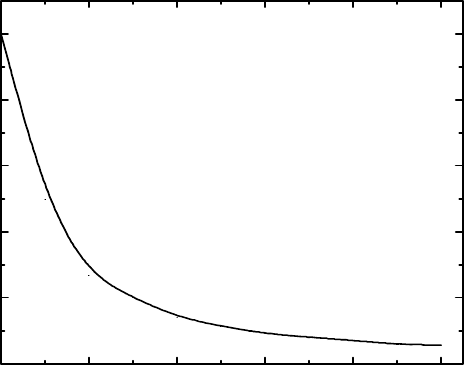
0246810
0,0
0,2
0,4
0,6
0,8
1,0
G
u
Рис. 7. Зависимость геометрического множителя Курта-Липпмана от
отношения длины образца к его ширине u=l/b.
4. МАГНИТОРЕЗИСТИВНЫЙ ЭФФЕКТ В ОБЛАСТИ
ПРЫЖКОВОЙ ПРОВОДИМОСТИ
При высоких температурах полупроводниковые материалы
обладают собственной электропроводностью, связанной с
температурным забросом электронов из валентной зоны в зону
проводимости. Так как ширина запрещенной зоны у их достаточно
велика , то при понижении температуры концентрация свободных
носителей в зоне проводимости быстро убывает, пока их не станет
меньше, чем носителей, поставляемых в зону проводимости примесными
атомами. Дальнейшее понижение приводит к постепенному
“вымораживанию” примесных электронов, т.е. возвращению электронов
на доноры. Постепенное вымораживание электронов на доноры при
понижении температуры должно приводить к тому, что сопротивление
полупроводникового кристалла стремится к бесконечности. Однако
сопротивление кристалла не становится равным бесконечности, так как
его электропроводность начинает определяться прыжками электронов
непосредственно по донорам, без активации в зону. Такой механизм
проводимости называют прыжковым. При этом электрон прыгает с
19

занятого донора на свободный и, следовательно, необходимым условием
прыжковой проводимости является наличие свободных мест на донорах,
т.е. компенсации полупроводникового материала. Температурная
зависимость при этом может быть аппроксимирована формулой
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
TkTk
T
BB
3
3
1
1
expexp)(
ε
ρ
ε
ρρ
(26)
с соответствующими энергиями активации ε
1
– энергия ионизации
донорного уровня и ε
3
– энергия активации прыжковой проводимости по
донорным уровням.
На рис. 8 схематически изображена зависимость логарифма
сопротивления слабо легированного полупроводника от обратной
температуры. Область 1 соответствует собственной проводимости, а
области 2-4 соответствуют примесной проводимости.
Прыжковому механизму проводимости соответствует очень малая
подвижность, так как прыжки электронов связаны со слабым
перекрытием хвостов волновых функций соседних центров. Несмотря на
это, прыжковый механизм проводимости дает больший вклад, чем
зонный, так как число прыгающих электронов значительно больше числа
свободных электронов в зоне проводимости.
4
3
2
1
Ln R
T
-1
Рис. 8. Схематическая температурная зависимость сопротивления слабо
легированного полупроводника: 1 - область собственной
проводимости, 2 - область истощения примеси, 3 - область
вымораживания носителей на примесь, 4 - область прыжковой
проводимости.
20
